尺度效应——大小各有优势

涂 泓(上海师范大学数理学院物理系 上海 200234)

尺度效应
——大小各有优势

涂 泓
(上海师范大学数理学院物理系 上海 200234)

尺度表征物体的大小，尺度效应则反映出一个物体的大小决定了它的许多物理特性.用量纲分析的方法，加上一些简单的计算，解释了各种物理量对尺度的依赖关系，并在此基础上介绍生活中各种各样的尺度效应.

尺度 特征长度 能量 比例

物体最明显的特征就是它们的大小，而不同大小的物体也有着其明显不同的物理特征.事实上，这种联系并不像我们想象的那么简单，而是有着深层原因的.物体的许多物理性质、表观现象，都是因其大小而产生的效应.

1 尺度及其表示

“尺度”通常指物体的大小，而且是用来区分大小不同而形状却一样的物体的.以长方体为例，一个长方体的大小与其长、宽、高3个参数都有关，其体积等于三者的乘积.但对于形状一样的物体而言，长、宽、高之间的比例必须保持不变，这时候，只需要一个参数就完全决定了长方体的大小.比如，某个形状一定的长方体，它的长度a，宽度b和高度c之间满足确定的比例关系，可以写成b=k1a，c=k2a，其中k1和k2为确定该长方体特定形状的两个常数，则体积V=abc=k1k2a3，可见，仅一个长度参数a就决定了该长方体的大小.通常把这个决定物体大小的唯一参数称作“特征长度”，或者说，一个物体的尺度可以用它的“特征长度”来表示.

实际上，一个形状一定的长方体的长、宽、高三者中的任意一个都可以选作它的特征长度.同样，对于一个形状一定的圆柱体而言，它的柱体长度和横截面半径之间的比例是确定不变的，所以长度和半径两者中的任意一个也都可以作为圆柱体的特征长度.一个球体的特征长度自然就是它的半径了.其实，对于任何形状的物体，总可以用一个特征长度来表征它的大小.

2 尺度和物理量

物体的许多物理量都与它的尺度密切相关，其中最基本的就是物体的体积、表面积和截面积.以L表示物体的特征长度，则物体的体积V与L的三次方成正比，即V∝L3.物体的表面积S与L的二次方成正比，即S∝L2，同样，物体的横截面积也是与L的二次方成正比的.

另外，由于物体的很多特性都直接或间接地与其体积、表面积或截面积相关，所以也就与其自身的尺度有着密切的关系了.比如，对于一个质量分布均匀的物体，因其密度为恒量，所以物体的质量M正比于体积，也与尺度L的三次方成正比，即M∝L3.又如，潮湿物体水分蒸发的快慢一般与其表面积的大小成正比，所以在其他条件不变的情况下，物体在单位时间内蒸发掉的水分量m与其尺度L的二次方成正比，即m∝L2.还有一个简单的例子就是电阻.以相同材料做成的形状相似而大小不同的圆柱形均匀电阻为例，由于电阻值与长度成正比，而与截面积成反比，所以阻值的大小R与其尺度L的一次方成反比，即R∝L-1，也就是说，圆柱形尺度越大，其阻值反而越小.

正是由于尺度差别不仅仅是大小比例的简单缩放，而是影响到物体的方方面面，因此尺度效应可以说是无处不在.有些时候，我们明显能发现物体的大小决定了它在某些方面占优势，在另一些方面却处于劣势，可谓“尺有所短，寸有所长”.

3 尺度效应——大有大的优势

(1)大型动物耐饥、耐寒能力强、寿命长

动物体内的热量在不断地通过身体表面排放出去，同时摄入的食物又在不断转化成能量，恒温动物通过维持输入和输出能量两者之间的平衡而保持恒定的体温.

热量通过动物表面释放出去，从而与它的特征长度L的平方成正比，这就意味着动物的散热率和产热率(即新陈代谢率)P应该满足

(1)

(2)

为了计算方便，我们将式(1)写成等式的形式

P=CMα

(3)

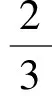
logP=αlogM+logC

(4)

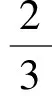
由于维持新陈代谢所需的能量来自食物摄入，因此式(2)相当于告诉我们

(5)

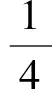
(6)

由于新陈代谢率高，因此小型动物常常因为得不到足够的食物而面临体温过低的问题.此外，由于体型的限制，它每次吃不下很多食物，而是正比于它的体重M，于是它就不得不增加进食次数.许多大型动物一天只需要吃一顿，而小动物的生活却是在不断地觅食、进食中度过的.比如说有一种叫做鼩鼱的小动物，只要三小时找不到食物吃就会饿死.

事实上，小动物每天由摄入食物所获得的能量，大部分都用于维持体温.相比之下，大型动物更容易维持体温，甚至常常因为体表来不及散发足够的热量而导致体温过高.而这就是为什么寒冷地区以北极熊、海象、海豹这样大型动物为主.

正因为式(2)告诉我们，越小的动物新陈代谢活跃性越高，因此小型哺乳动物呼吸频率都很快，以获得自己所需要的氧气，而氧气需要依靠血液传输，这又需要心脏跳动泵血，因而小动物心跳也很快，由此尺寸最终决定了动物的寿命.例如，大象大约每分钟呼吸6次，心跳30次，寿命40年；而老鼠大约每分钟呼吸150次，心跳600次，寿命3年.经过简单计算，我们会惊奇地发现，它们一生中总的呼吸次数和心跳次数都大致相同.

(2)小虫怕水

昆虫不惧怕重力，它不但能毫无危险地从高处落下来，还能不费吹灰之力就附着在墙壁上或天花板上.不过，有一种力对于昆虫而言，就如同重力对于大型动物一样可怕，那就是表面张力.一个物体从液体中出来时，由于表面张力而携带一薄层液体.假设这是一个半径为r，质量为M的球形物体，它所携带的水膜厚度为d，那么此时这些液体总质量占该物体本身质量的比例为

(7)

(3)大型哺乳动物潜水时间长

(8)

抹香鲸的潜水时间为一个半小时左右，如此长的潜水时间，跟它的庞大体型是分不开的.一条中等抹香鲸的体重大约20 t，按照式(8)折合成一个体重60 kg的人，那么这个人的潜水时间应该是12.98 min，而2015年的吉尼斯世界纪录为18.06 min！

4 尺度效应——小有小的好处

(1)小虫不怕摔

(9)

从而得到

(10)

我们假设这个物体是一个半径为r，密度为ρ物的球体，那么

(11)

举例来说，小水滴的直径约1 mm，因此其下落的终极速率为

(12)

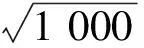
(2)小动物爬高更轻松

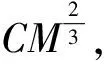
(13)

(3)细胞长不大

不同的生物体特征尺度从几纳米到数十米，其间可相差十个数量级，但构成它们的细胞直径却大多在10～100 μm范围内.当细胞长大到一定程度时，它们就开始分裂，仿佛有什么因素限制了它们的尺寸.而这个限制因素，就是细胞作为代谢基本单位的主要功能之一——与外界交换物质与能量.要维持细胞的正常代谢，就要保证有稳定的物质与能量通过细胞膜进出细胞.以能量为例，假设细胞体积为V，面积为S，单位时间经过单位面积细胞膜的能量(即能流)为Q，那么为了保持动态平衡，在Δt时间内通过细胞膜进入细胞的总能量

W=QSΔt

(14)

应该等于细胞内消耗的总能量

W=ωVΔt

(15)

其中ω为细胞内单位体积所消耗的能量，细胞正常运作时这个值应该保持不变.表面光滑的细胞满足前文所说的V∝L3、S∝L2的关系，于是我们从式(14)、(15)不难得出

(16)

也就是说，当细胞直径L增大为原来的10倍时，单位时间经过细胞膜单位面积的能量Q也要增大为原来的10倍.同理，此时单位时间经过细胞膜单位面积进入细胞的氧气量也是原来的10倍，单位时间经过细胞膜单位面积排出细胞的废物也是原来的10倍.而细胞膜的生物性质决定了这些值都存在着一定的上限.细胞为了维持最佳的能量、物质输运，就必需限制其体积的大小.

从以上分析也可以看出，当细胞不需要与外界交换物质、能量时，就不会受到这些限制.这就是卵细胞可以长到很大的原因.世界上最大的细胞是鸵鸟蛋，直径可达15～22 cm.另一方面，有些细胞需要与外界发生大量的物质和信息交换，如神经元.它们的表面具有许多突起，这样就在不增大体积的前提下增大了相对表面积.

5 结束语

从本文的分析可见，尺度效应是可以从理论上预见到的，而事实也很好地验证了这些理论预言.从尺度的视角去分析看待这个世界，其中大大小小都显得合情合理.

1 Knut Schmidt-Nielsen. Scaling. Cambridge University Press, 1984

2 J. B. S. Haldane. On Being the Right Size. Oxford University Press, 1985

3 J. Maynard Smith. Mathematical Ideas in Biology. Cambridge University Press, 1968

4 T. W. Körner. The Pleasure of Counting. Cambridge University Press, 2011

2017-02-22)