求圆周角常见错误分析

张静

求圆周角常见错误分析

张静

圆是初中阶段重要的知识点，是中考考查重点内容之一.同学们在学习过程中感到知识点特别多，理解起来又特别难.针对弧、弦、圆心角与圆周角之间的联系，特别在求圆周角时常会出现错解、漏解等情况，借此文，笔者把求圆周角的易错之处总结并归纳.

类型一：知弦求圆周角

例1在直径为10cm的⊙O中，弦AB=5cm，则弦AB所对的圆周角为_______.

【错解】30°.

【错解原因】在同圆中，一条弦对着无数个圆周角，在这无数个圆周角中又可分为两种情况，一种是圆周角的顶点在优弧上，另一种是在劣弧上.同学们在无具体图形情况下，会习惯性地画出弦AB向上所对的圆周角这一种情况，其实还有向下所对的圆周角，且这两种情况的圆周角构成一个圆内接四边形，即对角成互补关系，如图1.

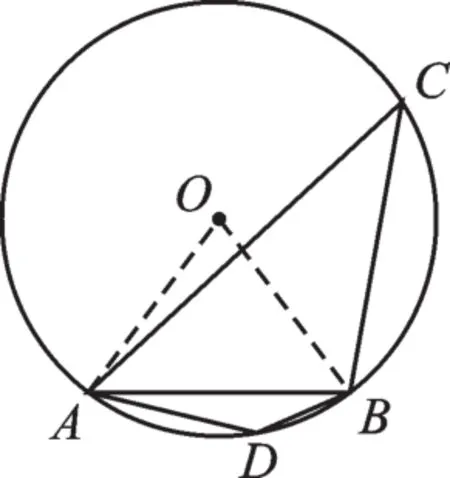
图1

【正解】30°或150°.

解：连接OA、OB，可得△AOB是等边三角形，即∠AOB=60°.

①当圆周角的顶点在优弧上时，则∠ACB=×60°=30°；

类型二：知圆心角求圆周角

例2如图2，扇形OAB的圆心角为122°，C是弧AB上一点，则∠ACB=_______.

图2

【错解】58°.

【错解原因】同学们以为∠ACB与∠AOB互补.出现这样的错误，主要是将四边形AOBC看成是圆内接四边形造成的.

【正解】119°.

【解法一】设点D是优弧AB上的一点，连接DA、DB，根据同弧所对的圆周角是圆心角的一半可求得∠D的度数，再根据圆内接四边形的对角互补，即可求得∠ACB的度数.

解：如图3，设点D是优弧AB上的一点，连接DA、DB.

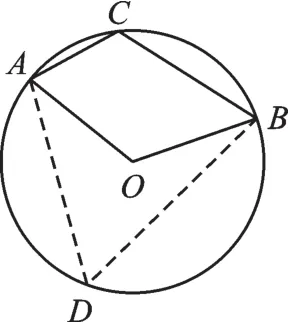
图3

∵∠AOB=122°，

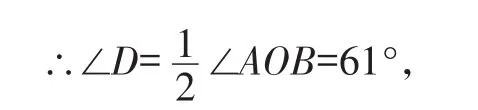
∴∠ACB=180°-∠D=119°.

【解法二】如图4.

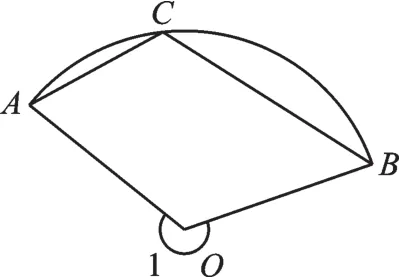
图4

∵∠AOB+∠1=360°，

∴∠1=360°-122°=238°，

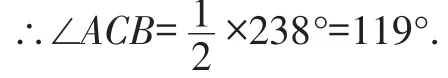
例3如图5，量角器外缘上有A，B两点，它们所表示的读数分别是80°、50°，则∠ACB应为（）.

A.25°B.15°C.30°D.50°

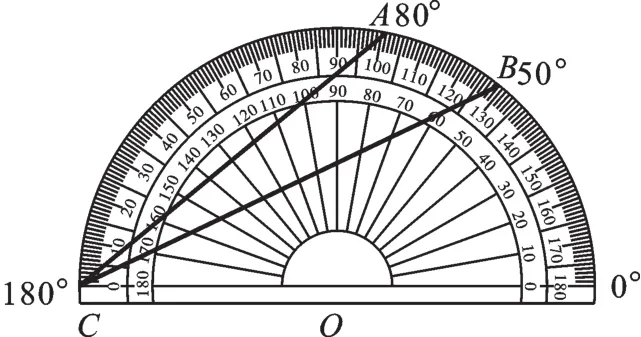
图5

【错解】C.

【错解原因】同学们对实际生活中的工具量角器如何量角原理理解不透，误把量角器的读数理解成圆周角的度数.

【正解】B.

【分析】连接OA、OB，根据量角器的读数，可得出∠AOB的度数，再根据圆周角定理即可求出∠ACB的度数.

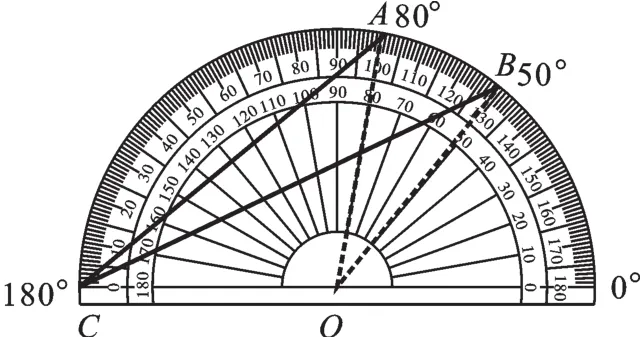
图6

解：如图6，设量角器的圆心是O，连接OA、OB，则∠AOB=80°-50°=30°，由圆周角定理得，∠ACB=15°.故选：B

类型三：知弧求圆周角

例4圆的一条弦把圆分成度数的比为1∶3的两段弧，则弧所对的圆周角等于（）.

A.45°B.90°

C.135°D.45°或135°

【错解】A或C.

【错解原因】弧有优弧与劣弧之分，部分同学在答题时容易只考虑其中的一种，解答不全面.

【正解】D.

【分析】由圆的一条弦把圆分成1∶3的两条弧，即可求得优弧、劣弧的度数，又由在同圆或等圆中，同弧或等弧所对的圆周角的度数等于这条弧度数的一半，即可求弧所对的圆周角的度数.

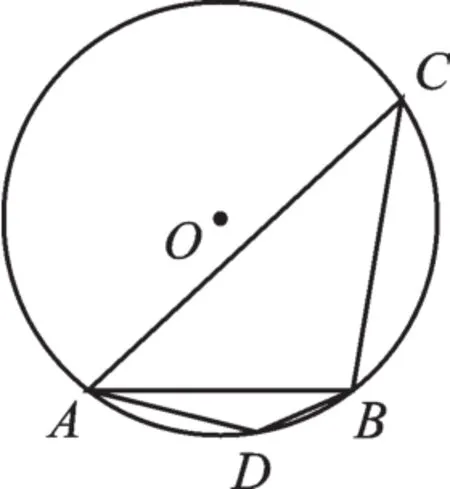
图7

解：如图7，∵AB把⊙O分成1∶3的两条弧，

∴劣弧AB度数为×360°=90°，优弧AB度数为×360°=270°，

∴∠C=×90°=45°，

∠D=×270°=135°.故选：D.

（作者单位：江苏省连云港市门河中学）