永磁直线同步电机自适应互补滑模控制

赵希梅， 王晨光， 程浩

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

永磁直线同步电机自适应互补滑模控制

赵希梅， 王晨光， 程浩

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

针对永磁直线同步电机(PMLSM)易受非线性因素影响而降低伺服系统鲁棒性的问题，提出一种自适应互补滑模控制方法。永磁直线同步电机的非线性因素包括系统参数变化、电机端部效应及外部不确定性的扰动。互补滑模控制将积分滑模面与广义误差滑模面相结合，将系统状态轨迹限定在两个面的交线上，缩短了状态轨迹达到滑模面的时间，提高了位置跟踪精度。为了进一步改善系统鲁棒跟踪性能，利用自适应控制对不确定扰动因素的上界进行估计，减小不确定因素对系统的影响，改善滑模控制的抖振现象。实验结果表明所提出的控制方法是有效可行的，自适应互补滑模控制不仅提高了系统的跟踪性能，而且更有效地抑制了不确定因素对控制系统的影响。

永磁直线同步电机；滑模控制；互补滑模控制；不确定性边界；自适应控制

0 引 言

随着现代工业技术的不断发展，传统的由旋转电机转成直线运动来加工零件的工艺已经达不到人们对工件加工精度的要求[1-2]。因此，在精密加工领域永磁直线同步电动机受到人们越来越多的关注，已经普遍应用于工业生产、军事航天、精密仪器仪表和医疗器械生产等领域[3-5]。PMLSM可以直接产生电磁推力，使得执行机构和被控对象之间不需要连接传动装置，消除了传动机构的机械摩擦和弹性形变，提高了控制系统的传动刚度和响应速度，刚度的提高使电机能够平稳运行，同时定位精度也得到改善[6]。虽然直驱电机有诸多优点，可是在系统控制上增加了难度。首先，不同于旋转电机气隙磁场的均匀分布，PMLSM初级两端开断的结构使电机两端的磁场比中间部分要弱，会引起端部效应和波形畸变的问题。其次，传动机构的消失使电机参数变化、外部扰动等因素无缓冲地直接作用在直线电机动子的运动过程中，给控制造成了很大困难，甚至影响加工精度[7]。因此，为了降低这些不确定性因素对伺服系统位置精度和动态响应时间的影响，要设计新的控制器对不确定性因素的值进行估计，满足系统控制上鲁棒性能和跟踪性能的要求。

滑模控制中滑动模态的设计可以不考虑被控对象参数和系统外部扰动的变化，具有响应速度快、鲁棒性强的优点[8]。但是，由于它采用了切换控制，在切换过程中存在的时间延迟、空间滞后和系统惯性，引起了系统在滑动模态下的高频振动，即抖振现象[9]。抖振不仅会降低系统控制精度，严重的话会使系统失去稳定性，损坏控制设备。为了削弱抖振，文献[10-12]采用了积分滑模面，使系统控制精度得到了改善，但忽略了滑模的降阶特性，计算较为复杂。文献[13]在边界层内采用了积分控制，减小了边界层厚度，虽然可以获得较小的稳态误差，但是它只能确保系统状态到达以滑模面为中心的边界层内，不能保证系统状态收敛到滑模面。

本文将互补滑模控制理论和自适应控制理论相结合，设计了一种自适应互补滑模控制器。互补滑模控制是在积分滑模面上增加一个广义误差的互补滑模面，将系统状态轨迹限定在两个滑模面的交线上，减少了状态轨迹到达滑模面的时间。在滑模控制中，系统鲁棒性主要体现在滑动模态，而在达到滑动模态之前的到达阶段，系统状态仍然受外部扰动等不确定性因素的影响，而且不确定性的边界范围很难确定。因此，引入自适应控制，用自适应律来估计不确定性的边界，将自适应控制和互补滑模控制的优点相结合，达到减小不确定因素对控制系统影响的目的。

1 永磁直线同步电机的数学模型

在磁场定向矢量控制id0的条件下，PMLSM的dq轴数学模型[14]如下。

电压方程

ud=Rsid+pΨd-ωΨq,

(1)

uq=Rsiq+pΨq+ωΨd。

(2)

式中：ud、uq，id、iq，Ψd、Ψq分别为动子d、q轴的电压、电流和磁链；Rs为定子电阻；p为微分算子，ω为角频率。

电磁推力方程

(3)

式中：Ld和Lq分别为d、q轴的电感，Ψf是永磁体产生的基波磁链；τ为极距;pn为极对数;Kf=3πpnΨf/2τ为电磁推力系数。

永磁体为表面安装式时Ld=Lq。因此，推力方程可以简化为

Fe=Kfiq。

(4)

机械运动方程

Mpv=Fe-Bv-FL。

(5)

式中：M为动子总质量；v为动子线速度;B为粘滞摩擦系数;FL为外部扰动。

将式(4)代入式(5)可得

(6)

2 系统设计

2.1 系统组成

PMLSM控制系统框图如图1所示，虚线框内为自适应互补滑模控制器结构图。控制系统主要由位置控制器、电流控制器、坐标变换、速度和位置检测单元组成。其中位置控制器具有快速响应输入信号的能力，对扰动具有良好的硬特性。电流控制器作为内环，将对电流的输入信号和检测信号进行综合判断和处理，从而有效地控制电枢电流，具有较高的快速性。速度和位置传感器主要用于采集电机实时的运行数据，反馈给控制器，对控制信号进行实时处理。

图1 PMLSM自适应互补滑模控制系统框图Fig.1 Block diagram of PMLSM adaptive complementary sliding mode control system

2.2 互补滑模控制

由PMLSM的数学模型得到速度方程(6)，如果将速度信号转换成位置信号，再考虑负载变化、机械摩擦产生的扰动时，式(6)可以重新整理为

(c+Δc)FL=

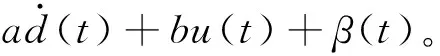
(7)

式中：d(t)是动子位移；a=-B/M；b=-Kf/M；c=-1/M；u(t)为控制量；Δa，Δb，Δc是非线性因素引起的参数变化量；β(t)是各个不确定项的集合，定义为

(8)

假设不确定项的边界为一常数

|β(t)|≤ρ。

(9)

式中，ρ是不确定项的上界，为一正常数。

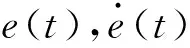
(10)

式中，λ是一个正常数。

将式(7)代入式(10)并求S1(t)的一阶导数：

(11)

互补滑模面定义为

(12)

定义两个滑模面的和为σ(t)

σ(t)=S1(t)+S2(t)。

(13)

滑模控制律由等效控制ueq和切换控制uv组成，等效控制决定了系统在滑模面上的动态性能，是迫使系统运动状态沿着滑模面运动所需要的控制力。切换控制是保证系统状态在有限时间内到达滑模面时所需要的控制力。

因此，滑模控制律可以设计为

u=ueq+uv。

(14)

在滑模面σ(t)=0时，求得等效控制

(15)

切换控制uv设计为

(16)

式中，Φ表示饱和函数边界层厚度，sat(·)表示饱和函数，ρ由(9)式定义。

(17)

2.3 自适应互补滑模控制

在互补滑模的切换控制中，控制增益ρ是不确定性扰动的上界，所以它的值将决定到达阶段的快速性和跟随性。因此，为了减小不确定性对控制系统的影响，采用自适应律对ρ的值进行估计。自适应互补滑模控制器框图如图2所示。

自适应律设计为

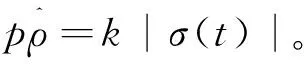
(18)

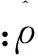
图2 自适应互补滑模控制框图Fig.2 Block diagram of adaptive complementary sliding mode control

通过对增益k的调整，可以改变自适应参数估计的变化率。由式(18)可以看出，k的大小与参数变化率成正比，但在实际中，k值不仅仅由控制输入决定，还受到其他条件的影响。

因此，式(16)的切换控制可以改写为

(19)

下面对系统稳定性进行分析：

依据李雅普诺夫稳定性判据，李雅普诺夫函数选择为

(20)

对李雅普诺夫函数求导并代入式(11)

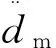
-λ(S1+S2)2+(S1+S2)(-buv)+

|S1+S2||β(t)|≤-λ(S1+S2)2+

|S1+S2|(|β(t)|-ρ)=

-λ(S1+S2)2-μ|S1+S2|≤0。

(21)

式中，|S1+S2|≥0，μ是一个正值，因此，系统在李雅普诺夫意义下是稳定的，保证了系统状态在有限时间内到达边界层。

3 系统实验结果分析

实验将TI公司生产的高性能TMS320LF2812A DSP作为执行单元，分别对采用互补滑模控制和自适应互补滑模控制方法的PMLSM控制系统进行实验研究，通过对比分析两种控制方法下的实验结果，验证所提出的控制方法的有效性。基于DSP的PMLSM控制系统结构如图3所示，主要包括整流逆变电路、上位机、DSP控制单元、电流检测单元及光栅尺位置检测单元。基于DSP的PMLSM控制系统实验平台如图4所示。

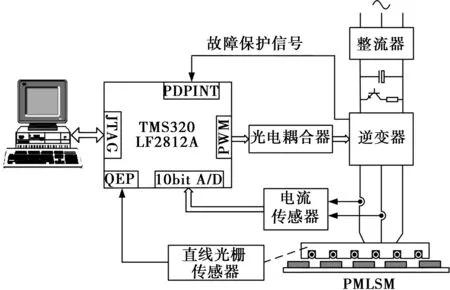
图3 基于DSP的PMLSM控制系统结构图Fig.3 Structure diagram of PMLSM control system based on DSP

图4 基于DSP的PMLSM伺服系统实验平台Fig.4 Experiment platform of PMLSM servo system based on DSP

为了验证所提出的控制方法的有效性，通过系统实验对比，分析基于互补滑模控制和自适应互补滑模控制的PMLSM伺服系统的实验结果。

实验中直线电机的参数为：pn=3，Rs=2.1 Ω，Ψf=0.09 Wb，Ld=Lq=41.4 mH，B=8.0 N·s/m，τ=32 mm，M=16.4 kg。PI电流控制器参数：kp=200，ki=400；滑模位置控制器参数为：ρ=4，Φ=0.001，k=13。实验中，检测单元将采样信号经AD转换后送入DSP中，通过DSP实现对电机的控制，对实验数据进行采样和处理，得到实验结果。

首先，位置信号给定为一个幅值为0.1 mm的阶跃信号，并在5 s时突加40 N的负载，采用两种控制方法的位置响应曲线如图5所示。从图5中可以看出，两种控制方法的跟随性能和快速性能都很好，相差不多，但在加入负载时，负载对自适应互补滑模控制系统的影响远小于对互补滑模控制系统的影响。如图5中局部放大图所示，采用互补滑模控制的曲线的波动幅度更大。

图5 阶跃信号给定下的跟踪响应曲线Fig.5 Tracking response curves for step signal input

当位置给定信号是一个幅值为0.2 mm的正弦信号时，在5 s时突加40 N的负载，两种控制方法下的位置跟踪响应曲线如图6所示。从图6中可以看出，两种控制方法在没有外部扰动的情况下都能准确跟踪给定的位置信号。但是在加入外部扰动后跟踪曲线都偏离了给定信号，从图6中的局部放大图可以看到，自适应互补滑模的波形波动幅度明显小于互补滑模的波动幅度。因此，自适应互补滑模控制在扰动下的跟随性能要优于互补滑模控制。

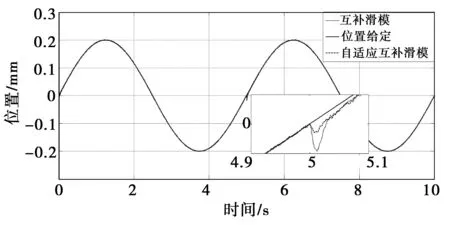
图6 正弦信号给定下的跟踪响应曲线Fig.6 Tracking response curves for sinusoidal signal input

在正弦信号下，互补滑模和自适应互补滑模的位置跟踪误差响应曲线如图7和图8所示，位置误差是给定位置信号与实际位置信号的差值，反映了控制系统的跟随性和鲁棒性。从图中可以明显看出，启动时互补滑模的误差约为23 μm，在5 s加入负载扰动时误差达到20 μm，而自适应互补滑模的对应值分别为15 μm和8 μm左右。虽然两者的快速性相差不多，但从鲁棒性上来看，自适应互补滑模有更好的表现。

图7 互补滑模控制跟踪误差曲线Fig.7 Tracking error curve of complementary sliding mode control

图8 自适应互补滑模控制跟踪误差曲线Fig.8 Tracking error curve of adaptive complementary sliding mode control

4 结 论

为了解决PMLSM易受控制系统参数变化和外部扰动影响的问题，基于滑模变结构控制具有鲁棒性强的特点，设计了自适应互补滑模控制器，通过实验验证了方法的可行性。

采用自适应控制估计不确定性因素的值，使互补滑模控制在到达阶段有更好的跟踪性和快速性，在一定程度上削弱了抖振现象。

在突加负载扰动时，自适应互补滑模控制方法能够有效减小伺服控制系统的位置跟踪误差，明显改善系统的跟踪性能和鲁棒性能。

[1] 郭庆鼎，王成元，周美文. 直线交流伺服系统的精密控制技术[M]. 北京：机械工业出版社，2000：1.

[2] 赵希梅，赵久威，李洪谊. 直驱 XY 平台伺服系统预测鲁棒轮廓跟踪控制[J]. 电机与控制学报，2014，18(6)：94. ZHAO Ximei，ZHAO Jiuwei，LI Hongyi. Predictive robust contour tracking control for direct drive XY table servo system [J].Electric Machines and Control，2014，18(6)：94．

[3] 赵希梅，孙显峰，刘浩，等. 周期性输入的直线伺服系统改进重复控制[J]. 电机与控制学报，2013，17(2)：112. ZHAO Ximei，SUN Xianfeng，LIU Hao，et al. Modified repetitive control of periodic input linear servo system[J].Electric Machines and Control，2013，17(2)：112．

[4] 严乐阳，叶佩青，张辉，等. 基于多周期迭代滑模控制的直线电机干扰抑制[J]. 电机与控制学报，2017，21(1)：8. YAN Yueyang，YE Peiqing，ZHANG Hui，et al. Disturbance rejection for linear motor based on multi-periodic learning variable structure control [J].Electric Machines and Control，2017，21(1)：8．

[5] 高庆忠，关焕新，于子淞，等. 自适应补偿器永磁同步电机积分性连续滑模控制[J]. 电机与控制学报，2017，21(2)：103. GAO Qingzhong，GUAN Huanxin，YU Zisong，et al. Integral continuous sliding mode control strategy with adaptive compensator for permanent magnet synchronous motor [J].Electric Machines and Control，2017，21(2)：103．

[6] LIN Chiying，CHEN Poying. Precision tracking control of a biaxial piezo stage using repetitive control and double-feed forward compensation[J]. Mechatronics，2011，21(1)：239.

[7] 王丽梅，张杰.基于模糊扰动裣的直接驱动XY平台轮廓控制[J].沈阳工业大学学报，2015，37(3)：241. WANG Limei,ZHANG Jie.Contour control for direct drive XY table based on fuzzy disturbance compensation[J].Journal of Shenyang University of Technology，2015，37(3)：241..

[8] 童克文，张兴，张昱,等. 基于新型趋近律的永磁同步电动机滑模变结构控制[J]. 中国电机工程学报，2008，28(21)：102. TONG Kewen，ZHANG Xing，ZHANG Yu，et al. Sliding mode variable structure control of permanent magnet synchronous machine based on a novel reaching law[J]. Proceedings of the CSEE，2008，28(21)：102.

[9] LIN F J，SHIEH P H,SHEN P H.Robust recurrent-neural-network sliding-mode control for the X-Y table of a CNC machine[J]. IEE Proceedings-Control Theory and Applications，2006，153(1)：111.

[10] CASTANOS F，FRIDMAN L．Analysis and design of integral sliding manifolds for systems with unmatched perturbations[J]．IEEE Transactions on Automatic Control，2006，51(5)：853．

[11] LEE Jung-Hoon，YOUN Myung-Joong. A new improved continuous variable structure controller for accurately prescribed tracking control of BLDD servo motors[J]. Automatica，2004，40(12)：2069.

[12] ABIDI K，XU J X，YU X. On the discrete-time integral sliding mode control[J]. IEEE Transactions on Automatic Control，2007，52(4)：709.

[13] SESHAGIRI.S，KHALIL HK. On Introducing Integral Action in Sliding Mode Control[C]//Proceedings of the 41st IEEE Conference on Decision and Control，Las Vegas.USA：2002，2：1473.

[14] 赵希梅. 高精度永磁直线同步电动机的二自由度鲁棒跟踪控制研究[D]. 沈阳：沈阳工业大学，2008.

Adaptivecomplementaryslidingmodecontrolforpermanentmagnetlinearsynchronousmotor

ZHAO Xi-mei， WANG Chen-guang， CHENG Hao

(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)

An adaptive complementary sliding mode control is proposed to solve the problem that the servo system of permanent magnet linear synchronous motor(PMLSM) is vulnerable to be affected by the nonlinear factors. The nonlinear factors of PMLSM include the variations of system parameter, the inherent end effect of motor, and the disturbance of the external uncertainty. Complementary sliding mode control combined the integral sliding surface and generalized error sliding surface,and the system state trajectory was defined in the intersection of two faces. Therefore, it shortened the time of the state trajectory to reach the sliding mode surface, and improved the position tracking accuracy. In order to further improve the robust tracking performance of the system, adaptive control was proposed to estimate the upper bound of uncertain disturbance factors. It can reduce the influence of the uncertain factors on the system, and improve the chattering phenomenon of sliding mode control. The experimental results show that the proposed control method is feasible and effective,and adaptive complementary sliding mode control not only improves the tracking performance of the system,but also effectively reduces the effects of uncertainty on the control system.

permanent magnet linear synchronous motor; sliding mode control; complementary sliding mode control; bound of uncertainty; adaptive control

(编辑：刘素菊)

2016-04-17

国家自然科学基金(51175349)；辽宁省自然科学基金项目(20170540677)

赵希梅(1979—)，女，博士，副教授，研究方向为直线伺服、数控技术、智能控制等； 王晨光(1990—)，男，硕士研究生，研究方向为直线伺服、智能控制等； 程 浩(1991—)，男，硕士研究生，研究方向为直线伺服、智能控制等。

赵希梅

10.15938/j.emc.2017.08.013

TP 273

:A

:1007-449X(2017)08-0095-06