采用拼接式转子的内置永磁同步电动机的优化设计

司萌， 杨向宇， 赵世伟， 司纪凯

(1.华南理工大学 电力学院，广东 广州 510640；2.国网重庆市电力公司电力科学研究院，重庆 401123；3.河南理工大学 电气工程与自动化学院，河南 焦作 454000)

采用拼接式转子的内置永磁同步电动机的优化设计

司萌1，2， 杨向宇1， 赵世伟1， 司纪凯3

(1.华南理工大学 电力学院，广东 广州 510640；2.国网重庆市电力公司电力科学研究院，重庆 401123；3.河南理工大学 电气工程与自动化学院，河南 焦作 454000)

针对传统内置永磁同步电动机漏磁系数较大，隔磁桥机械强度较差等特点，提出一种拼接式转子，这种转子具有若干个独立的铁心，用高强度非铁磁部件通过鸽尾形槽把这些铁心拼接起来，这种转子不需要隔磁桥，所以这种转子能够有效限制漏磁。拼接式转子的铁心具有一些磁障(空气槽)，这些磁障可以影响气隙内的磁场分布从而实现近似正弦分布的气隙磁密波形。初步设计了一台基于拼接式转子的3 kW电动机，采用田口法对转子磁障的关键参数进行了优化，并对拼接式转子和传统内置永磁转子进行了对比分析，结果表明所提出的拼接式转子优于传统内置永磁转子。

永磁同步电动机；拼接式转子；磁障；优化；田口法

0 引 言

内置永磁同步电动机具有效率高，功率密度高以及过载能力强等优点[1-3]，在各个领域中得到越来越广泛的应用。传统内置永磁转子需要利用隔磁桥限制漏磁，隔磁桥使转子铁心的机械强度较低，在加工转子冲片及装配转子时容易在隔磁桥处出现破损的情况，而且具有隔磁桥的转子漏磁仍然较大。护套式内置永磁转子采用分块转子铁心，在转子外圆处用高强度护套紧紧包裹起来，把转子的各个部件固定在应有的位置上。这种转子结构虽然取消了隔磁桥，与采用隔磁桥的普通转子结构相比，机械强度有一定提高。但是护套使电机的等效气隙较大，需要增加永磁体用量。上述转子结构产生的气隙磁密波形一般是矩形波，谐波含量较大。

文献[4-7]研究了一类利用非铁磁轴套固定转子铁心的切向内置永磁同步电动机，由于转子没有隔磁桥，这些电动机的漏磁能够被有效限制。这些电动机的转子轴套用高强度合金制成，所以可以保证转子具有足够高的机械强度。文献[6-9]所研究的电动机采用不均匀气隙改善气隙磁密波形。文献[10]采用不对称位置磁障降低了同步磁阻电动机的转矩波动，文献[11]对同步磁阻电动机的磁障形状进行了优化设计，有效降低了电动机的转矩波动。文献[12-13]研究了一种在内置永磁同步电动机转子铁心内设置磁障以改善气隙磁密的方法，使电动机的转矩波动有所降低。文献[14]提出了一种拼接式内置切向永磁转子，研究结果表明该转子结构具有多种优良特性。

本文提出一种拼接式内置径向永磁转子，这种转子具有若干个独立的铁心，用高强度非铁磁部件把这些铁心拼接成为一体。这种转子不需要隔磁桥，既可以有效限制漏磁，又可以保证其具有足够的机械强度。其中一些铁心具有可以改善气隙磁密波形的磁障，本文给出详细的磁障设计方法。

1 转子结构及工作机理

所提出的拼接式转子结构如图1所示，主要部件包括方形铁心、弓形铁心、永磁体、非铁磁部件以及转轴。方形铁心和弓形铁心均由硅钢片叠压而成。每个弓形铁心具有4个对称分布的磁障，这些磁障可以影响转子和气隙内的磁场分布，可以有效削弱气隙磁密谐波。用4个非铁磁部件通过鸽尾形槽把方形铁心和弓形铁心拼接起来。非铁磁部件可以用铍铜铸造，铍铜是一种高强度铜合金，可以保证转子具有足够高的机械强度以承受转子高速旋转时的离心力。拼接式转子没有隔磁桥，而且铍铜的导磁性能与空气的导磁性能接近，所以漏磁可以被有效限制。永磁体镶嵌在方形铁心和弓形铁心之间的槽内。

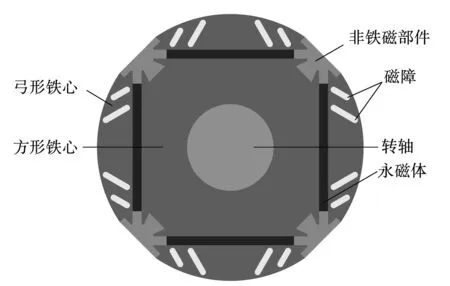
图1 拼接式转子结构示意图Fig.1 Spliced type rotor

2 电动机的初步设计

本节介绍一台3相4极3 kW电动机的初步设计。基于拼接式转子的新型电动机的设计过程与传统永磁同步电动机的设计过程基本一样，因为新型电动机与传统永磁同步电动机的不同之处在于两者转子结构的不同，所以本节着重介绍拼接式转子的设计方法。为了使非铁磁部件和弓形铁心具有足够的机械强度，并减少设计变量，指定电动机的极弧系数为0.75。假设在磁障的影响下新型电动机的气隙磁密是接近阶梯波形分布的，空载情况下一个极距内的气隙磁密近似波形如图2(a)所示，通过傅里叶变换可以得到n次分量的幅值

Bn= 2π∫απ0.125πB01sinnxdx+

2π∫βπαπB02sinnxdx+

2π∫(1-β)πβπB03sinnxdx+

2π∫(1-α)π(1-β)πB02sinnxdx+

2π∫0.875π(1-α)πB01sinnxdx=

4nπB01(cos0.125nπ-cosαnπ)+

4nπB02(cosαnπ-cosβnπ)+

4nπB03cosβnπ。

(1)

式中：n是奇数；B1是气隙磁密基波幅值；B01、B02和B03是图2(a)中的分段波形中不同段的幅值；α、β是气隙位置值系数；απ、βπ、(1-β)π和(1-α)π是图2(a)中分段波形的转折点对应的气隙位置值。

用γB03替代B01，用δB03替代B02，则Bn可以表示为

Bn= 4nπ(δ-γ)B03cosαnπ+

4nπ(1-δ)B03cosβnπ+

4nπγB03cos0.125nπ。

(2)

式中：γ是B01和B03的值之比；δ是B02和B03的值之比。

气隙磁密总谐波畸变率THD可以表示为式(3)，可见THD是α、β、γ和δ的函数。考虑前9次谐波，即3、5、7、…19次谐波，利用计算机求得在α=

0.216 2，β=0.310 7，γ=0.553 7，δ=0.775 2时THD取得最小值0.1508。

THD=∑n=3,5,7…B2nB1= ∑n=3,5,7…4nπ(δ-γ)B03cosαnπ+4nπ(1-δ)B03cosβnπ+4nπγB03cos0.125nπ24π(δ-γ)B03cosαπ+4π(1-δ)B03cosβπ+4πγB03cos0.125π=

∑n=3,5,7…1n(δ-γ)cosαnπ+1n(1-δ)cosβnπ+1nγcos0.125nπ2(δ-γ)cosαπ+(1-δ)cosβπ+γcos0.125π。

(3)

假设在磁障A、B的影响下，转子在一个极距范围内的空载磁通分布如图2(b)所示，总磁通包括三个主要部分：Φ1、Φ2和Φ3，箭头表示磁通的方向。磁障与弓形铁心表面距离最小处决定了磁通的不同部分在气隙及永磁体中的边界。在保持磁障与弓形铁心表面的最小距离不变的前提下改变磁障的形状和位置，则气隙磁场的分布会受到影响。在图2(b)中，α1、α2和α3分别是对应于Φ1、Φ2和Φ3在气隙中的分布范围的圆心角，τ是极距角，bm是每个永磁体的宽度，k1是Φ1通过的永磁体部分宽度与永磁体宽度的比值，k2是Φ2通过的永磁体部分宽度与永磁体宽度的比值。α1、α2、α3、k1和k2的值受到磁障形状变化的影响。如果α1、α2、α3、k1和k2的值已给定，就可以根据这些值选择永磁体尺寸的初始值。

为了实现接近于图2(a)所示的气隙磁密波形，磁障的形状应使α1、α2和α3满足以下等式：

α1=(α-0.125)τ，

(4)

α2=(β-α)τ，

(5)

α3=(0.5-β)τ。

(6)

式中：α=0.2162，β=0.3107。

根据以上条件，可以建立一个简化等效磁路模型，如图2(c)所示。k1、k2的理想值可以通过求解这个简化等效磁路模型得到。永磁体的每一部分都用一个磁势源和磁阻串联而成的等效模型来表示，F是磁势源的计算磁动势，Rm是每个永磁体的磁阻，Rδ是一个极距下气隙磁阻(按均匀部分的厚度计算)。根据气隙各部分的截面占每极下气隙总截面的比例，以及永磁体各部分占每个永磁体总截面的比例，可以得到气隙及永磁体各部分的磁阻，如图2(c)所示。

Φ1、Φ2和Φ3分别按照下式计算：

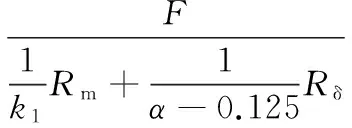
(7)

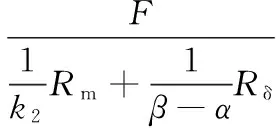
(8)

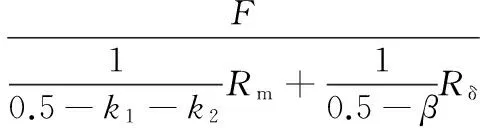
(9)

图2(a)中的B01、B02和B03分别按照下式计算：

(10)

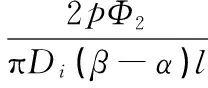
(11)

(12)

式中：p是极对数；Di是定子内径；l是定子和转子的轴向长度。

B01和B03之间的理想关系，以及B02和B03之间的理想关系可以分别表示为：

B01=γB03，

(13)

B02=δB03。

(14)

(15)

求解此方程组可得到k1和k2的理想值。

为了能在短时间内完成优化设计，有必要设置一些限制条件。磁障A、B的形状及位置取决于其中心线的形状及位置，如图3所示。磁障A、B的轮廓由其中心线(ac、bd)向外侧偏移得到，为了获得理想的隔磁效果并减少设计变量，设定偏移距离为1mm。磁障A、B的中心线节点a、b、c和d在距弓形铁心轮廓d0的线上，为了使磁障对磁通有有效的引导作用，设定d0长度为1.5mm。在图3中，O是转子中心，OM和ON是极对称轴。在以上限制条件下，磁障A、B的形状及位置取决于四个设计变量：Oa与极对称轴的夹角θ1，Ob与极对称轴的夹角θ2，节点c与极对称轴的距离d1，节点d与极对称轴的距离d2。通过调整这四个设计变量就可以调整气隙磁密波形。

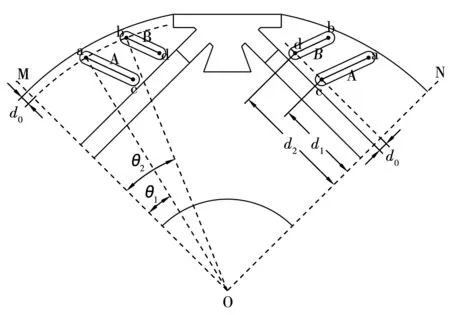
图3 设计变量Fig.3 Design variables

通过初步设计得到一台3kW电动机的设计结果，主要参数在表1中给出。

表1 设计结果Table 1 Design results

3 转子的优化设计

转子磁障参数对气隙磁场分布有显著影响，而利用简化等效磁路设计得到的转子参数未必是最佳参数，所以需要对转子进行优化设计。理论上通过全因子试验可以得到最佳参数组合，但是全因子试验往往代价很高。田口法是一种用于改善产品质量的优化方法，采用正交表来安排试验计划。采用正交表可以对特定因素对试验指标的效应进行单独评估，通过较少次数的试验得到最令人满意的优化结果。田口法非常适宜于解决电机优化问题[15-19]，所以可以采用田口法对拼接式转子的磁障进行优化设计。

3.1 试验计划

共有4个因素：X1，X2，X3及X4，对应于转子磁障的4个设计变量(θ1，θ2，d1和d2)，如表2所示。每个因素有三个水平，每个因素的不同水平对应的变量值从初始值附近的小范围内取得，并且它们成等差数列。

表2 因素的水平Table 2 Levels of each factor

标准正交表可以处理大多数2～4水平因素的优化问题。根据表2中的因素及水平数，选择标准正交表L-9(34)来实施优化设计。表名L-9(34)意为该表有9行4列，可以处理4个三水平因素的试验设计问题。基于标准正交表L-9(34)的试验计划如表3所示，每个因素的水平号在对应该因素的列中给出，括号内是水平号对应的设计变量值。从表2中可见，全因子试验需要34=81次试验，而采用标准正交表L-9(34)仅需要9次试验。

根据表3中的设计变量组合对新型电动机进行了二维有限元分析，得到了每种设计变量组合对应的气隙磁密波形。本节分析4个设计变量对B1和THD的影响。由于气隙磁密波形前4次谐波(3、5、7、9)的幅值相对较大，本节着重考虑前4次谐波对THD的影响，计算THD时仅将前4次谐波考虑在内。每次试验对应的B1和THD的值在表4中给出。

表3 基于L-9(34)的试验计划Table 3 Experimental plan based on L-9(34)

表4 B1和THD的计算结果Table 4 Calculation results of B1 and THD

3.2 结果分析

根据表4计算总平均值为

(16)

式中：S是B1或THD；i是试验序号；S(i)是从第i次试验中得到的B1或THD的值。比如，从第1次试验中得到的THD值用THD(1)表示。

从所有试验中得到的M(S)计算结果如表5所示。

表5 总平均值Table 5 Overall means

j水平的因素X对S的效应用MX(j)(S)表示，X对应于4个因素X1，X2，X3及X4，j对应于3个水平号。MX(j)(S)可以根据表3和表4计算，比如，水平2的因素X3对THD的效应为

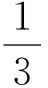
THD(4)+THD(9)]。

(17)

其他因素对试验指标的效应按照类似的方法计算得到，计算结果在图4中给出。

为了评估各因素的相对重要性，需要计算各效应值相对于总平均值的离差平方和SSDX(S)，即为

(18)

SSDX(S)计算结果在表6中给出，这些计算结果反映了不同因素对B1和THD效应的比重。

图4 因素对试验指标的效应图Fig.4 Plots of factor effects on the experimental indexes

B1THDSSD比重(%)SSD比重(%)X11.64×10-64.508.34×10-59.31X27.24×10-619.872.30×10-425.71X31.20×10-63.311.38×10-415.37X42.63×10-572.334.44×10-449.61总计3.64×10-51008.95×10-4100

3.3 确定优化变量组合

根据图4和表6可以确定最佳设计变量组合。从表6可见因素X4对B1有决定性影响，B1应该被最大化，从图4(a)可见X4应该选择水平3。X1、X2和X3的水平选择应该着重于使THD最小化，根据图4(b)可见X1、X2和X3应分别选择水平1、水平1和水平3。最终确定优化设计变量组合为[X1(1),X2(1),X3(3),X4(3)]。

4 对比分析

齿槽转矩和反电动势谐波是引起永磁同步电动机转矩波动的两个重要原因。气隙磁场的分布情况对反电动势波形有明显影响，所以可以通过削弱气隙磁密波形来削弱转矩波动。为了证实拼接式转子的优越性，对传统内置径向式永磁转子结构、第2节的拼接式转子初始设计结构和第3节的拼接式转子优化设计结构进行对比分析。基于上述3种转子结构的电动机的定子结构、绕组布局、转子外径、永磁体尺寸以及极弧系数都相同，3者的主要区别在于转子结构不同。

4.1 气隙磁密波形

通过二维有限元分析得到3种结构的空载气隙磁密波形如图5(a)、图5(b)和图5(c)所示，分量幅值如图5(d)所示。从图5(a)、图5(b)和图5(c)可见初始设计和优化设计的气隙磁密波形比传统设计的气隙磁密波形更接近正弦波形。从图5(d)可见初始设计和优化设计的气隙磁密基波幅值明显高于传统设计的气隙磁密基波幅值，初始设计和优化设计的气隙磁密谐波幅值明显低于传统结构的气隙磁密谐波幅值。

图5 空载气隙磁密波形及分量Fig.5 Air gap flux density waveforms under no load condition and their components

图6 空载相反电动势波形及分量Fig.6 Phase back EMF waveforms under no load condition and their components

4.2 空载相反电动势波形

3种设计的永磁体尺寸完全相同，但它们转子结构的不同导致它们有不同的气隙磁密基波幅值，如图5(d)所示。所以有必要根据传统设计的气隙磁密基波幅值为传统设计指定不同于初始设计的每相串联匝数。通过瞬态二维有限元分析得到3种设计在1 500转每分情况下的空载相反电动势波形如图6(a)、图6(b)和图6(c)所示，分量幅值如图6(d)所示。从图6(a)、图6(b)和图6(c)可见初始设计和优化设计的相反电动势波形比传统设计的相反电动势波形更接近正弦波形。从图6(d)可见初始设计和优化设计的相反电动势基波幅值明显高于传统设计的相反电动势基波幅，初始设计和优化设计的相反电动势谐波幅值明显低于传统结构的相反电动势谐波幅值。

4.3 额定运行状态输出转矩波形

通过瞬态二维有限元分析得到了3种设计对应的额定运行状态输出转矩波形，如图7所示。转矩波动情况可以用转矩波动系数Kr来衡量，即为

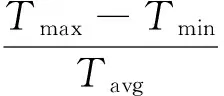
(19)

式中：Tmax是转矩最大值；Tmin是转矩最小值；Tavg是平均转矩。

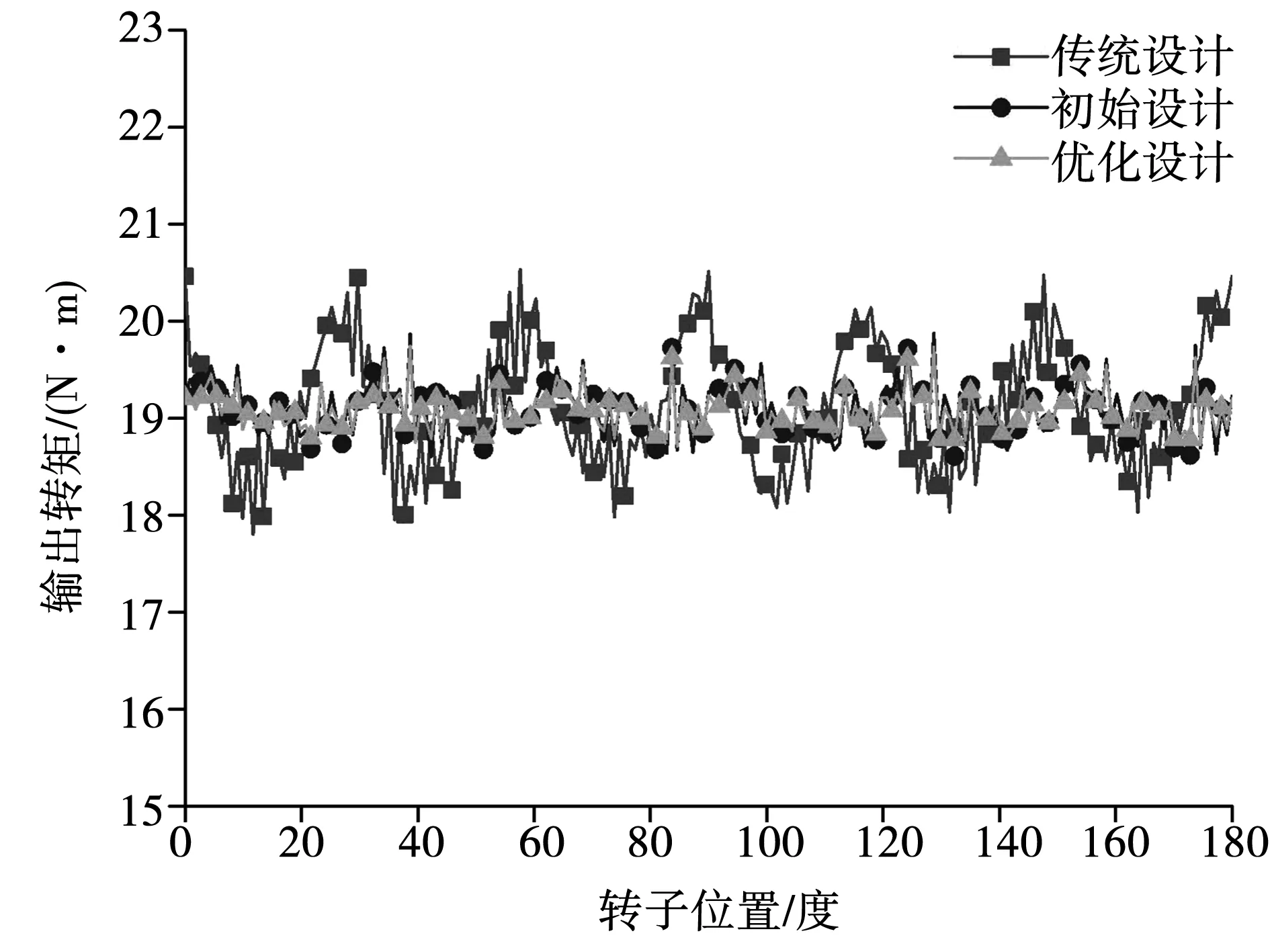
图7 额定运行状态输出转矩曲线Fig.7 Output torque waveforms under rated operating condition

通过计算得到3种设计的转矩波动系数并在表7中给出，可见初始设计和优化设计的转矩波动明显小于传统设计。

表7 转矩波动Table 7 Torque ripples

4.4 空载漏磁系数

通过二维有限元分析得到了3种设计的空载磁通分布图如图8所示。空载漏磁系数计算方法如下[1]：

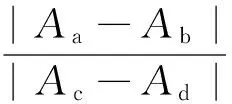
(20)

(21)

(22)

式中：σ1是传统设计的空载漏磁系数；σ2是初始设计的空载漏磁系数；σ3是优化设计的空载漏磁系数；Aa～Al是图8中标有相应字母的点处的磁矢位值。

从图8中可见传统设计的漏磁对应的磁力线数目多于初始设计和优化设计。Aa～Al的值从图8中得到，根据Aa～Al的值计算得到σ1、σ2和σ3的值，这些值在表8中给出。从图8和表8中可见初始设计和优化设计的漏磁明显低于传统设计。

表8 磁矢位值及漏磁系数值

图8 空载磁通分布图Fig.8 Magnetic flux distribution plots under no load condition

5 结 论

本文提出了一种拼接式径向永磁转子，并给出了一种基于等效磁路法的解析模型以进行初步设计。采用田口法对拼接式转子磁障的关键参数进行了优化。最后，将拼接式转子与传统内置径向式永磁转子进行了对比分析，对比结果表明优化结果令人满意，拼接式转子在气隙磁密波形、反电动势波形、输出转矩以及漏磁方面均明显优于传统内置径向式永磁转子。

[1] 唐任远.现代永磁电机理论与设计[M].北京: 机械工业出版社,1997.

[2] 霍品如,王旭东,侯博雅.IPMSM定子电流最优控制策略仿真研究[J].哈尔滨理工大学学报,2012,17(2): 89. HUO Pinru,WANG Xudong,HOU Boya.Simulation research on optimal stator current control strategy of IPMSM[J].Journal of Harbin University of Science and Technology,2012,17(2): 89.

[3] 林瑞全,黄韬,张涛.一种内置式永磁同步电机复合转速估计方法[J].哈尔滨理工大学学报,2012,17(4): 1. LIN Ruiquan,HUANG Tao,ZHANG Tao.A composite speed estimation algorithm of IPMSM [J].Journal of Harbin University of Science and Technology,2012,17(4):1.

[4] ELREFAIE A M,ALEXANDER J P,GALIOTO S,et al.Advanced high-power-density interior permanent magnet motor for traction applications[J].IEEE Transactions on Industry Applications,2014,50(5): 3235.

[5] GALIOTO S J,REDDY P B,ELREFAIE A M,et al.Effect of magnet types on performance of high-speed spoke interior-permanent-magnet machines designed for traction applications[J].IEEE Transactions on Industry Applications,2015,51(3):2148.

[6] HUANG Z,HUANG X,ZHANG J,et al.Design of an interior permanent magnet synchronous traction motor for high speed railway applications[C]//6th IET International Conference on Power Electronics,Machines and Drives (PEMD 2012),Bristol,UK,2012: 1.

[7] DEMIR Y,OCAK O,AYDIN M.Design,optimization and manufacturing of a spoke type interior permanent magnet synchronous motor for low voltage-high current servo applications[C]//2013 IEEE International Electric Machines & Drives Conference (IEMDC),Chicago,IL,USA,2013:9.

[8] WU Shihua,SONG Liwei,CUI Shumei.Study on improving the performance of permanent magnet wheel motor for the electric vehicle application[J].IEEE Transactions on Magnetics,2007,43(1):438.

[9] CARRARO E,BIANCHI N.Design and comparison of interior permanent magnet synchronous motors with non-uniform airgap and conventional rotor for electric vehicle applications[J].IET Electric Power Applications,2014,8(6):240.

[10] SANADA M,HIRAMOTO K,MORIMOTO S,et al.Torque ripple improvement for synchronous reluctance motor using an asymmetric flux barrier arrangement[J].IEEE Transactions on Industry Applications,2004,40(4):1076.

[11] BIANCHI N,BOLOGNANI S,BON D,et al.Rotor flux-barrier design for torque ripple reduction in synchronous reluctance and PM-assisted synchronous reluctance motors[J].IEEE Transactions on Industry Applications,2009,45(3): 921.

[12] YANG B,PARK H,KWON B.Design of flux barrier for reducing torque ripple and cogging torque in IPM type BLDC motor[C]//2006 12th Biennial IEEE Conference on Electromagnetic Field Computation,Miami,FL,USA,2006: 241.

[13] JANG J,KIM H,SONG J,et al.Design of flux barriers in a rotor of an interior PM synchronous motor for reducing harmonics losses[C]//2010 14th Biennial IEEE Conference on Electromagnetic Field Computation,Chicago,IL,USA,2010: 1.

[14] SI Meng,YANG Xiangyu,ZHAO Shiwei,et al.Design and analysis of a novel spoke type permanent magnet synchronous motor[J].IET Electric Power Applications,2016,10(6): 571.

[15] 兰志勇,杨向宇,王芳媛,等.Taguchi方法在内嵌式正弦波永磁同步电机优化设计中的应用[J].电工技术学报,2011,26(12)：37. LAN Zhiyong,YANG Xiangyu,WANG Fangyuan,et al.Application for optimal designing of sinusoidal interior permanent magnet synchronous motors by using the taguchi method [J].Transactions of China Electrotechnical Society,2011,26(12)：37.

[16] 龚晟,杨向宇,纪梁洲.磁阻型无刷双馈电机特殊转子优化设计[J].电力自动化设备,2012,32(8),60. GONG Sheng,YANG Xiangyu,JI Liangzhou.Optimal design of special reluctance rotor for brushless doubly-fed motor [J].Electric Power Automation Equipment,2012,32(8):60.

[17] KIM S,LEE J,KIM Y,et al.Optimization for reduction of torque ripple in interior permanent magnet motor by using the taguchi method [J].IEEE Transactions on Magnetics,2005,41(5):1796.

[18] LEE S,KIM K,CHO S,et al.Optimal design of interior permanent magnet synchronous motor considering the manufacturing tolerances using taguchi robust design[J].IET Electric Power Applications,2014,8(1): 23.

[19] HWANG C,HUNG S,LIU C,et al.Optimal design of a high speed spm motor for machine tool applications [J].IEEE Transactions on Magnetics,2014,50(1):1.

(编辑：贾志超)

Optimaldesignofaninteriorpermanentmagnetsynchronousmotorwithasplicedtyperotor

SI Meng1，2， YANG Xiang-yu1， ZHAO Shi-wei1， SI Ji-kai3

(1.School of Electric Power,South China University of Technology,Guangzhou 510640,China; 2.State Grid Chongqing Electric Power Corporation Chongqing Power Research Institude,Chongqing 401123,China; 3.School of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo 454000,China)

Considering that the flux leakage coefficients of conventional interior permanent magnet synchronous motors (IPMSM) are relatively high,and the mechanical strengths of the rotor bridges are relatively low,a kind of spliced type rotor is proposed.The spliced type rotor has several individual iron core parts,which are spliced together by high strength nonmagnetic components using dovetail slots.The rotor does not require bridges,and hence the leakage flux of the rotor can be restricted effectively.There are several flux barriers (air slots) in the iron core parts of the spliced type rotor,and these flux barriers can influence the magnetic field distributions in the air gap and realize a near-sinusoidal air gap flux density waveform.The initial design parameters of a 3 kW motor based on the spliced type rotor were obtained from the initial design process,and several key parameters of the rotor flux barriers were optimized by using the Taguchi method.A comparative analysis of the spliced type rotor and a conventional interior permanent magnet rotor was performed,and the comparative analysis results show that the spliced type rotor is superior to the conventional interior permanent magnet rotor.

permanent magnet synchronous motor; spliced type rotor; flux barrier; optimization; Taguchi method

2016-04-19

国家自然科学基金(U1361109，51107041)

司 萌(1987—)，男，博士研究生，研究方向为特种电机及其控制； 杨向宇(1963—)，男，博士，教授，博士生导师，研究方向为特种电机及其控制； 赵世伟(1977—)，男，博士，副教授，硕士生导师，研究方向为特种电机及其控制； 司纪凯(1973—)，男，博士，副教授，硕士生导师，研究方向为特种电机及其控制。

司 萌

10.15938/j.emc.2017.08.009

TM 351

:A

:1007-449X(2017)08-0062-10