双向隔离型DC-DC变换器的双移相优化控制

王毅， 许恺， 陈骥群

(1.华北电力大学(保定) 新能源电力系统国家重点实验室，河北 保定 071003；2.河北省电力公司保定供电局，河北 保定 071051)

双向隔离型DC-DC变换器的双移相优化控制

王毅1， 许恺2， 陈骥群2

(1.华北电力大学(保定) 新能源电力系统国家重点实验室，河北 保定 071003；2.河北省电力公司保定供电局，河北 保定 071051)

针对双向隔离型DC-DC变换器采用双移相控制策略时会减小开关管实现“软开关”的范围，使系统效率降低的问题，提出了一种优化控制算法。该控制算法以抑制系统回流功率和扩大开关管软开关范围为约束条件，优选出系统的最优运行点。搭建了硬件电路，对所提控制策略进行验证，可知系统在该最优运行点下，回流功率仅为传输有功功率的1%，同时系统效率也达到了最高。实验结果表明，采用所提的优化控制算法能够协调系统对开关管“软开关”的范围和回流功率的要求，使系统在满足桥臂功率管“软开关”条件的同时，得到更小的回流功率。

双向DC-DC全桥；双移相；回流功率；软开关；优化控制

0 引 言

使用电力电子变压器取代传统工频变压器为机车牵引系统供电，对其小型化和轻量化有重要意义，因而成为牵引传动系统向高速、大功率方向的发展的新热点[1-6]。双向隔离型DC-DC变换器因具有高可靠性、高功率密度、功率双向流动等特点[7-12]，已成为电力电子牵引变压器(power electronic traction transformer，PETT)高频化的核心变换单元，其电路参数和控制系统设计对PETT性能有重要影响。由于在为PETT进行设计时需综合考虑减重、效率以及供电质量等不同指标要求，因而对双向隔离型DC-DC变换器的优化设计提出了更高的要求。

在设备高频化减重的同时，随着开关频率的提高使变换器中功率管的开关损耗有所增加，导致系统变换效率降低。为此，双向隔离型DC-DC变换器控制方式通常采用移相控制策略[13-17]。传统的单移相控制较为成熟，通过调节原副边电压的相角差，即可实现对传输功率的大小和方向的控制[18-19]。它具有容易实现“软开关”、动态响应快等优点。功率管通过“软开关”，可有效减小变换器开关损耗，提高系统效率。然而由于单移相控制为单自由度控制，无法对回流功率进行有效抑制，较高的回流功率将导致变换器产生较高的电流应力和输出电压纹波。其中，较高的电流应力不利于电力电子器件的选择；较大的电压纹波，则需增加直流滤波电容器的容量，不利于牵引变压器轻量化的实现。为此有学者提出了双移相控制策略[20]，在桥臂外移相的基础上加入桥臂内移相。文献[21]对双移相控制下变换器传输功率、回流功率和电流应力特性进行了深入研究，但未对双移相控制下变换器开关管的“软开关”特性进行深入分析。文献[22]指出在双移相控制下，增大内移相角可使变换器的回流功率得到有效抑制，但同时使开关管的“软开关”范围减小，导致系统效率降低。在以上研究的基础上，提出一种基于最小回流功率的闭环控制策略，该方法可有效地抑制变换器的回流功率，减小系统损耗，提高变换器的效率。然而该控制算法未考虑了功率开关管的“软开关”范围裕度以及变换器在牵引变压器系统中的应用，其性能指标的优化设计还不完善。

首先对双移相控制策略回流功率和软开关特性以及二者的关系进行深入研究，并在此基础上，提出一种双移相优化控制算法，该控制算法考虑了功率开关管“软开关”范围裕度，通过内移相角的优选，有效减小变换器的回流功率和系统损耗，从而提高变换器的效率以及PETT的综合性能。

1 双向隔离型DC-DC变换器数学模型的构建

1.1 电路拓扑

图1为电力电子牵引变压器整机拓扑结构图，DC-DC变换器为其重要组成部分。此处主要针对双向全桥隔离型DC-DC变换器控制策略进行研究，其拓扑结构如图2所示。图中Tr为高频变压器，变比为n，L为将变压器漏感归算至原边的等效电感。Vdc1和Vdc2为变换器两侧等效电压。

图1 电力电子牵引变压器整机拓扑结构图Fig.1 Overall unit topology structure diagram of power electronic traction transformer

图2 全桥隔离型DC-DC变换器拓扑结构Fig.2 Topology of the full bridge isolated DC-DC converter

1.2 双移相控制工作原理

为便于构建双向隔离型DC-DC变换器在双移相控制下的数学模型，下文将介绍双移相控制的工作原理。

双移相控制是一种在原副边桥外移相的基础上，加入单侧桥壁内移相的控制方式。在单移相控制下，由于相移的存在，在有功功率传输过程中，电感电流与原边侧电压存在相位相反的阶段，此时传输功率为负，即功率回流到电源中，此功率称为回流功率。在传输功率一定时，回流功率增加，将增大电感电流应力及磁性元件的损耗，降低了变换器效率。

图3为双移相控制时直流变换器工作波形。为表示方便，开关管S1的驱动信号用其名称S1来表示，其他开关管表示方法同此。VAB为原边侧逆变输出电压，VCD为副边侧逆变输出电压折合到Vdc1侧后的电压；VL为变压器等值电感两侧电压；Ths为半个开关周期；D1为变换器半周期内原边侧全桥的内移相度，D2为变换器半周期内原边侧全桥和副边侧全桥的外移相度。采用双移相控制时，由于内移相度D1的引入，使变压器原边侧电压为0，如在t0～t1及t4～t5时段内，此时回流功率为0，功率环流得到有效抑制，进而提高了功率传输效率。

图3 双移相控制时直流变换器工作波形Fig.3 Waveforms of DC converter in dual phase shift control

1.3 变换器数学模型建立

基于双移相控制工作原理，下面构建双向隔离型DC-DC变换器在双移相控制下的数学模型，由图3可得：

(1)

(2)

(3)

(4)

(5)

(6)

假定t0=0，则有t1=D1Ths，t3=(D1+D2)Ths，t4=Ths，t5=Ths+D1Ths，t7=Ths+(D1+D2)Ths，t8=2Ths。其中，D1为内移相度，D2为外移相度，Ths为半周期时间。由式(1)～式(6)，根据正负周期对称性可得：

(7)

(8)

(9)

双移相控制下，变换器输出有功功率为

(10)

设功率基值为

(11)

经单位化可得：

(12)

2 双移相控制特性分析

由于在移相控制下影响双向隔离型DC-DC变换器性能指标的主要因素是系统回流功率和功率开关管的“软开关”范围，为此下文将对二者进行重点分析。

2.1 回流功率分析

根据回流功率的定义[23]，由图3得到双移相控制下，变换器回流功率的表达式

(13)

经单位化可得：

(14)

下面以电压增益k=2为例，说明回流功率与移相度之间的关系。

图4为电压增益k=2时回流功率与移相度的关系曲线，从中可知回流功率随着内移相度D1的增加而减小。即通过增加内移相度D1可有效抑制系统的回流功率。

图4 回流功率与移相度关系曲线(k=2)Fig.4 Relationship curve of backflow power and phase shift ratio(k=2)

2.2 “软开关”范围分析

原边桥“软开关”条件

(15)

即

(16)

副边桥“软开关”条件

(17)

即

(18)

(19)

(20)

经单位化可得：

(21)

(22)

图5为软开关范围与移相度的关系曲线，从中可知随着内移相度D1的增加功率开关管“软开关”范围减小，将不利于开关管实现“软开关”，开关损耗将增大，使变换器效率下降。

通过上述分析可知，虽然增加内移相度D1，可有效抑制变换器回流功率，使其具有更小的电流应力和输出电压纹波，但同时也减小了功率开关管“软开关”范围，导致系统效率降低。为此下文将介绍一种双移相控制下的优化控制算法，通过对内移相度D1的优选，协调变换器对回流功率和“软开关”范围的要求。

图5 软开关范围与移相度关系曲线Fig.5 Relationship curve between soft-switching range and phase-shiftratio

3 双移相优化控制算法

3.1 优化函数的构建

通过上文研究可知，开关管“软开关”范围和变换器回流功率是影响双向隔离型DC-DC变换器性能指标的重要因素，且二者相互制约。为此提出一种双移相控制策略下的优化控制算法，以开关管“软开关”范围和变换器回流功率作为约束条件，构建系统的优化函数。

基于开关管“软开关”范围的约束条件，定义函数z1

(23)

显然z1越大，原副边桥开关管“软开关”范围越大，原副变桥开关管越容易实现“软开关”，变换器效率越高。

基于变换器回流功率的约束条件，定义函数z2

(24)

显然，z2取值越小，变换器回流功率越小，相应的电流应力和输出电压纹波也越小，对改善变换器电能质量越有利。

为协调变换器回流功率和开关管“软开关”范围，定义优化函数m′

m′(D1,D2)=z2-z1。

(25)

由上述分析可知，当z1取得最大值而z2取得最小值时，系统达到最优运行状态，此时m′取得最小值。m′与移相度之间的关系曲线如图6所示，从中可知，在给定外移相度D2下，必存在唯一的内移相度D1，使m′取得最小值，系统达到最优运行方式。此时桥臂功率开关管在获得在最大“软开关”范围同时，得到该条件下的最小回流功率。

图6 m′与移相度之间的关系曲线(k=2)Fig.6 Relationship curve between m′and phase shift ratio(k=2)

3.2 不同电压增益下优化函数的构建

根据实际应用中对变换器输出直流电压的不同需求，下面将研究在不同电压增益k下优化函数的构建。将不同电压增益k下，使系统达到最优运行状态时的内外移相度组合进行拟合，可得到不同电压增益k下使系统运行状态达到最优时的函数表达式：

(26)

(27)

(28)

(29)

在给定传输功率下，存在多组(D1，D2)的取值组合，可满足给定传输功率的要求。但这些组合未必都是系统的最优运行点。在给定传输功率和电压增益k下，根据式(26)～式(29)和式(10)即可唯一确定一组(D1，D2)，使系统运行状态最优。由式(26)～式(29)，绘制最优运行状态下D2随D1变化的曲线图，如图7所示，该曲线对指导系统运行具有一定意义。

图7 最优运行曲线Fig.7 Optimal operating curve

3.3 优化控制策略的研究

图8给出了采用的闭环控制框图。双移相优化控制策略为：根据双向DC-DC直流变换器输出有功功率P′以及电压增益k，按在最优运行情况下，内移相度和外移相度之间的关系式计算并设定内移相度D1。在给定D1下，通过闭环调节外移相度D2控制输出电压的恒定。闭环控制器采用常用的PI控制器。

图8 系统闭环控制框图Fig.8 Block diagram of system close-loop control

4 实验结果

4.1 实验参数的选取

为验证上述分析与研究的正确性，按照图2所示拓扑结构并根据实验室实验条件搭建双向全桥DC-DC变换器系统实验平台。它主要由高频变压器以及全桥开关电路组成。

1)移相度的确定

依据图8给出的系统闭环控制框图，可以采用基本PI控制器，完成给定内移相D1下的外移相D2的闭环调节，以保证输出电压的恒定。设定输出有功功率P′=667 W，输入直流电压Vdc1=100 V，输出直流电压Vdc2=50 V，考虑到原副边桥开关管电压应力的匹配问题，将高频变压器变比n设定为1∶1。根据设计的电压增益k与输出有功功率P′，由式(10)和式(27)计算可得使系统达到该条件下最优运行状态时的内移相度：D1=0.33。

2)高频变压器参数的选取

由于变压器的频率与体积成反比例关系，因而从实现变压器减重和减小体积方面考虑，应使变压器额定频率尽可能地大。然而，由于高频带来的器件开关损耗增大，使变压器整体效率降低，且考虑到安全的需要，全桥开关电路的开关频率f设为3 kHz。

通过信号发生器测量在开关频率f=3 kHz下高频变压器原副边漏电阻R11=R12=0.04 Ω，原副边漏电感L11=L12=87.5 μH。

3)直流支撑电容的选取

为了限制负载扰动时的直流电压动态变化，支撑电容应该比较大。要求变换器满足负载扰动时的抗干扰性能指标ΔU0max，则支撑电容的容值应该满足[25]

(30)

根据输出有功功率P′与输出直流电压Vdc2得到输出直流电流Io为13.34 A，ΔU0max设定为输出直流电压的5%，带入上式可得Cmin=1.78 mF。

但在实际的电路中，元器件存在的杂散参数使得必须选用大于的电容值才能达到纹波要求，一般选取2～4倍的Cmin值。在本设计中采用5 mF电容。

相关实验参数如表1所示。

表1 DC-DC变换器实验参数Table 1 Experimental parameters of DC-DC converter

在不影响实验效果的前提下，为了简化硬件电路的设计过程，采用光伏电池模拟器来得到DC-DC变换器所需的直流电压，接入到变换器的输入端。实验系统结构图如图9所示。图10为搭建的系统实物图。

图9 双向全桥DC-DC变换器系统结构图Fig.9 Structure of the bidirectional full bridge DC-DC converter

图10 双向全桥DC-DC变换器系统实物图Fig.10 Picture of the experimental platform of bidirectional full-bridge DC-DC converter system

4.2 实验结果

图11为双移相控制在不同内移相度下的变压器两端电压电流波形。从中可知，当内移相度D1=0.33时，在该工况下原边桥输出电压的零电平恰好使系统的回流功率为0，如图11(b)圈注所示。此外，通过对比不同内移相度下电感电流最大应力可知，随着内移相度的增加，电感电流最大应力将逐渐减小，这是因为随着内移相度D1的增加，系统的回流功率得到了有效抑制，提高了功率传输效率，减小了正向传输的总功率，从而减小了电感电流应力。

图11 变压器两端电压电流实验波形Fig.11 Experimental waveforms of VAB，VCD，and iL

图12与图14分别为内移相度为0.2和0.5时原副边桥开关管电压电流波形。通过对比可知，在内移相度为0.2时，原边桥开关管为大电流关断，如图12(a)圈注所示。在内移相度为0.5时，原边桥开关管为大电流开通，副边桥开关管为大电流关断，如图14(a)和图14(b)圈注所示。而在内移相度D1=0.33时原副边桥开关管同时实现了零电流开通和零电流关断，如图13所示。

图12 D1=0.2时的原副边桥开关管电压电流实验波形Fig.12 Experimental waveforms of VS1VQ1iL(D1=0.2)

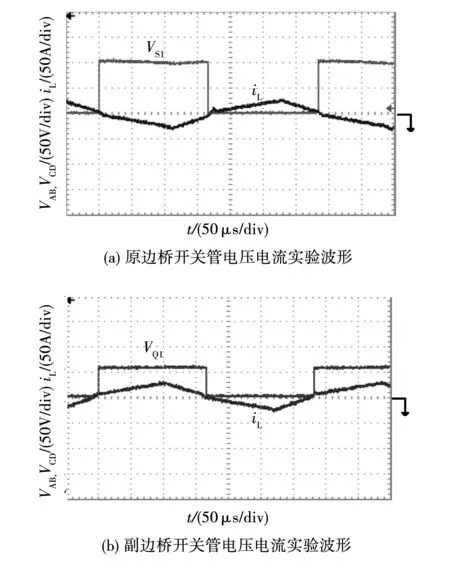
图13 D1=0.33时的原副边桥开关管电压电流实验波形Fig.13 Experimental waveforms of VS1VQ1iL(D1=0.33)

图14 D1=0.5时的原副边桥开关管电压电流实验波形Fig.14 Experimental waveforms of VS1VQ1iL (D1=0.5)

图15 实测回流功率及效率与内移相度D1的关系Fig.15 Tested backflow power and efficiency curves with different D1

图15给出了变换器实测回流功率及效率与内移相度D1的关系曲线。内移相度D1由0～0.5变化，通过外移相度D2，保持输出电压为50 V不变，进而保证电压增益k以及传输有功功率不变。从图可知，随着内移相度D1的增加回流功率得到了有效抑制，然而由于内移相度的增加，导致开关管“软开关”范围减小，实际工作点偏离“软开关”区域，使变换器效率急剧降低。当内移相度D1在0.33附近时系统整体效率最高，与理论分析基本一致。

5 结 论

本文重点分析了双向隔离型DC-DC变换器在双移相控制下的软开关特性与功率回流特性，以及二者之间的关系，并在此基础上提出了一种双移相优化控制算法，该算法以扩大开关管“软开关”范围和减小变换器回流功率为约束条件，通过构建优化函数得到了在特定负载条件下函数值与移相度的关系曲线，从中得到一组可使变换器运行于最优状态下的移相角，并通过曲线拟合的方法得到了在不同负载条件下变换器最优运行曲线及其对应的拟合函数表达式。实验结果表明，采用本文提出的优化控制算法在使全部桥臂开关管实现“软开关”的同时，有效抑制了变换器的回流功率，提高了变换器的效率。从而使电力电子牵引变压器可同时满足效率、减重和电能质量方面的要求。

[1] RONAN E R,SUDHOFF S D,GLOVER S F,et al.A power electronic-based distribution transformer[J].IEEE Trans on Power Delivery,2002,17(2):537.

[2] KANG M,ENJETI P N,PITEL I J.Analysis and design of electronic transformers for electric power distribution system[J].IEEE Transactions on Power Electronics,1999,14(6):1133.

[3] MANJREKAR M D,KIEFERNDORF R,VENKATARAMANAN G.Power electronic transformers for utility[C]//Conference Record of the 2000 IEEE Industry Application Conference,Vol 4.Piscataway(NJ):2000.2496.

[4] HARADA K,ANAN F,YAMASAKI K,et al.Intelligent transformer[C]//Conference of IEEE PESC.[s.l.],1996,1337.

[5] 周美兰,赵立萍.电动汽车复合储能系统的能量控制策略与仿真[J].哈尔滨理工大学学报,2016,(03):8. ZHOU Meilan,ZHAO Liping.Energy management strategy design and simulation for electric vehicles compound energy storage system[J].Journal of Harbin University of Science and Technology,2016,(03):8.

[6] 朱显辉,崔淑梅,师楠,等.双向DC变换器拓扑的电动汽车电磁干扰仿真[J].哈尔滨理工大学学报,2012,(04):18. ZHU Xianhui,CUI Shumei,SHI Nan,et al.EMI simulation of electric vehicle with bi-directional DC transformer topology[J].Journal of Harbin University of Science and Technology,2012,(04):18.

[7] JONGPIL L， BYUNG D M，DONG W Y，et al.A new topology for PV DC/DC converter with high efficiency under wide load range[C]//Power Electronics and Applications,European Conference,Sept 2-5,2007:1.

[8] HUANG J C，LI W L．A bidirectional DC-DC converter for fuel cell electric vehicle driving system[J].IEEE Transactions on Power Electronics， 2006， 21(4)： 950．

[9] SHIGENORI I，HIROFUMI A．A bidirectional isolated DC-DC converter as a core circuit of the next-generation medium-voltage power conversion system[J]．IEEE Transactions on Power Electronics， 2007， 22(2)： 535．

[10] SEBASTIAN J,LAMAR D G,HERNANDO M M,et al.An overall study of a dual active bridge for bidirectional DC/DC conversion[C]//Energy Conversion Congress and Exposition,September 12-16,Univ.de Oviedo,Gijon,Spain,2010:1129.

[11] 赵彪，于庆广，王立雯，等．具有馈电功能的新型并网UPS系统及其分散逻辑控制策略[J]．中国电机工程学报，2011，31(31)：85． ZHAO Biao，YU Qingguang，WANG Liwen，et al．Novel grid-connected UPS system with the electricity feedback function and its distributed logic control strategy[J]．Proceedings of the CSEE，2011，31(31):85．

[12] 周美兰,田小晨.用于电动汽车的交错并联软开关双向DC/DC变换器[J].哈尔滨理工大学学报,2016,(04):83. ZHOU Meilan,TIAN Xiaochen.An Interleaved soft-switching bidirectional DC/DC converter in electric vehicles[J].Journal of Harbin University of Science and Technology,2016,(04):83.

[13] 赵彪,于庆广,王立雯.Z源双向DC-DC变换器及其移相直通控制策略[J].中国电机工程学报,2011,31(09):43. ZHAO Biao，YU Qingguang，WANG Liwen．A Z-source bi-directional DC/DC converter and its phase shifting-short control strategy[J]．Proceedings of the CSEE，2011，31(9):43.

[14] 孙铁成,郭超,娜仁图亚,等.具有移相控制的ZVS全桥DC-DC斩波变换器[J].电工技术学报,2014,12(29):66. SUN Tiecheng，GUO Chao，NAREN Tuya，et al.A novel DC-DC ZVS full-bridge converter based on phase-shift control[J].Transactions of Electrotechnical Soiety ,2014,12(29):66.

[15] AMIT K J,RAJAPANDIAN A.PWM control of dual active bridge:comprehensive analysis and experimental verification[J].Power Electronics,IEEE Transactions on,2011,26(4):1215.

[16] MI C,BAI H,WANG C,et al.Operation,design and control of dual H-bridge-based isolated bidirectional DC-DC converter[J].IET Power Electronics,2008,1(4):507.

[17] 赵川红,徐德鸿,范海峰,等.PWM加相移控制的双向DC/DC变换器[J].中国电机工程学报,2003,23(10):72. ZHAO Chuanhong， XU Dehong， FAN Haifeng，et al.A PWM plus phase-shift control bidirectional DC/DC converter[J]．Proceedings of the CSEE，2003，23(10)：72．

[18] XIE Yanhui,SUN Jing.Power flow characterization of a bidirectional galvanically isolated high-power DC/DC converter over a wide operating range[J].Power Electronics,IEEE Transactions on,2010,25(1):54.

[19] JAIN M,DANIELE M,JAIN P K.A bidirectional DC-DC converter topology for low power application[C]//IEEE Trans.Power Electron,July 15 2000:595.

[20] 张相军, 刘冠男, 王懿杰,等. 软开关双向DC-DC变换器控制模型[J]. 电机与控制学报, 2013, 17(11):89. ZHANG Xiangjun, LIU Guannan, WANG Yijie, et al. Bidirectional DC/DC converter control model analysis based on super capacitor[J]. Electric Machines and Control, 2013, 17(11):89.

[21] 武琳, 张燕枝, 李子欣,等. 一种隔离式双向全桥DC/DC变换器的控制策略[J].电机与控制学报, 2012, 16(12):21. WU Lin, ZHANG Yanzhi, LI Zixin, et al. A control strategy of isolated bidirectional full bridge DC/DC converter[J].Electric Machines and Control, 2012, 16(12):21.

[22] 程红,高巧梅,朱锦标,等.基于双重移相控制的双向全桥DC-DC变换器动态建模与最小回流功率控制[J].电工技术学报,2014,03(29):245. CHENG Hong，GAO Qiaomei，ZHU Jinbiao，et al.Dynamic modeling and minimum backflow power controlling of the bi-directional full-bridge DC-DC converters based on dual-phase-shifting control[J].Transactions of Electrotechnical Soiety,2014,03(29):245.

[23] ZHAO Biao,YU Qingguang.Extended-phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J].Power Electronics,IEEE Transactions on,2012,27(11): 4667.

[24] 蒋玮,胡仁杰,黄慧春.移相控制对称半桥变换器软开关条件[J].电工技术学报,2011,26(11):8. JIANG Wei，HU Renjie，HUANG Huichun.ZVS condition of symmetry half-bridge converter with phase-shifted control[J].Transactions of Electrotechnical Soiety,2011,26(11):8.

[25] ABRAHAM I.PRESSMAN,KEITH B,等.开关电源设计[M].北京：电子工业出版社，2012:68.

Dual-phase-shiftingoptimizationcontrolofisolatedDC-DCconverter

WANG Yi1， XU Kai2， CHEN Ji-qun2

(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources,North China Electrical Power University,Baoding 071003,China; 2.Baoding Electric Power Bureau,Hebei Electric Power Company,Baoding 071051,China)

The bidirectional isolation DC-DC converter adopts dual-phase-shifting control strategy, which will narrow the range of “soft-switching” and lower the efficiency of the system. To solve this problem, an optimal control algorithm is proposed. The control algorithm suppresses the backflow power of the system and extends the soft-switching range of the switch tube.Considering this constraint, the optimal operating point of the system was then selected. The hardware circuit was built and the control strategy was verified. It was found that at the optimal operating point, the backflow power of the system is only 1% of the active power and the system efficiency is the highest. Experimental results show that the optimized control algorithm can be used to coordinate the range of “soft-switching” and the requirement of backflow power of the switch, so that the system can meet the requirement of “soft-switching” of the bridge arm power tube and obtain smaller backflow power.

bidirectional DC-DC full bridge; dual-phase-shifting; backflow power; soft-switching; optimal control

(编辑：贾志超)

2015-11-25

国家重点研发计划(2016YFB0900203)

王 毅(1977—)，男，博士，教授，研究方向为新能源发电，电力电电力电子技术与应用； 许 恺(1990—)，男，硕士研究生，研究方向为轻型动车牵引电子电力变压器； 陈骥群(1990—)，女，硕士研究生，研究方向为电力系统的运行、分析与控制。

许 恺

10.15938/j.emc.2017.08.008

TM 417

:A

:1007-449X(2017)08-0053-09