汽轮发电机转子阻尼结构对大扰动低频振荡的影响

许国瑞， 李金香， 付永旗， 胡笳， 孙玉田， 刘晓芳

(1.华北电力大学 电气与电子工程学院，北京 102206；2.水力发电设备国家重点实验室(哈尔滨大电机研究所)，黑龙江 哈尔滨 100084；3.中国电力国际有限公司，北京100080)

汽轮发电机转子阻尼结构对大扰动低频振荡的影响

许国瑞1， 李金香2， 付永旗1， 胡笳3， 孙玉田2， 刘晓芳1

(1.华北电力大学 电气与电子工程学院，北京 102206；2.水力发电设备国家重点实验室(哈尔滨大电机研究所)，黑龙江 哈尔滨 100084；3.中国电力国际有限公司，北京100080)

为了研究汽轮发电机转子大齿导条、导电槽楔和转子铁心等转子阻尼结构在大扰动低频振荡过程中的作用，首先建立了用于研究大扰动低频振荡过程中汽轮发电机转子各部分阻尼结构作用的场-路耦合时步有限元模型，并通过实验进行了验证；然后采用该模型研究了汽轮发电机转子各部分阻尼结构大扰动低频振荡过程中的作用，分析了三部分阻尼单独作用和共同作用时，对大扰动低频振荡影响较大的阻尼结构；最后研究了不同材料转子槽楔对汽轮发电大扰动低频振荡过程的影响。结果表明：汽轮发电机转子阻尼作用可以有效抑制大扰动后的低频振荡过程；在三部分阻尼中转子槽楔所起的作用较大，且转子采用铝合金槽楔对于抑制大扰动低频振荡的效果明显好于不锈钢槽楔。

转子阻尼结构；大扰动；低频振荡；汽轮发电机；时步有限元

0 引 言

发电机容量的提升及远距离输电的发展增加了电力系统发生低频振荡的概率，尤其是当电网发生大扰动后机组之间过大的功角摆动幅度极易造成发电机的失步和电网的解列[1-3]。通常情况下，充足的系统阻尼对于抑制低频振荡起着至关重要作用[4]，而汽轮发电机转子本体结构的阻尼作用是系统总阻尼的重要组成部分，它通常包括转子大齿导条、转子铁心和转子导电槽楔[5-6]，如图1所示，转子各部分阻尼的结构和材料特性不同导致其产生的阻尼作用及抑制低频振荡的能力也不同。因此，研究汽轮发电机转子各部分阻尼结构对大扰动低频振荡的作用是十分必要的。

图1 汽轮发电机三部分阻尼结构Fig.1 Three component of damping structure of turbine generator

国内外的文献对发电机小扰动引起的低频振荡原因和机理进行了大量研究，并取得了较多的成果[7-10]。然而，对于大扰动引起的发电机及系统的低频振荡问题，尤其是全面深入考虑汽轮发电机转子各部分阻尼结构作用下的低频振荡问题还没有深入研究。传统的发电机电路模型通常采用等效阻尼参数来模拟实际的转子阻尼结构[11-12]，然而汽轮发电机转子铁心通常由整块钢锻造且转子槽楔、导条等阻尼结构分布不均匀，这些因素使得阻尼等效参数难以精确计算，如果再考虑到磁路饱和以及集肤效应的影响，这些参数就更加难以精确计算了[13]。因此，系统仿真分析中通常采用降阶的发电机模型，由于这些模型引入了假设条件使得计算结果的精确性难以保证。同时，系统发生大扰动后发电机通常会进入电磁和机电暂态共存的连续扰动过程，如果不能准确考虑发电机转子阻尼结构会使得发电机大扰动后低频振荡区域发生变化，进而会影响励磁控制器、电力系统稳定器等发电机辅助设备的参数整定[14]。

发电机的时步有限元模型可以全面有效的计及转子各部分阻尼结构的作用，也可以充分考虑磁路饱和、磁场畸变和集肤效应等非线性因素对转子阻尼作用的影响[18-19]。文献[15-17]等采用时步有限元法计算和分析了发电机动态特性和参数，并取得了较好的结果。文献[2021]中采用时步有限元模型计算发电机空载突然短路过程并与实测结果进行对比，结果非常接近。因此，采用时步有限元法来研究系统大扰动低频振荡过程中汽轮发电机转子各部分阻尼结构的作用可以满足精确度的要求。

本文首先建立了用于研究大扰动低频振荡过程中汽轮发电机转子阻尼作用的场-路耦合时步有限元模型，并通过模型机实验对所建立的模型进行了验证；然后采用该模型研究了汽轮发电机转子阻尼结构作用对大扰动低频振荡的影响，具体分析了转子三部分阻尼结构单独作用和共同作用时，对大扰动低频振荡影响较大的阻尼结构；最后研究了转子导电槽楔采用不同材料对汽轮发电机大扰动低频振荡的影响。研究结果可为汽轮发电机转子阻尼结构的优化设计以及如何提高发电机承受系统低频振荡能力提供理论支持。

1 仿真模型的建立

1.1 充分考虑转子三部分阻尼结构作用的时步有限元模型

采用二维有限元模型，在麦克斯韦方程组的基础上推导得到发电机的场-路耦合方程如式(1)所示[19]。

(1)

式中：A为矢量磁位，Is为定子电流矩阵，可表示为[iA,iB,iC]，if为励磁电流，rs和ls为定子绕组的电阻和端部漏感，rf和lf为转子绕组的电阻和端部漏感，Rs=diag[rs,rs,rs]，Ls=diag[ls,ls,ls]，Ul为定子电压矩阵，可表示为[uA,uB,uC]，K为刚度矩阵，Cs为定子电流的关联矩阵，Ds、Dd和Dr分别为转子导电槽楔、大齿导条和转子铁心涡流的关联矩阵，Cf为励磁电流的关联矩阵，lef为轴长。

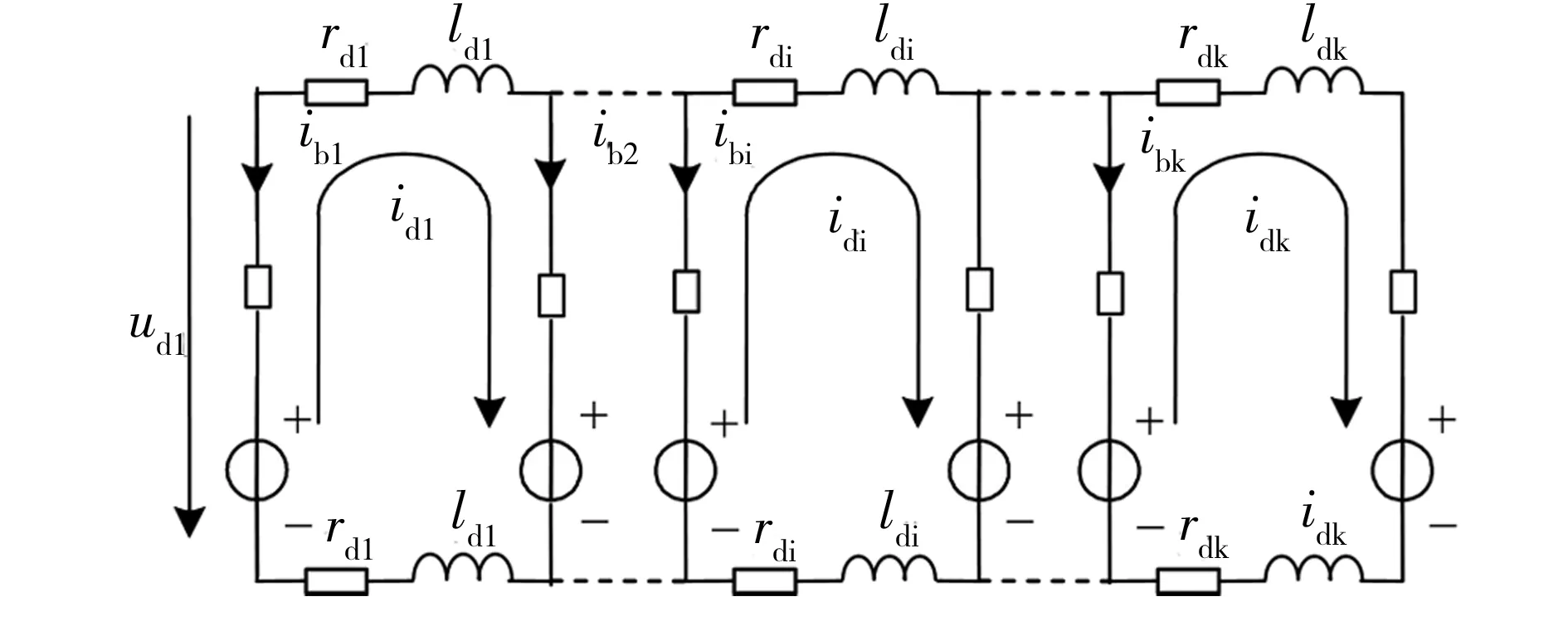
图2 阻尼回路模型Fig.2 Damping circuit model

为了精确计及由转子导电槽楔、大齿导条及端环构成的阻尼绕组的作用，采用对转子阻尼绕组回路列写方程的方法进行计算。阻尼回路模型如图2所示，其中，rdi、ldi分别为阻尼端环的电阻与漏电感，ibi为转子槽楔或大齿导条中的电流，idi为各个回路的电流，udi为槽楔或大齿导条两端的电压。

转子大齿导条与导电槽楔直线部分各点的电流密度Jdi可表示为

(2)

式中转子大齿导条和导电槽楔的电导率统一用σ来表示。

根据图2中所示的正方向，列写各支路的电流方程和回路的电压方程可得到式(3)。

(3)

结合式(2)与式(3)，经过有限元离散可得阻尼回路方程为：

(4)

式中：Ud=[ud1…udi…udk]T，Id=[id1…idi…idk]T，Rd=diag[2rd1,…,2rdk]，Ld=diag[2ld1,…,2ldk]，Hd1=diag[σS1/lef,…,σS1/lef]。

将转子阻尼绕组中电流密度表达式(2)代入磁场方程，经过加权积分变换后可得到磁场方程的有限元表达式(5)。

(5)

结合方程(1)、(4)和(5)，可得充分考虑汽轮发电机转子阻尼结构的场-路耦合时步有限元模型：

(6)

1.2 实验验证

为了验证上述所建立模型的准确性，本文以实验室7.5 kW 模型机为基础，搭建了单机接升压变压器并通过双回线连接无穷大电网的实验平台，通过该平台进行了系统大扰动的实验并与仿真进行了对比。其中，模型机的参数如表1所示，实验平台如图3所示。

图3 同步发电机动态实验测试平台Fig.3 Dynamic experiment platform of synchronous generator

参数300MW发电机7.5kW模型机功率/kW3000007.5额定功率因数0.850.85额定电压/V20000400额定电流/A1020012.73额定励磁电流/A25008转速/(r/min)30003000

以直流电动机作为原动机将发电机模型机拖动到同步转速，然后施加励磁电流使其达到并网条件后并入电网，调节原动机和励磁电电流使模型机运行在某一负载工况并稳定运行。在变压器高压侧的一回线首端施加三相接地短路故障，经过0.1 s后切除故障线路，模型机通过单回线向系统供电。将时步有限元的计算结果与上述实测结果进行对比，得到模型机的励磁电流、定子电流和转速的波形曲线如图4所示。从图中可以看出仿真与实测结果拟合较好。

2 转子阻尼结构对大扰动低频振荡的影响

本文采用如图5所示系统仿真模型来研究系统大扰动低频振荡过程中汽轮发电机转子三部分阻尼结构的作用。图中：UG为发电机出口端电压，UT为变压器高压侧电压，US为无穷大系统母线电压。文中所采用的汽轮发电机额定参数如表1所示。汽轮发电机的定转子结构及转子三部分阻尼结构如图1所示，阻尼结构所用材料及其电导率如表2所示。本文所采用的大扰动条件为：当系统运行在某一稳定工况时，任意时刻在单回线的首段F点施加三相接地短路故障，故障持续0.1s后切除该线路，此时发电机通过单回线向电网供电，系统的供电方式发生变化。在大扰动激励下，发电机系统发生低频振荡。

表2 转子三部分阻尼结构的材料及相应的电导率

图4 实测和仿真结果对比Fig.4 Simulation results of T-S FEM compared with the testing

图5 单机无穷大系统动态仿真模型Fig.5 Dynamic simulation model of single-machine infinite-bus system

2.1 转子阻尼计及与否对大扰动低频振荡的影响

采用时步有限元模型分别对转子阻尼作用计及与否情况下的大扰动低频振荡进行仿真计算，得出大扰动后发电机的功角和角速度曲线如图6所示。

从图6中可以看出：

1)当不计转子阻尼作用时，功角的最大幅值为59.89°，而计及转子阻尼作用后最大幅值变为41.51°，较前者减小了18.38°，可以看出汽轮发电机转子各部分阻尼结构的作用可以有效抑制大扰动过程中的功角和角速度的幅值。

2)当不计转子阻尼作用时，功角曲线接近等幅振荡，衰减时间常数很大，而计及转子阻尼作用后，功角曲线很快衰减，衰减时间常数减小为2.151 s。可以看出转子阻尼作用也可以明显减小大扰动低频振荡的衰减时间常数。

从上述结果可以看出，汽轮发电机转子阻尼作用对系统大扰动及其引起的机-网之间的低频振荡过程具有明显的抑制作用。

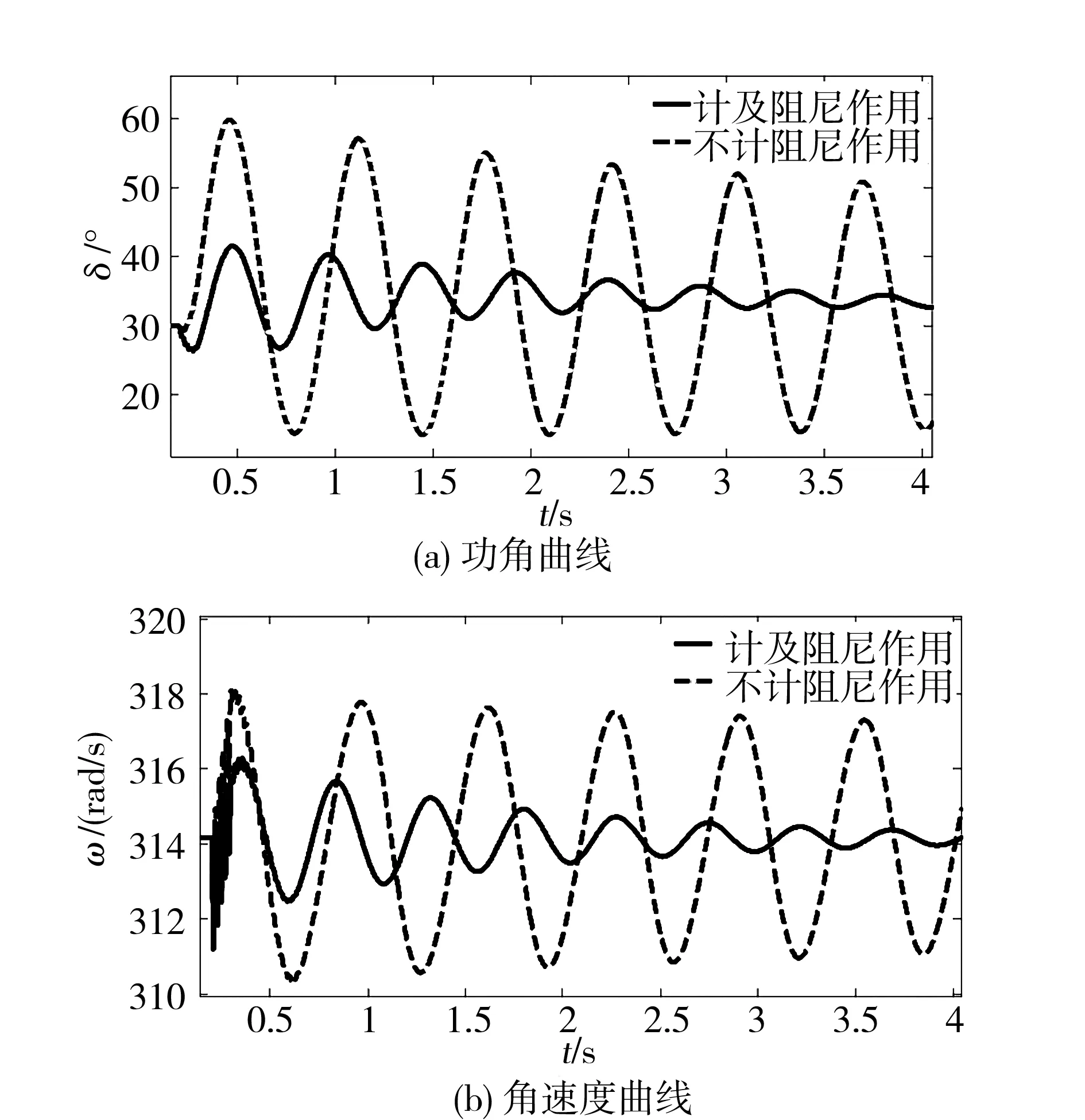
图6 转子阻尼计及与否时大扰动功角曲线与角速度曲线Fig.6 Power angle and angular velocity curves after large disturbance with and without rotor damping effects

2.2 转子各部分阻尼单独作用对大扰动低频振荡的影响

汽轮发电机的转子阻尼结构通常由大齿导条、导电槽楔和铁心三部分构成，为了研究这三部分阻尼在大扰动过程的作用及其对机-网低频振荡幅值和衰减时间常数的影响，本节对转子三部分阻尼单独作用下的大扰动过程进行仿真对比，其结果如图7所示。为了定量化的对比和分析仿真结果的差异，本文通过Prony法对三种情况下计算的角速度曲线进行拟合，得出大扰动低频振荡过程中发电机转子角速度的振荡频率和阻尼比，结果如表3所示。

图7 三部分阻尼单独作用时的功角与角速度曲线Fig.7 Power angle and angular velocity curves under separately effect of three damping structures

λ1,2f/Hzζ转子槽楔-1.1±j5.96901.90.18123转子铁心-0.91±j5.34071.70.16790大齿导条-0.41±j5.96901.90.06852

从图7和表3中可以看出：

1)转子导电槽楔单独作用时，功角与角速度曲线的振荡幅值最小；而转子铁心单独作用时，功角与角速度曲线的振荡幅值最大。因此，转子导电槽楔对于功角与角速度最大幅值的抑制作用比较明显。

2)转子导电槽楔、铁心及大齿导条分别作用时，角速度曲线的衰减时间常数分别为0.81 s、0.98 s、2.2 s。转子导电槽楔对于大扰动后低频振荡的快速衰减作用比较明显。

3)转子导电槽楔单独作用时的阻尼比最大，而大齿导条单独作用时的阻尼比最小，说明转子三种阻尼结构单独作用时，转子导电槽楔的作用最强。

2.3 转子各部分阻尼共同作用对大扰动低频振荡的影响

本节对汽轮发电机各部分阻尼共同作用时的大扰动低频振荡过程进行研究。首先对仅计转子大齿导条、计及转子大齿导条和导电槽楔、计及转子大齿导条和铁心这三种情况下的大扰动低频振荡过程进行对比，结果如图8(a)所示。从图中可以看出，仅计转子大齿导条作用时系统功角的振荡幅值较大，功角最大幅值为50.75°；而转子大齿导条和导电槽楔共同作用以及转子大齿导条和铁心共同作用时，系统功角的最大幅值分别为41.55°与41.6°，振荡幅值明显减小且功角曲线也更快达到稳态值。

然后对仅计转子铁心、计及转子铁心和导电槽楔、计及转子铁心和大齿导条等三种情况下的大扰动低频振荡过程进行对比，结果如图8(b)所示。从图中可以看出，仅计转子铁心作用时系统功角的振荡幅值较大，功角最大幅值为52.38°；而转子铁心和导电槽楔共同作用以及转子铁心和大齿导条共同作用时系统功角的最大幅值分别为42.36°与41.6°，振荡幅值均明显减小。

最后对仅计转子导电槽楔、计及转子导电槽楔和铁心、计及转子导电槽楔和大齿导条等三种情况下的大扰动低频振荡过程进行对比，如图8(c)所示。三种情况下的功角最大幅值分别为44.93°、42.36°、41.55°。从图中可以看出，仅计转子导电槽楔作用时系统功角的振荡幅值与转子导电槽楔和铁心共同作用、转子导电槽楔和大齿导条共同作用时均较为接近。

综上所述可以看出，转子大齿导条单独作用与大齿导条和其它两种转子阻尼结构分别作用时的大扰动低频振荡过程均相差较大；转子铁心单独作用与转子铁心和其它两种转子阻尼结构分别作用时的大扰动低频振荡过程也相差较大；而转子槽楔单独作用、转子槽楔与大齿导条共同作用、转子槽楔与铁心共同作用时的大扰动低频振荡过程则相差较小，因而可以得出在转子各部分结构阻尼相互作用时转子槽楔仍然起主要作用。

为了进一步分析转子各部分阻尼结构在大扰动低频振荡过程中的作用，将扰动过程中各阻尼结构中的阻尼电流折合到d、q轴，分别得出在d轴的阻尼电流ID和q轴阻尼电流IQ，对比各部分阻尼电流的大小。当三部分阻尼全计及时，计算得出其中电流如图9所示.从图中看出：转子槽楔的直轴阻尼电流分量远大于其它两种阻尼结构；而三部分阻尼的交轴阻尼电流分量相差不大，且转子槽楔中的电流更大一些。总体来看，转子槽楔中的阻尼电流最大，而大齿导条中的阻尼电流最小，阻尼电流越大，其产生的磁场与定子磁场之间产生电磁力越大，发电机转速和功角就越易趋于稳定。

图8 转子各部分阻尼单独作用与共同作用功角曲线对比Fig.8 Comparison of power angle curves under separately and interaction effect of damping structures

2.4 转子不同槽楔材料对大扰动低频振荡的影响

通常情况下，不同容量和型号的汽轮发电机转子槽楔的材料也不相同，主要有不锈钢槽楔、铝合金槽楔和铜基合金槽楔等几种类型，这些槽楔材料的磁导率基本相同而电导率却相差较大。由表2可知，铝合金的电导率约为不锈钢的12倍。为了研究转子不同槽楔材料对大扰动低频振荡的影响，本节对比分析了转子槽楔采用不锈钢和铝合金时，转子槽楔单独作用、转子槽楔与铁心共同作用、转子槽楔与大齿导条共同作用以及转子阻尼全部作用四种情况下，两种不同槽楔材料对发电机的大扰动低频振荡的影响，结果如图10所示。

图9 三部分阻尼全计及时各阻尼结构中的电流Fig.9 Currents in three component of rotor damping structure

从图10中可以看出，四种情况下转子槽楔采用不锈钢材料时功角的摆动幅值明显大于铝合金材料。这是因为系统大扰动导致发电机的输入和输出功率失去平衡，从而引起转速偏离同步速，这种情况下同步旋转磁场切割转子绕组产生感应电流，该电流产生的磁场与同步旋转磁场之间会产生电磁力，电磁力越大发电机转速越易趋于稳定，功角也就越易趋于稳定。而该电磁力的大小主要取决于转子绕组上感应电流的大小，该电流的大小与材料的电导率成正比。

为了分析转子槽楔材料对阻尼电流大小影响，分别计算转子槽楔采用铝合金和不锈钢时时，槽楔中阻尼电流的大小，结果如图11所示。从图中可以看出，转子槽楔采用铝合金时的直轴阻尼电流分量和交轴阻尼电流分量均大于采用不锈钢槽楔时的电流。因此，铝合金槽楔对于大扰动后低频振荡的抑制作用要强于不锈钢槽楔。

图10 转子槽楔采用不同材料时的大扰动功角特性曲线Fig.10 Power angle curves after big disturbance under the effect of different material of slot wedge

图11 不同转子槽楔材料低频振荡过程中槽楔阻尼电流Fig.11 Damping currents of slot wedge with different rotor wedge material during low frequency oscillation

3 结 论

1)通过对汽轮发电机转子阻尼作用计及与否时的大扰动低频振荡过程进行对比分析，得出转子阻尼结构的作用不仅可以抑制大扰动后功角的最大摆动幅值，而且可以有效减小大扰动低频振荡过程的衰减时间常数。

2)通过对汽轮发电机转子各部分阻尼单独作用时的大扰动低频振荡过程进行对比分析，得出转子导电槽楔单独作用时的阻尼比最大，且衰减时间常数最小；而大齿导条单独作用时的阻尼比最小，且衰减时间常数最大；在转子各部分阻尼共同作用时，转子槽楔仍然起主要作用。

3)通过对汽轮发电机转子槽楔材料采用铝合金和不锈钢时的大扰动低频振荡过程进行对比分析，得出四种情况下转子槽楔采用不锈钢时的功角振荡幅值明显大于其采用铝合金时的振荡幅值，采用电导率较大的转子槽楔材料可以有效抑制发电机大扰动低频振荡过程中的功角幅值。

[1] 陈恩泽，刘涤尘，廖清芬，等．多重扰动下的跨区电网低频振荡研究[J]．电工技术学报，2014，29(2)：290-295． CHEN Enze,LIU Dichen,LIAO Qingfen,et al.Research on low frequency oscillation of interconnected power grid based on multiple disturbances[J].Transactions of China Electro-technical Society,2014,29(2): 290-295.

[2] 耿博,姜睿,罗贵明.基于最小二乘法的最优自适应电力系统稳定器[J].电机与控制学报，2007，11(5)： 512-516. GENG Bo,JIANG Rui,LUO Guiming.Optmial adaptive power system stabilizer based on least-squares algorithm [J].Electric Machines and Control，2007，11(5)：512-516.

[3] 宋墩文，杨学涛，丁巧林，等．大规模互联电网低频振荡分析与控制方法综述[J]．中国电机工程学报，2011，35(10)：23-27． SONG Dunwen,YANG Xuetao,DING Qiaolin,et al.A survey on analysis on low frequency oscillation in large-scale interconnected power grid and its control measures[J].Proceedings of the CSEE，2011，35(10)：23-27．

[4] HAQUE M H．Evaluation of first swing stability of a large power system with various FACTS devices [J].IEEE Trans.Power Syst,2008,23(3): 1144-1151.

[5] 李伟力，孙佳慧，孙宏丽．汽轮发电机稳态与负序工况下转子涡流损耗计算和温度场分析[J]．电工技术学报，2012，27(9)：174-182． LI Weili,SUN Jiahui,SUN Hongli.Calculation and analysis of eddy loss and temperature field in rotor of synchronous generator under steady state and negative sequence[J].Transactions of China Electro-technical Society,2012,27(9): 174-182．

[6] 许国瑞，刘晓芳，罗应立，等．汽轮发电机转子阻尼系统对第一摆稳定性影响的仿真计算研究[J]．中国电机工程学报，2015，35(1)：214-222． XU Guorui，LIU Xiaofang，LUO Yingli,et al.Simulation study of the first swing stability affected by rotor damping systems of turbine generators[J].Proceedings of the CSEE，2015，35(1): 214-222．

[7] SHAHROKH S,JAFAR S．Damping of low frequency oscillations of multi-machine multi-UPFC power systems based on adaptive input-output feedback linearization control[J]．IEEE Transactions on Power Systems,2012,27(4): 1831-1839.

[8] DJORDJE M D,MARKO V J．An improved method of damping of generator oscillations[J]．IEEE Transactions on Energy Convers.,1999,14(4):1624-1629.

[9] 薛禹胜，郝思鹏，刘俊勇，等．关于低频振荡分析方法的评述[J].电力系统自动化，2009，33(3)：1-8. XUE Yusheng,HAO Sipeng,LIU Junyong,et al.A review of analysis methods for low-frequency oscillations[J] Automation of Electric Systems，2009，33(3)：1-8．

[10] 徐英新，王西田，杨帆，等．同步发电机阻尼绕组和磁路饱和对低频振荡阻尼的影响[J]．电力自动化设备，2007，27(5)：28-31 XU Yingxin,WANG Xitian,YANG Fan,et al.Effect of synchronous machine damper windings and magnetic saturation on low-frequency oscillation damping [J].Electric Power Automation Equipment，2007，27(5)：28-35.

[11] 魏伟,杨艳.电力系统阻尼特性规律探索[J].电机与控制学报，2008，12(1)：34-37. WEI Wei,YANG Yan.Researches on damping characteristics of electric power systems [J].Electric Machines and Control，2008，12(1)：34-37.

[12] CANAY I M．Determination of the model parameters of machines from the reactance operators xd(p),xq(p) [J].IEEE Trans.Energy Convers.1993,8(2): 272-279.

[13] GAO Jingde,ZHANG Linzheng,WANG Xiangheng．AC machine system:mathematical model and parameters,analysis,and system performance[M].Springer- Verlagand Tsinghua University Press,Beijing,2009: 58-266.

[14] 吴跨宇，竺士章.发电机励磁系统调差对 PSS 参数整定的影响与对策[J].电力自动化设备，2010，30(9)：67-71． WU Kuayu,ZHU Shizhang.Effect of reactive compensation for generator excitation system on PSS parameter setting and solution [J].Electric Power Automation Equipment，2010，30(9)：67-71．

[15] 高莲莲,梁艳萍.双屏蔽电机定子端部漏抗计算及其影响分析[J].电机与控制学报，2015，19(5)：53-57. GAO Lianlian， LIANG Yanping.Calculation and analysis of stator end leakage reactance of double canned motor [J].Electric Machines and Control，2015，19(5)：53-57.

[16] 罗应立，胡笳，刘晓芳，等．面向系统动态分析的场路网耦合时步有限元模型[J]．中国电机工程学报，2009，29(33)：102-110. LUO Yingli,HU Jia,LIU Xiaofang,et al.Field-circuit-network coupled time-step finite element model for power system dynamic analysis[J].Proceedings of the CSEE,2009,29(33):102-110.

[17] SASIC M,LIOYD B,ELEZ A．Finite element analysis of turbine generator rotor winding shorted turns[J],IEEE Trans.Energy Convers.2012,27(4):930-937.

[18] XIALDONG L,ELSERAFI A M,FARIED S O．Application of the finite element method for the determination of the parameters representing the cross magnetizing in saturated synchronous machines [J].IEEE Trans.Energy Convers.,2010,25 (1): 71-79.

[19] IBRAHIM M，PILLAY P．Core loss prediction in electrical machine laminations considering skin effect and minor hysteresis loops[J]．IEEE Trans.on Industry Application，2013,PP(99): 2681-2686.

[20] STURGESS J P,ZHU M,MACDONALD D C.Finite-element simulation of a generator on load after a three-phase fault [J].IEEE Trans.Energy Convers.1992,7(4): 787-791.

[21] XU Guorui,LIU Xiaofang,KANG Jinping,et al.The influence of turbine generator rotor damping structure and material on first swing stability [J].Electric Power Systems Research,2015,124: 181-189.

Influenceofrotordampingstructureofturbinegeneratorsonlowfrequencyoscillationunderlargedisturbance

XU Guo-rui1， LI Jin-xiang2， FU Yong-qi1， HU Jia3， SUN Yu-tian2， LIU Xiao-fang1

(1.School of Electrical and Electronic Engineering,North China Electric Power University,Beijing 102206,China; 2.State Key Laboratory of Hydropower Equipment (Harbin Institute of Large Electrical Machinery),Harbin 150040,China; 3.China Power International Holding Ltd,Beijing 100080,China)

It aims to study the effect of rotor damping structure which contains damping bars,the rotor iron core and rotor slot wedges on low frequency oscillation (LFO) under large disturbance.Firstly,the time stepping finite element model of turbine generator was built to study the effect of rotor damping structure on LFO and the model was tested by the experiment of 7.5 kW model machine.Then,the influence of rotor damping on LFO under large disturbance was studied under the individual and combined effect of three components of rotor damping structures.Finally,the influence of different rotor slot wedge material on LFO was studied.The results show that the rotor damping structure can suppress LFO under large disturbance.The rotor slot wedge plays a more vital role during LFO after large disturbance and the aluminum alloy slot wedge has a better suppression effect than that made of stainless steel.

rotor damping system; large disturbance; low frequency oscillation; turbine generator；time stepping finite element model

(编辑：贾志超)

2016-01-01

国家自然科学基金(51507059，51477049)；中央高校基本科研业务费专项资金资助 (2015QN03)

许国瑞(1986—)，男，博士，研究方向为同步发电机模型、参数及机网协调运行； 李金香(1965—)，女，硕士，高级工程师，研究方向为电机磁场理论研究与计算、电机瞬变过程分析与计算； 付永旗(1992—)，男，硕士，研究方向为同步发电机大扰动特性； 胡 笳(1982—)，男，博士，研究方向为同步发电机动态扰动特性； 孙玉田(1963—)，男，博士，教授级高工，研究方向为电机电磁场、电机及系统动态分析； 刘晓芳(1961—)，女，学士，教授，研究方向为大型电机非正常运行及暂稳态特性。

许国瑞

10.15938/j.emc.2017.08.002

TM 302

:A

:1007-449X(2017)08-0009-09