基于广义等高线的灰色波形预测模型及其应用

陈彦晖，刘 斌

(上海海事大学经济管理学院，上海 201306)

基于广义等高线的灰色波形预测模型及其应用

陈彦晖，刘 斌

(上海海事大学经济管理学院，上海 201306)

本文针对波动性上升或下降的时间序列,提出了一类基于广义等高线的灰色波形预测模型。该模型通过拟合带时间趋势项的最小二乘估计确定等高线斜率，并基于此斜率在原始数据序列最小值和最大值之间选取一系列平行直线作为广义等高线，进而对等高时刻序列各元素横坐标进行GM(1,1)建模和预测。通过对我国民航客运量及近期原油价格的预测对模型进行检验，本文得出基于广义等高线的灰色波形预测模型能够实现对波动性上升和下降的时间序列的预测，并提高了灰色波形预测模型预测此类数据的准确性。此外，由于灰色波形预测模型所需样本量较小，本文提出的模型有助于对新兴事物发展变化的预测。

灰色波形预测；广义等高线；民航客运量；原油价格

1 引言

灰色系统预测是灰色系统理论研究中的一个重要领域，其主要方法是使用GM(1,N)模型或其扩展形式对时间序列的变化规律进行建模，从而对时间序列未来的发展趋势进行预测。由于灰色系统预测模型具有建模所需数据小、不必考虑数据的分布等特点[1-3]，因此受到了众多学者的青睐。例如吴振信和石佳[4]利用GM(1,1)模型预测了北京市的碳排放强度；花玲和谢乃明[5]考虑了政策冲击的影响并利用灰色GM(1,1)模型对中国能源消费总量和单位GDP能耗进行了模拟和预测；Wei Jiuchang和 Zhou Lei等[6]运用GM(1,1)模型预测了中国大陆高速交通事故，铁路交通事故，矿山生产事故等生产事故的伤亡人数；钱吴永和党耀国等人[7]构建了含时间幂次项的灰色GM(1,1,t～α)模型,并对某沿海高速的软土地基沉降进行了拟合与预测；刘解放和刘思峰等人[8]提出了反向累加NHGM(1,1,k)模型，并对在研武器装备的可靠度进行预测；杨保华和赵金帅[9]运用离散灰色幂模型对中国网络购物人数进行预测。

然而由于GM(1,N)模型只适用于单调变化的时间序列[1-2]，研究者根据数据的变化规律又对GM(1,N)模型进行了改进。对于波动性的时间序列，丰景春和杨建基[10]提出了GM(1,1,sinω)模型，钱吴永和党耀国[11]提出了GM(1,1)振荡序列模型。前者用一组具有灰频率参数的正弦项表示时间序列的摆动部分，建立一个含有灰频率参数正弦项的一阶灰差分方程，从而实现对具有波动性质的时间序列的预测，而后者通过加速平移变换将振荡序列变为单调增加序列，然后再对加速平移变换后的序列进行加权均值生成变换,再以加权均值生成变换得到的序列建立GM(1,1)模型进行预测。但是GM(1,1,sinω)模型和GM(1,1)振荡序列模型的应用研究却十分局限，只有郭立春和吴伟等[12]应用GM(1,1,sinω)模型预测沈阳市肾综合征出血热的流行趋势，而GM(1,1)振荡序列模型也只是通过算例进行了有效性检验。这两种模型均使用了精密了的数学理论，因此在应用方面较难被人掌握。此外，这两种模型仅适用于波动序列，对于具备增长趋势或下降趋势的波动序列的预测问题，这两种模型依旧未能解决。

灰色波形预测就是灰色系统理论中针对周期性波动序列而提出的一种预测方法，它以数据序列波动图形为基础进行预测，因而又称灰色图形预测或灰色拓扑预测。它从给定的一系列阈值出发，建立GM(1,1)群，利用多个GM(1,1)模型来对整个图形的发展趋势进行预测。该方法对频频波动且摆动幅度较大的时间序列的预测取得了良好的效果，如文献[13-15]等。灰色波形预测同时还具备灰色预测模型的一般优势，即运用较少的样本数据对时间序列进行中长期预测。如樊玮和张沂华等人[15]采用了36个数据来建立预测模型，10个数据来检测模型的预测效果。此外，灰色波形预测建模直观，不涉及精密的数学理论，在运用上较GM(1,1, sinω)模型和GM(1,1)振荡模型易被掌握。但是，对灰色波形预测模型的改进研究依然十分有限，过往研究中只有Wan Qin等[16]和陈彦晖[17]对于波动幅度不规律的时间序列提出了灰色波形预测模型的改进方法。然而过往研究所使用的数据在波动时并无明显的上升或下降趋势，因此针对随时间增长的周期性波动序列需要对现有灰色波形预测模型做进一步改进。

本文针对波动性上升或下降的时间序列提出了基于广义等高线的灰色波形预测模型。本文的创新点在于拓展了等高线的概念并提出通过拟合一个含简单趋势参数的普通最小二乘估计确定广义等高线的斜率。在广义等高线截距的确定上，提出首先通过时间序列样本区间内的最大值和最小值确定最高一条和最低一条广义等高线，然后采取等间距的方式确定其余若干条广义等高线。在应用分析中，本文选用我国民航客运量的月数据和近期原油价格的日数据对模型进行检验。

2 模型构建

灰色波形预测是对一个变化不规则的数据序列的整体发展进行预测，通过对等高线与数据序列波动图形折线的交点坐标进行GM(1,1)建模，一般在系统波动比较频繁的情况下应用。灰色波形预测模型主要通过等高线选取，确定等高时刻序列，对等高时刻序列进行GM(1,1) 建模三个步骤完成[1]。其中，等高线的选取及等高时刻序列的确定也可以看作是对数据图形信息的抓取过程。它们的原理就是得到等高线与数据图形交点的信息，并找到其规律性。

2.1 选取广义等高线

原有的灰色波形预测模型选取水平的等高线，该方法对周期性水平波动的数据具有较好的预测效果。然而，许多经济数据呈现上升性波动的态势，如果要应用灰色波形预测模型对预测该类数据的未来发展趋势，就需要考虑数据的时间增长趋势，而水平的等高线，无法刻画数据的时间增长趋势。因此对于波动性上升的数据，需要设置广义的等高线来抓取数据图形信息(如图1所示)。

定义1:设原始序列为：X=(x(1),x(2),…,x(n))，则称

xk=x(k)+(t-k)[x(k+1)-x(k)]

为序列X的第k～(k+1)段线段。其中k∈[1,n]且为整数，t∈[k,k+1]为一未知参数。

称：

{xk=x(k)+(t-k)[x(k+1)-x(k)]|k=1,2,…,n-1}

为序列X的折线，仍记为X，即：

X={xk=x(k)+(t-k)[x(k+1)-x(k)]|k=1,2,…,n-1}

定义2(广义等高线的斜率)：设原始序列为：X=(x(1),x(2),…,x(n))，拟合一个含时间趋势参数的线性回归方程：

x(k)=a0+a1k+εt

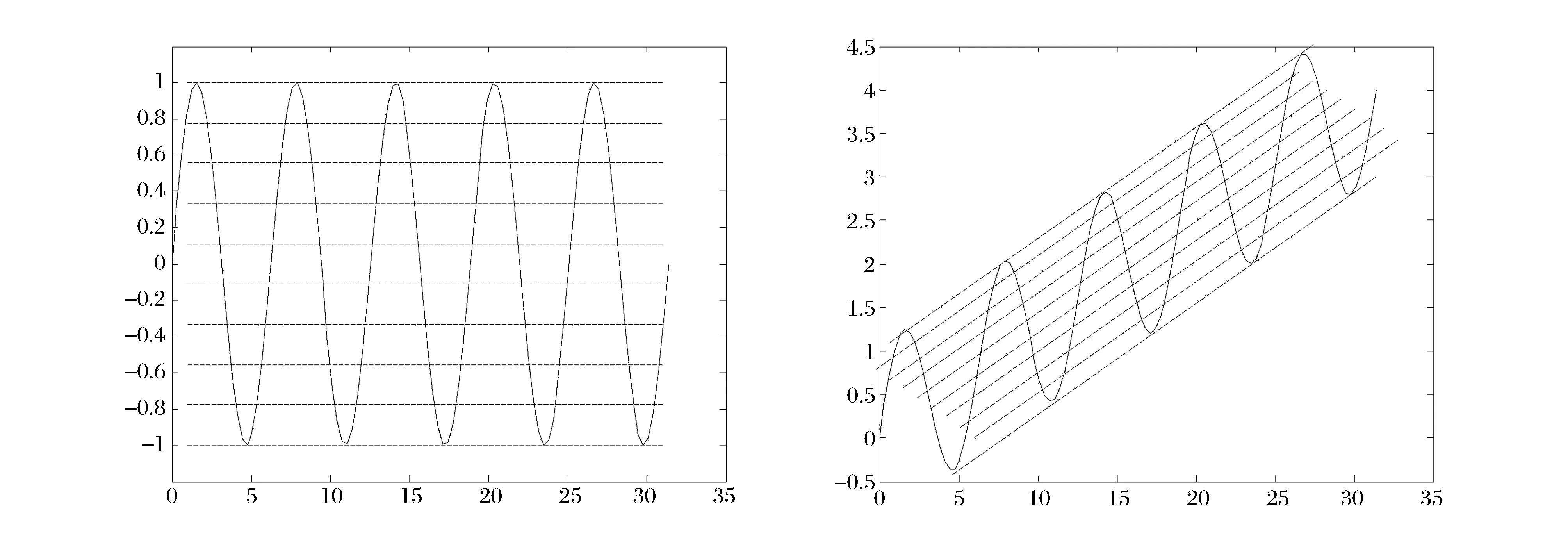
图1 无时间趋势项和有时间趋势项的周期性波动序列

其中εk是白噪声过程，k∈[1,n]且为整数。则称a1为广义等高线的斜率。

定义3(广义等高线)：设原始序列的最大值最小值分别为x(i)和x(j)，且i≠j。

1o原始序列最低和最高一条等高线分别为ξ0=α0+a1k，ξs=αs+a1k，其中α0=x(i)-a1i，αs=x(j)-a1j。

2o令ξ1=α0+(αs-α0)/s+a1k，ξ2=α0+2(αs-α0)/s+a1k，……，ξs-1=α0+(s-1)(αs-α0)/s+a1k。则称(ξ0,ξ1,ξ2,…,ξs-1,ξs)所确定的斜线为原始数据的s+1条广义等高线。

2.2 确定广义等高时刻序列

确定等高时刻序列时应根据上节所确定的等高线，按时间先后顺序进行。

定义4(广义等高点)：称方程组

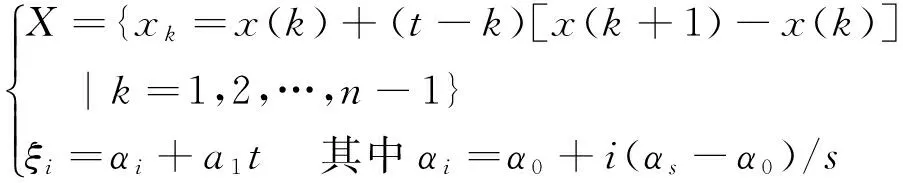
的解为(tl,x(tl))(l=1,2,……)为ξi-广义等高点。ξi-广义等高点是折线X与ξi-等高线的交点。

命题1：若X的第(k)～(k+1)段折线上有ξi-广义等高点，则其坐标为；

证明：第t～(t+1)段折线的方程为：

xk=x(k)+(t-k)[x(k+1)-x(k)]

联立

令

ξi(k)=αi+a1k，ξi(k+1)=αi+a1(k+1)

可得：

αi=ξi(k)-a1k，a1=ξi(k+1)-ξi(k)

代入联立方程组可解得X的第(k)～(k+1)段折线与ξi-广义等高线交点的横坐标为：

定义5(广义等高时刻序列)：设Xξi=(P1,P2,…,Pmi)为ξi-广义等高点序列，其中Pj位于第kj～(kj+1)段折线上，Pj点的坐标为：

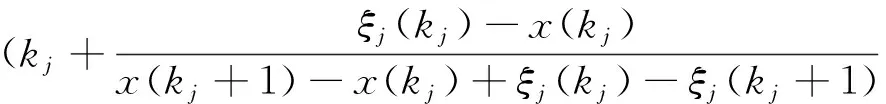
令：

j=1,2,…,m

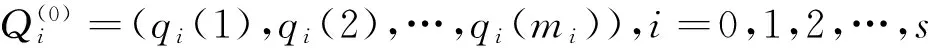
2.3 GM(1,1)建模与预测

GM(1,1)建模需要至少四个数据才能完成[18, 19]。因此，在灰色波形预测方法中，对4个及4个以上元素的等高时刻序列进行GM(1,1)建模。

命题2：设

为ξi等高时刻序列的GM(1,1)预测值。删去所有等高时刻序列中的无效预测时刻[1]，并将其余的预测值从小到大重新排序，设该序列为：

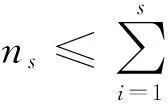
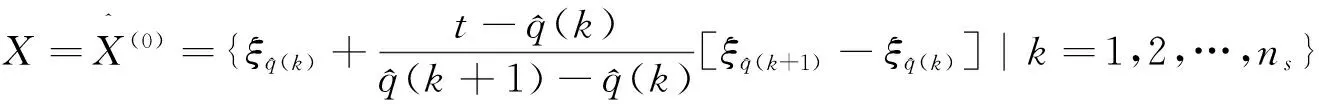
3 应用分析

3.1 对上升趋势预测：以民航客运量的预测为例

自上世纪90年代以来我国一直处于经济快速发展的阶段，民航运输客运量一直处于稳定增长的阶段，但由于季节性影响，这类数据呈现出波动性上涨的形态[20]。本文选取2011年1月到2015年2月我国民航客运量的月度数据进行实证检验。

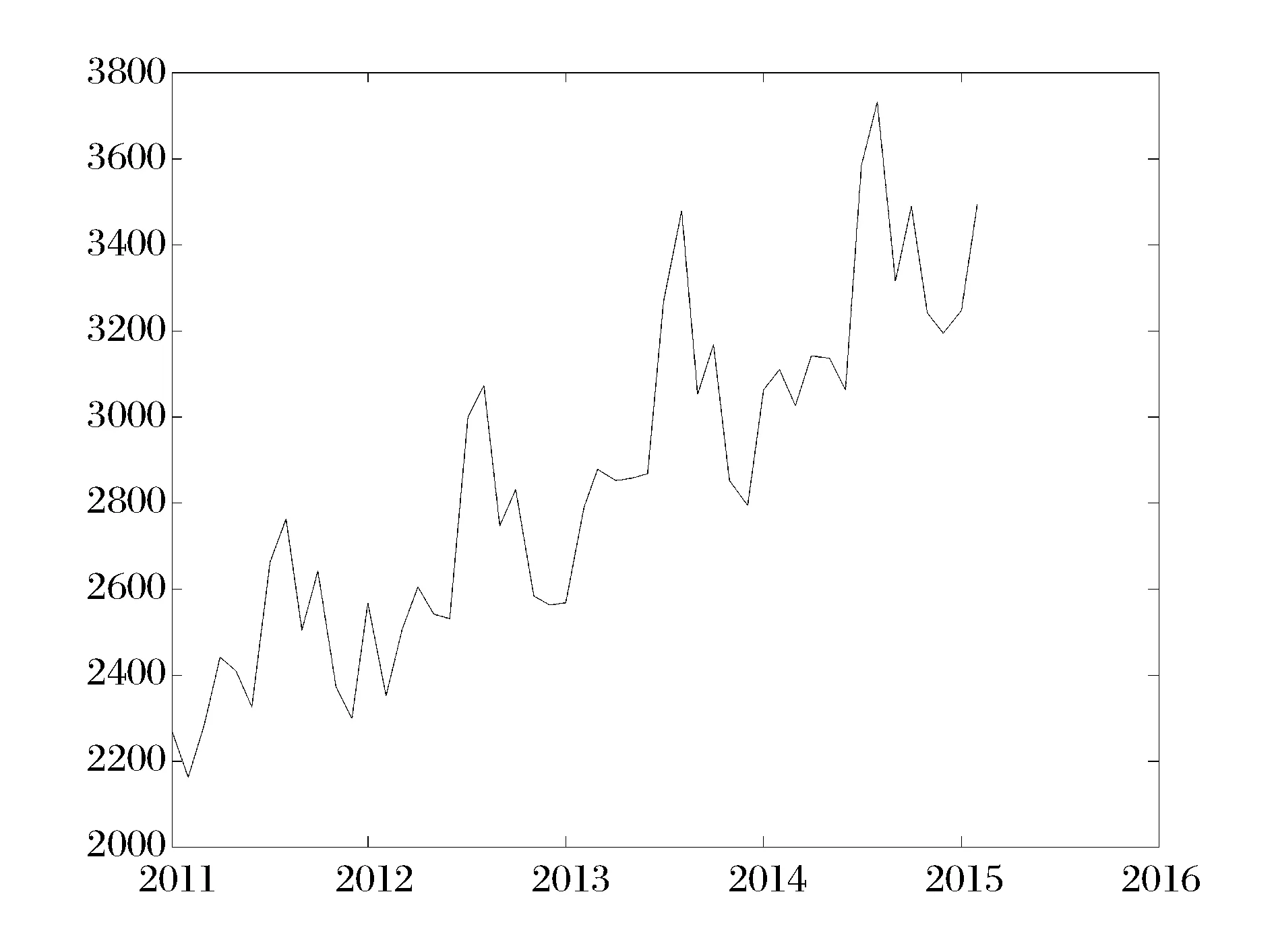
图2 2011年1月到2015年2月我国民航客运量的月数据

如图1所示，在此期间我国民航客运量呈现明显的季节性波动上升趋势，符合本文所提模型的使用条件。

本文将2011年1月到2015年2月共50个观测值分为样本内数据和样本外数据两部分，其中样本内数据36条(2011年1月到2013年12月)，用于确定等高线、等高时刻序列及进行GM(1,1)建模；样本外数据14条(2014年1月到2015年2月)，通过进行14步预测的方式，对我国民航客运量的月数据进行预测。此外，本文全部的实证检验均通过MatlabR2010a编程计算得到。

依据灰色波形预测方法的步骤，本节首先进行等高线的选取，当s=9时，民航客运量的10条等高线方程的斜率为22.25，常数项分别为(α0,α1,…,α9)=(2118.50，2190.22，2261.94，2333.66，2405.39，2477.11，2548.83，2620.55，2692.27，2763.99)。等高线的分布如图2所示。

图3 广义等高线选取(2011年1月到2013年12月)

由低到高确定十个等高时刻序列，分别如下：

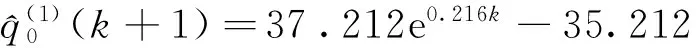
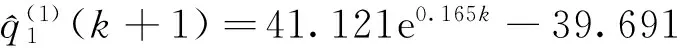
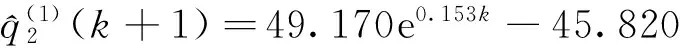
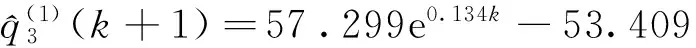
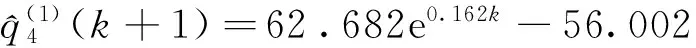
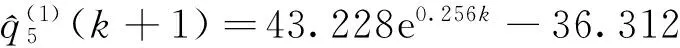
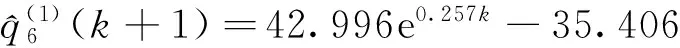
预测精度如表1所示。

3.2 对下降趋势预测：以近期原油价格的预测为例

自2014年下半年以来，由于投资者对全球经济放缓的担心，加之页岩油气的异军突起及欧佩克组织的未就减产达成一致意见，世界原油价格一直处于波动性下跌的走势[21]。2015年下半年以来，由于全球经济复苏低于预期，且受2015年冬天暖冬影响，美国原油库存迟迟难以消化[22]，这使得世界原油价格依然有下降趋势(如图4所示)。

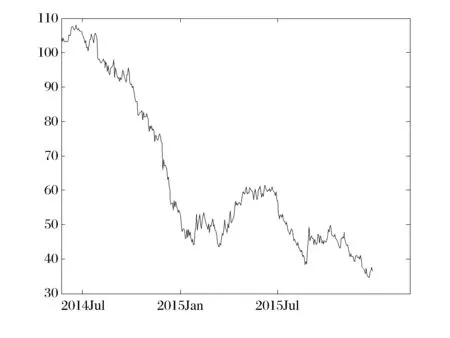
图4 2014年7月1日到2015年12月28日的WTI价格

为了验证基于广义等高线的灰色预测模型同样适用于波动性下降的时间序列数据，本节采用2014年7月以来的美国西德克萨斯轻质原油(WTI)进行测试。在测试过程中本文采取20步预测的方式进行预测。此外本节采取数据不断向前推移的方式进行了15组共计300个测试点。预测精度如表1所示。

3.3 预测结果比较

为了验证本文提出的模型的优越性，本文选用基于水平等高线的灰色波形预测模型作为对照模型，为了提高预测精度，本文在建立GM(1,1)模型群之前，采取参考文献[17]的方法对等高时刻序列进行筛选，仅对合格的等高时刻序列进行预测。此外，本文还选取去时间趋势的ARMA模型作为对照模型。在对预测精度的比较方面，本文选取了均方根误差(Root Mean Squared Error，RMSE)、泰尔不平等系数(Theil’s inequality coefficient，TIC)和平均绝对误差百分比(Mean Absolute Percentage Error，MAPE)对三种模型进行比较。三种模型对我国民航客运量月数据和近期原油价格的预测精度比较如表1所示。通过对MSE、TIC和MAPE的比较可以得出，基于广义等高线的灰色波形预测模型明显优于基于水平等高线的灰色波形预测模型。此外，基于广义等高线的灰色波形预测模型也优于去时间趋势项的ARMA模型。过往研究中，曾有学者使用季节调整的ARMA模型对民航客运量进行预测，由于实证研究得出对民航客运量预测时，季节调整项的阶数为12[20]，这也就意味着季节调整的ARMA模型需要至少40条样本内数据才能拟合参数。由此可见，灰色系统预测方法可基于较少的样本容量对事物的未来变化趋势进行预测的优势在灰色波形预测模型中也得到了体现。

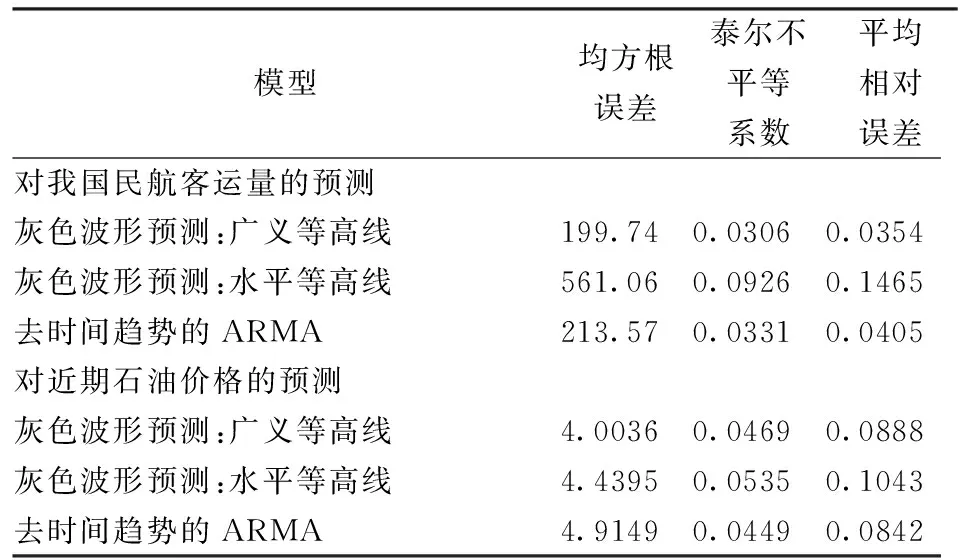
表1 预测精度比较

4 结语

针对波动性增长的时间序列的预测问题，本文通过引入时间趋势项，提出了基于广义等高线的灰色波形预测模型。本文通过拟合带时间趋势项的最小二乘估计确定广义等高线的斜率，通过选取原始序列最大值和最小值，确定最低一条和最高一条广义等高线的常数项，然后选取这两个常数项间的平均数作为其余s-1条广义等高线的常数项。最后，通过对我国民航客运量的预测进行实证检验，本文得出，在对具有增长趋势的波动性时间序列进行预测时，基于广义等高线的灰色波形预测模型预测结果优于原有的灰色波形预测模型预测结果，也优于去时间趋势的ARMA模型。此外，由于灰色波形预测模型预测时不需要像季节调整的ARMA模型一样需要大量的样本内数据才能确定模型参数，这对新兴事物的发展变化预测起到了积极的帮助作用。

[1] 刘思峰，党耀国，方志耕，等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2010.

[2] Liu Sifeng， Lin Yi. Grey systems: Theory and applications[M]. Berlin,Germang:Springer Science & Business Media, 2010.

[3] Deng Julong. Introduction to grey system theory[J]. The Journal of Grey System, 1989, 1(1): 1-24.

[4] 吴振信, 石佳. 基于STIRPAT和GM(1,1)模型的北京能源碳排放影响因素分析及趋势预测[J]. 中国管理科学, 2012,20(S2): 803-809.

[5] 花玲, 谢乃明. 政策冲击影响下中国能源消费预测分析及控制策略[J]. 中国管理科学, 2014,22(7): 18-25.

[6] Wei Jiuchang, Zhou Lei, Wang Fangfei, et al. Work safety evaluation in Mainland China using grey theory[J]. Applied Mathematical Modelling, 2015, 39(2): 924-933.

[7] 钱吴永, 党耀国, 刘思峰. 含时间幂次项的灰色GM(1,1,t～α)模型及其应用[J]. 系统工程理论与实践, 2012,32(10): 2247-2252.

[8] 刘解放, 刘思峰, 吴利丰, 等. 分数阶反向累加NHGM(1,1,k)模型及其应用研究[J]. 系统工程理论与实践, 2016,36(4): 1033-1041.

[9] 杨保华, 赵金帅. 优化离散灰色幂模型及其应用[J]. 中国管理科学, 2016,24(2): 162-168.

[10] 丰景春，杨建基. 水利水电工程项目质量控制系统灰色摆动模型[J]. 河海大学学报(自然科学版), 1999, 27(5): 57-62.

[11] 钱吴永，党耀国. 基于振荡序列的GM(1,1)模型[J]. 系统工程理论与实践, 2009, 29(3): 149-154.

[12] 郭立春，吴伟，郭军巧，等. 应用灰色摆动模型预测沈阳市肾综合征出血热的流行趋势[J]. 中国医科大学学报, 2008, 37(6): 839-842.

[13] 陈可嘉，季平，刘思峰，等. 灰色波形预测在经济周期波动中的应用[C].2006年灰色系统理论及其应用学术会议，中国北京，2006年10月.

[14] 栾珺. 基于灰色理论的上证指数预测研究[J]. 知识经济, 2009, (13): 23.

[15] 樊玮，张沂华，慈祥，等. 基于灰色拓扑预测的航班订座需求预测模型[C].2010 Internation at Conference on Services Science,Management and Engineering,中国天津，2010年12月26日.

[16] Wan Qin，Wei Yong，Yang Xiongqiong. Research on grey wave forecasting model[M].Liu Sifeng,Lin Yi.Advances ingrey systems research,Berlin-Heidelberh:Springer-Verlay,2010.

[17] 陈彦晖. 波罗的海干散货指数预测的非等间隔灰色波形预测方法[J]. 大连海事大学学报, 2015,41(4): 96-101.

[18] 刘思峰，党耀国，方志耕，等. 灰色系统理论及其应用[M].北京：科学出版社, 2008.

[19] 郑彦. 民航客运量季节调整实证研究[J]. 山东理工大学学报(自然科学版), 2011, (01): 64-67+71.

[20] 徐建山, 朱颖超,孙依敏. 国际油价下跌原因辨析[J]. 国际经济合作, 2015,(2): 61-65.

[21] 大连商品交易所. 原油简评：担心暖冬油品库存高企，国际油价继续下跌[Z].(2015-10-27) http://www.dce.com.cn/portal/info?cid=1329986114100&iid=[2016-01-04].1445905468100&type=CMS.NEWS.

Grey Wave Forecasting Model with Generalized Contour Lines and its Application

CHEN Yan-hui, LIU Bin

(School of Economics and Management Shanghai Maritime University, Shanghai 201306,China)

In this paper, a modified grey wave forecasting model with generalized contour lines is proposed to forecast time series which is increasing (or decreasing) and fluctuating with time. The modified model identifies the slope of contour lines through a linear regression model with time trend and estimates the regression model with ordinary least square method. And then a set of parallel lines between the minimum and maximum values of original data series are chosen as the generalized contour lines. In the last step, GM(1,1) models are established based on the elements in generalized contour time sequences. In the empirical analysis, the proposed model is used to forecast Chinese airline passenger volume, which fluctuates with increasing trend and crude oil price, which fluctuates with decreasing trend in the past several months. The result indicates that grey wave forecasting model with generalized contour lines can improve the accuracy of grey wave forecasting model with horizontal contour lines. Also it is useful to forecast the development of emerging things, since it just uses relatively few sample data.

grey wave forecasting; generalized contour lines; airline passenger volume; crude oil price

1003-207(2017)08-0134-06

10.16381/j.cnki.issn1003-207x.2017.08.014

2015-06-29；

2016-01-05

国家自然科学基金资助项目(71571117,71201054);国家社会科学基金资助项目(11BJY110);上海市基础研究重点项目(15590501800)

陈彦晖(1984-)，女(汉族)，山西临县人，上海海事大学经济管理学院讲师，研究方向：数量经济、预测方法、管理科学与工程，E-mail:chenyh@shmtu.edu.cn.

F224

A