复合系统的动态协同演化分析——以保险、信货与股票金融复合系统为例

任 腾，周忠宝

(1. 中南林业科技大学物流与交通学院，湖南 长沙 410018；2. 湖南大学工商管理学院，湖南 长沙 410082)

复合系统的动态协同演化分析
——以保险、信货与股票金融复合系统为例

任 腾1，周忠宝2

(1. 中南林业科技大学物流与交通学院，湖南 长沙 410018；2. 湖南大学工商管理学院，湖南 长沙 410082)

从系统论的视角出发，在保险、信贷与股票市场相互作用理论分析的基础上，将协同理论与基于动态邻居和局部搜索的粒子群算法(DNLPSO)相结合，构建了保险、信贷与股票金融复合系统动态协同演化模型，并运用此模型构建复合系统有序度计算公式，然后利用DNLPSO算法对模型进行求解，并对模型进行稳定性分析。模型既考虑了系统之间的非线性关系，同时加入结构变化参数和滞后参数以描述重大事件和系统的滞后影响。基于省际面板数据，利用该模型对我国2004-2013年保险、信贷与股票市场复合系统的协同演化现状进行了实证研究。实证结果表明，该模型能够很好地反映了各子系统的滞后项和2008年金融危机对复合系统协同演化进程的影响，完整地体现了该复合系统的局部竞争合作关系和长期趋于稳定性的整体特征，为三复合系统协同演化分析提供了一个研究范式。

动态协同演化；稳定性分析；DNLPSO算法；复合系统

1 引言

目前，在社会各领域都广泛存在着由三个或三个以上具有内在联系的子系统共同组成的复合系统，如由保险、信贷、股票组成的金融复合系统，由生态、经济、社会组成的生态经济复合系统。以本文的研究对象为例，作为金融市场的重要组成部分，保险、信贷与股票市场三者之间具有各自独特的经济作用却又彼此关联。首先，保险市场的风险补偿和转移功能为金融机构管理和控制自然风险提供了途径，进而有助于信贷市场规模的扩张。同时完善的银行信贷体系所具备的有效结算能力为保险市场的发展提供了保障。其次，股票市场为保险公司提供了融资平台，有助于保险公司规模的扩大，促进保险市场的快速发展。与之对应的是，保险市场中寿险、养老保险等人身保险产品的发展将减少居民预防性储蓄，使得更多闲置资金流入股票市场，有利于股票市场的发展。最后，股票市场投资环境的恶化将使得居民闲置资金更多转化为储蓄，从而有利于银行信贷业务的发展。

另一方面，信贷市场的本质是将储蓄资金从盈余单位向赤字单位有效的转移，而部分人寿保险产品也具有这种资本配置和转移功能，两者相互竞争。此外，股票市场的集聚资金和提高资金配置效率的经济作用对信贷市场的发展有一定的抑制作用。综上可知，保险、信贷和股票市场都是金融市场的重要组成部分，三者之间既有统一的一面，也有对立的一面，同时存在合作与竞争，三者之间的合作与竞争是金融协同形成的关键，同时也是金融市场发展的内在动力，深入探讨三大市场的相互作用是扩大金融协同效应的客观前提。在不完善的金融市场背景下，深入研究我国保险、信贷与股票市场之间的协同演化现状对于政府改革金融市场具有重大的指导意义。

然而，当前针对保险、信贷与股票市场竞争合作关系的研究鲜见，已有研究主要集中于探讨三者在经济增长进程中的竞争合作关系[1-4]，而将三者作为独立系统并对其协同演化进程进行刻画的研究尚处于空白。进一步，当前对于复合系统协同演化的相关研究大多集中在企业系统内部之间的相互作用关系和协同演化机理[5-10]，其基本思想是将企业系统抽象为两个或者三个序参量，结合协同论学基本理论对企业系统进行定量描述。关于彼此独立复合系统的协同演化研究很少，且主要集中于两系统的协同演化[11-14]，真正运用协同演化模型把三个及以上具有内在联系的复合系统联合研究的文献更为少见。范斐等[15]构建了社会、经济与资源环境三系统的协同演化模型，崔强等[16]构建了包含铁路、公路、水路和航空的交通运输复合系统的动态演化方程，但上述两个文献存在如下不足：一是对于数据的要求为时间序列，导致虽然数据收集难度不大，但因为数据样本较小使得测算精度较低；二是基于单一的AHP方法建立的有序度测算模型大多只关注了基于个人偏好的决策者评分，而往往忽视了相关数据呈现的特征；三是由于有序度的相关数据具有时间序列的基本属性，而保险、信贷与股票市场三者间的相互作用关系是否具有滞后性这一问题在现有研究中鲜有涉及；四是现有模型无法模拟仿真有关重要事项对协同演化的影响。在现实生活中，保险、信贷与股票市场之间的相互影响时常存在滞后性，而有关重要的社会事件、经济事件都将影响金融市场的运行过程。因此，在分析保险、信贷和股票市场三者之间的协同演化过程时，须考虑三者之间相互作用的滞后性以及重要社会事件、经济事件对演化过程的影响。

基于上述分析，本文主要从理论层面与实证层面进行试探性的创新。理论层面的贡献在于：首先，在面板数据的条件下，利用DEAHP方法构建了系统的有序度模型，从而使得指标权重兼顾了主观偏好和数据特征的重要性。其次，充分考虑系统之间的滞后影响和重大经济事件的影响，建立了由保险、信贷和股票市场三者共同组成的三复合系统协同演化模型，在对该模型进行稳定性分析的基础上，结合DNLSPO算法给出了模型参数求解方法。一方面，该模型既考虑了系统间相互影响的时滞性，又引入了结构参数，有助于宏观经济政策、外部冲击时间对复合系统的影响；另一方面，该模型不仅适用于时间序列，亦可应用于面板数据，拓展了动态演化模型的适用范围。实证层面的贡献在于：利用我国各省区2004-2013年间省际面板数据建模，对保险、信贷与股票系统的协同演化现状进行了实证研究，分析了三者之间的相互作用、长期稳定性及2008年金融危机对复合系统协同演化进程的影响。

全文结构安排如下：第二部分回顾协同学基本理论，并基于DEAHP方法构建有序度分析模型；第三部分构建由保险、信贷和股票三者共同组成的三复合系统协同演化模型，对模型整体进行稳定性分析，并给出相应求解方法；第四部分为实证研究与分析；第五部分总结全文。

2 协同学基本理论与有序度模型

2.1 协同学的基本理论

协同学是研究协同系统由无序状态到有序状态的演化过程、演化规律的一种交叉型综合学科，是由联邦德国理论物理学家哈肯于20世纪70年代初创立[17]。所谓协同，是指为了实现符合系统的总目标复合系统内部各个子系统之间的相互协作、相互作用的现象。而协同学则是对复合系统在内部子系统相互作用和外参量的驱动力共同作用下，达到系统有序的状态过程中所需的演化规律、临界条件。在研究中，学者们用一组状态参量来描述复合系统的协同状态，当系统在协同演化过程中接近于从量变到发生质变的临界点时吗，变化较慢的状态参量会出现数量较少的现象，而这种变化较慢的状态参量一般被称为序参量。与之对应的，变化速度加快、数量较多的状态参量则受序参量的支配和影响，最终被其消除。作为协同学中最基础、最经典的原理，这样的演化机理被命名为支配原理。

有上述论述可知，协同学是研究复合系统由无序状态到有序状态的演化过程、演化规律。对于社会进步和经济发展过程中出现的系统系统的协同进化过程是指复合系统与环境产生物质、能量和信息的交流，历经诞生、成长、成熟、衰退、死亡的进化过程，最终形成某种发展水平的均衡状态。[18]由于它们的演化轨迹属于S型曲线，因此可运用经典的Logistic增长模型对复合系统的协同进化过程进行描述刻画，如式(1)所示：

(1)

其中，X为复合系统的序参量，α为复合系统的增殖系数，而方程右边X为动态因子，(1-X)则为减速因子。

2.2 复合系统的有序度分析

设变量ui(i=1,2,3)为保险系统F1、信贷系统F2与股票系统F3的序参量，uij为第i个序参量的第j个指标，其值用Xij(j=1,2,…,n)表示，αij,βij则分别为系统序参量的上限值和下限值。据此，保险、信贷与股票市场三个子系统对复合系统有序的贡献系数uij可由(2)表示：

uij=(Xij-βij)/(αij-βij)

(2)

uij=(αij-Xij)/(αij-βij)

(3)

其中，式(2)适用于效益型指标，式(3)适用于成本型指标；uij则为变量对子系统Fi的贡献大小。据此，上式构造的贡献系数呈现以下特征：uij将反映各指标达到目标的满意程度，uij在趋近0时为完全不满意状态，而uij趋近1为完全满意，因此有0≤uij≤1。同时，因为保险、信贷和股市市场是三个持续相互作用的子系统，因此它们内部各指标对复合系统整体序参量的总贡献则可以运用加权集成的方式来表示。本文拟运用线性加权的方法，具体如下：

(4)

式(4)中，ui为子系统对总系统有序度的贡献，λij为各个参序量的权重。

现有研究中关于权重的确定已有多种成熟的理论方法，其中DEA方法注重对每一个决策单元进行优化，而层次分析法则偏向于注重决策者对于不同评价指标的偏好。因此，近年来将上述两种方法进行结合进行权重的方法已成为决策领域形成的一个共识。

近年来，Ramanathan[18]最早建立了一种将DEA方法和AHP方法相结合的DEAHP方法。然而，Wang Yingming等[20]指出该方法在比较矩阵不连续的情况下不能保证得到合理的权重，并举例说明了该问题。为了解决此问题，Wang Yingming等[21]又在前人基础上提出了一种全新的DEAHP方法，同时该方法不需要对比较矩阵进行标准化。因此，本文拟运用Wang Yingming等[21]提出的方法对保险、信贷和股票市场三个子系统内部各个指标的权重进行确定。具体模型如下：

给定一n×n阶互补比较矩阵A，该DEAHP模型具体为：

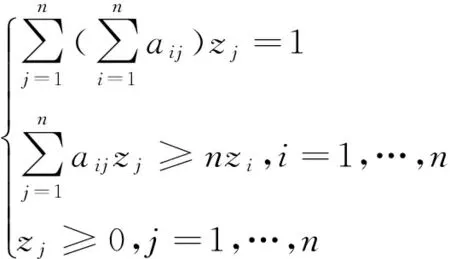
(5)

其中，aij为比较矩阵的元素；zj为待估计的指标权重。

3 动态协同演化模型的构建

考虑到保险、信贷与股票市场之间的相互影响过程中存在滞后性，而有关重要的社会事件、经济事件都将影响金融市场的运行过程，因此在构建保险、信贷与股票金融复合系统的动态协同演化模型时既要考虑各子系统间相互作用影响的滞后性，又要考虑相关重大社会事件、经济事件的影响。

3.1 模型的构建

设F1,F2,F3分别代表保险系统、信贷系统和股票系统，为了细致刻画这三个子系统演化进程中的相互竞争作用，引入参数βij(i,j=1,2,3)，即系统j对系统i的竞争影响参数。而针对于相关滞后项的确定，则采用广义向量自回归模型[22]。此时，保险、信贷与股票市场动态协同演化模型具体步骤分两步实现：

第一步，检验保险、信贷与股票市场三个子系统序参量的平稳性，依次确定其最大的单整阶数d和滞后阶数p，并将p+d期的滞后影响纳入到考虑范围。

第二步，构建保险、信贷与股票金融复合系统的动态协同演化模型，具体如下所示：

(6)

其中，θ1、θ2、θ3分别为重大社会事件、经济事件对三个子系统F1、F2和F3的影响；m表示发生重大社会事件、经济事件的年份。当t≤m时，则表示三个子系统没有受到重大社会事件、经济事件的持续影响，此时θ1=θ2=θ3=1；当t≥m+1时，三个子系统受到重大社会事件、经济事件的持续影响，此时θ1、θ2及θ3的大小需要估计得到。模型所模拟的实际情况为，重大社会事件、经济事件对某一个子系统的动态因子产生了直接影响，因此也不可避免地对三个子系统之间的相互作用关系产生了间接的影响。

进一步，因为保险、信贷与股票市场三个子系统的内部结构各不相同，因此不能仅运用上述三个参数对重大社会事件、经济事件对子系统的影响进行描述。因此，本人采用根据Balcilar等(2010)[23]的观点，将子系统j对子系统i的综合影响效果用式(7)表示：

(7)

3.2 模型稳定性分析

模型(6)给保险、信贷与股票市场三系统动态协同演化模型既考虑了重大经济事件对协同演化的影响，又考虑了相关影响具有滞后性的特点。其中，第一个演化方程刻画了信贷系统和股票系统对保险系统的影响效应是依靠参数β12r,β13r(r=0,1,…,p+d)表达的，无论是信贷市场的变化还是股票市场的变化均会对保险市场的有序度水平造成影响。而第二个演化方程则反映了保险系统和股票系统对信贷系统的影响是通过参数β21r,β23r(r=0,1,…,p+d)起作用的，保险市场和股票市场改善或者恶化都会为信贷业务发展起到促进或制约作用。第三个方程则呈现了保险系统和信贷系统对股票系统的作用是通过影响参数β31r,β32r(r=0,1,…,p+d)起作用的，因而无论是保险市场的变化还是信贷市场的变化也均会对股票市场的有序状态造成影响。

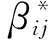
3.2.1 演化方程的稳定点

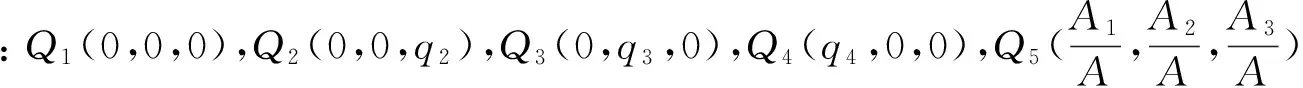
根据克莱姆法则，Q5点的坐标为：

(8)

微分方程平衡点Q5(X10,X20,X30)是否稳定的判别准则为：

(9)

(10)

(11)

其中，

当p<0,q<0,r<0时，平衡点Q5(X10,X20,X30)稳定；当p≥0时，平衡点Q5(X10,X20,X30)不稳定。

按照以上方法，可以计算出其他四个平衡点，计算公式如表1所示。

3.2.2 稳定点分析

系统的发展状态将随着时间的变化而变化，最终趋于稳定状态，而稳定点则代表系统的发展方向。首先，我们判断Q1(0,0,0)是不稳定点，因为在该点三个子系统都是完全无序状态，不可能发生稳定状态。Q2(0,0,q2)，Q3(0,q3,0)，Q4(q4,0,0)三个点分别为保险、信贷和股票市场的极值点，在极值点状态下三个子系统为了达到自身的最大值须以损害其他两个子系统为代价，任何一个子系统达到最优状态时另外两个子系统将处于灭亡状态。因此，Q2(0,0,q2)，Q3(0,q3,0)，Q4(q4,0,0)这三个点均为保险、信贷与股票金融复合系统的完全独立状态。平衡点Q5(X10,X20,X30)则对应三个子系统都在进行协同演化的状态。对此平衡点进行深入分析，能够发现出协同进化状态的两种情形：

第一种是部分竞争合作共存状态。这种状态相对应的稳定点是Q5(X10,X20,X30)，三个子系统之间的相互作用、相互影响程度不是均等的。在这种状态下，保险、信贷与股票金融三个子系统之间既存在着相互竞争的关系，又存在着相互合作的关系。当满足某种特定条件时，复合系统将达到最优状态，即三者可以实现协同进化，直到达到最优状态Q5。

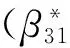
3.3 基于DNLPSO的模型参数求解

当前研究中一般采用极大似然估计法和最小二乘法对模型的参数进行求解。而本文所构建的保险、信贷与股票金融复合系统协同演化模型属于非线性模型，上述两种常规方法在对此类模型的参数进行求解时精度往往较低。鉴于此，本文拟借鉴前人的研究经验，运用改进型粒子群算法对模型参数进行求解[24]。这种基于局部性搜索和动态邻居的改进型粒子群算法不仅可以规避传统粒子群算法常常陷入局部最优解的不足，还具有计算总量较小、精度较高的优点。

表1 判别平衡点稳定性的计算公式

4 实证研究与分析

4.1 保险、信贷与股票市场复合系统的有序度分析

根据系统协调性院长，考虑数据的可获得性及我国实际情况，选取指标共20项。其中，保险系统指标分别为机构个数(家)、人员数(人)、原始保费收入(亿元)、原始人身保费收入(亿元)、原始人身保费占比(%)及赔付率(%)等6个指标；信贷系统指标分别为机构个数(家)、人员数(人)、存款总额(亿元)、人民币存款占比(%)、个人储蓄存款占比(%)、贷款总额(%)、人民币贷款占比(%)、短期贷款占比(%)等8个指标；股票系统指标分别为上市公司个数(家)、股票总股本(万股)、股票首发数量(万股)、股票筹资额(亿元)、股票开户数(万户)及股票交易(亿元)等6个指标。本文选取了2004-2013年间北京、天津、内蒙古、湖北、湖南、广东、辽宁、甘肃、宁夏、吉林、黑龙江、上海、江苏、浙江、重庆、四川、贵州、安徽、福建、江西、山东、广西、河北、山西、海南、云南、陕西、青海、新疆等30个省、自治区及直辖市作为样本，共300个观测值。由于西藏自治区和台湾地区的数据资料缺失过多，故被排除在外。各指标数据均来源于各省区历年《统计年鉴》。

结合选择好的指标体系和DEAHP方法，根据有序度计算公式(2)、(3)和(4)可以得到各省区2004-2013年间保险市场、信贷市场和股票市场的子系统有序度。进一步，利用简单加权平均法得到全国保险、信贷与股票系统的有序度水平，具体见图1。

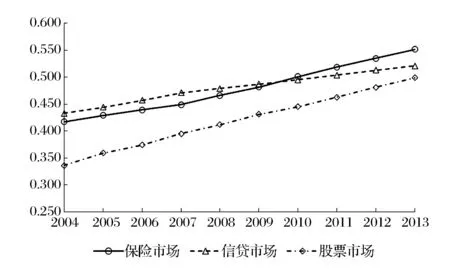
图1 全国保险、信贷与股票有序度变动趋势

由图1可以得到如下信息：(1)在2004-2013年间，保险、信贷与股票三个子系统的有序度均处于低下水平，这表明虽然我国保险、信贷与股票市场远离馄饨状态，但还存在很大的提升空间以实现完全有序状态。(2)2004-2013年间三者都呈现上升趋势，这说明我国保险、信贷与股票市场近年来都得到了长足发展。(3)从曲线的斜率变化来看，2008年之后保险系统的有序度上升趋势强劲，上升速度明显高于2008年之前，这说明金融危机对我国保险系统的发展有明显的推动作用。同时，2008年之后信贷和股票系统的有序度上升缓慢化，上升速度明显低于2008年之前，这说明2008年金融危机对我国信贷和股票系统的发展造成了一定的冲击。(4)在我国，股票市场的有序度水平最低，2010年之前信贷市场有序度略高于保险市场，随后被赶超，且呈现差异扩大化趋势。

4.2 保险、信贷与股票市场复合系统竞争合作关系分析

在2004—2013年间影响我国金融市场的事件有发生在2008年的全球性金融危机，因此有必要此次金融危机对我国保险、信贷与股票市场复合系统的协同进化产生的影响。因此，令m=2008。首先对有序度进行单位根检验，在此采用LLC、B-t、IPS、ADF及PP五种方法。考虑到有序度存在时间趋势，在此同时允许存在截距项和趋势项。结果显示，保险、信贷与股票系统的有序度均是一阶单整的，即d=1。进一步，利用LR、AIC、SC、HQ及FPE五种判别准则对传统VAR模型的滞后阶数进行确定，结果表明p=1。此时，p+d=2，即需要考虑三系统之间的2阶滞后影响。

进一步对得到的序参量指标进行一阶差分，此时DNLPSO模型目标函数为

表2 模型参数估计结果

(12)

(13)

(14)

利用前文提到的改进型粒子群算法求解模型参数，具体结果见表2。

不难发现，α1>α2>α3>0，这说明保险系统、信贷系统和股票系统都处于进化状态，且保险系统的进化速度最快，依次是信贷系统和股票系统。这说明近年来我国在保险、信贷和股票市场均取处于增长状态，尤其是近年来由于各方面因素导致通货膨胀压力逐步增加，政府则运用积极的财政政策来对宏观经济进行调控，通过深度拓展保险市场，优化资本市场投资环境，使得信贷市场和股票市场更加有序化。同时，由θ1>1>θ3>θ2>0可知，2008年的全球金融危机确实对保险、信贷与股票系统的协同演化进程产生了一定影响。金融危机时期金融投资环境质量下降也给保险市场的发展提供了空间，金融危机对保险系统的进化有显著的促进作用；相反地，正是由于投资环境的恶化导致信贷系统和股票系统发展进化受到一定的抑制，但未改变两者进化的状态。进一步，根据系统之间滞后项的参数可知，保险系统、信贷系统与股票系统之间的滞后影响确实对彼此的发展有重要影响。同时随着时间的推移，三者之间的竞争合作关系也发生了显著改变。

进一步，利用公式(7)得到保险系统、信贷系统与股票系统之间的累计相互作用关系，具体结果见表3。

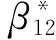
表3 三者之间的竞争合作关系

利用表2和表3中的参数分别对Q1、Q2、Q3、Q4、Q55个平衡点的稳定性判别值进行求解，结果如表4所示。

表4 平衡点稳定性判别值表

对上述5个平衡点所对应的稳定性判别值进行分析，可以得到以下结论：即只有Q5满足p<0、q<0、r<0时，它属于稳定点，其稳定点坐标是Q5(0.818,0.811,1.138)，表示保险、信贷与股票系统有序度在目前条件下的极值。随着复合系统的不断发展，保险系统、信贷系统与股票系统将处于一种协同进化状态。现实生活中，系统内部的协同演化不仅推动着复合系统整体朝着稳定点Q5不断发展，也推动着我国保险、信贷与股票系统三者各自的变化与发展，由此推动保险、信贷与股票金融复合系统朝着更高水准的稳定点不断地协同演化。

5 结语

作为金融市场的重要组成部分，保险、信贷与股票市场之间相互作用，构成一个复合系统。考虑到金融市场之间的滞后影响和重大经济事件影响是其重要特征，基于协同进化理论，本文建立了由保险、信贷和股票市场三者组成的复合系统协同动态演化模型，并对模型的稳定性进行了分析，同时给出了平衡点稳定性判别值表。随后，结合DNLPSO算法给出了模型参数求解方法。最后，利用2004-2013年间省际面板数据，对当前我国保险系统、信贷系统和股票系统的协同演化现状进行了实证研究。主要结论有：

(1)根据各省区有序度测算结果可知，2004-2013年间各省区保险、信贷与股票系统的有序度都呈现上升趋势，这说明我国保险、信贷与股票市场近年来得到了长足发展。然而，我国保险、信贷与股票系统有序度仍旧处于低下水平，这表明虽然我国保险、信贷与股票市场远离混沌状态，但还存在很大的提升空间以实现完全有序状态。此外，2008年金融危机后保险市场有序状态提升加速，而股票和信贷市场有序状态提升减速。

(2)由模型参数估计结果可知，当前我国保险、信贷与股票系统均处于进化状态，子系统的滞后项和2008年金融危机对复合系统的协同演化进程造成了重要的影响。其中，金融危机促进了我国保险系统的发展，在一定程度上抑制了信贷系统和股票系统的发展，但没有改变两者的演化方向。进一步，保险、信贷与股票系统之间同时存在竞争与合作，且滞后影响随着时间的推移发生了显著变化。三系统的累积作用显示，当前我国保险系统与信贷系统处于双输关系，信贷系统与股票系统同样处于双输关系，而保险系统和股票系统处于输赢互补关系。

(3)随着复合系统的不断发展，保险系统、信贷系统与股票系统将处于一种协同进化状态，三者之间的竞争演化、合作发展将推动我国保险、信贷与股票系统的协同演化进程，并向着稳定点演化。

本文提出的模型为金融系统的动态协同演化分析提供了一个研究范式，同时该模型也可以推广到其它复合系统的协同演化研究，比如社会、经济与资源环境组成的生态经济系统。由于该模型建立在Logistic增长方程的基础上，因而不适用于演化轨迹不符合S曲线的情形。同时，以外生冲击的形式将重要经济事件引入本文模型，如果复合系统内部发生结构性变化，则难以无法刻画。总之，三系统协同演化研究在国内尚处于起步阶段，因此如何结合复合系统自身特征构建更加接近现实的模型有待于进一步的深入研究。

[1] Mauro P. Stock markets and growth: A brief caveat on precautionary savings [J]. Economics letters.1995,47(1): 111-116.

[2] Webb I, Grace M F, Skipper H D. The effect of banking and insurance on the growth of capital and output [R]. Working Paper, Center of Risk Management and Insurance, 2002.

[3] Arena M. Does insurance market activity promote economic growth? A cross-country study for industrialized and developing countries [J]. Journal of Risk and Insurance, 2008,75(4): 921-946.

[4] 吴洪,赵桂芹.保险发展、金融协同和经济增长—基于省际面板数据的研究[J].经济科学, 2010,(3): 61-72.

[5] Macintosh R, Maclean D. Conditioned emergence: A dissipative structures approach to transformation [J]. Strategic Management Journal, 1999, 20(4): 297-316.

[6] Liu Ziming. Dissipative structure theory, synergetics, and their implications for the management of information systems [J]. Journal of the American Society for Information Science, 1996, 47(2): 129-135.

[7] 李朝霞.企业进化机制研究[M].北京：北京图书馆出版社，2001.

[8] 张华.协同创新、知识溢出的演化博弈机制研究[J].中国管理科学, 2016, 24(2): 93-99.

[9] 马宁,严太华,姬新龙.风险资本与智力资本协同条件分析与效应检验[J].中国管理科学, 2015, 23(3): 25-31.

[10] 张铁男,韩兵,张亚娟.基于B-Z反应的企业系统协同演化模型[J].管理科学学报, 2011, 14(2): 42-52.

[11] 马向东,孙金华,胡震云.正态环境与社会经济复合系统的协同进化[J].水科学进展, 2009，20(4): 566-571.

[12] Yang J M, Kim T W, Han H O. Understanding the economic development of Korea from a co-evolutionary perspective [J]. Journal of Asian Economics, 2006,17(4): 601-621.

[13] 吴价宝,卢珂.基于多主体的港口物流协同机制研究[J]. 中国管理科学，2014, 22(S1): 440-446.

[14] 玉胜贤,易华.三区联动理论研究述评[J]. 湖南商学院学报，2015, 22(1): 69-73.

[15] 范斐,孙才志,王雪妮.社会、经济与资源环境复合系统协同进化模型的构建及应用—以大连市为例[J].系统工程理论与实践, 2013, 33(2): 413-419.

[16] 崔强,匡海波,李烨.基于协同论和演化的交通运输方式低碳协同研究[J].中国管理科学，2014,22(S1): 852-858.

[17] 熊曙初,王敬童,罗毅辉.面向跨组织的电子政务协同服务机制研究[J].湖南商学院学报，2014,21(01)：108-112.

[18] Ramanathan R. Data envelopment analysis for weight derivation and aggregation in the analytic hierarchy process [J]. Computers and Operations Research, 2006(33): 1289-1307.

[19] 范斐,孙才志.辽宁省海洋经济与陆域经济协同发展研究 [J].地域研究与开发，2011,30(2)：60-63.

[20] Wang Yingming, Parkan C, Luo Ying. A linear programming method for generating the most favorable weights from a pairwise comparison matrix [J]. Computers and Operations Research, 2007,35(12): 3918-3930.

[21] Wang Yingming, Chin K S. A new data envelopment analysis method for priority determination and group decision making in the analytic hierarchy processes [J]. European Journal of Operational Research, 2009,195(1): 239-250.

[22] Toda H Y, Yamamoto T. Statistical inference in vector autoregression with possibly integrated processes [J]. Journal of Econometrics, 1995,66(1-2): 225-250.

[23] Balcilar M, Ozdemir Z A, Arslanturk Y. Economic growth and energy consumption causal nexus views through a bootstrap rolling window [J]. Energy Economics, 2010,32(6): 1398-1410.

[24] 刘衍民,隋常玲,赵庆祯.改进的粒子群算法求解Van Genuchten方程参数[J].系统工程理论与实践, 2011, 31(3): 512-521.

Co-evolutionary Analysis on the Composite System of Insurance,Credit and Stock Markets

REN Teng1, ZHOU Zhong-bao2

(1.School of Logistics and Transportation, Central South University of Forestry and Technology, Changsha 410018，China;2. School of Business Administration, Hunan University, Changsha 410082, China)

The co-evolution analysis is critical for managers to understand the internal mechanism of composite system, without exception to financial system with insurance, banking and stock markets. There are only few researches on the issue of the composite system with two subsystems using time series, and how to assess the dynamic relationship of the composite system with three or more subsystems is underestimated. Especially, the lag effect across different subsystems is very common in the real world, and some economic and management policy as well as major events have remarkable effects on the operation of composite system. Furthermore, considering the fact that the sample in time series is always ineffective to estimate the coefficients in the co-evolutionary equation, it is necessary to propose a new method which can be applied to panel fata. To overcome the three drawbacks, in this paper, a general framework is built.

Based on the theoretical analysis of the linkages among insurance， credit and stock markets, combining synergistic theory and the improved PSO based on dynamic neighbor topology and local search (DNLPSO), a dynamic co-evolution model is proposed for analyzing the development process of three opening multiplexed system. The computation method for order degree is constructed on the basis of DEAHP, and then the corresponding computational approach is given based on DNLPSO algorithm. Further, the stability analysis of the new co-evolutionary model is given. With the nonlinear relationship among differentsubsystems taken into consideration, the parameters of structural change and lag structures depict the impact of major events and lag effects. Using provincial penal data, the empirical study of coordination evolves in insurance, credit and stock composite systems covering 2004-2013 is unfolded. Results indicate that this model reflects the effects of lag structures and the 2008 financial crisis well, and manifests this complicated system’s partial relevance and the whole evolution trends stable completely, and puts forward a basic paradigm for empirical analysis on co-evolution of three composite systems.

dynamic co-evolution；stability analysis；DNLPSO algorithm；composite system

1003-207(2017)08-0079-10

10.16381/j.cnki.issn1003-207x.2017.08.009

2016-02-21；

2017-02-15

国家自然科学基金资助项目(71371067)；教育部人文社科基金项目(16YJC630101)；湖南省社科基金项目(15YBA407)；湖南省教育厅优秀青年基金项目(14B188)

任腾(1988-)，男(汉族)，湖南常德人，中南林业科技大学物流与交通学院讲师，管理学博士，研究方向：金融工程与风险管理、系统优化与决策,E-mail:chinarenteng@163.com.

F830

A