高维条件协方差矩阵的非线性压缩估计及其在构建最优投资组合中的应用

赵 钊

(华中科技大学经济学院，湖北 武汉 430074)

高维条件协方差矩阵的非线性压缩估计及其在构建最优投资组合中的应用

赵 钊

(华中科技大学经济学院，湖北 武汉 430074)

本文将非线性压缩方法运用到DCC和BEKK模型中，用非线性的压缩估计量代替MMLE估计中初始的样本协方差矩阵，大大提高了高维DCC和BEKK模型的估计效率，并突破性地使得横截面维度大于时间维度时，DCC和BEKK模型的有效估计成为可能。蒙特卡洛模拟发现：非线性压缩方法对于DCC和BEKK模型估计的优化作用显著，且优化程度随着横截面维度和时间维度的比值增大而增加。实证分析进一步说明了非线性压缩方法对于准确估计高维条件协方差矩阵、从而提高组合选择效率的重要作用。

非线性压缩；线性压缩；条件协方差矩阵

1 引言

随着信息技术的发展，高维数据越来越频繁地出现在各个领域，且表现出横截面维度和时间维度均趋于无穷、或横截面维度超过时间维度的特征，这时，传统的统计推断理论因面临着维数诅咒、噪声影响等诸多挑战而不再适用。例如，在构建资产组合或风险管理时，准确估计各资产之间的协方差矩阵对于配置最优资产权重十分重要。当横截面维度相对于样本长度较小时，样本协方差矩阵是未知总体协方差矩阵的有效替代；但对于共同基金经理，更常见的情况是，横截面维度超过或者接近时间维度，这时，样本协方差矩阵将是奇异矩阵或近奇异矩阵，从而不存在逆矩阵，或者即使存在，也是真实总体协方差逆矩阵的有偏估计量。

用来解决这一难题的方法，按照是否对协方差矩阵的结构进行外生假定，可以分为两大类。其中添加了结构假定的方法主要包括矩阵稀疏法和因子模型，前者直接假定协方差矩阵为稀疏矩阵，即其中绝大多数元素都为零或接近零(如Lam和Fan Jianqing[1]，Rigollet和Tsybakov[2])，后者假定除去共同因子后剩余成分的协方差矩阵为稀疏矩阵，这种假定与实际金融市场的特征更符合，因此，因子模型的运用更为广泛。因子模型，按照因子是否可观测又分为可观测因子模型和潜因子模型。最典型的可观测因子模型有：以价值加权的市场回报为可观测单一因子的CAPM模型，以代表企业性质的多变量为可观测因子的Fama和French[3]三因素模型，Chen等[4]提出的以通胀率、利率等宏观变量为可观测因子的多因素模型。与此相对，潜因子模型假定因子是未知的，最典型的例子如Ross[5]提出的无套利定价理论，即假定资产回报存在因子结构，因而风险溢价可以表述为因子载荷的线性函数。

另一类高维协方差矩阵估计的方法不对协方差矩阵的结构进行任何先验的假定，而是依靠偏误的修正来对样本协方差矩阵进行改进。我们知道，当横截面维度较大时，样本协方差矩阵较大的偏误主要来源于相关系数的偏误，即正(负)的偏误来源于过高(低)的系数估计。压缩估计方法的基本思想就是将相关系数中这种正(负)的偏误向下(上)拉回。其中，线性压缩估计量即为样本协方差矩阵和一个条件良好的结构化估计量的加权平均，其中权重是根据给定的二次损失函数确定的最优值，而结构化估计量则可有多种选择，如样本均值单位阵(Ledoit和Wolf[6])，单指数模型得到的协方差矩阵(Ledoit和Wolf[7])，等相关系数矩阵(Ledoit和Wolf[8])等。非线性压缩估计则是在一组与样本协方差矩阵“旋转等变”的估计量中选择出与总体协方差矩阵最接近的最优解。但由于代数求解出的最优解依赖于未知总体协方差矩阵，因此是不可得的，Ledoit和Wolf[9-11]通过系列文章研究如何利用随机矩阵理论，将这种不可得的最优解转换为仅依赖于样本特征值极限分布的理想(Oracle)估计量，最后进一步转换成渐近性质良好的可实现(Bona fide)估计量。

上述方法都是针对无条件的高维协方差矩阵估计，但普遍认为，在金融研究中，前期信息对协方差矩阵有着重要影响，因此，相比之下，条件协方差矩阵更为适用。在研究金融资产回报协方差随时间变化的模型中，多变量广义自回归条件异方差(GARCH)模型被运用得最为广泛，主要包括Bollerslev等[12]的VEC模型，Engle和Kroner[13]的BEKK模型，Engle[14]的DCC模型，Ledoit等[15]的放松条件的多变量GARCH模型，Cappiello等[16]的不对称DCC，Engle和Kelly[17]的动态等相关系数模型。虽然GARCH模型已被广泛接受和使用，但当横截面维度较大时，其估计效果并不理想，主要原因是其中涉及到的初始无条件样本协方差矩阵的估计因受冗余维度的影响而存在较大偏误。因此，如果能将高维无条件的协方差矩阵估计方法运用到GARCH模型初始样本协方差矩阵的估计中，理论上将能很好地改善高维GARCH模型的表现。

刘志东和薛莉[18]提出具有“杠杆效应”的广义正交GARCH模型，并采用不同的统计技术实现基于交互信息最小化的参数估计方法。刘丽萍等[19]提出将主成分和门限方法结合并运用到DCC模型的估计中，并通过蒙特卡洛模拟和实证研究说明这一方法明显提高了高维条件协方差矩阵估计的效率。张贵生和张信东[20]提出基于近邻互信息特征选择的SVM-GARCH模型，并通过仿真实验说明了SVM处理高维非线性数据的优势使得这一模型优于传统的ARMA-GARCH模型。Hafner和Reznikova[21]提出将线性压缩方法运用到DCC的估计中，同样通过蒙特卡洛模拟和实证研究说明了这一处理方法能有效地改善高维条件协方差矩阵的估计结果。注意到，这些研究中，横截面维度的最大值都被限制在200以内，且时间维度仍远大于横截面维度，并未真正突破传统统计推断理论的条件限制。本文借助于非线性压缩方法，通过将其运用到DCC和BEKK的估计中，使横截面维度大于时间维度时，条件协方差矩阵的有效估计成为可能，并通过蒙特卡洛模拟说明了非线性压缩方法对估计DCC和BEKK模型的有效优化，且这种优化作用随着横截面维度和时间维度比值的增大而增强。最后，本文通过构建美国股市的最小方差组合，进一步说明了非线性压缩估计GARCH模型对提高组合选择效率、降低组合风险的重要作用。

2 模型

2.1 模型的设定

设{xt}是一个N×1的随机过程向量，θ为参数向量，μt(θ)为其条件均值向量，Ht(θ)为其条件协方差矩阵，则xt可以写成如下形式：

xt=μt(θ)+εt

(1)

(2)

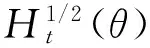
BEKK模型假定：

(3)

其中C，Ak，Bk都是N×N的矩阵。当K=1时，模型就有N(5N+1)/2个待估参数。为了减少高维情况下待估参数的个数，一般假定Ak和Bk为对角矩阵(对角BEKK)，或更进一步，假定Ak和Bk为标量(标量BEKK)。例如，K=1的标量BEKK模型为：

Ht=C+αεt-1εt-1′+βHt-1

(4)

DCC模型的基本思想是将随机变量的波动和变量间的相关系数分离。假定：

Ht=DtRtDt

(5)

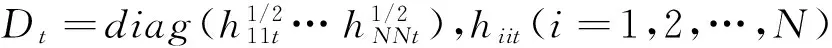
(6)

对于相关系数矩阵，Engle[14]假定:

(7)

其中正定矩阵Qt=(qijt)满足:

(8)

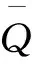
2.2 模型的估计

假定模型的新息zt服从独立的标准正态分布，利用一般的拟最大似然估计法(QMLE)，我们只需最大化如下的样本拟似然函数：

(9)

特别地，对于DCC模型，我们将待估参数分为波动参数ψ和相关系数参数φ=(α,β)两组，这样，波动矩阵Dt可记为Dt(ψ)，相关系数矩阵Rt则可记为Rt(ψ,φ)。模型的样本似然函数被分为两个部分，然后相继进行最大化估计：

L(θ)=Lv(ψ)+Lc(ψ,φ)

(10)

其中

(11)

(12)

首先，最大化波动参数的拟似然函数，得到波动参数ψ的估计量:

(13)

(14)

正如Engle等[22]所述，在高维模型中，最大化样本拟似然函数面临两个难题。第一个难题是，当横截面维度大时，待估参数过多，即使是最简化的标量BEKK(1,1)模型也存在N(N+1)/2+2个待估参数。解决这一问题的方法是把一些冗余的待估参数分离出来，用基于矩的估计量代替其基于拟最大似然法的最优解，从而避免其对整体拟似然函数形成负荷。Engle和Mezrich[23]提出在标量BEKK模型中，以“协方差为目标”，从而得到截距C矩阵基于矩的估计量为：

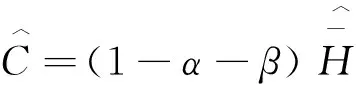
(15)

其中

(16)

(17)

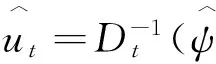
第二个难题是在计算样本拟似然函数时需要多次对N维矩阵Ht求逆。针对这一问题，Engle等[22]提出一种复合拟最大似然法(CL)代替普通的拟最大似然法来估计多变量GARCH模型，即通过加总资产子集的拟似然值，避免了对高维的协方差矩阵求逆，从而大大提高估计高维GARCH模型的效率。

具体而言，该方法首先由原始数据{xt构建数据子集Yjt=Sjxt，其中Sj是一个非随机的选择矩阵，如任意挑选N维时间序列数据集中的两组时间序列数据进行组合，Sj即为一个2×N的矩阵，这样可以形成M=N(N-1)/2个组合：Y1t=(x1t,x2t)′，…，YMt=(xN-1,t,xNt)′。容易得到，在信息集Ft-1已知的条件下，Yjt的条件期望和条件协方差分别为：

E(Yjt|Ft-1)=Sjμt(θ)

(18)

Cov(Yjt|Ft-1)=Hjt=SjHtSj′

(19)

由此，我们得到第j个组合t时期的有效拟似然函数：

(20)

对所有M个组合的拟似然函数值求平均，得到t时期的复合拟似然函数(CL)：

(21)

最后，按时间加总得到样本CL函数

(22)

即:

(23)

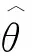
2.3 压缩方法及其在GARCH模型中的运用

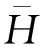
用压缩方法改善样本协方差矩阵的性质，最早是由Stein[24-25]提出的。该方法的基本思想是：首先，通过压缩样本协方差矩阵的特征值，而同时保留特征向量不变，来构建一组与样本协方差矩阵“旋转等变”的估计量；然后，最小化规模不变的损失函数选出最优的估计量。压缩方法的本质是将较小的特征值放大，将较大的特征值缩小，从而使样本特征值的范围向均值压缩。

设X为xit构成的T×N维观测值矩阵，当T→∞时，N/T→c。总体协方差矩阵ΣT为N维非随机正定矩阵，λi为其第i个最大的特征值，ξi为对应的特征向量；bi是N维样本协方差矩阵ST第i个最大的特征值，ui是对应的特征向量。与ST“旋转等变”的估计量集为：

(24)

其中矩阵UT的第i列为样本特征向量ui，DT=Diag(d1,…,dN)。我们的目的是在这一系列估计量中找到与总体协方差矩阵ΣT最为接近的那个。如果用Frobenius范数来测度估计量矩阵与总体协方差矩阵之间的距离，则我们的最优化问题变为：

(25)

容易求得最优解为:

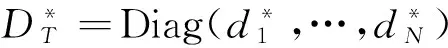
(26)

从而得到最优的协方差矩阵估计量为:

(27)

Ledoit和Wolf[6-8]提出了三种线性压缩目标矩阵对样本协方差矩阵进行压缩，分别为：由单指数模型得到的协方差矩阵，样本均值单位阵和等相关系数矩阵，其中样本均值单位阵被认为是最简单有效的目标压缩阵。Hafner和Reznikova[21]的模拟和实证结果也说明样本均值单位阵的表现优于其它两种压缩目标。基于此，我们选择样本均值单位阵作为线性压缩目标阵以及非线性压缩最优化问题求解的初始值。于是，得到特征值的线性压缩函数为：

(28)

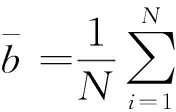
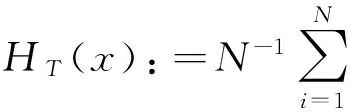
设Re(z)和lm(z)分别表示复数z的实部和虚部；表示复数集，+表示有严格正虚部的复数集；对于任意实数域上的非降函数G，sG表示其Stieltjes转换：

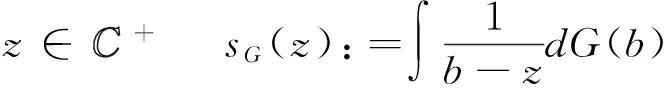
(29)

当函数G在a和b处连续时，Stieltjes转换满足如下的公式：

(30)

且s:=sF(z)是集合{s∈中，以下方程的唯一解：

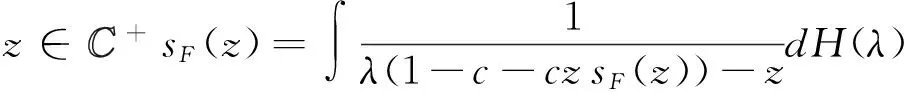
(31)

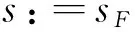
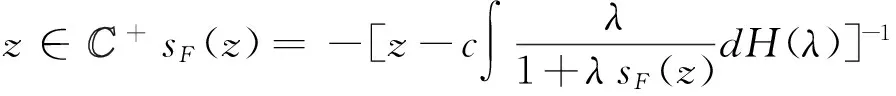
(32)

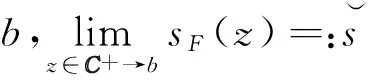
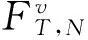
QT,N:[0,∞)N→[0,∞)N

(33)

v:=(v1,…,vN)′

(34)

其中，

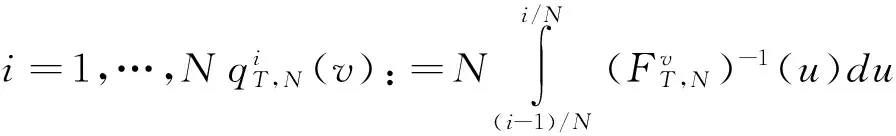
(35)

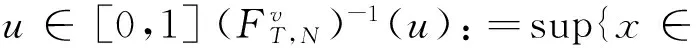
(36)

∀x∈

(37)

(38)

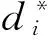
(39)

并进一步给出相对应的可实现(Bona fide)估计量：

(40)

其中，

(41)

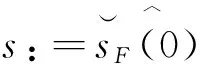
(42)

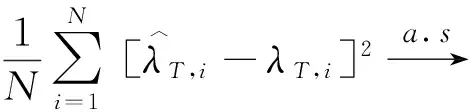
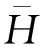
3 蒙特卡洛模拟

这一部分，我们将通过蒙特卡洛仿真模拟比较非线性压缩、线性压缩对DCC、BEKK模型，以及非线性压缩对线性压缩估计的改善。我们研究的方法包括： DCC估计，DCC单位阵线性压缩(DCCI)估计，DCC非线性压缩(DCCNL)估计，BEKK估计，BEKK单位阵线性压缩(BEKKI)估计，BEKK非线性压缩(BEKKNL)估计。Engle等[22]的模拟实验发现CL方法中，子集的选择方式对于结果的影响不显著。毗邻配对(M=N)相对于穷尽所有可能配对(M=N(N-1)/2)表现几乎同样好，却大大减少了计算量。因此，对所有这些模型，我们都采用毗邻配对的复合拟最大似然法(CL)进行估计。

为了使结果更有效，针对DCC和BEKK模型，我们分别设计了两组数据生成过程(DGP)。对于DCC模型，真实的DGP为：

(43)

(44)

(45)

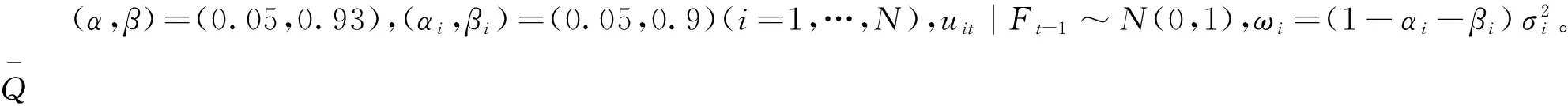
Ht=C+αεt-1εt-1′+βHt-1

(46)

同样设定(α,β)=(0.05,0.93)，C=(1-α-β)Σ，其中Σ是根据2005-2014年NASDAQ和NYSE所有上市股票日回报率数据估计的样本协方差矩阵。

对于两组实验，我们考虑同样的横截面维度和时间维度，分别为：N=30,50,100,250,500，T=100,250,500,1000，蒙特卡洛模拟重复次数都为S=100。我们将通过平均损失的相对改善(PRIAL)来比较组内各方法估计条件协方差矩阵的准确性，其定义为：

(47)

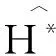
鉴于我们的最终目的是尽可能准确的估计条件协方差矩阵，从而构建最优资产组合，选择Ledoit和Wolf[10]用到的损失函数将最为适合：

(48)

由于DCC和BEKK两组实验设计的真实DGP不同，真实的总体协方差矩阵也不同，比较两组方法的损失函数或PRIAL都缺乏意义，因此，我们将通过两组实验估计参数的偏误(BIAS)和均方误差(RMSE)对两组方法进行总体上的比较，其定义如下：

(49)

(50)

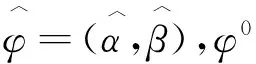
图1和图2分别为DCC组和BEKK组模拟的最终结果，其中点线和虚线分别表示非线性压缩和线性压缩相对标准模型的PRIAL，实线则表示非线性压缩相对线性压缩的PRIAL。可以得到如下结论：

(1)无论对于DCC模型还是BEKK模型，压缩估计量的表现一致优于标准模型。DCCNL和DCCI相对DCC的PRIAL、BEKKNL和BEKKI相对BEKK的PRIAL都恒大于零，且都随着横截面维度与时间维度的比值增大到1而趋于增加到100%。T=100时，随着横截面维度N从30增加到100，DCCNL和DCCI相对DCC、BEKKNL和BEKKI相对BEKK的PRIAL都从约30%增长到接近100%。T=250时，随着横截面维度N从30增加到250，相应的PRIAL都从约10%增长到接近100%。T=500时，随着横截面维度N从30增加到500，相应的PRIAL都从约5%增长到接近100%。

(2)对于DCC模型和BEKK模型，都表现出非线性压缩优于线性压缩估计的特征。首先，比较非线性压缩相对线性压缩的PRIAL，我们发现：DCCNL相对DCCI的PRIAL恒大于零，且当N≤T时，这一PRIAL值随着横截面维度的增加而增大，说明在大横截面维度下，非线性压缩相对线性压缩的优势更为明显。当N>T时，DCCNL相对DCCI的PRIAL虽然相对有所下降，但仍显著大于零。在BEKK模型中，虽然非线性压缩相对线性压缩的优势不如在DCC模型中明显，但整体上，仍可发现非线性压缩方法的优越性。除了T=100，N=100等少数组合，非线性压缩方法相对线性压缩的PRIAL在多数情况下都大于零，且随着横截面维度的增加而增大。其次，比较非线性压缩和线性压缩分别相对标准模型的PRIAL，我们发现：对于DCC组和BEKK组，点线都几乎总是高于虚线，这说明，非线性压缩相对标准模型的PRIAL几乎处处大于线性压缩相对标准模型的PRIAL，从而进一步说明非线性压缩相对线性压缩存在一致优势。

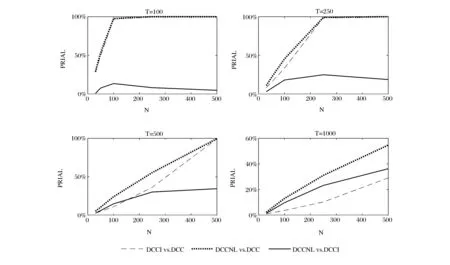
图1 DCCI、DCCNL相对DCC，DCCNL相对DCCI的平均损失改善(PRIAL) 注：横轴为横截面维度N，纵轴为平均损失的相对改善(PRIAL)

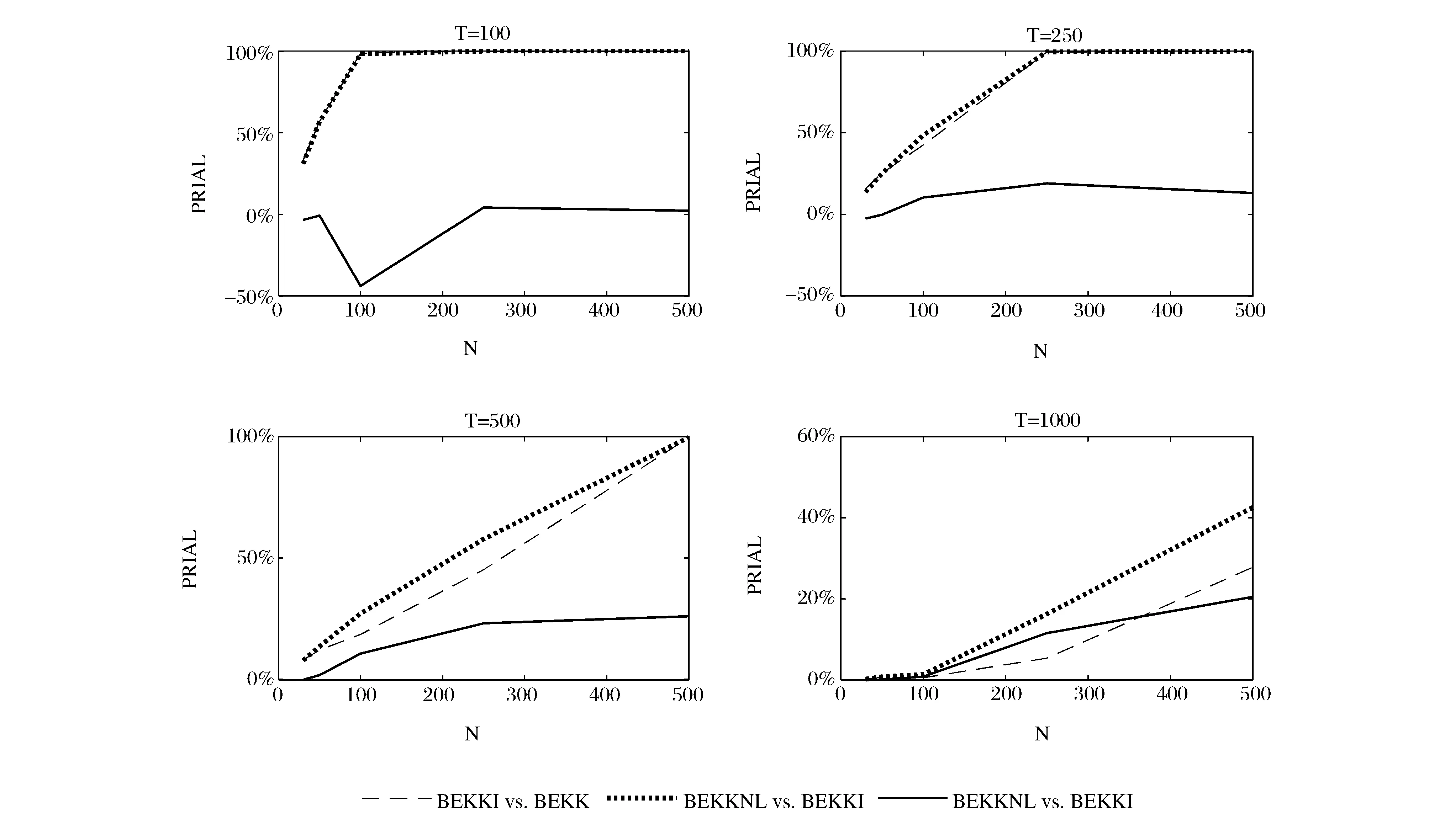
图2 BEKKI、BEKKNL相对BEKK，BEKKNL相对BEKKI的平均损失改善(PRIAL) 注：横轴为横截面维度N，纵轴为平均损失的相对改善(PRIAL)

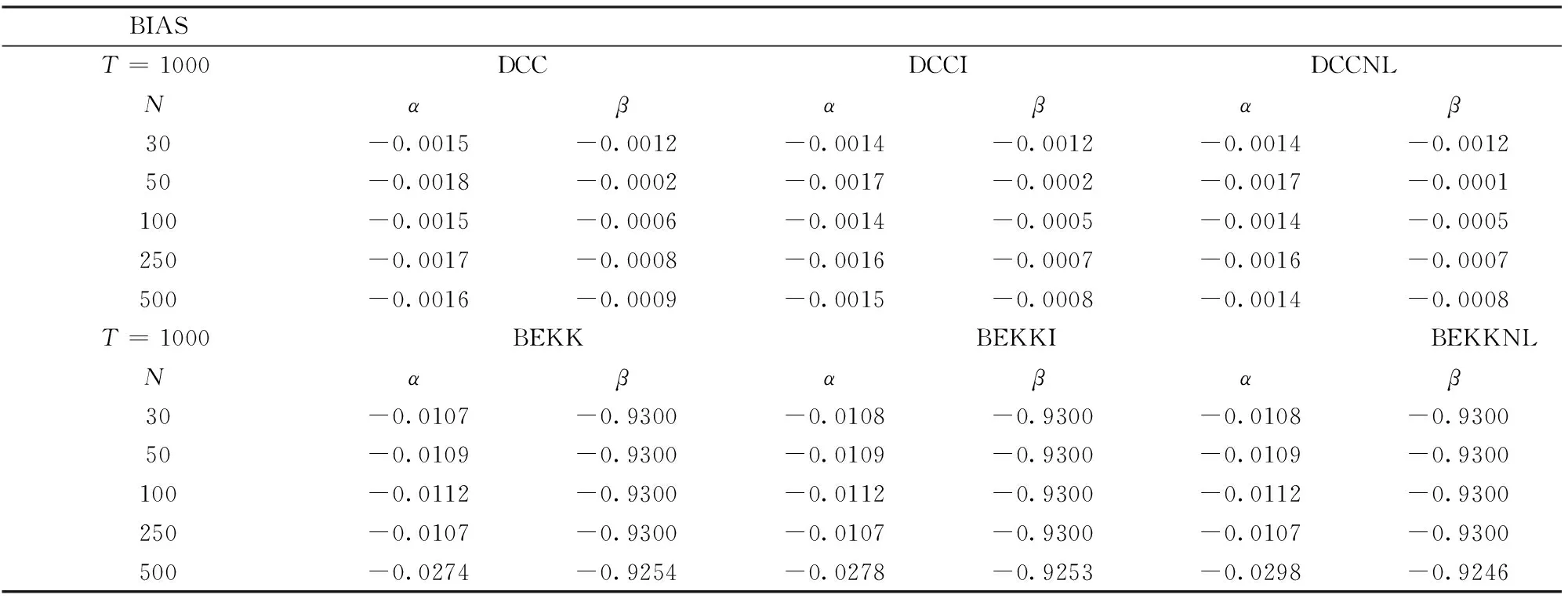
BIAST=1000DCCDCCIDCCNLNαβαβαβ30-0.0015-0.0012-0.0014-0.0012-0.0014-0.001250-0.0018-0.0002-0.0017-0.0002-0.0017-0.0001100-0.0015-0.0006-0.0014-0.0005-0.0014-0.0005250-0.0017-0.0008-0.0016-0.0007-0.0016-0.0007500-0.0016-0.0009-0.0015-0.0008-0.0014-0.0008T=1000BEKKBEKKIBEKKNLNαβαβαβ30-0.0107-0.9300-0.0108-0.9300-0.0108-0.930050-0.0109-0.9300-0.0109-0.9300-0.0109-0.9300100-0.0112-0.9300-0.0112-0.9300-0.0112-0.9300250-0.0107-0.9300-0.0107-0.9300-0.0107-0.9300500-0.0274-0.9254-0.0278-0.9253-0.0298-0.9246

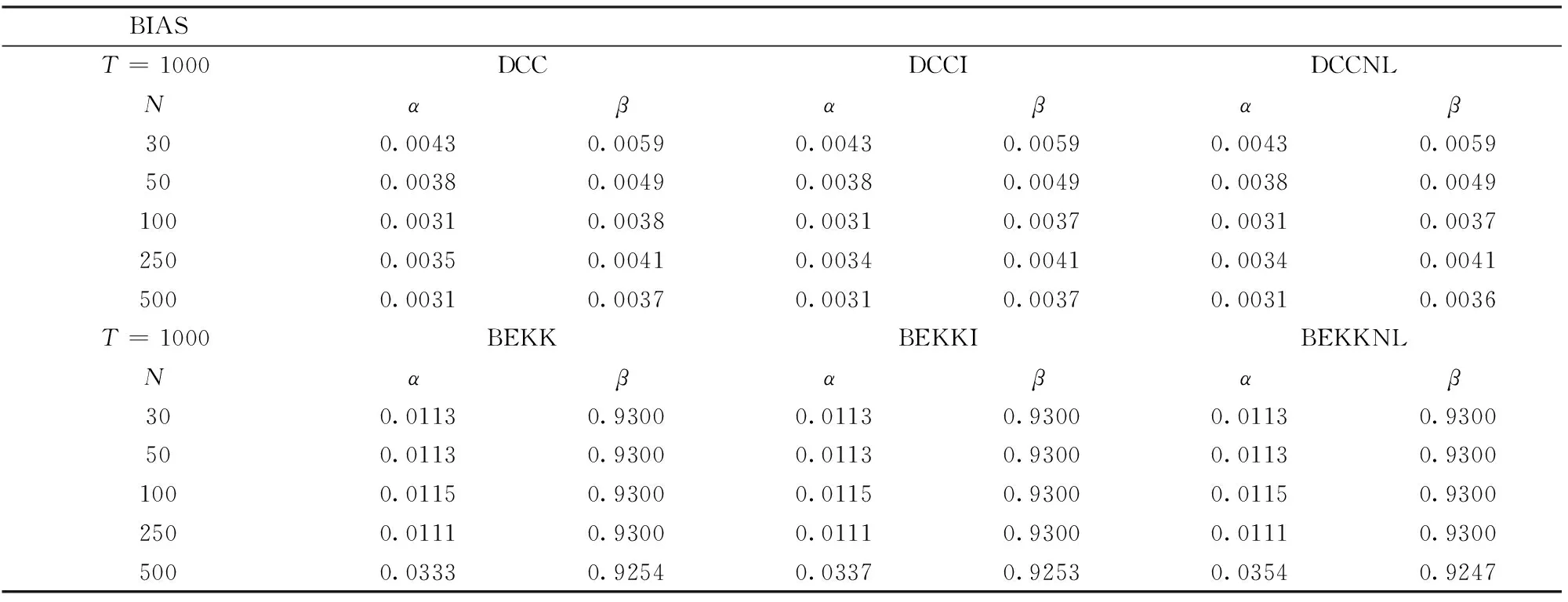
表2 DCC，DCCI，DCCNL，BEKK，BEKKI，BEKKNL六种估计方法的RMSE

(3)非线性压缩方法相对于标准模型和相对线性压缩估计的优势都在DCC模型中表现得更为显著。一方面，T=1000时，随着横截面维度N从30增加到500，DCCNL相对DCC的PRIAL从约2%增长到超过50%，而BEKKNL相对BEKK的PRIAL从接近0增长到略高于40%。另一方面，在DCC模型中，非线性压缩相对线性压缩的PRIAL一致高于同样横截面维度和时间维度条件下BEKK模型相应的PRIAL。

最后，为节省篇幅，我们在表1和表2中仅给出T=1000时，两组实验估计参数的BIAS和RMSE作为比较两组实验估计精度的参考指标。不难发现，两组实验对参数的估计都一致性地产生轻微的负偏误，但DCC组的BIAS和RMSE都大大低于BEKK组，这说明DCC对于参数α和β的估计更为准确。另一方面，我们发现，非线性和线性压缩方法都没有显著降低参数估计的BIAS和RMSE，这说明压缩方法没有修正参数估计偏误的作用，考虑到压缩方法仅作用于初始协方差矩阵的估计，这一结论与理论预期也是相符的。

4 实证分析

4.1 数据

本文的数据来源于证券价格研究中心(CRSP)，包含了1991年1月1日到2015年12月31日之间，NASDAQ和NYSE上市的市值最大的前1000支股票的日回报率。

为简化计算且不失一般性，我们假定：一个交易月由21个连续的交易日组成；每个交易月的月初，我们对构建的组合进行一次更新；每次更新是基于最近的前250个交易日的回报数据提供的信息，即T=250；样本外预测期间是1991年12月31日到2015年12月31日，一共包含了288个交易月(6048个交易日)，即进行了288次组合构建。

在每一个组合构建更新日，我们选择投资域的具体做法是：首先，选择出更新日最近的前250个交易日和后21个交易日都存在完整日回报率数据的股票，如假定更新期为h，则我们需要股票在h-250到h+20的时间区间内数据完整。第二，在每一个更新日，对满足上述条件的股票按市值大小进行排序，选择市值最大的前500支股票。第三，在这500支股票中，随机选择出N支股票。与仿真模拟部分一致，我们构建的组合大小(即横截面维度N)将包含如下集合：{30,50,100,250,500}。这一横截面维度集的选择涵盖了包括道琼斯工业平均、S&P 500等在内的大部分重要指数的横截面维度。

4.2 构建最小方差组合

我们构建无卖空约束的最小方差投资组合(GMV)，如下：

(51)

s.t.ω′1=1

(52)

其中ω为投资组合的权重向量，Σ为投资组合的协方差矩阵，1表示所有元素都为1的N×1维向量。这一最小化问题的解为：

(53)

我们将比较以下7种协方差矩阵估计方法：

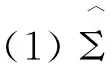
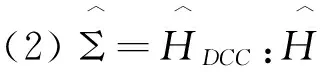
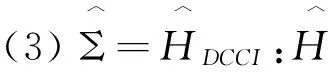
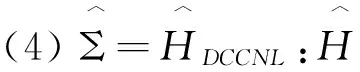
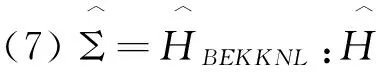
对于这7种方法构建的组合，我们都将计算年化的平均超额回报率(AR)、年化的标准差(SD)和年化的夏普尔率(SR)。由于我们构建的是最小方差组合，因此，年化的标准差(SD)是判断总体协方差估计表现的最重要指标，AR和SR则只是评价表现的辅助指标。由表3呈现的结果，我们可以得到如下结论：

(1)与理论预期一致，所有GMV组合的标准差都随着横截面维度N增加而减少，且不同方法所得标准差减少程度差异悬殊：随着N从30增长到500，单位矩阵方法的标准差仅减少了5%，而DCCNL和BEKKNL的标准差则分别减少了约34%和29%。

(2)当N=30,50,100时，所有的估计方法都始终显著优于单位矩阵；当N=250,500时，横截面维度N等于或超过时间维度T，DCC和BEKK方法得到的协方差矩阵都是近奇异矩阵或奇异矩阵，因此估计结果无效，这时，压缩方法的优势表现得尤为明显。

(3)DCCNL估计GMV的表现一致优于DCCI，而DCCI则一致优于DCC；同样，BEKKNL一致优于BEKKI，BEKKI一致优于BEKK。且这种优势都随着横截面维度N增加而增大。当N从30增大到100时，DCCNL对DCCI和DCC的标准差优化分别从不足1%增加到7%，和从约3%增加到13%；BEKKNL对BEKKI和BEKK的标准差优化则分别从不足0.1%增加到2%，以及从约1%增加到10%。

(4)DCC系列的3组组合整体上优于BEKK系列对应的3组组合。当N从30增大到100时，DCC对BEKK的标准差优化从2.5%增加到5%；当N从30增加到500，DCCI对BEKKI的标准差优化则从3%增加到10%，DCCNL对BEKKNL的标准差优化则从4%增加到11%。这意味着在所有7种组合构建方法中，DCCNL表现最优。

总之，在估计样本外协方差矩阵时，若时间维度一定，随着横截面维度逐渐增大，非线性压缩估计相对线性压缩及标准模型的优势都越来越明显，DCC系列相对BEKK系列的优势也越来越明显。

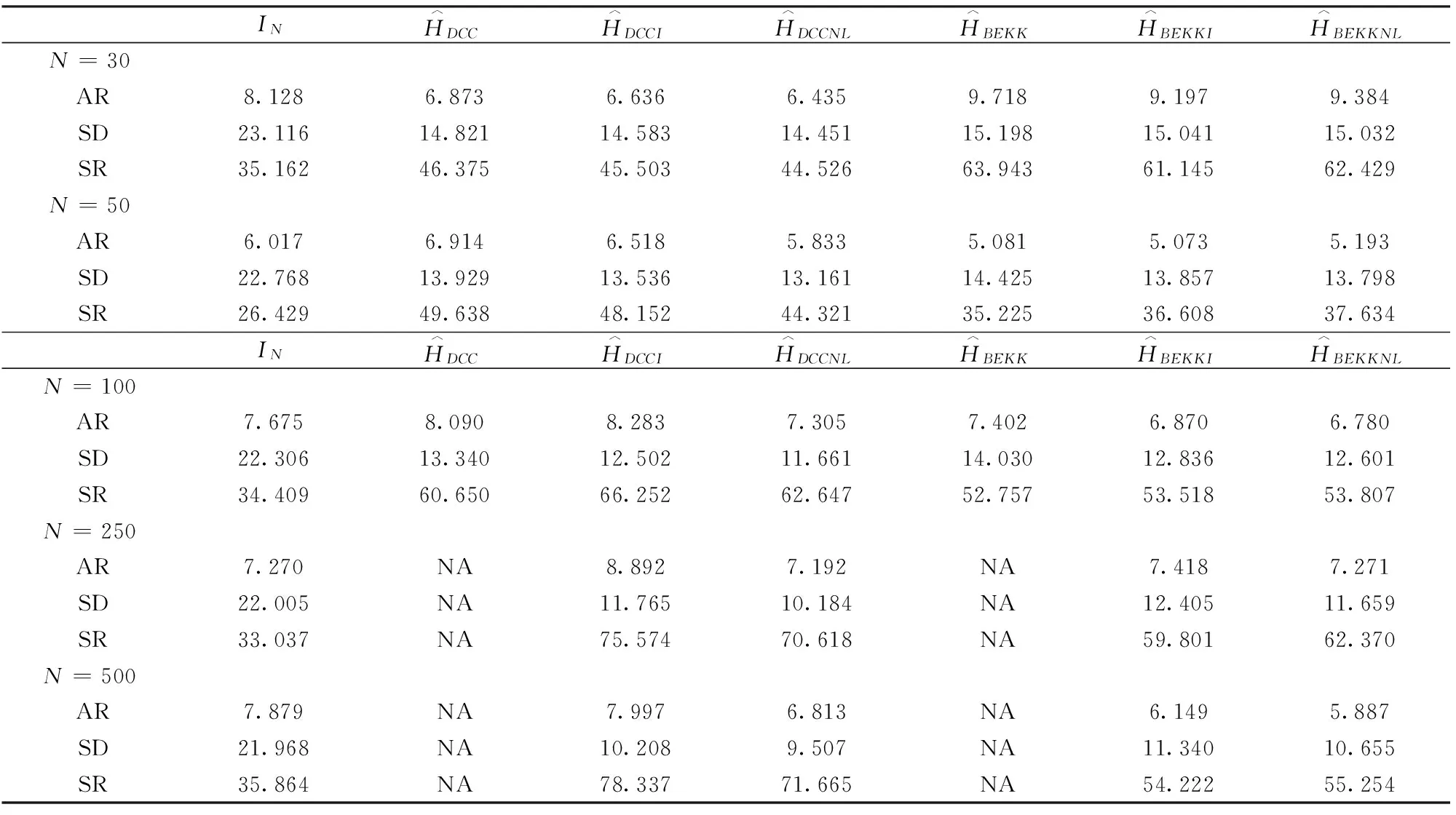
表3 不同方差估计GMV组合的年化AR、SD和SR

5 结语

本文将非线性压缩方法运用到DCC和BEKK模型基于矩的拟最大似然估计(MMLE)中，一方面继承了MMLE估计的优点，大大减少了高维情况下拟似然函数中待估参数的个数，另一方面有效解决了MMLE方法存在的初始协方差矩阵估计不一致的问题，大大提高了GARCH模型的估计效率，更重要的是，通过非线性压缩方法使得横截面维度大于时间维度时GARCH模型的有效估计成为可能，从而突破了GARCH模型对维度的限制，这对于估计高维条件协方差矩阵有着重要的理论意义。

本文方法的核心是用非线性压缩估计量代替MMLE方法中存在偏误的初始协方差矩阵估计量，其中非线性压缩方法沿用了Ledoit和Wolf[10]提出的非线性转换。通过蒙特卡洛模拟，我们发现，一方面，对于DCC和BEKK都有：非线性压缩一致优于线性压缩，线性压缩一致优于标准模型，且非线性压缩对于线性压缩和标准模型的优化程度都随着横截面维度和时间维度的比值增大而增加。另一方面，DCC表现优于BEKK，且非线性压缩方法对于模型效率的优化程度，DCC也高于BEKK。实证研究则进一步验证了这一结论，说明了非线性压缩方法与GARCH模型的结合对于高维资产组合的构建有着十分重要的现实意义。

[1] Lam C, Fan Jianqing.Sparsistency and rates of convergence in large covariance matrix estimation [J]. Annals of Statistics, 2009,37(6B):4254-4278.

[2] Rigollet P, Tsybakov A B. Sparse estimation by exponential weighting [J]. Statistical Science, 2012,27(4):558-575.

[3] Fama E F, French K R. Common risk factors in the returns on stocks and bonds [J]. Journal of Financial Economics, 1993,33(1):3-56.

[4] Chen N F, Roll R, Ross S A.Economic forces and the stock market [J]. Journal of Business, 1986,59(3):383-403.

[5] Ross S A.The arbitrage theory of capital asset pricing [J]. Journal of Economic Theory, 1976,13(3):341-360.

[6] Ledoit O, Wolf M. A well-conditioned estimator for large-dimensional covariance matrices [J]. Journal of Multivariate Analysis, 2004,88(2): 365-411.

[7] Ledoit O, Wolf M.Improved estimation of the covariance matrix of stock returns with an application to portfolio selection [J]. Journal of Empirical Finance, 2003,10(5):603-621.

[8] Ledoit O, Wolf M.Honey, I shrunk the sample covariance matrix [J]. Journal of Portfolio Management, 2004,30(4):110-119.

[9] Ledoit O, Wolf M.Nonlinear shrinkage estimation of large-dimensional covariance matrices [J]. The Annals of Statistics, 2012,40(2):1024-1060.

[10] Ledoit O, Wolf M.Optimal estimation of a large-dimensional covariance matrix under Stein's loss [J]. Working Paper, University of Zurich,2014.

[11] Ledoit O, Wolf M.Spectrum estimation: A unified framework for covariance matrix estimation and PCA in large dimensions [J]. Journal of Multivariate Analysis, 2015,139:360-384.

[12] Bollerslev T, Engle R F, Wooldridge J M.A capital asset pricing model with time-varying covariances [J]. The Journal of Political Economy, 1988,96(1):116-131.

[13] Engle R F, Kroner K F.Multivariate simultaneous generalized ARCH [J]. Econometric theory, 1995,11(1): 122-150.

[14] Engle R.Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models [J]. Journal of Business & Economic Statistics, 2002,20(3):339-350.

[15] Ledoit O, Santa-Clara P, Wolf M.Flexible multivariate GARCH modeling with an application to international stock markets [J]. Review of Economics and Statistics,2003, 85(3):735-747.

[16] Cappiello L, Engle R F, Sheppard K.Asymmetric dynamics in the correlations of global equity and bond returns [J]. Journal of Financial Econometrics, 2006,4(4): 537-572.

[17] Engle R, Kelly B.Dynamic equicorrelation [J]. Journal of Business & Economic Statistics, 2012,30(2):212-228.

[18] 刘志东,薛莉. 金融市场高维波动率的扩展广义正交GARCH模型与参数估计方法研究[J]. 中国管理科学, 2010, 18(6):33-41.

[19] 刘丽萍, 马丹, 白万平. 大维数据的动态条件协方差阵的估计及其应用[J]. 统计研究, 2015, 32(6):105-112.

[20] 张贵生, 张信东. 基于近邻互信息的SVM-GARCH股票价格预测模型研究[J]. 中国管理科学, 2016, 24(9):11-20.

[21] Hafner C M, Reznikova O.On the estimation of dynamic conditional correlation models [J]. Computational Statistics & Data Analysis, 2012,56(11):3533-3545.

[22] Engle R F, Shephard N, Sheppard K.Fitting and testing vast dimensional time-varying covariance models [R].Working Paper,New York University,2007.

[23] Engle R, Mezrich J. Garch for groups: A round-up of recent developments in Garch techniques for estimating correlation [J]. Risk: Managing Risk in the World's Financial Markets, 1996,9(8): 36-40.

[24] Stein C.Estimation of a covariance matrix [R]. Conference Paper,Rietz Lecture,1975.

[25] Stein C.Lectures on the theory of estimation of many parameters [J]. Journal of Soviet Mathematics,1986,34(1):1373-1403.

[26] Silverstein J W, Choi S I.Analysis of the limiting spectral distribution of large dimensional random matrices[J]. Journal of Multivariate Analysis, 1995,54:295-309.

Nonlinear Shrinkage Estimation of High Dimensional Conditional Covariance Matrix and its Application in Portfolio Selection

ZHAO Zhao

(School of Economics, Huazhong University of Science and Technology, Wuhan 430074, China)

It is well known that the traditional maximum likelihood estimation of GARCH model is severely biased in high dimensions. In this paper, the nonlinear shrinkage method proposed by Ledoit and Wolf is used to estimate DCC and BEKK models. In particular, the initial sample covariance estimator in maximum m-profile quasi-likelihood estimation (MMLE) proposed by Engle et al. is substituted by the nonlinear shrinkage estimator, which turns out to largely improve the estimation efficiency of high dimensional DCC and BEKK models, and for the first time, makes the valid estimation possible when the sample size is larger than the time series dimension. Based on the Percentage Relative Improvement in Average Loss (PRIAL), the Monte-Carlo simulations verify the obvious superiority of the nonlinear shrinkage substitution over the usual DCC and BEKK, which even strengthens as the ratio between sample size and time series dimension increases. Besides, for both DCC and BEKK, the performance of nonlinear shrinkage estimation is better than that of linear shrinkage, while linear shrinkage estimation is better than the usual estimation. Furthermore, the performance of DCC is better than BEKK, and the optimizing effect of nonlinear shrinkage on DCC is more significant than on BEKK. Finally, in the empirical part, using daily stock return data from the Center for Research in Security Prices (CRSP), the global minimum variance (GMV) portfolios of stocks traded in NYSE and NASDAQ are constructed based on various methods, and their real variances are compared. The empirical result supports the important role nonlinear shrinkage plays in promoting the estimation of high dimensional conditional covariance matrix, and thus in optimizing the portfolio selection.

nonlinear shrinkage；linear shrinkage；conditional covariance matrix

1003-207(2017)08-0046-12

10.16381/j.cnki.issn1003-207x.2017.08.006

2016-08-12；

2016-12-26

国家自然科学基金面上资助项目(71671070)

赵钊(1990-)，女(汉族)，湖北荆州 人，华中科技大学经济学院博士后，研究方向：金融资产组合理论与实证，E-mail:zhao.zhao@hust.edu.cn.

F224.0;F830.59

A