Smarandache函数的一类均值计算

马云真,李江华

(西安理工大学理学院,陕西 西安 710058)

Smarandache函数的一类均值计算

马云真,李江华

(西安理工大学理学院,陕西 西安 710058)

主要利用初等及解析方法研究F.Smarandache可乘函数¯S(n)的一类均值分布,并给出了该函数在k次根取整序列ak(n)上的均值渐近公式.

F.Smarandache可乘函数;均值;渐近公式

1 引言及结论

设n为任意正整数,F.Smarandache可乘函数f(n)的定义为：如果f(1)=1,当n＞1且时,有

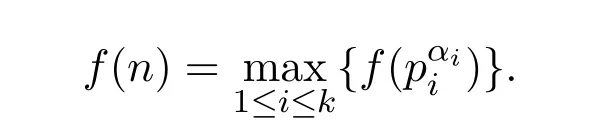
其著名的Smarandache函数

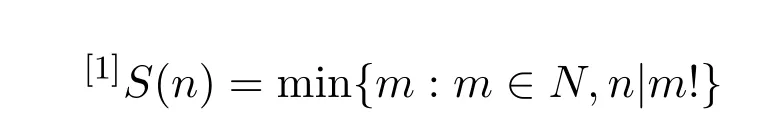
就是一个F.Smarandache可乘函数.由S(n)的定义,容易推断出如果

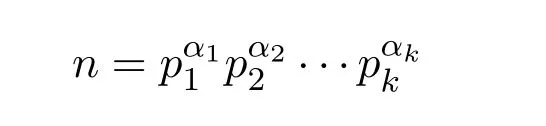
是n的标准分解式,那么

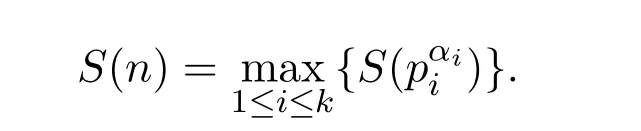
于是,S(n)是F.Smarandache可乘函数.关于S(n)的算术性质,有不少学者进行过研究,获得了许多有重要理论价值的研究成果,参阅文献[2-8].例如,Farris Mark和Mitchell Patrick在文献[2]中研究了S(n)的有界性问题,得出了S(pα)的上下界估计,即就是证明了：

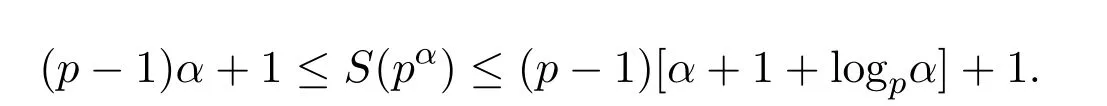
在文献[6]中,张利霞,赵西卿等人研究了数论函数S(SL(n))=φ(n)的可解性问题,也就是证明了下面的定理,即方程

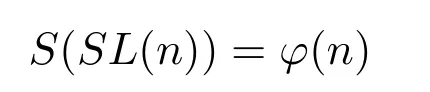
有且仅有n=1,8,9,12,18的解.其中SL(n)为F.Smarandache LCM函数,即

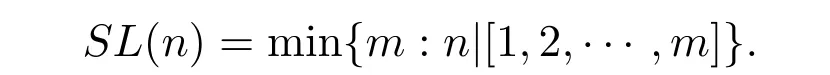
在文献[7]中,高丽和马娅锋主要研究了包含Smarandache幂函数的数论函数S(SP(n))的均值问题,也就是证明了下面的两个定理,即

对任意的实数x＞1,有

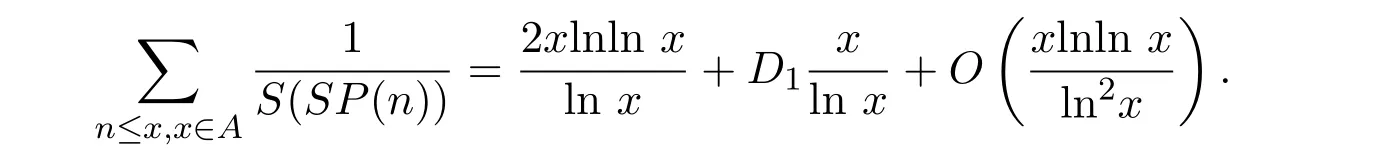
对任意的实数x＞1,有

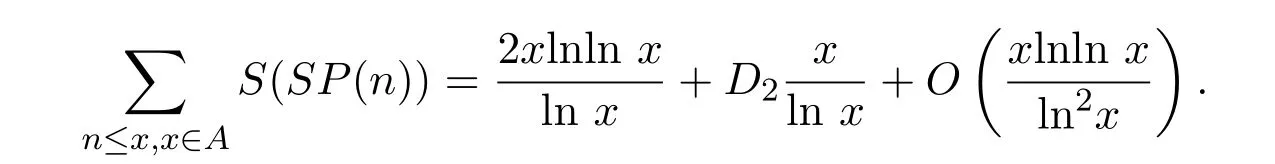
其中A为简单数集合,

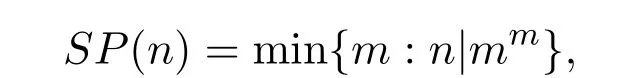
D1,D2为可计算常数.

在文献[8]中研究了S(n)的均值分布问题,获得了一个更深刻的结果,即就是证明了下面的定理：

设P(n)表示n的最大素因子,则对任意实数x＞1,有渐近公式：

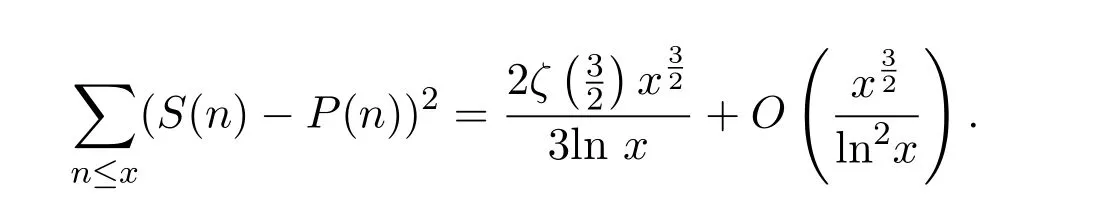
其中：ζ(s)为Riemann zeta函数.

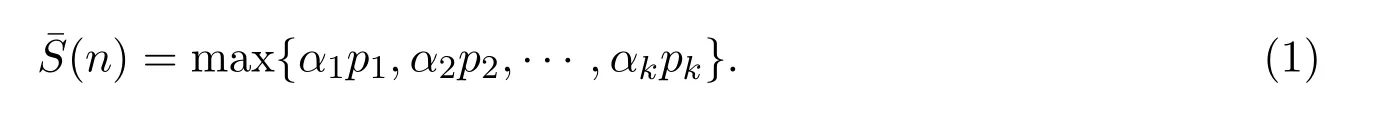
容易验证这个函数是F.Smarandache可乘函数.关于它的初等性质,不少学者已进行过研究,参见文献[8].文献[9]中还证明了下面的结论：设k为任意正整数,那么对任意实数x＞1,有渐近公式：

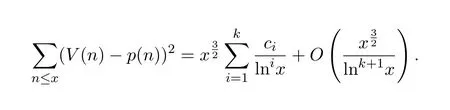
其中

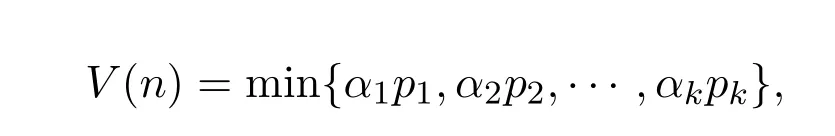
p(n)表示n的最小素因子,ci(i=2,3,...,k)为可计算的常数且

另外,对任意给定的正整数k,令ak(n)是n的k次根整数部分[1],即就是

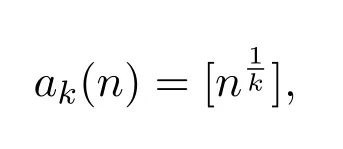
其中[x]表示小于或等于x的最大整数.例如,

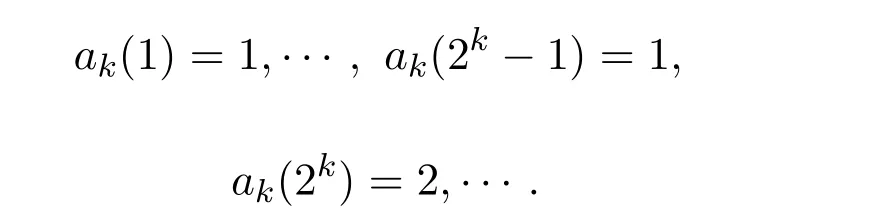
在正整数的k次根取整序列ak(n)上的分布性质.并给出一个较强的渐近公式.具体地说也就是证明下面：

定理 1.1对任意的实数x＞1,有渐近公式

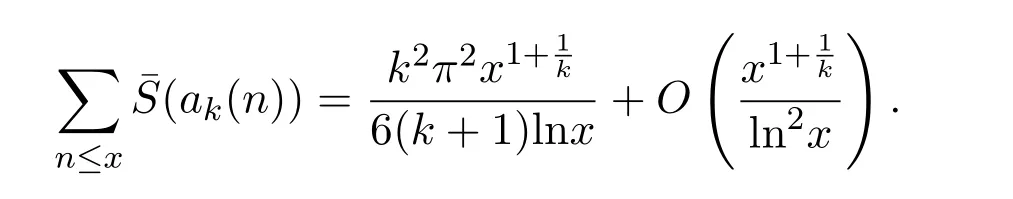
2 引理

为了完成定理的证明,需要如下几个简单的引理.首先令

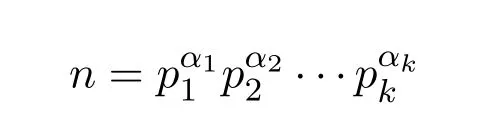
是n的标准分解式,P表示n的最大素因子,即就是

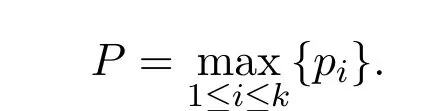
那么有

引理 2.1对任意的实数x＞1,有渐近公式

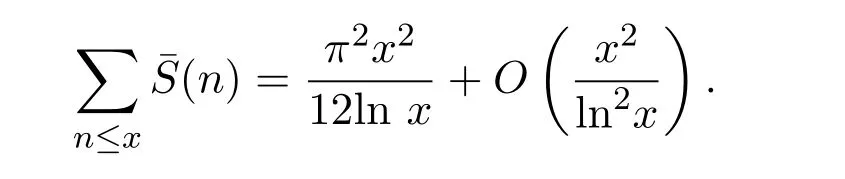
证明首先定义如下两个集合A和B：

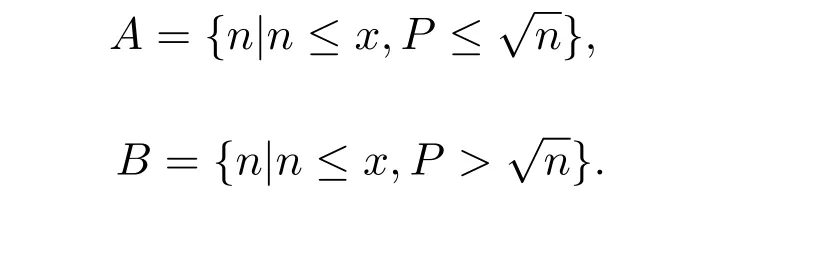
应用Euler求和公式[10],可得

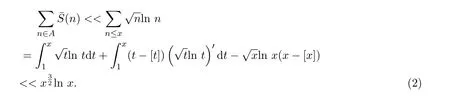
类似地,对集合 B,由Abel恒等式[10],有

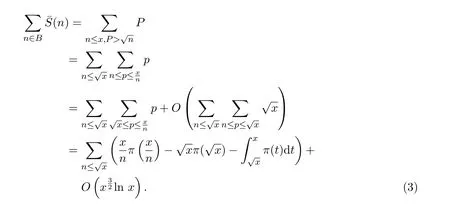
其中,π(x)表示所有不超过x的素数个数，注意到

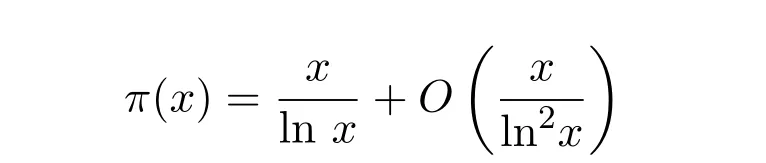
根据Abel恒等式,可得

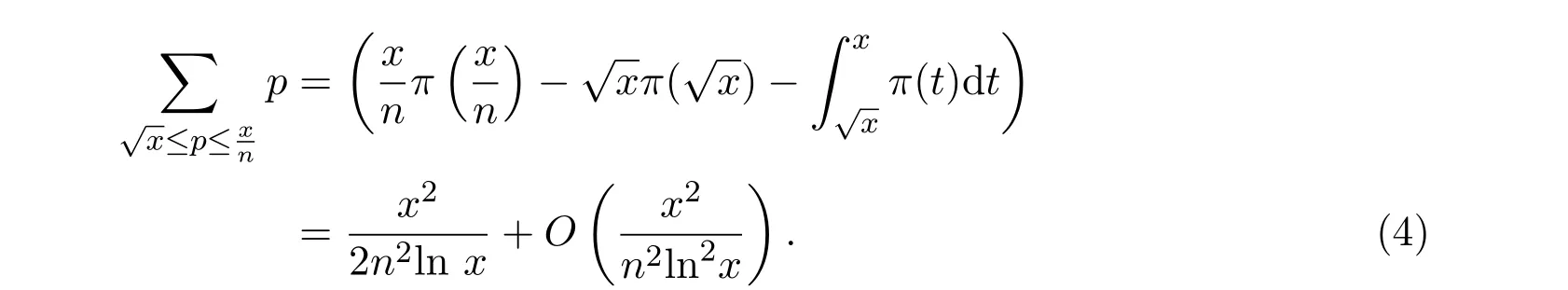
又因为

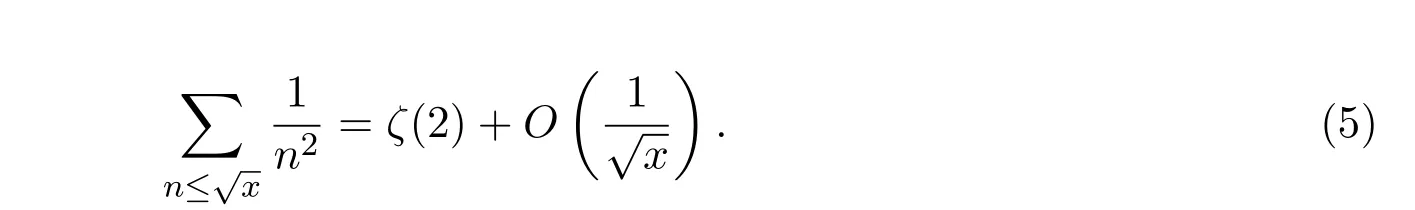
综合(2),(3),(4)和(5),即可得到引理2.1的结果.

引理 2.2对任意正整数k和非负整数i,有渐近公式

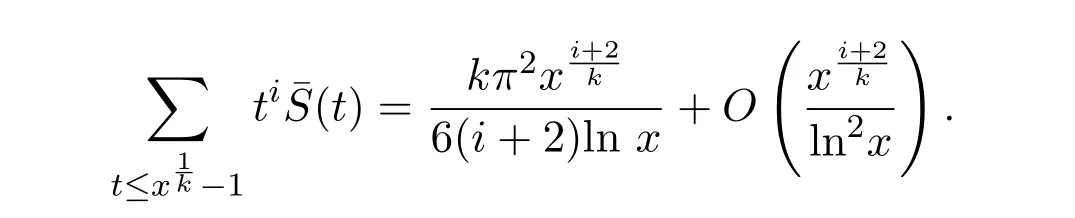
证明结合引理2.1,并应用Abel恒等式,

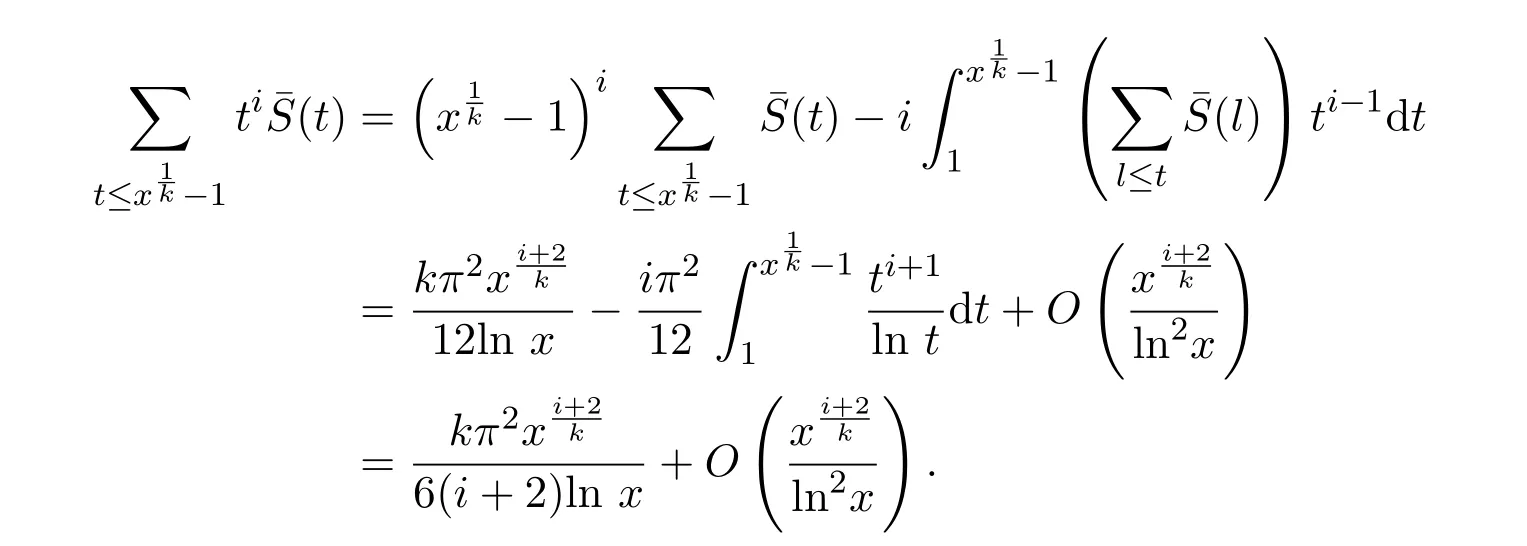
引理2.2得证.

3 定理的证明

定理的证明.

证明首先,对任意实数x≥1,设M 为一个给定的正整数使得

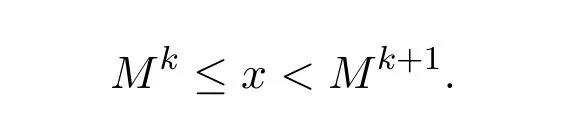
于是完成了定理的证明.

致谢：衷心地感谢马茂元教授和刘二女教授的支持与鼓励！

参考文献

[1]Smarandache F.Only Problems,Not Solutions[M].Chicago：Xiquan Publishing House,1993.

[2]Farris Mark,Mitchell Patrick.Bounding the Smarandache function[J].Smarandache Notions Journal,2002,13(2)：37-42.

[3]Lu Yaming.On the solutions of an equation involving the Smarandache function[J].Scientia Magna,2006,2(1)：76-79.

[4]Jozsef Sandor.On certain inequalities involving the Smarandache function[J].Scientia Magna,2006,2(3)：78-80.

[5]Liu Yanni,Pan Xiaowei.Two equation involving the Smarandache function and its solutions[J].黑龙江大学自然科学学报,2006,23(6)：857-858.

[6]张利霞,赵西卿,郭瑞,等.关于数论函数S(SL(n))=φ(n)的可解性[J].纯粹数学与应用数学,2015,31(5)：533-536.

[7] 高丽,马娅锋.包含Smarandache幂函数的均值问题[J].纺织高校基础科学学报,2016,29(1)：8-10.

[8] 徐哲峰.Smarandache函数的值分布性质[J].数学学报,2006,49(5)：1009-1012.

[9]沈虹.一个新的数论函数及其它的值分布[J].纯粹数学与应用数学,2007,23(2)：235-238.

[10]潘承洞,潘承彪.解析数论[M].北京：北京大学出版社,2003：22-25.

On the mean value of Smarandache function

Ma Yunzhen,Li Jianghua
(College of Science,Xi′an University of Technology,Xi′an 710058,China)

The main purpose of this paper is using the elementary method and analytic method to study the mean value of the F.Smarandache multiplicative function,and give an asymptotic formula of F.Smarandache in positive integer′s k-th root.

F.Smarandache multiplicative function,mean value,asymptotic formula

O156.4

A

1008-5513(2017)04-0424-06

10.3969/j.issn.1008-5513.2017.04.009

2017-04-17.

陕西省自然科学基金(2017JQ1020).

马云真(1989-),硕士生,研究方向：解析数论及其应用.

李江华,博士,副教授,研究方向：解析数论及其应用.

2010 MSC：11B83