关于模糊数序列收敛性问题的研究

赵博,包玉娥

(内蒙古民族大学数学学院,内蒙古 通辽 028043)

关于模糊数序列收敛性问题的研究

赵博,包玉娥

(内蒙古民族大学数学学院,内蒙古 通辽 028043)

讨论了模糊数序列在EW-型积分度量下的收敛性问题.首先给出了模糊数序列关于EW-型积分度量、水平EW-型度量以及水平EW-型测度收敛的概念;其次,讨论了模糊数序列关于EW-型积分度量、下方图度量以及水平度量收敛之间的关系,证明了在一定条件下模糊数序列关于EW-型积分度量、下方图度量以及水平度量收敛的等价性.

模糊数序列;下方图度量;EW-型积分度量;收敛性

1 引言

模糊数是实数域上的一类特殊的模糊集,在模糊分析学及其应用研究中起着非常重要的作用.在实际应用中,经常用模糊数来表示属性决策领域中的许多决策信息[12].根据实际问题的需要,人们为了更好的研究模糊分析及其应用问题,在模糊数空间上定义了各种各样的度量[3].从此,人们开始讨论了模糊数空间的分析性质,给出了模糊数序列在各种度量之下的收敛性概念,为模糊分析及其应用问题的研究打下了良好的基础[47].

区间数和模糊数的应用实际上均为属性值为实数的信息系统在维度上的化简,并且模糊数又可以用一族区间数来刻画.文献[910]中,建立了区间数空间上的EW-型积分度量及EW-型贴近度等概念,得到了一些有意义的结论.本文讨论模糊数序列在EW-型积分度量之下的收敛性问题.

2 基本概念

设R为实数集.如果模糊集u：R→[0,1]是正规的,凸的上半连续的,且支集是紧集,则称u为模糊数.模糊数全体构成的空间称为模糊数空间,记为F0.

对于u∈F0,称

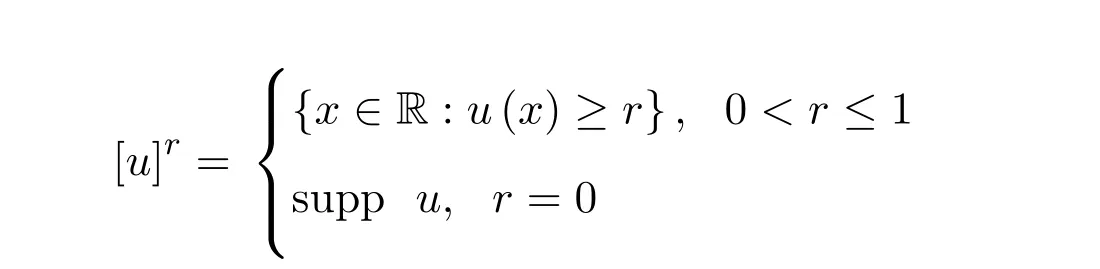
为模糊数u的r-截集或r-水平集.

对任意的r∈[0,1],模糊数u的r-截集[u]r是实数集R上的一个非空有界闭区间.记为

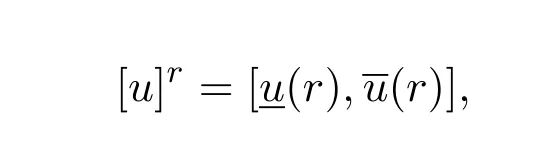
在F0上的序关系定义为：

对于u,v∈F0及k∈R,模糊数空间上的加法和数乘运算定义为：

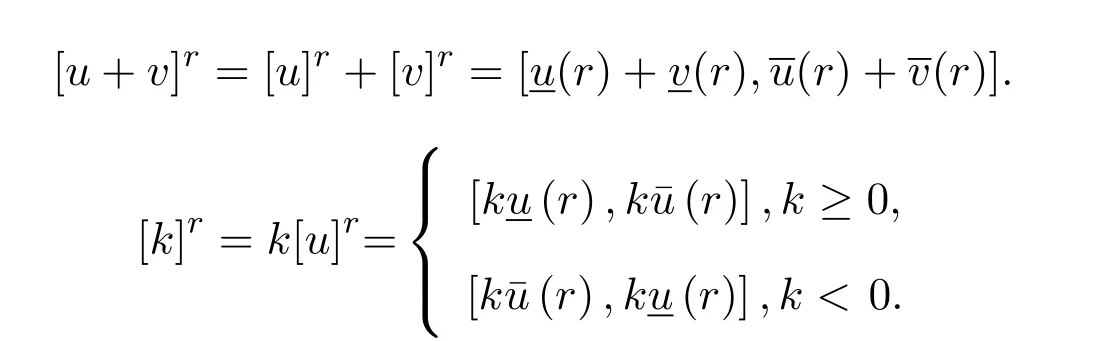
定义 2.1设(X,dH)是一个度量空间,A,B是X中的两个非空紧集,则称

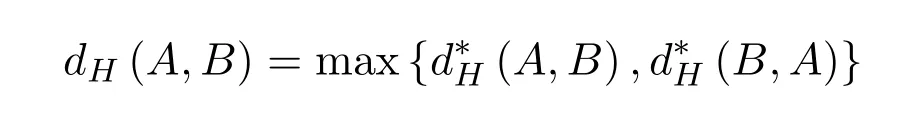
为A和B的Hausdor ff度量,其中

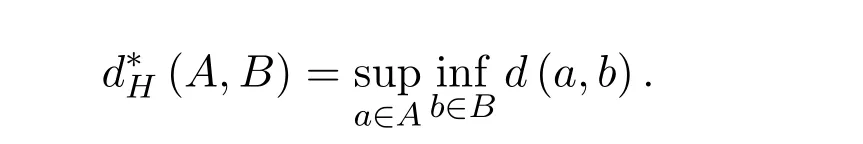
定义 2.2[3]设u,v∈F0,则称

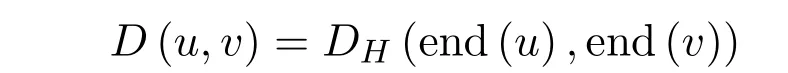
为模糊数空间F0上的下方图度量.其中

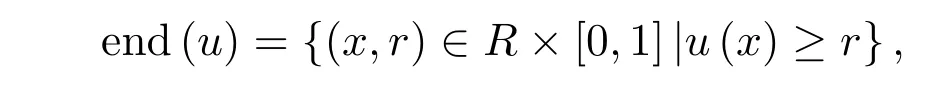
DH为定义R2在上的紧集族的Hausdor ff度量.

定义 2.3[3]设 uk,u ∈ F0(k=1,2,...),如果

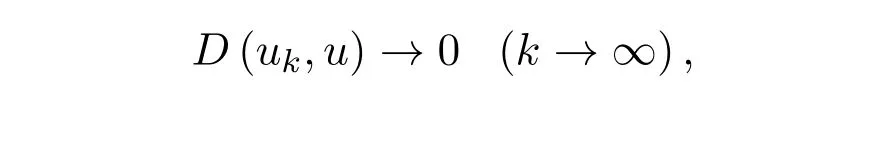
则称模糊数序列{uk}依下方图度量收敛于模糊数u,记为

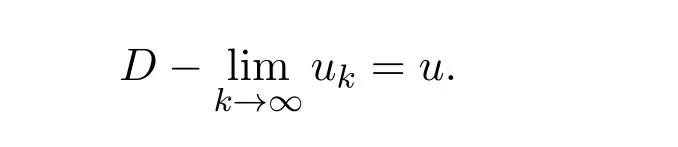
定义 2.4[6]设 uk,u∈F0(k=1,2,...),如果对于任意的 r∈[0,1],有

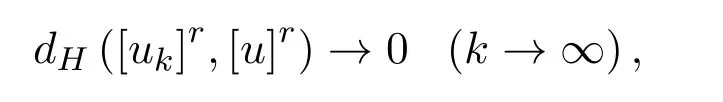
则称模糊数序列{uk}依水平Hausdor ff度量收敛于模糊数u,记作

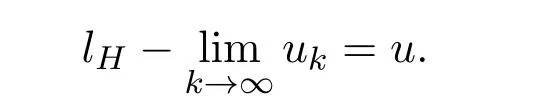
定义 2.5[6]设 uk,u ∈ F0(k=1,2,...),如果

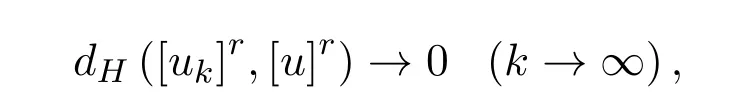
关于r在[0,1]上几乎处处成立,则称模糊数序列{uk}依水平Hausdor ff度量几乎处处收敛于模糊数u.

引理 2.1[6]若 uk,u∈F0(k=1,2,...),则以下结论等价：

(2)模糊数序列{uk}依Hausdor ff度量dH水平几乎处处收敛于模糊数u;(3)对所有

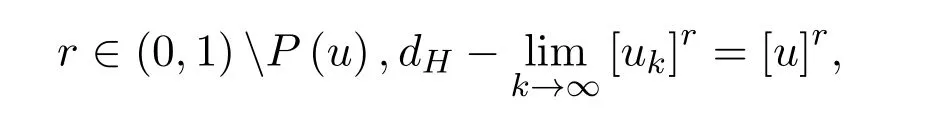
其中

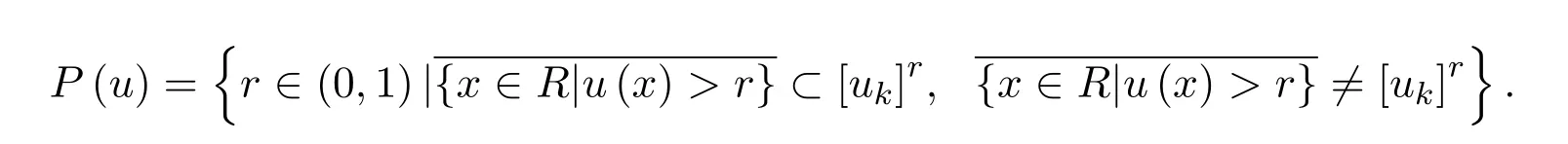
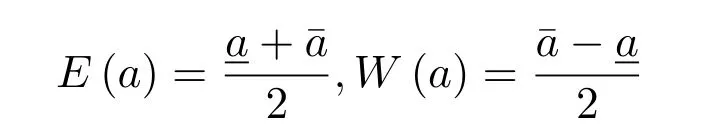
分别为区间数的期望值与宽度.

定理 2.1[9]设u,v∈F0,映射

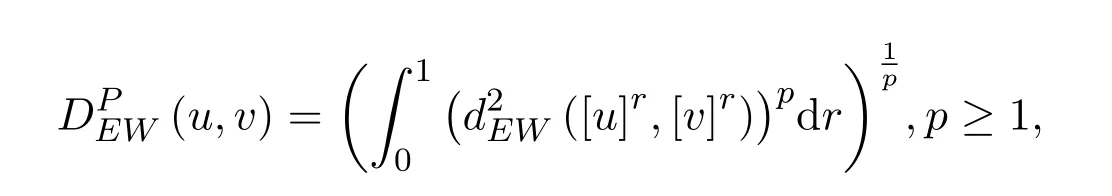
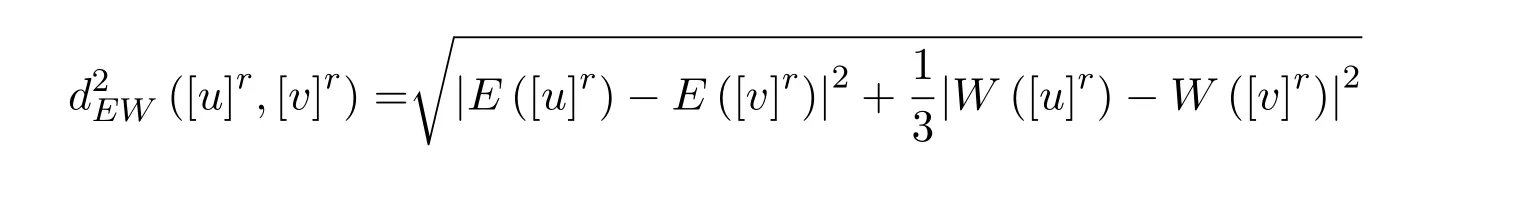
为区间数空间[R]上的EW-型度量.

定理2.2[10]设

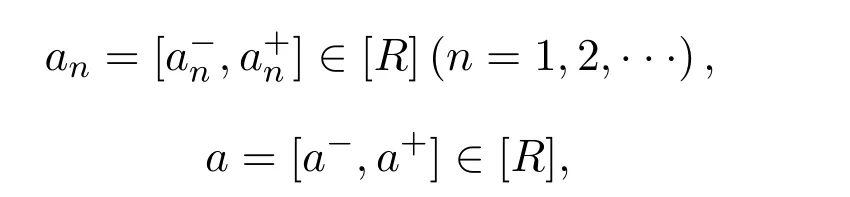
则区间数序列{an}依EW-型度量收敛于区间数a,即

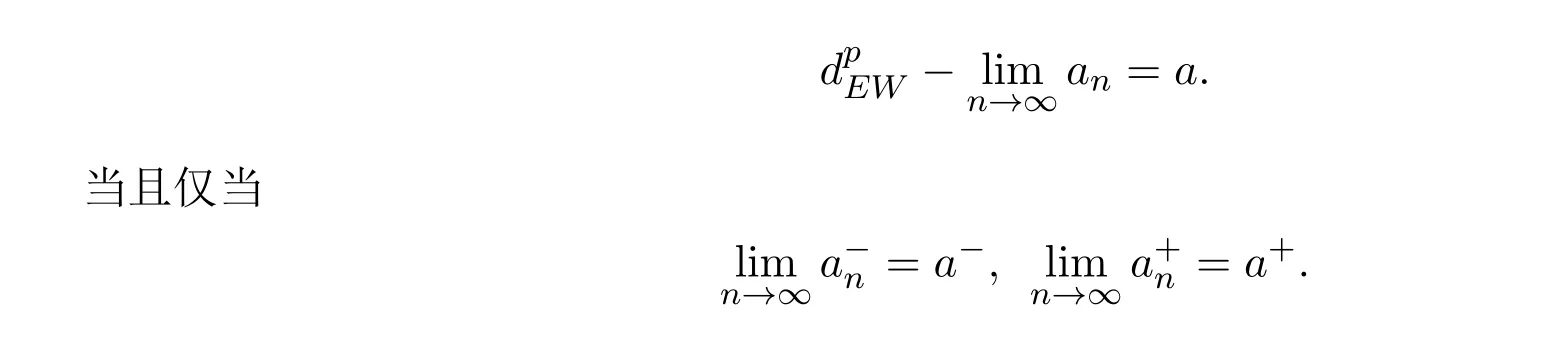
3 EW-型积分度量空间上的收敛性

定义 3.1设 uk,u∈ F0(k=1,2,...),如果

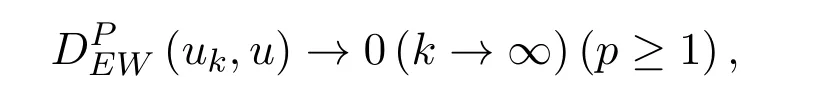
则称模糊数序列{un}依EW-型度量收敛于模糊数u,记作

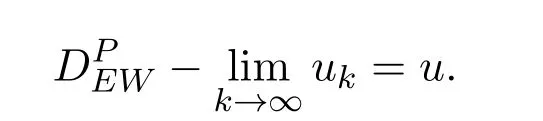
定义 3.2设 uk,u∈F0(k=1,2,...),如果对于任意的 r∈[0,1],有

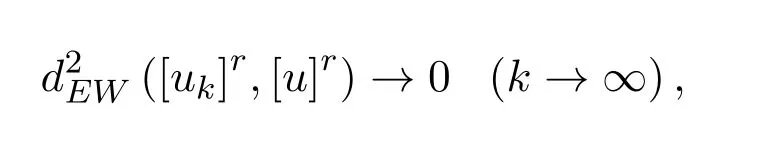
则称模糊数序列{uk}依水平EW-型度量收敛于模糊数u,记作

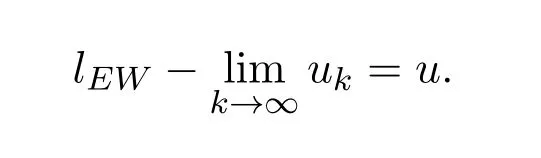
定义 3.3设 uk,u∈F0(k=1,2,...),如果对于任意的 ε＞0和 η＞0,存在 k＞0,使得当 k≥K 时,有

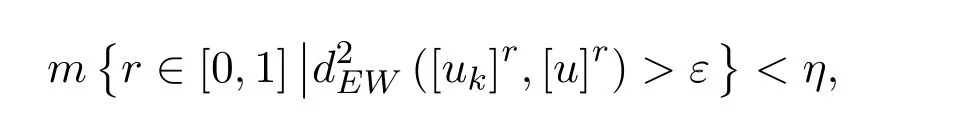
其中m表示实直线R上的Lebesgue测度,则称模糊数序列{uk}在EW-型度量下依测度收敛于模糊数u,记作

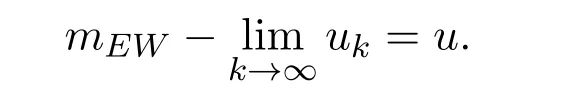
定理 3.1若uk,u∈F0(k=1,2,...),那么以下四个命题等价：

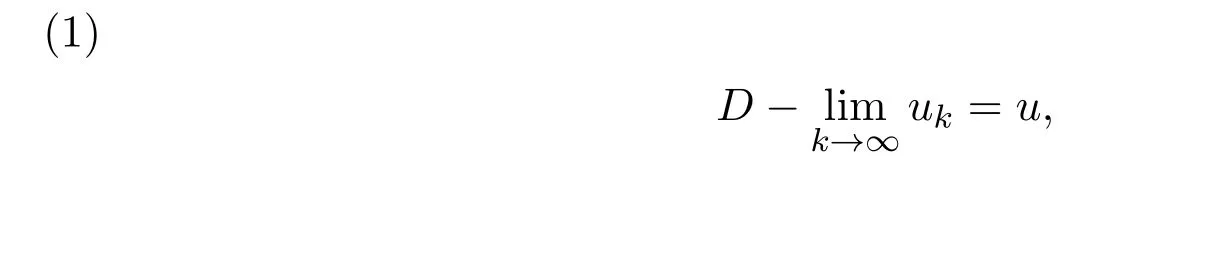
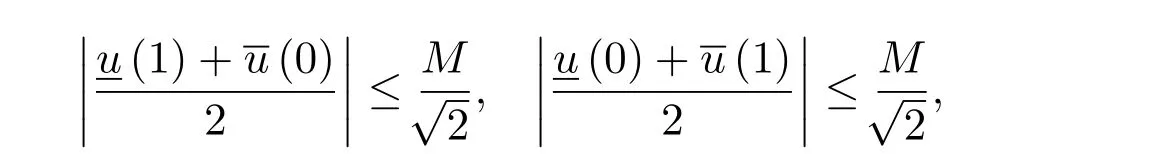
从而对任意的k＞0,有

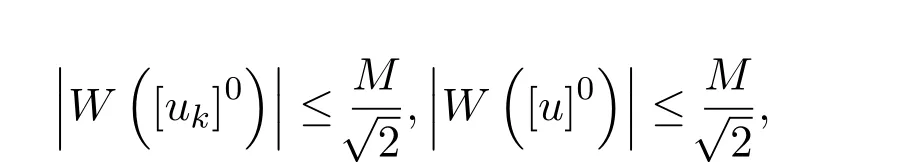
又对任意r∈[0,1],由 [uk]1⊂[uk]r⊂[uk]0及[u]1⊂[u]r⊂[u]0,有

又因为

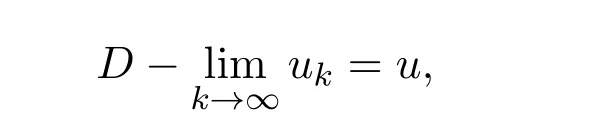
所以由引理 2.1,模糊数序列 {uk}依水平 Hausedor ff度量几乎处处收敛于u.从而由定义 2.5,在[0,1]中存在零测度集Ω,使得

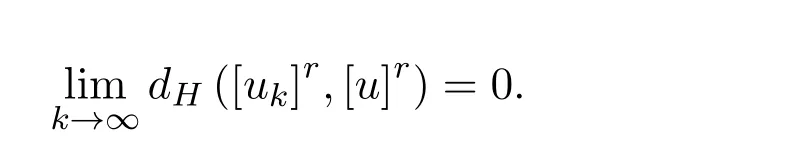
对任何r∈[0,1]Ω都成立.即

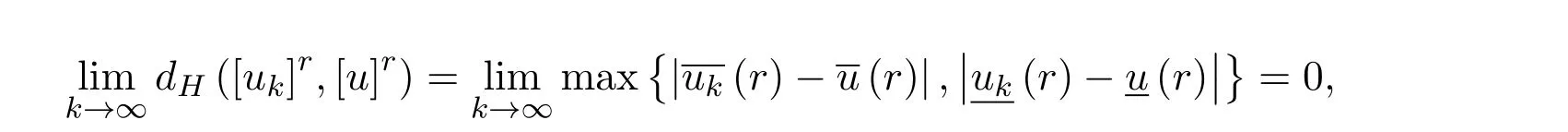
对任何r∈[0,1]Ω都成立.从而有

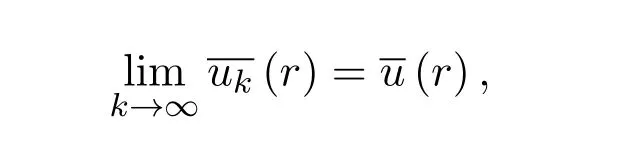
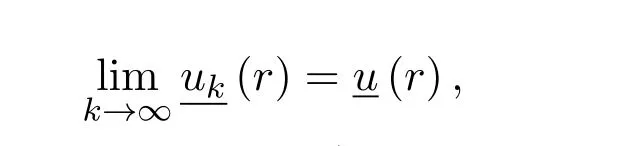
对任何 r∈[0,1]Ω都成立.于是对r∈[0,1]Ω,有

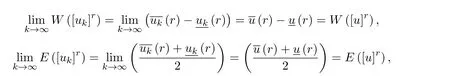
所以对 r∈[0,1]Ω,有

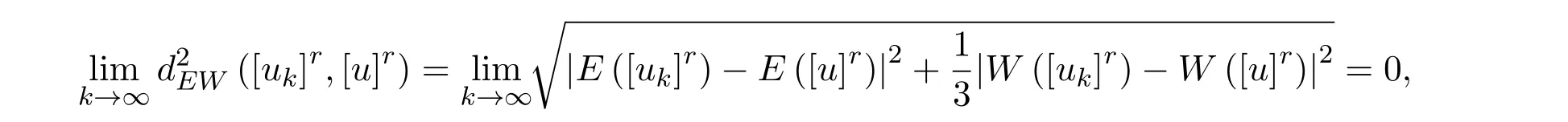
从而对任意的ε＞0,存在K＞0,使得当k＞K 时,有

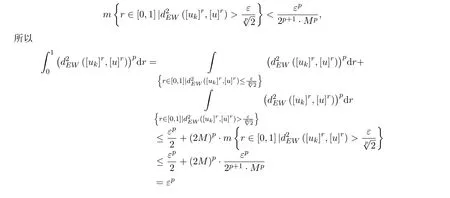
即对任意ε＞0,存在K＞0,使得当k＞K 时,有

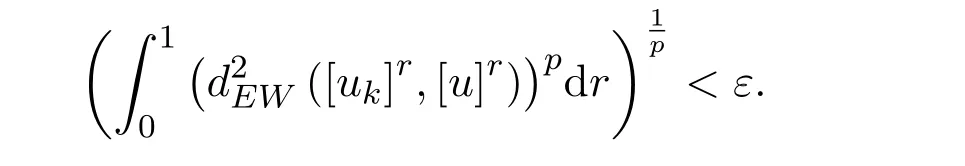
从而

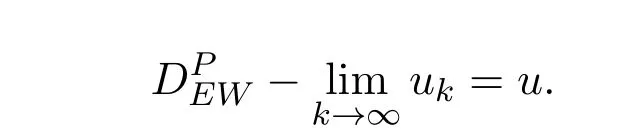
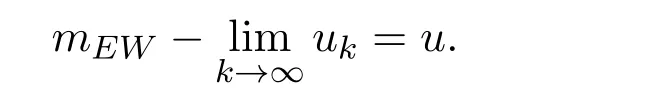
对任意ε＞0和η＞0,显然有

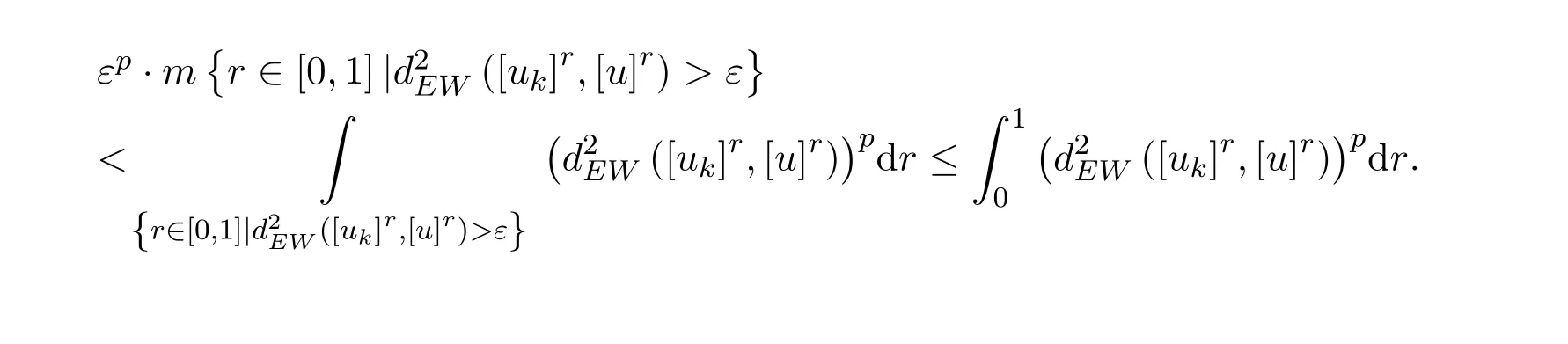
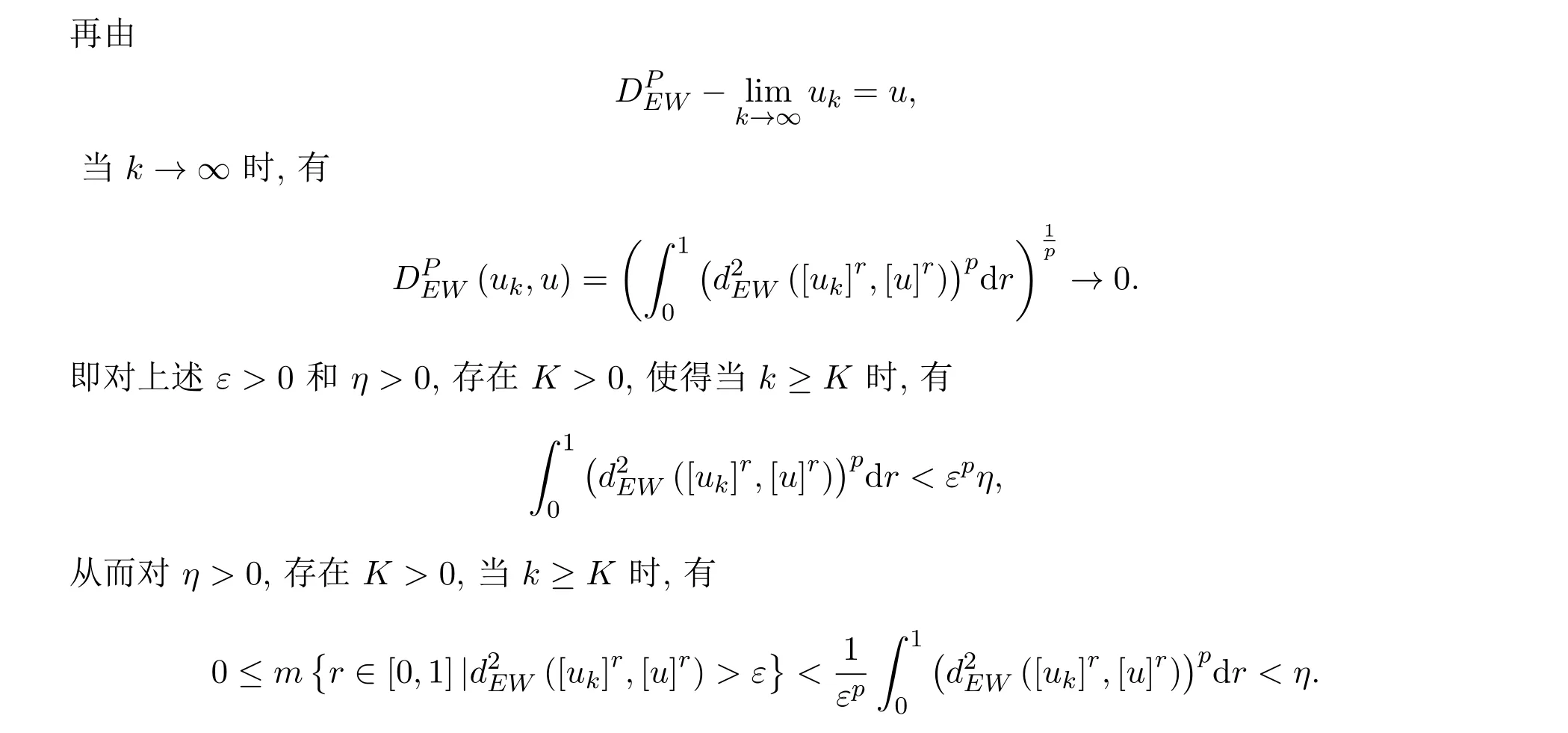
由定义 3.3,有

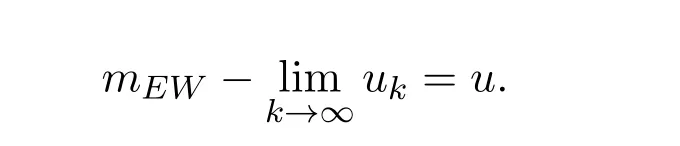
其次利用反证法证明

假设存在r0∈(0,1),使得 [uk]r0在度量之下不收敛于[u]r0,则存在 ε0＞0和自然数列{kj}使得

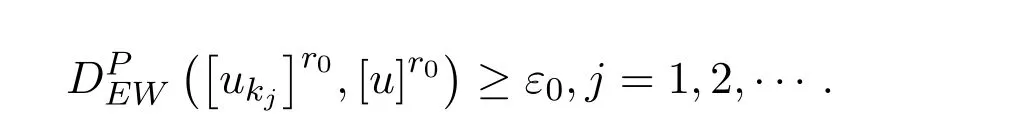
又由

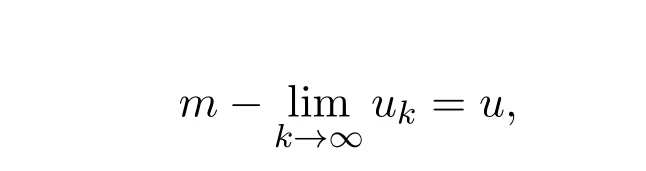
有

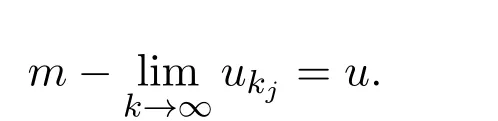
从而存在{ukj}的子列使得

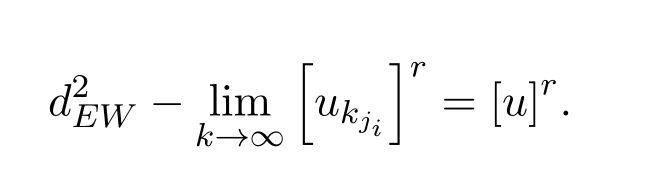
关于r在[0,1]上几乎处处成立.即存在Ω⊂[0,1]且m(Ω)=0满足

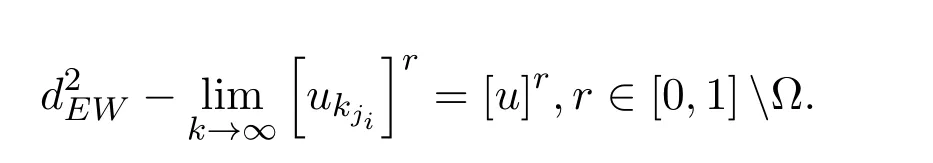
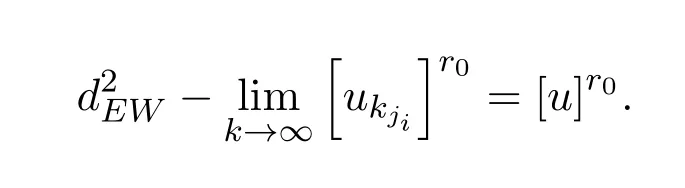
若r0∈Ω,则由u∈F0可知,对上述ε0＞0,存在对任意kji,有

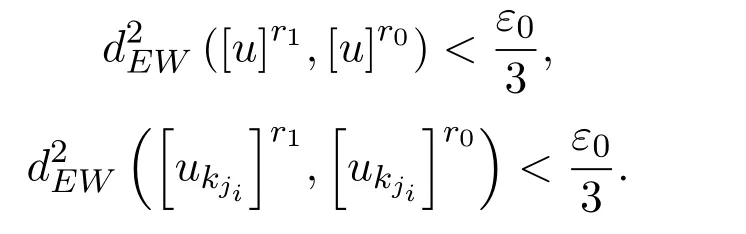
对上述r1/∈Ω,存在K′＞0,当i≥K′时,有

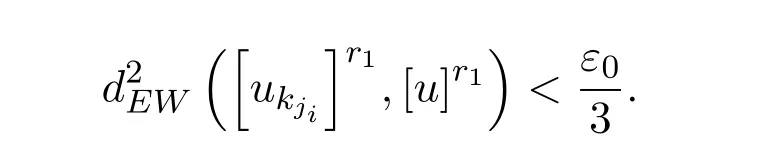
从而当 i≥K′时,有

即

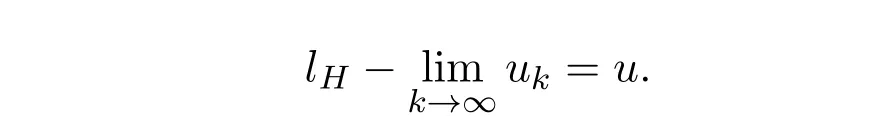
(4)⇒(1)根据下方图度量的定义2.2,有

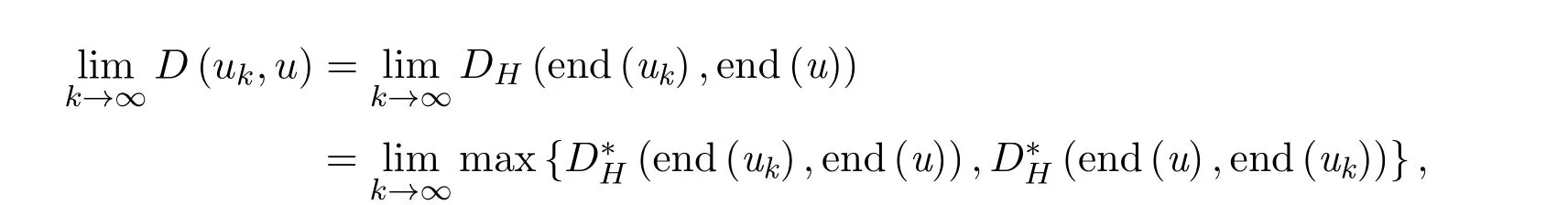
其中

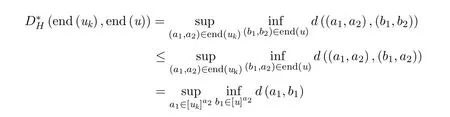
参考文献

[1]兰蓉,范九伦.三角模糊数上的完备度量及其在决策中的应用[J].统工程学报,2010,3：314-319.

[2]Chen S M,Cheng S H,Lan T C.A novel similarity measure between intuitionistic fuzzy sets based on the centroid point so ftrans formed fuzzy numbers with applications to pattern cognition[J].Information Sciences,2016,344：15-40.

[3]Diamond P,Kloeden P.Metric Spaces of Fuzzy Sets：Theory and Applications[M].London：World Scienti fi c Publishing,1994.

[4]Wu C X,Wang G X.Convergence of sequence of fuzzy numbers and 1xed point theorems for increasing fuzzy mappings and application[J].Fuzzy Sets and Systems,2002,130：383-390.

[5]Fang J X,Huang H.On the level convergence of a sequence of fuzzy numbers[J].Fuzzy Sets and Systems,2004,147：417-435.

[6]Wu C X,Li H L,Ren X K.A note on the sendograph metric of fuzzy numbers[J].Information Sciences,2009,179：3410-3417.

[7]Huan H,Wu C X,Xie J L,et al.Approximation of fuzzy numbers using the convolution method[J].Fuzzy Sets and Systems,2017,310：14-46.

[8]雷一鸣,包玉娥.关于模糊数贴近度问题的研究[J].纯粹数学与应用数学,2015,6：611-619.

[9]包玉娥,雷一鸣.模糊数空间上的积分度量及其在模糊聚类中的应用[J].模糊系统与数学,2017,4：133-139.

[10]包玉娥,彭晓芹,赵博.基于期望值与宽度的区间数距离及其完备性[J].模糊系统与数学,2013,6：133-139.

Study on the convergence problem of fuzzy number sequence

Zhao Bo,Bao Yu-e
(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China)

In this paper,we discusses the convergence problem of the fuzzy number sequence on theEW-type integral metric.First we give the concept of the fuzzy number sequence ofEW-type integral metric,LevelEW-type metric and LevelEW-type metric convergence;Second,Discusses the relationship among the fuzzy number sequence on theEW-type integral metric and The fi gure below metric and the convergence of Level metric,and then prove the equivalence among the fuzzy number sequence on theEW-type integral metric and The fi gure below metric and the convergence of Level metric.

the fuzzy number sequence,the fi gure below metric,theEW-type integral metric,convergence

O159.2

A

1008-5513(2017)04-0340-12

10.3969/j.issn.1008-5513.2017.04.002

2017-07-07.

国家自然科学基金(11461052).

赵博(1987-),硕士,讲师,研究方向：不确定性数学理论及应用.

2010 MSC:03E72