耦合 Schr¨odinger和 KdV 方程组孤波解的存在性
吴阿丽,魏公明
(上海理工大学,上海市 200093)
耦合 Schr¨odinger和 KdV 方程组孤波解的存在性
吴阿丽,魏公明
(上海理工大学,上海市 200093)
主要研究了耦合的非线性 Schrdinger和 KdV方程孤波解的存在性.文章利用集中紧性原理找到预紧性的极小化序列,通过平移的方式来寻找方程组对应泛函在H1(R)的极小值函数,从而得到原方程非平凡解的存在性.
NLS-KdV方程组;极小化序列;对称重排;集中紧性原理
1 引言

和KdV方程

是色散介质中非线性波的经典模型.对于方程(2)的讨论.可参见文献[9-10,12].
本文的研究是受文献[1,4]的启发,在文献[1]中,作者研究了如下问题:
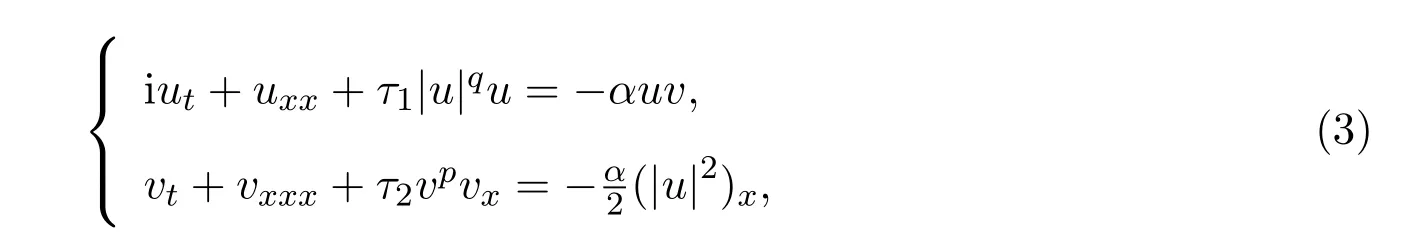
其中τ1,τ2和α都是实常数.在(3)中的耦合形式是比较常见的,该系统起源于大量的关于长波和长波长包络的短波交互作用的物理模型,详细可参阅文献[3,6].在文献[1]中,证明在

的约束下,其中 α>0,τ1>0,τ2>0和 1≤q<4,形如

孤立波解的存在性,其中c>0,ω∈R,而ϕ:R→C和ψ:R→R都是在无穷远处趋于零的函数.由文献[1]中对耦合项的条件限制,自然会想到可否进一步考虑更广泛类型的耦合的Schrdinger-KdV方程组呢?第一,可以将p和q耦合项u的的幂次项系数范围扩大.第二,将(3)推到更高维的模型.第三,把(3)中一个薛定谔方程和一个KdV方程的方程组推广到一个Schr¨odinger方程和多个KdV方程组或者是一个KdV方程和多个Schrdinger方程的方程组.从证明的技术上讲,推广的困难之处在于在证明次加性泛函的构造上,还有在构造时需要的重排不等式.本文受文献[4]的启发,将文献[5,11]的重排不等式的结果应用于排除二分性上.文献[5]中引理A.1将文献[1]中的重排不等式结果从一维推广到了任意维数.文献[4]研究了如下的非线性Schr¨odinger系统驻波的存在和稳定性,

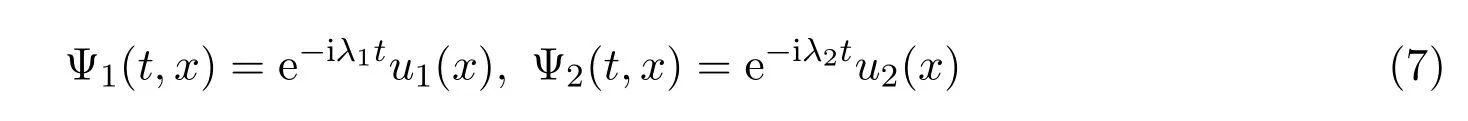
的孤波解的存在性和轨道稳定性:
受上述两篇文章的启发,本文主要研究如下的NLS-KdV方程组:

当 β>0,µi>0,1<r<5,2<pi<6,i=1,2时,形如
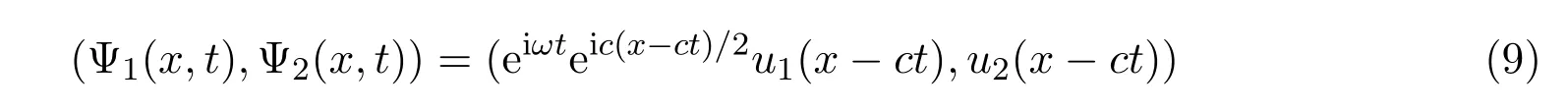
的孤波解的存在性和轨道稳定性.即研究如下方程组的非平凡解的存在性,
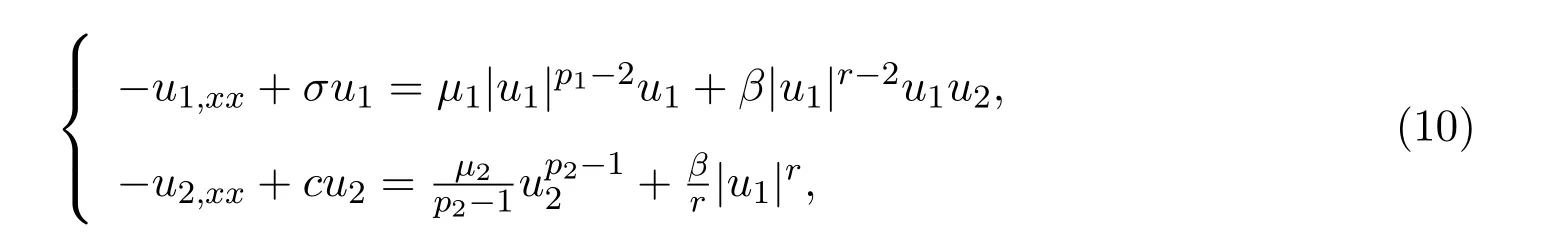
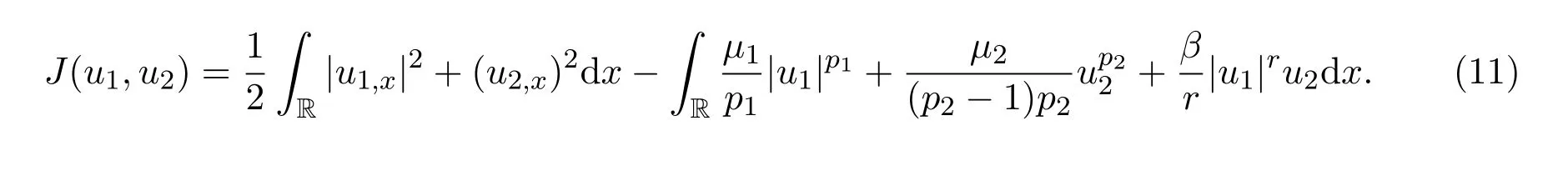
约束集是

从而极小化问题为
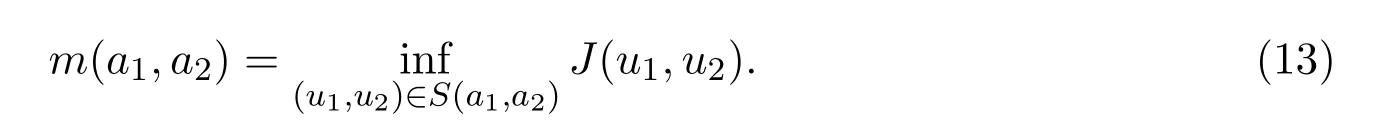
最后通过集中紧性原理来解决带约束的极小化问题.
注 1.1在这篇文章中和H1(R)分别代表H1(R)里复函数和实函数的集合.其范数是

对所有的1≤p<∞,Lp(R)是普通的Lebesgue空间,其范数是

定义符号→和⇀分别代表强收敛和弱收敛.并定义B(x,R)为在一维空间里面的以x为中心R为半径的开区间.
定理1.1 假设当
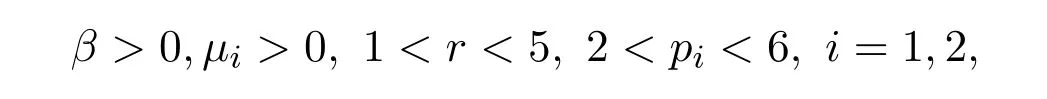
则对任意的a1>0和a2>0,m(a1,a2)可以被达到,即存在
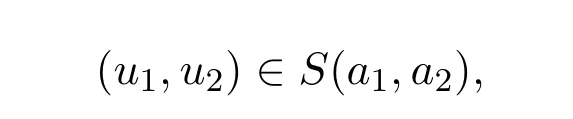
使得

论文的安排如下:第二节,介绍一些重要的预备引理.定理1.1将在第三节进行详细的证明.
2 预备结果

其中
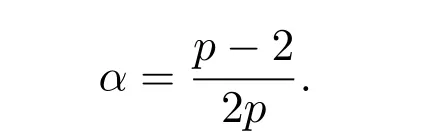
对1<r<5,存在一个q>1,使得

其中
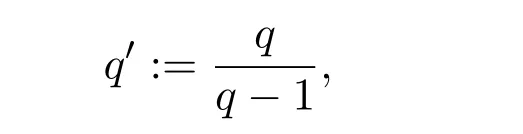

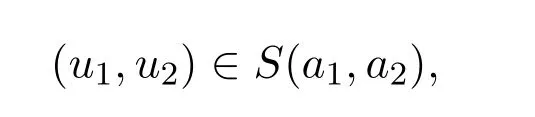
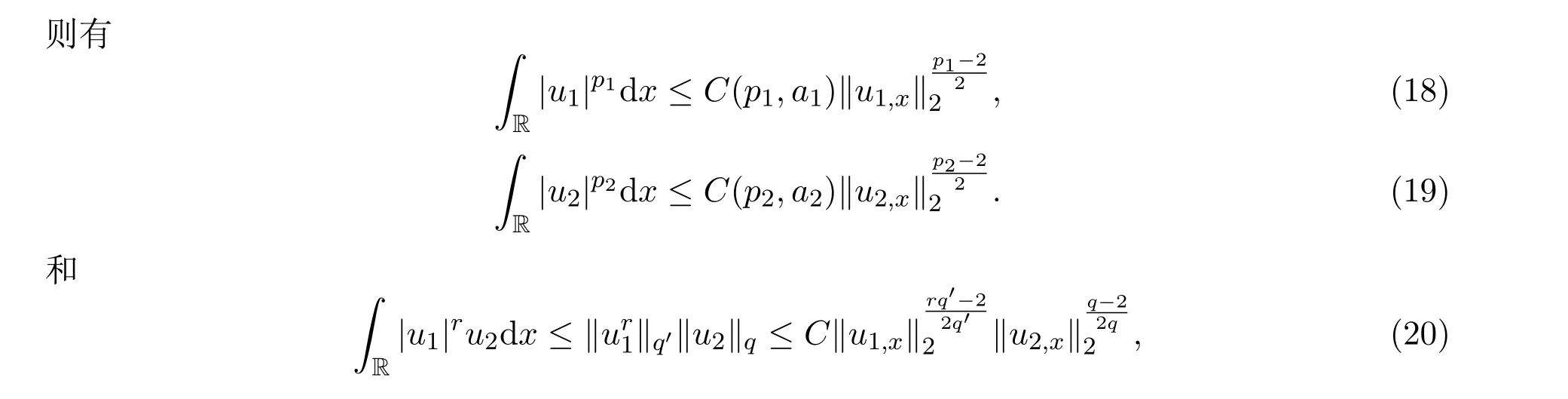
在接下来的主要定理证明中,在排除二分性时,需要文献[11]的重排结果,具体的证明可参阅文献[5].设u是一个在RN上的Borel可测函数.设A⊂RN是Lebesgue可测集,用|A|代表测度.设u,v是RN上在无穷远处有界的Lebesgue可测函数,对t>0,定义

其中r>0,由
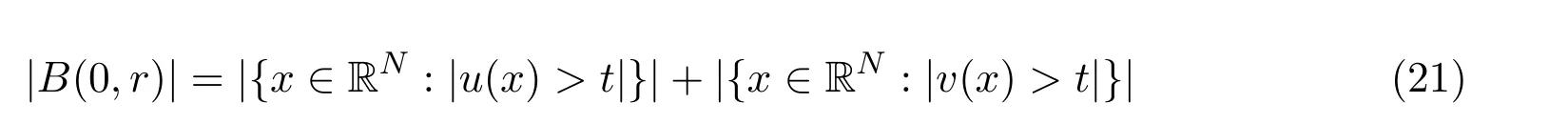
来确定.定义

其中χA(x)是集合A⊂RN的特征函数.
引理 2.1设u,v∈H1(RN),则
(i)函数{u,v}∗是径向对称的,非增和下半连续的.此外,对任意t>0有
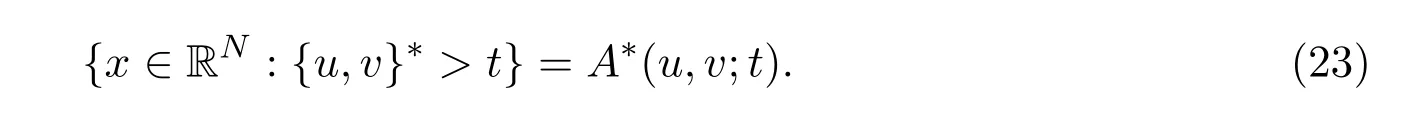
(ii)若Φ:[0,∞)→[0,∞)是非减,下半连续,在 0点连续和Φ(0)=0,则

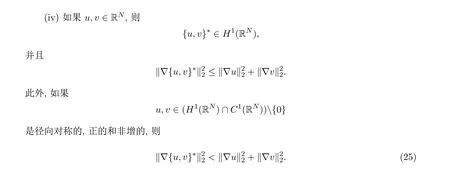
(v)若u1,u2,v1,v2≥0,是Borel可测函数并在无穷远处有界,则
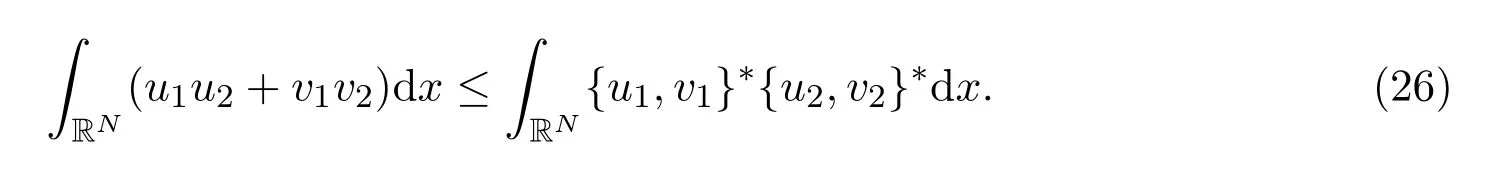
在本文中,利用Brezis-Lieb引理可以得到一些重要的极限关系.下面将先详细介绍下该引理的具体内容.
引理 2.2设Ω是RN的开子集和un⊂Lp(Ω),1≤p<∞.若
(1)un在 Lp(Ω)里有界;
(2)un在Ω里几乎处处收敛到u0;则
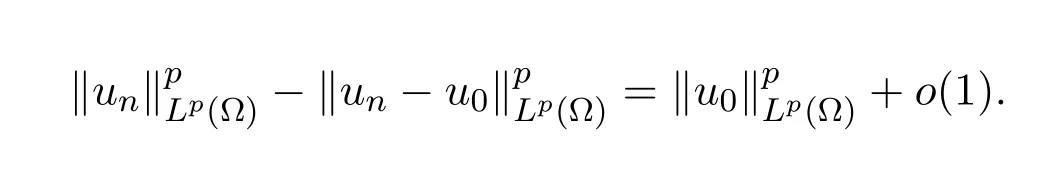
3 定理1.1的证明
为证明后面极小化序列经过平移具有紧性,我们先证明 m(a1,a2)和其极小化序列在的性质.
引理 3.1(i)对任意的a1,a2≥0,若a1>0或者a2>0,则

(ii)m(a1,a2)对a1,a2≥0是连续的.
(iii)对任意的a1≥b1≥0,a2≥b2≥0,有

证明(i)首先证明m(a1,a2)<0,任选一个(u1,u2)∈S(a1,a2)且u1,u2皆为非负函数,定义
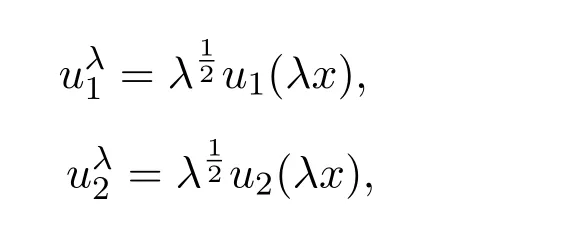
其中λ为任意大于0的数.则
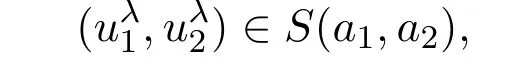
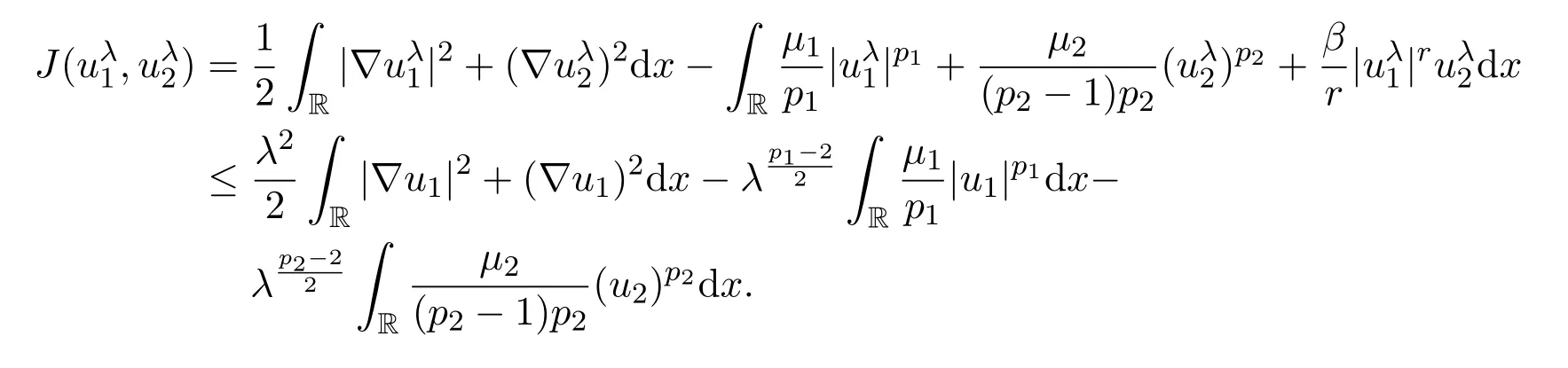



其中
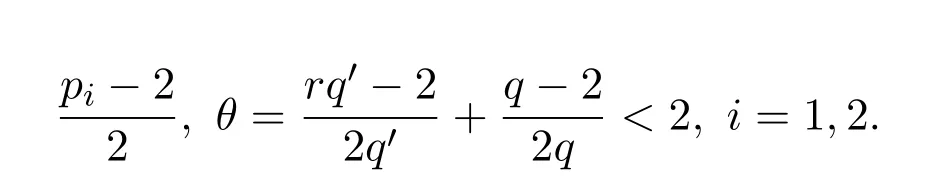
引理 3.2假设1<r<5.如果在里

则
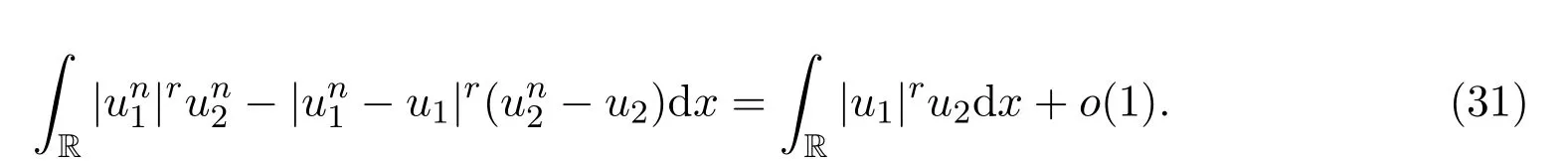
证明该引理的证明与参考文献 [4]相似.为了完整性,将提供具体证明过程.对任意b1,b2,c1,c2∈R和ε>0,利用平均值定理和Young不等式可得
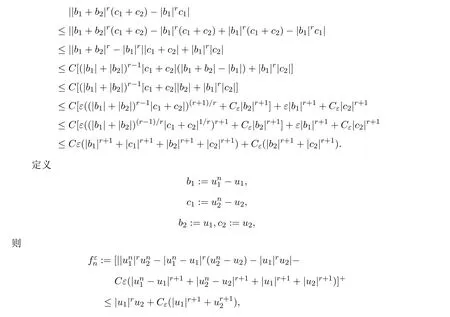
其中
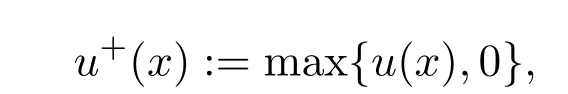
根据Lebesgue控制收敛定理得到

因为


引理 3.3对(13)的任意极小化序列通过平移,对2<p<6,在Lp(R)×Lp(R)里强收敛.
证明假设是定义在S(a1,a2)关于泛函J的极小化序列.由引理3.1(iv)可知序列在上是有界的.为了下文中研究泛函J性质的方便,由

因为

所以不防设极小化序列全为非负函数序列.若
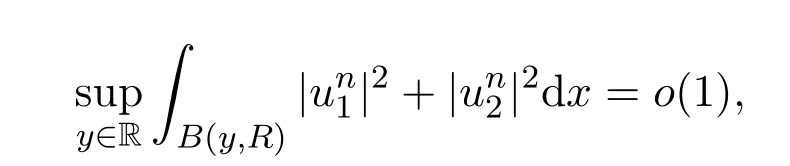
对一些R>0,则对任意2<p<6,i=1,2,在Lp(R)里有见文献[8]引理I.1.这与引理3.1(i)中m(a1,a2)<0相矛盾.因此,存在一个β0>0和一个序列{yn}⊂R,使得
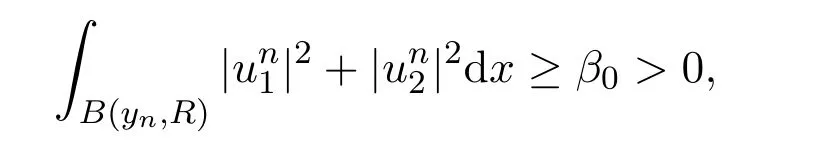
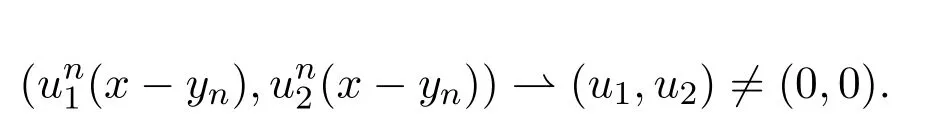
而该引理的主要目的是得到
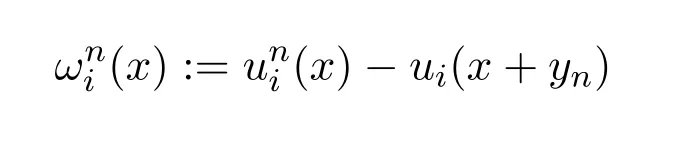
对所有的2<p<6,在Lp(R)中强收敛到0,i=1,2,为得到这个结论,利用反证法来证明,假设存在一个2<q<6,使得在Lq(R)×Lq(R)里在这些假设下,若

则再次利用文献[8]引理I.1,可以得出在Lp(R)里对所有的2<p<6,有
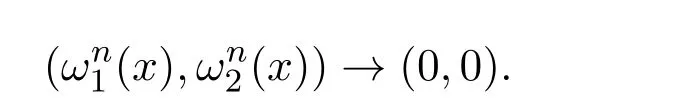
这与假设矛盾.因此,存在一个β1>0和一个序列{zn}⊂R,使得

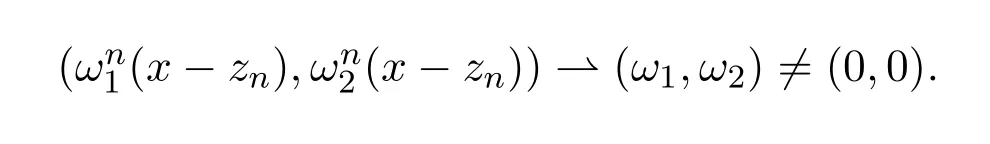
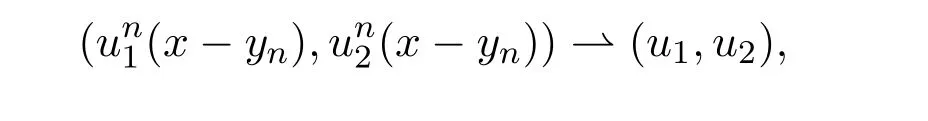
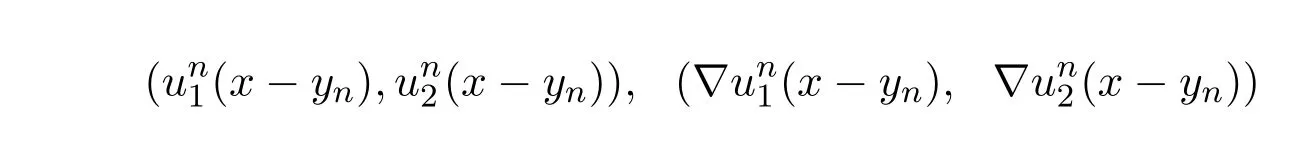
在 L2(R)×L2(R)里有界,且
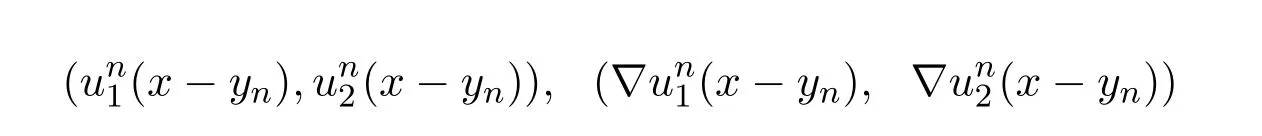
分别几乎处处收敛到(u1,u2)和(∇u1,∇u2),再由 (18)和(19)可知对所有
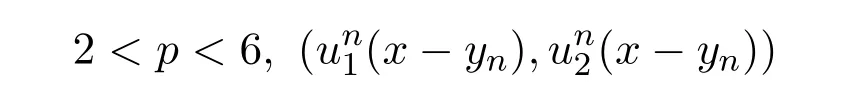
在Lp(R)×Lp(R)里是有界的,利用引理2.2,可得
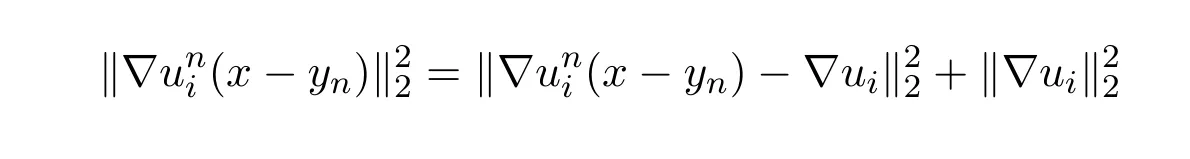
和
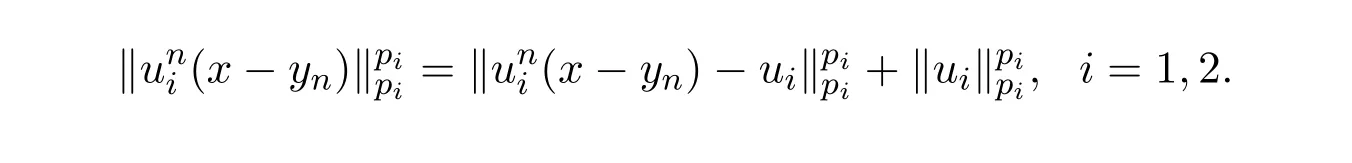
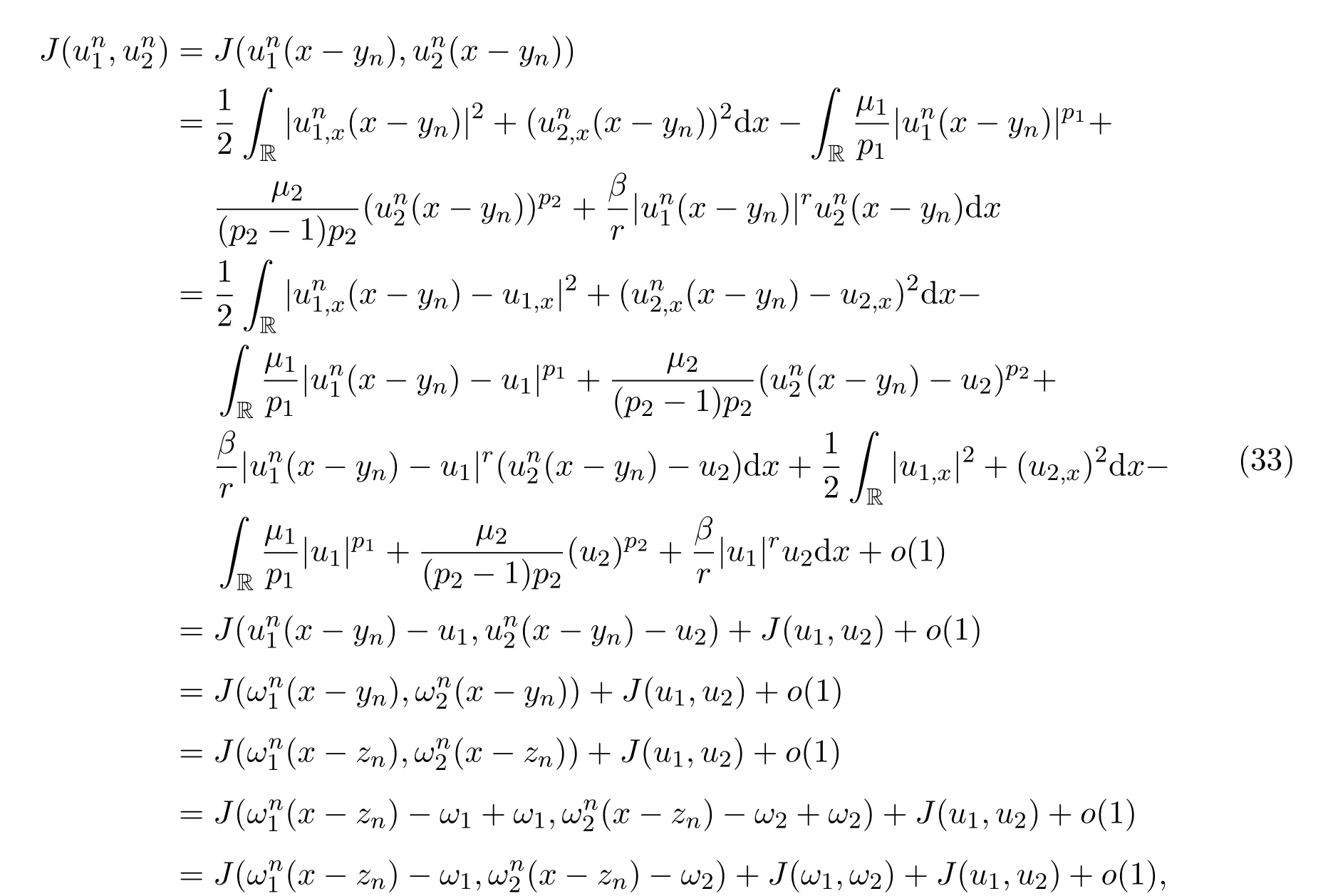


接下来的分情况讨论将利用到引理2.1,可以把所有的可能可归为以下两种情况.
利用引理2.1(ii),(iv)和(v),有
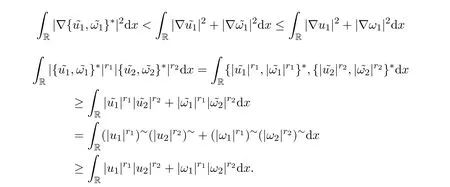
因此

再根据引理2.1(iii),对i=1,2,
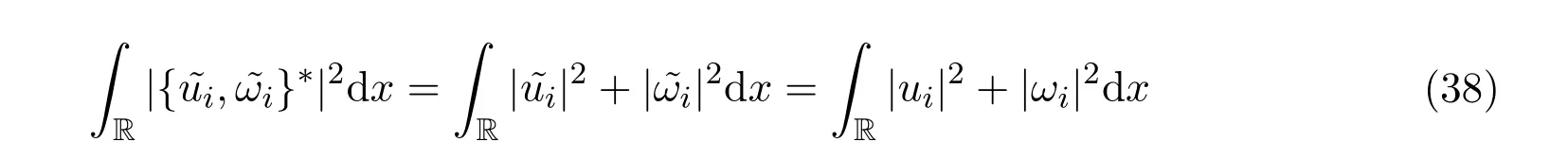
再利用公式3.10至公式3.12和引理3.1(iii),可得矛盾


和
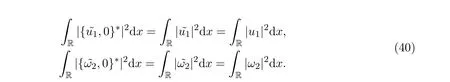
因此,利用公式3.10,公式3.13,公式3.15和引理3.1,同样可得

因此,对所有的2<p<6在Lp(R)里有

定理 1.1的证明令是泛函J在S(a1,a2)的极小化序列.由引理3.3,可知存在序列yn使得对2<p<6在Lp(R)里有
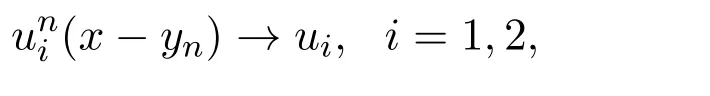
因此根据弱收敛

显然,若


假设

根据定义知J(u1,u2)≤m(b1,b2)和由3.15知
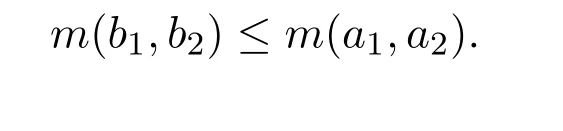
再根据引理3.1(iii)知,
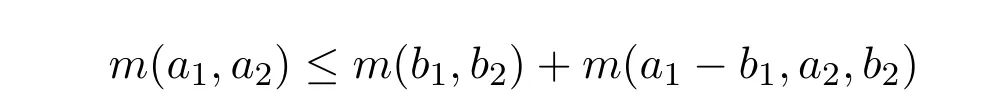
和引理3.1(i)知m(a1-b1,a2-b2)<0得到矛盾,因此定理1.1得证.
[1]Albert J,Bhattarai S.Existence and stability of a two-parameter family of solitary waves for an NLS-KdV system[J].Adv.Di ff erential Equations,2013,18:1129-1164.
[2]Albert J,Bona J,Saut J C.Model equations for waves in strati fi ed fl uids[J].Proc.Royal.Soc.of Edinburgh,Sect.A,1997,453:1233-1260.
[3]Funakoshi M,Oikawa M.The resonant interactions between a long internal gravity wave and a surface gravity wave packet[J].J.Phys.Soc.Japan,1983,52:1982-1995.
[4]Gou T,Jeanjean L.Existence and orbital stability of standing waves for nonlinear Schrdinger systems[J].Nonlinear Analysis:TMA,doi:10.1016/j.na.2016.05.016.
[5]Ikoma N.Compactness of minimizing sequences in nonlinear Schrdinger systems under multiconstraint conditions[J].Adv.Nonlinear Stud.,2014,14:115-136.
[6]Kawahara T,Sugimoto N,Kakutani T.Nonlinear interaction between short and long capillary-gravity waves[J].J.Phys.Soc.Japan,1975,35:1379-1386.
[7]Lieb E H,Loss M.Analysis[M].2nd ed.in:Graduate Studies in Mathematics,vol.14.American:Mathematical Society,Providence,2001.
[8]Lions P L.The concentration-compactness principle in the calculus of variations.The locally compact case,Part II[J].Ann.Inst.H.PoincarAnal.Non Lin´aire,1984,1:223-283.
[9]Miller P D.Applied Asymptotic Analysis[M].American:American Mathematical Soc.,2006.
[10]Newell A C.Solitons in Mathematics and Physics[M].Philadelphia:Society for Industrial and applied Mathematics,1985.
[11]Shibata M.A new rearrangement inequality and its application for L2-constraint minimizing problems[J].Mathematische Zeitschrift,2013(5):1-19.
[12]Whitham G.Linear and Nonlinear Waves[M].New York:Wiley,1974.
[13]宣本金.变分法:理论与应用[M].北京:中国科学技术出版社,2006.
Existence of solitary waves for coupled NLS-KdV system
Wu Ali,Wei Gongming
(University of Shanghai for Science and Technology,Shanghai200093,China)
In this paper,we study the existence of solitary waves for a NLS-KdV system. fi rst using the concentration-compactness principle to fi nd the precompactness of the minimizing sequences.then search the minimizers of functional for the system in H1(R)after a suitable translation.as a result the existence of nontrivial solution of original equations is proved.
NLS-KdV systems,solitary waves,minimizing sequences,symmetric-decreasing
O175.29
A
1008-5513(2017)04-0392-14
10.3969/j.issn.1008-5513.2017.04.007
2017-04-18.
国家自然科学基金(11471215);沪江基金(B14005).
吴阿丽(1992-),硕士生,研究方向:偏微分方程.
2010 MSC:34G20,47J30

