教学评估中的比较分析研究

马宁生

(同济大学物理科学与工程学院，上海 200092)

教学评估中的比较分析研究

马宁生

(同济大学物理科学与工程学院，上海 200092)

比较研究是教育技术中常用的一种方法，在用于教学研究中可获得教学的一般规律与特殊规律。本文简述了教学比较研究法的功能、作用和步骤。介绍了在实际教学中对不同对象和特质进行有效分析的几种案例。

教育技术；比较研究

比较是依据一定的标准，把彼此可能有某些联系的事物放在一起，寻找它们的异同，从而掌握研究对象的特征。教学比较研究是根据教学目标探究教学过程中存在的普遍规律与特殊规律的研究方法，从而探索教学规律。由于在比较研究中所研究的对象必须具备可比性，因而教学比较研究限定了研究的内容和范围，所以要准确把握研究对象的规定性。

1 教学比较研究法概述

1.1 教学比较研究法的功能[1]

教学比较研究可以帮助教学管理者和工作者把握教学过程中的一般规律，有助于深化教学理论的研究；探索教学规律和确定解决问题的策略，为教学实践提供依据。由于教学比较研究的特点在于其实践性和应用性，能使教学管理者和工作者更好地认识本地、本校和本班的教学状况，反思教学管理、教学方法和教学手段，为进一步提升教学管理和教学质量提供理论支持和数据依据，同时教学比较研究也是教学质量评价中的主要组成部分。

1.2 比较研究法的作用[2]

无论是比较研究采用何种形式，也无论是什么样的研究目标，我们都希望整个研究过程是有效的，也就是说我们所获得的数据是准确、可靠和客观的，所选择的研究方法已被证明是可行的，其结果能够进行明确的解释。在很多情况下，为比较研究所提供的数据是可重复的，也就是说在教学中的“实验”是可以重复和复制的。这样的比较研究才具有科学性，其成果才具有实用性和推广性，以达到对复杂事物认识其全面本质的作用。

1.3 运用比较研究法的步骤

比较研究法一般分4个步骤： (1)确定比较的问题，即选定比较的主题、确定比较的具体内容和划分比较的范围；(2)数据提取，即搜集资料并加以分类和编组；(3)选择比较的方法，即按照比较的目的选择相对应的一种或多种比较方法进行数据分析；(4)根据比较结果作进一步归纳和解释。

比较研究要从多个维度进行，同时要正确估计比较法的功能，同时与其他研究方法结合起来，形成比较完整、规范的比较研究体系。

2 教学比较研究案例

2.1 频数分布表的编制

下表的数据为某课程的学生成绩，绘制频数分布图。

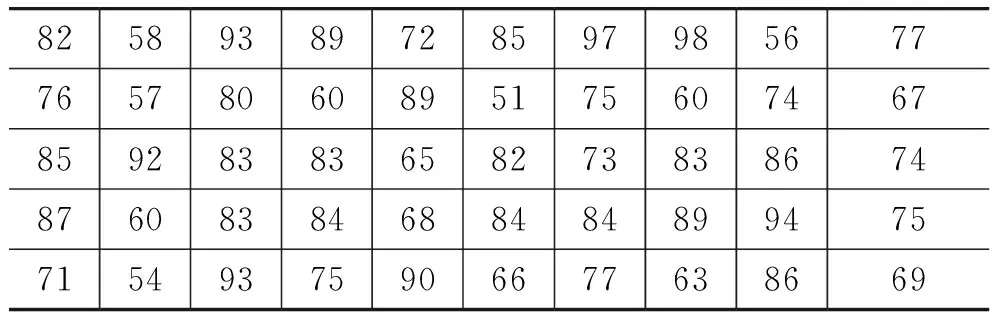
8258938972859798567776578060895175607467859283836582738386748760838468848489947571549375906677638669

根据以上数据，相关计算的数据列于下表。

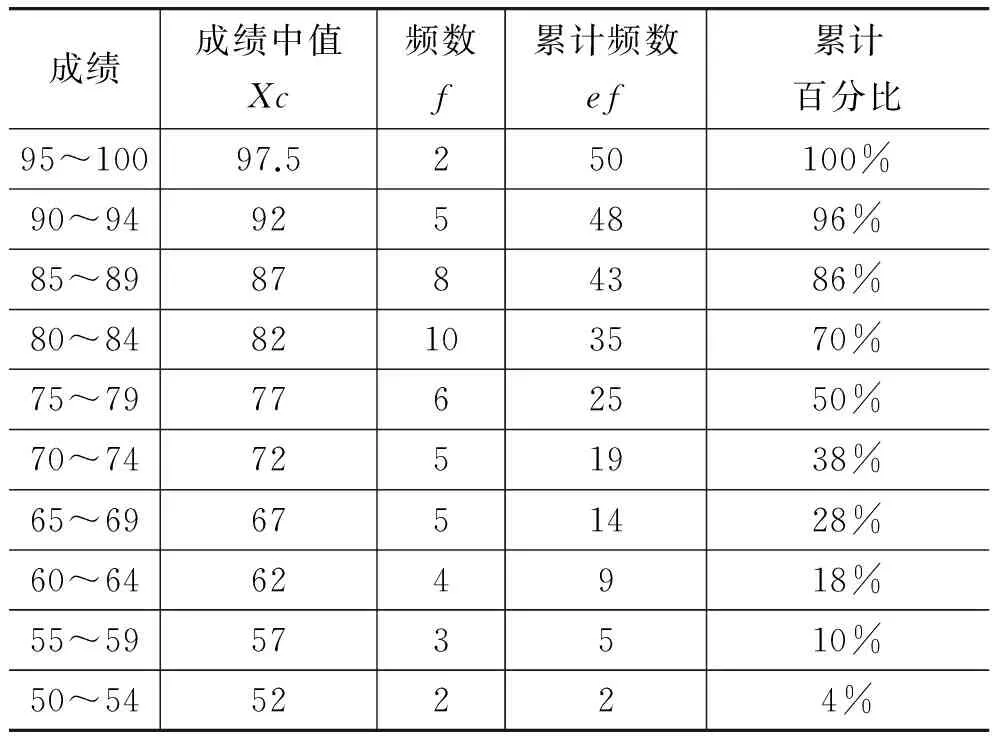
成绩成绩中值Xc频数f累计频数ef累计百分比95～10097.5250100%90～949254896%85～898784386%80～8482103570%75～797762550%70～747251938%65～696751428%60～64624918%55～59573510%50～5452224%

表中： 全距R=50(最大数-最小数)，组数k=10，区间i=5(i=R/k)，区间中值Xc=(每组的最低值+每组最高值)/2，f为区间内的频数。

1) 频数分布直方图

在直角坐标系中，区间由直杆的宽度表示，频数由直杆的高度表示。该图表可直观反映学生成绩的分布情况，连续、非连续数据均可用使用(见图1)。

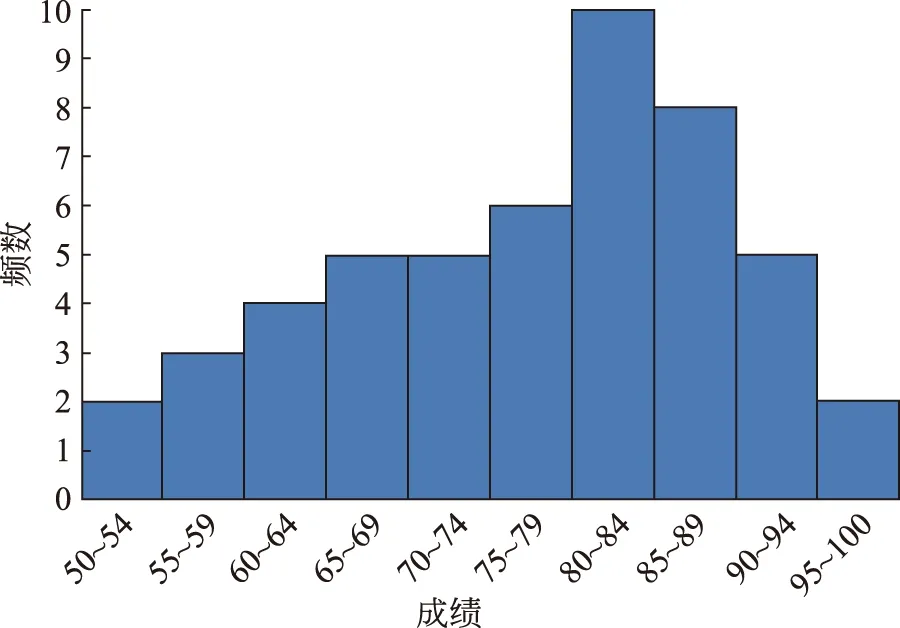
图1 频数分布直方图

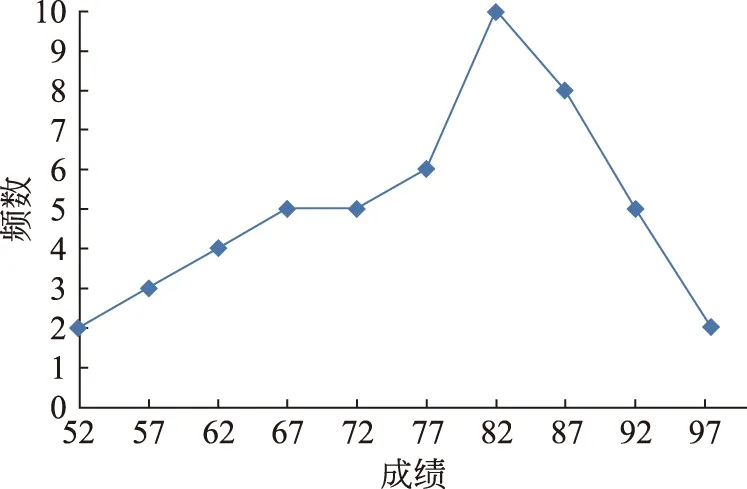
图2 频数分布曲线图

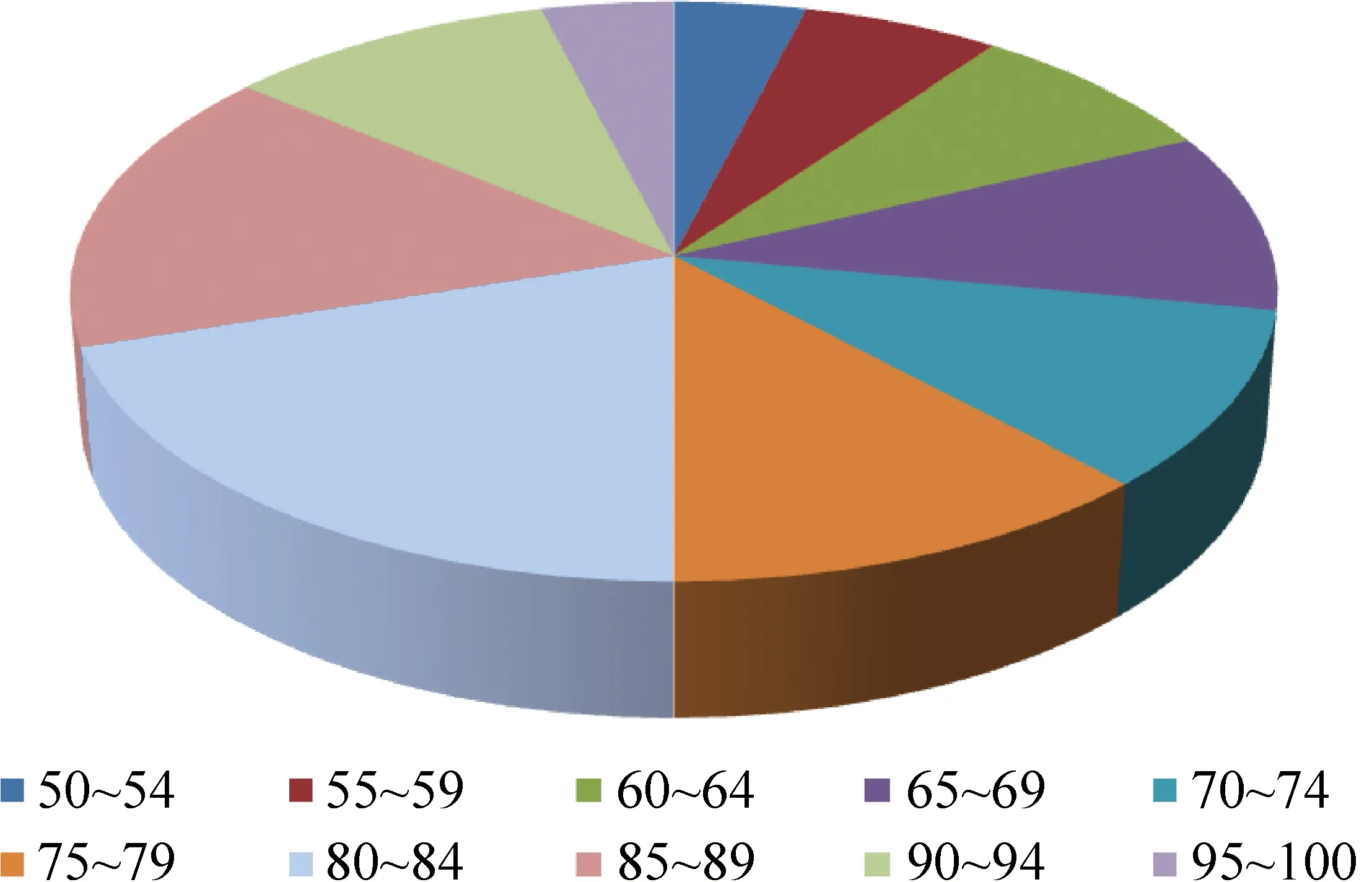
图3 频数分布圆形图

2) 频数分布曲线图

根据频数分布表，用一条封闭多边形折线显示连续数据的分布情况，同样可反映学生成绩的分布情况(见图2)。

3) 频数分布圆形图(扇形图)

以圆形表示全部频数，以扇形面积表示每一组的频数百分比，它能直观反映出各成绩的占比情况(见图3)。

4) 积累频数曲线(S曲线即百分位等级曲线)

累积频率曲线是根据频数分布表，显示数据的频数的变化积累，形成S曲线。通过使用S曲线，可以确定一个分数在整个序列中的位置——百分位等级(参见图4)。

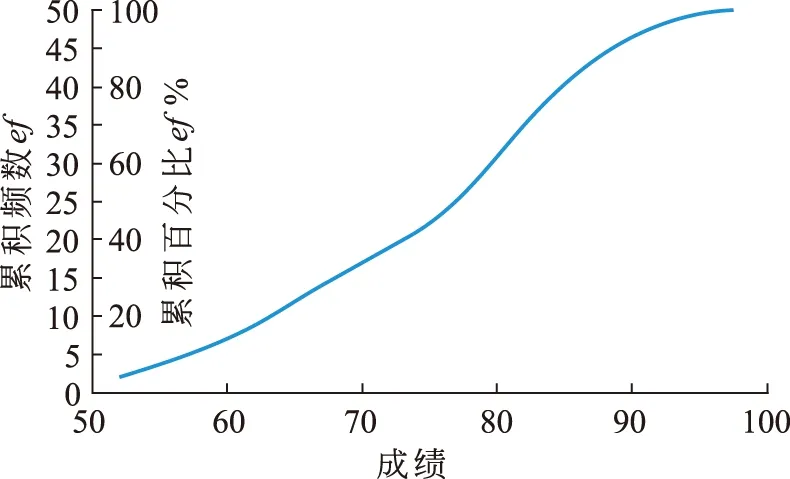
图4 积累频数曲线

百分位等级的计算公式为：

其中，PR是百分位等级，f是该分数区间内的频数，X为分数，L是区间的下限，i为组距，Fb是小于L的向上积累数，N是总数。通过计算PR，可以确定不同等级在百分位等级中的位置，例如86分在百分位等级中的位置是PR=[10×(86-85)/5+35]×100/50=74分。

2.2 相关关系的度量

关联性是指事物、现象之间的某种关系的存在。存在相关，但不一定是因果关系。相关度用r表示，下表是r的值和相关度。

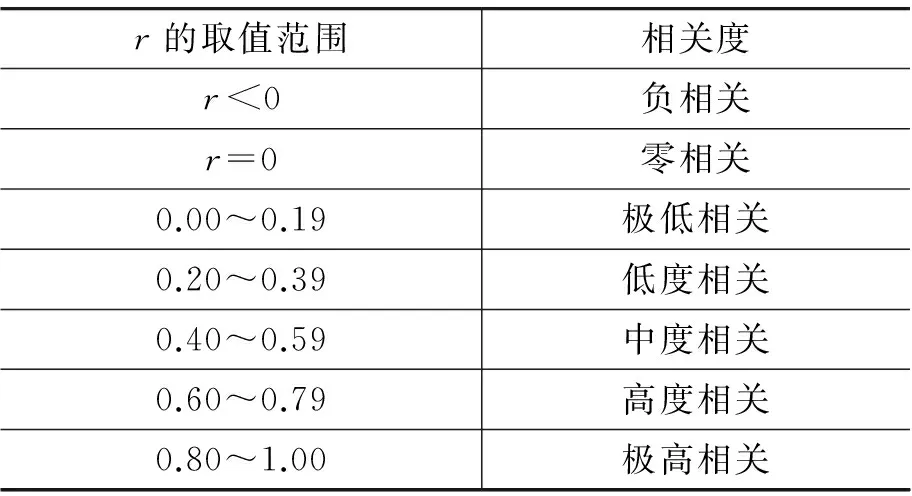
r的取值范围相关度r<0负相关r=0零相关0.00～0.19极低相关0.20～0.39低度相关0.40～0.59中度相关0.60～0.79高度相关0.80～1.00极高相关

例如，有14名学生参加了大学语文和高等数学竞赛，其成绩如下表所示。

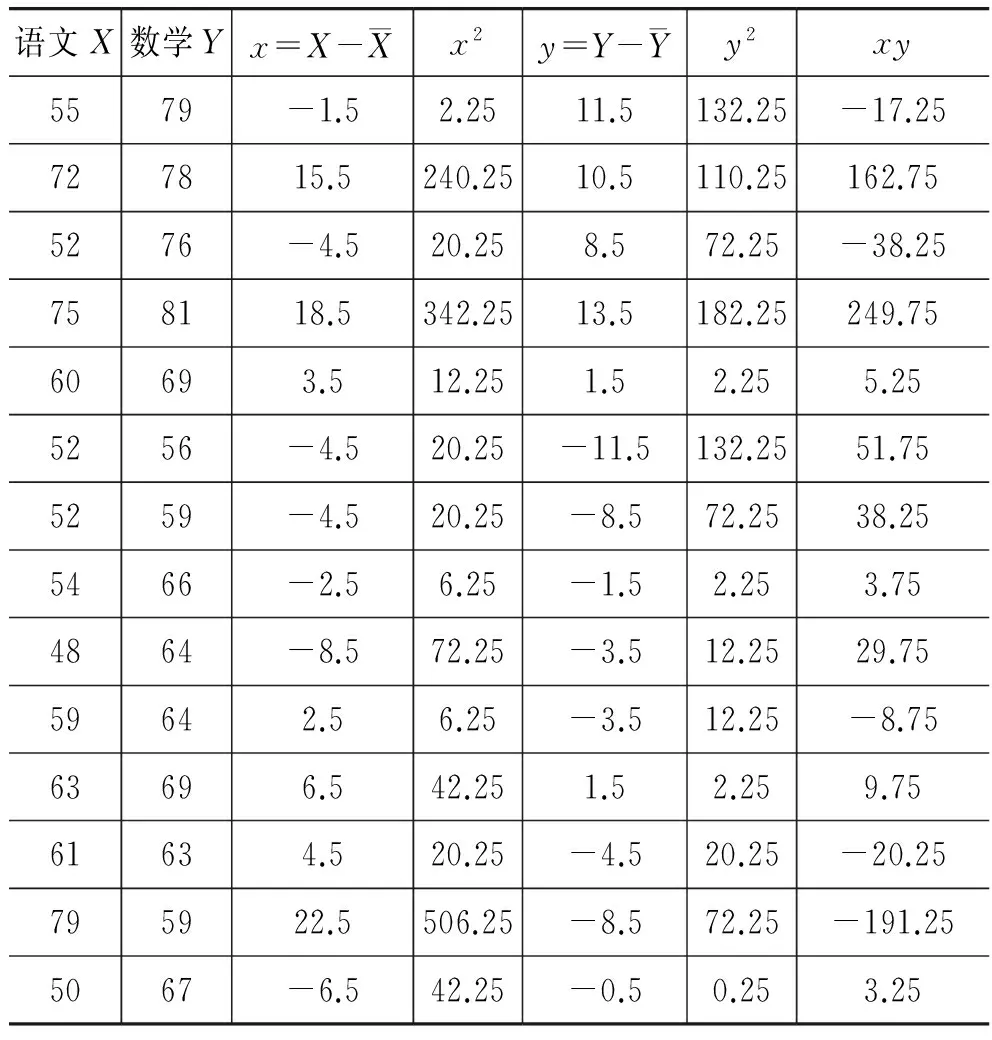
语文X数学Yx=X-Xx2y=Y-Yy2xy5579-1.52.2511.5132.25-17.25727815.5240.2510.5110.25162.755276-4.520.258.572.25-38.25758118.5342.2513.5182.25249.7560693.512.251.52.255.255256-4.520.25-11.5132.2551.755259-4.520.25-8.572.2538.255466-2.56.25-1.52.253.754864-8.572.25-3.512.2529.7559642.56.25-3.512.25-8.7563696.542.251.52.259.7561634.520.25-4.520.25-20.25795922.5506.25-8.572.25-191.255067-6.542.25-0.50.253.25

计算公式为：

语文成绩的标准差为SX=9.83，数学成绩的标准差为SY= 7.68，计算得到r=0.263，说明以上两门课程的成绩是不相关的。

2.3 等级相关

等级相关是指当两个变量之间以等级次序排列时，这两个变量之间的相关程度，它是不连续变量的等级成对数据，组内各数据相互独立，其特点是不够精确，但应用面较广。主要包括斯皮尔曼(Spearman)二列等级相关和肯德尔(Kandall)多列等级相关。

(1) 斯皮尔曼(C.Spearman)相关——等级相关系数

计算公式为：

其中Rs为斯皮尔曼相关系数，D为X与Y成对变量等级之差(Rx-Ry)，N为变量的个数。例如某校8名学生的大学物理和物理实验的考试成绩如下表所示。

大学物理X7860858675906870物理实验Y8269728274897663

通过上述公式计算得到Rs=0.696，说明上述两门课程的成绩存在高度相关性。

(2) 肯德尔等级相关——肯德尔和谐系数(评分者等级相关系数)

表示几个评定者对同一组对象中的内容进行评级后所获得的一致性程度。计算公式为

其中R为每个对象的等级总和，N是被评估对象的数目，K是评价者的人数。例如某校的六位督导员对该校中的7个班级进行教学检查，评价等级如表所示。

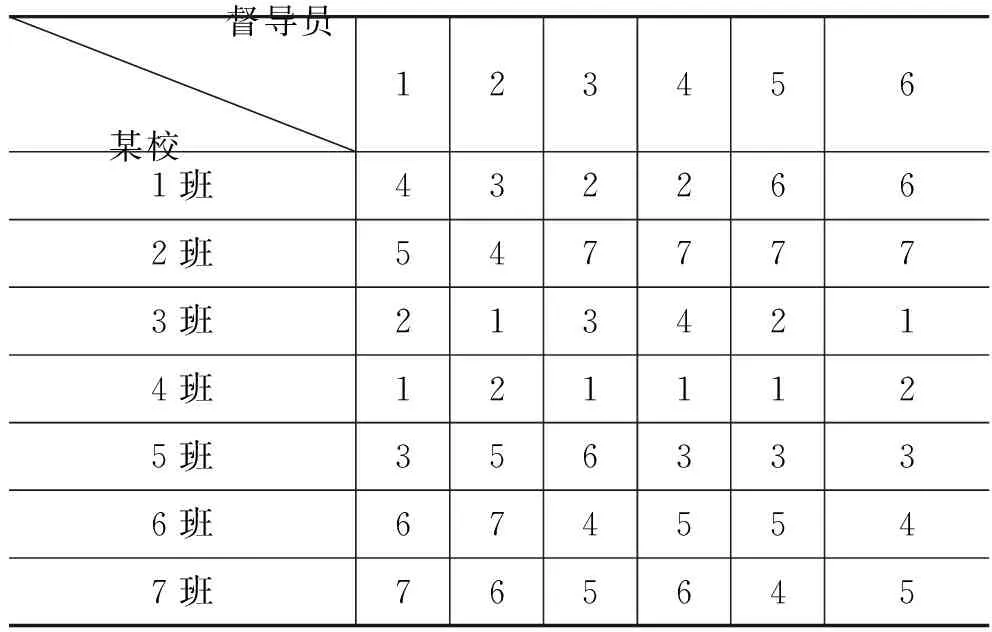
督导员某校 1234561班4322662班5477773班2134214班1211125班3563336班6745547班765645

得知N=7，K=6，计算得到W=0.673，说明他们意见有高度的一致性。这种多列等级相关也可以应用到专家评审系统中对多序列项目的综合评审和考核，同样在教学比较研究中可作为对象选拔的方法之一。

2.4 点二列相关

根据对象的特质，将变量分为两列x和y序列，并检验这两个变量之间的相关性。在教学比较研究中主要用来评价考试内容的一致性、鉴定题目的区分度及考试成绩与考试总分之间是否一致的问题。用点二列相关分析法是分析试题质量的重要方法之一。

计算公式为：

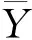
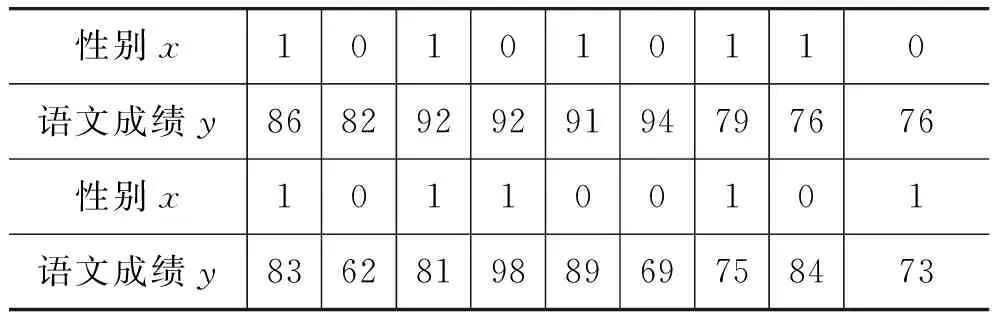
性别x101010110语文成绩y868292929194797676性别x101100101语文成绩y836281988969758473

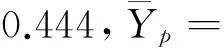
2.5 标准分数(Z分数)

标准分数，又叫Z分数，是以标准差为单位表示一个数据在团体中的相对位置。在教学比较研究中一般用于同科多次考试成绩之间的对比、不同科考试成绩之间的对比和多科成绩之间的对比。标准分数的计算公式为：

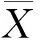
2.6 单样本的双侧t检验

进行样本均数与已知总体均数的比较，其目的是推断样本所代表的未知总体均数与已知的总体均数有无差别。

例如某校大学生期中物理考试的平均分数为72.3分，标准差为15分，期末考试后，随机抽取21人的物理成绩，其平均分数为80.1分。试问学生的物理成绩有没有显著提高？

自由度为df=n-1=20，查t界值表，t(20)0.05=2.086，由于t>t(20)0.05，按P=0.05水准判断，学生的物理成绩有明显进步。

在教学的实践过程中，采用了某种新的教学方法(例如翻转课堂教学、提问式教学等)，如果我们暂不考虑过程评价中学生感知的量化测评数据，仅仅通过学生的成绩来评估这一教学方法的效果，用单样本的双侧t检验是一种即实用又便捷的评估方法。例如某课程的测验平均成绩为74.1分，标准差为6.9分，教师采用了一种新的教学方法后再进行一次课程测验。对25名学生进行随机抽样调查，平均得分为77.8分。通过以上计算，t=2.627>t(24)0.05=2.064，按P=0.05水准判断，该课程学生的成绩有明显提高，说明所采取的这种教学方法对提高学生的成绩是有帮助的，值得推广。

3 结语

采用比较研究的方法，可以对学生的学习成绩进行快速准确的分析，使教育工作者尤其是一线教师了解学生的学习状况，通过比较不同课程和不同班级学生成绩的差异并结合学生问卷调查和专家评审的定量数据处理，为教学方法和教学手段实施的有效性提供了一种便捷的检验方法。

[1] 袁振国.教育研究方法[M].北京：高等教育出版社，2000.

[2] 谢幼如,李克东.教育技术学研究方法基础[M].北京：高等教育出版社，2006.

■

RESEARCH ON THE COMPARATIVE ANALYSIS OF TEACHING ASSESSMENT

Ma Ningsheng

(School of Physics Science and Engineering, Tongji University, Shanghai 200092)

Comparative study is a kind of method that is commonly used in education technology, it can be obtained general and special regular in the study of education. This paper briefly describes the function, the role and methods of comparative research. In this paper introduced several comparative analysis of the case that can carry on the effective analysis to the different objects and qualities in the practical teaching.

education technology; comparative analysis

2017-07-04

上海市哲学社会科学规划教育学一般项目(项目批准号A1610)；2017年度同济大学研究生教育改革与研究项目。

马宁生，男，副教授，从事物理教学和教育技术研究，maningsheng2005@163.com。

马宁生. 教学评估中的比较分析研究[J]. 物理与工程，2017，27(5)：95-98.