正则动量面面观
徐 湛
(清华大学物理系,北京 100084)
教学研究
正则动量面面观
徐 湛
(清华大学物理系,北京 100084)
对于带电粒子在磁场中的运动,一个很重要的概念是粒子的正则动量不同于它的机械动量,而这一点经常被忽视或者被混淆。本文从正则动量的基本定义出发,从经典的和量子的两方面分析了正则动量和机械动量的关系,指出正则动量才是基本的动力学变量。最后以磁镜装置为例说明了如何应用正则动量简明地给出问题的答案。
磁场;矢量势;正则动量;规范变换;磁镜装置
1 经典力学: 带电粒子在磁场中的3种动量
对于带电粒子在磁场中的运动,首先想到的当然是它的运动方程。假设粒子的质量是m,电荷是q,空间中的稳恒磁场是B(r),那么熟知它的运动方程是
(1)
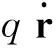
(2)
其中A(r)是磁场B(r)的矢量势[2],它的旋度给出了磁场
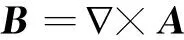
(3)
通常还假设它满足规范条件(橫场条件)

(4)
证明如下。现在欧拉方程是
其中i,j=1,2,3(=x,y,z)并且对j求和。在此式中取i=1,那么
对于i=2,3也类似,这表明欧拉方程是
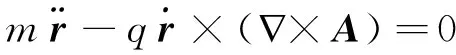
再注意到式(3),它正是方程(1)。现在问题来了:这时的正则动量p是什么?按照分析力学的正则动量的定义[1],它是
(5)
再过渡到分析力学的哈密顿形式(亦称正则形式),系统的哈密顿量是拉格朗日量的勒让德变换,即
(6)
注意: 哈密顿量要以正则坐标和正则动量为独立自变量。用这个哈密顿量写出的正则运动方程
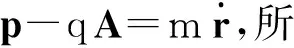
从正则运动方程很容易看出系统的对称性与守恒量之间的关系:如果哈密顿量和某个正则坐标qi无关(这样的坐标被称为循环坐标),那么与qi共轭的正则动量pi就是守恒量,因为
这里必须避免两个误解。第一个是把系统的对称性认为是磁场的对称性(比如磁场在平移、旋转等等操作下不变),但事实上哈密顿量里出现的不是磁场而是矢量势,所以系统的对称性指的是矢量势的对称性,不是磁场的对称性。第二个是把守恒量当成机械动量,但事实上守恒的是正则动量,它在机械动量之外还要再加上电磁动量。实践表明,这两个误解经常出现,有时候连学过高等物理的人也难以避免。
最后一个问题是规范变换不变性。熟知若矢量势A受到规范变换
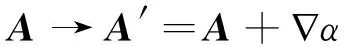
(7)
其中α是任意函数,那么磁场B并不改变:

(8)
所以运动方程也不改变。从拉格朗日量的角度说,在A的规范变换下它增加了一项对时间的全导数项,与原来的拉格朗日量虽然不相等但却是等价的,而从哈密顿量的角度说,它在A的规范变换下完全不变。这就是理论的规范变换不变性。但是必须注意,这时正则动量是要变的,因为它的变换是
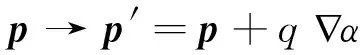
(9)
也就是说正则动量并不是规范不变量,所以它不是可观察量。这使我们处在一个微妙的境地:当粒子在磁场中运动时,机械动量是我们实际观察的,而正则动量虽然是基本的动力学变量却不是可观察的。这是理解正则动量概念的困难所在。
2 带电粒子在匀强磁场中的平面运动
现在考虑一个最简单的例子。设沿着+z轴方向有一个匀强磁场
(10)
而带电粒子被限制在xy平面内运动。熟知这时粒子的运动是匀速圆周运动(同步回旋运动)。假设圆的半径是R,粒子运动的角速度(圆频率)是ωc,那么运动方程就是
所以
(11)
也就是说,ωc只取决于粒子的荷质比|q|/m和磁场强度B,这个频率称为同步回旋频率。当然,粒子运动轨道的半径R、圆心位置C和运动速度v是由初始条件决定的。至于粒子在轨道上的转动方向,用矢量叉积的右手螺旋法则不难定出:从xy平面的上方向下看,q>0时粒子顺时针旋转,q<0时逆时针旋转。
为了更深入地理解这个运动,让我们看看粒子的3种动量。首先要为磁场B选择一个矢量势。不难证明可选
(12)
这是因为
而且
这称为矢量势的对称规范。因而哈密顿量成为
(13)
这个哈密顿量显然是绕z轴旋转(也就是在xy平面上绕原点旋转)不变的,所以粒子角动量的z分量是守恒的。问题是哪个角动量?是机械角动量吗?不是。应该是正则角动量。注意,粒子运动轨道的圆心可能在平面上的任何一点,而如果圆心不在原点,它的机械角动量的z分量显然不是常数。下面我们来证明:无论粒子的运动轨道的圆心在哪一点,粒子的正则角动量的z分量是守恒的。为确定起见,假设粒子就是电子即q=-e(e>0),因而是逆时针旋转的,轨道的圆心在rc,半径是R,那么根据前面的分析,电子的运动是
x(t)=xc+Rcosωct,
y(t)=yc+Rsinωct
所以机械动量的分量是
电磁动量的分量是
因而正则动量的分量是
由此可知正则角动量的z分量是
它的确是常数。此外还有一件有趣的事情:按照通常的理解,当粒子做逆时针转动时,它的角动量的z分量是大于零的,但是现在我们发现:如果rc>R,lz是小于零的。其原因在于:粒子的机械角动量的平均值总是大于零的,并且与rc的位置无关,但电磁角动量的平均值总是小于零的,并且随着rc离开原点而变得越来越大,到后来就会压过机械角动量而成为正则角动量的主要成分。这向我们提示了正则动量和机械动量有重要区别,在某些条件下,它们甚至可能有完全相反的特征。
前面还提到:正则动量依赖于规范的选择。所以,“正则角动量的z分量守恒”这个结论,其实只在对称规范下才成立,如果换一个规范的话,守恒量就是别的量了。比如我们重新选择所谓的朗道规范

(14)
(15)
显然,这个哈密顿量不再具有旋转不变性,而是变为具有x方向的平移不变性(哈密顿量与坐标x无关),因而正则动量(不是机械动量)的x分量是守恒的。验证如下。粒子的运动仍然如前,所以它的机械动量还是一样,然而电磁动量变为
-eAx(t)=eByc+eBRsinωct
因而正则动量的x分量是
eByc+eBRsinωct=eByc
它的确是常数。在粒子的圆周运动中却存在着守恒的线动量,不能不说是非常新奇的事,而这也来自于正则动量不同于机械动量。
通常来说人们习惯的认识是:确定的运动有确定的守恒量。然而这个例子告诉我们:对于磁场中的带电粒子,尽管粒子的运动是完全确定的,守恒量却会随着规范势的不同选择而改变。这使我们运用守恒定律时必须特别小心。
3 量子力学: 正则动量算符和几率流


(16)
所以哈密顿量也变成了算符(仍然是对电子)
(17)
如果矢量势A满足规范条件(4),则哈密顿量算符也可以写成
(18)
问题是: 在经典力学里,我们是通过机械动量和电磁动量来理解正则动量,而量子力学的情况却倒过来了:我们的出发点就是正则动量,那么机械动量体现在哪里?为了回答这个问题,我们先写下相应的薛定谔方程:
(19)
其中Ψ(r,t)是波函数,所以
取复共轭得
根据玻恩对波函数的几率解释,ρ=|Ψ|2=Ψ*Ψ是坐标几率密度,从以上两式可得ρ对时间的变化率为
若记
j=
(20)
就有方程
(21)
这表达了几率守恒,其中j应理解为坐标几率流密度。众所周知,在电荷守恒的情况下,如果空间电荷密度是ρ,电荷平均速度是,那么电流密度就是j=ρ。把这里的情况与之对照,可以把式(20)重写为
(22)

(23)
对于前面所举的例子即电子在匀强磁场中的运动,在对称规范的情形下,哈密顿量算符是
(24)
不难发现
(25)
(26)

(27)
其中ωc=e B/m就是同步回旋频率,但是这些能级是无穷度简并的(对于无限大平面),比如对于基态(n=0),就有无穷多个波函数
(28)

对称规范的矢量势在xy平面内也可以写为
所以对于式(28)的波函数,(22)式的坐标几率流密度j的正则动量部分是
由于M≤0,所以它是逆着eφ方向的,而电磁动量部分是
它是顺着eφ方向的,二者之和是
尽管M≤0,足够大的u总可以使u2+M >0,即粒子的几率流顺着eφ的方向。这和粒子的经典运动图像是一致的。
如果取朗道规范,那么哈密顿量算符是
(29)
这时
(30)

(31)

(32)
这正是在y轴上固有频率为ωc的线性谐振子的薛定谔方程,只不过势能曲线的对称轴是y=y0,所以我们仍然得到式(27)给出的能谱,但能级的简并变成了不同的px值。现在基态(n=0)的波函数变为
(33)
(C′是归一化因子),因而几率流密度j的正则动量部分只有x分量,其值为
j的电磁动量部分也只有x分量,其值为
二者相加给出
当y>y0时jx<0,粒子的坐标几率流朝左,而y
4 量子力学理论的规范不变性
在量子力学里,正则动量的算符表示总是-i,与矢量势的选择无关,但我们不能因此就说量子力学里的正则动量是规范不变量。事实上,在量子力学里,物理量的测量结果不仅仅与代表它的算符有关,而且和波函数也有关。所以我们还要问:在规范变换下,波函数怎么变?可以证明,为了保证理论的规范不变性,当规范势受到变换A→A′=A+α的时候,波函数要受到变换
(34)

(35)
对这个方程进行规范变换,即是把其中的Ψ和A换成Ψ′和A′,则左方变为
右方变为
因此仍然有
(36)
即是薛定谔方程在规范变换下不变,所以量子力学理论是规范不变的理论。
5 关于磁镜装置的讨论
磁镜是利用磁场对等离子体的运动进行约束的装置[3],图1(取自文献[3])是一种比较典型的磁镜。两个同样的通电圆线圈同轴地放置,因而产生了两头强中间弱的磁场,这种磁场就可以把在其中运动的离子在强磁场处反射回去,如同镜子反射光线一样,所以被称为磁镜。利用正则动量的概念,我们对它的工作原理分析如下。
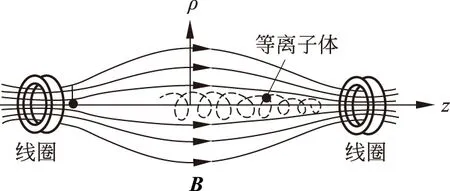
图1 磁镜装置示意图
由图1可知在磁镜装置的轴线(z轴)附近,采用柱坐标系(ρ,φ,z),磁场B是
(37)
由此可知
因而磁场的分布是
(38)
其中B(z)(>0)是已知函数(文献[3]中有式(37)但并未给出式(38))。那么什么样的A可以给出这样的B?利用柱坐标系中的旋度公式
不难证明可以取
(39)
由于这个A与时间t无关,也与角度φ无关,所以离子的动能和它的正则角动量的z轴分量都是守恒的,即有
(40)
和
(41)
其中离子的运动由ρ(t),φ(t),z(t)描写,vρ≡dρ/dt,vφ≡ρ(dφ/dt),vz≡dz/dt,离子的电荷q>0。在分析力学中,这样的守恒方程被称为运动方程的一次积分。其实,即便不引入正则动量的概念,式(41)也可以藉运动方程m(d/dt)=q×B的柱坐标形式
(42)
(43)
(44)
直接导出(文献[3]没有引入矢量势A,也没有写出完整的离子运动方程,因而没能给出式(41))。由于离子在磁场中的回旋运动非常之快,当它完成一周的回旋运动时在z方向上只移动了很小的距离,所以我们可以对它应用绝热近似,即假设离子的回旋频率(参见式(11))完全由当地的磁场所决定,这样就有
(45)
把它代入式(42)中,就得到
(46)
由此可知vρ=常数。但文献[3]的式(2)未说明理由就取了vρ=0,未免过于武断。实际上,从图1也可以看出vρ是不等于零的。与此同时,两个一次积分也分别变为
(47)
(48)

(49)

(50)
的时候,离子运动到那一点就有vz=0,因而不再向前运动了。这就是磁镜装置的基本工作原理。式(50)和文献[3]的最后结果(即它的式(10))是一致的,但这里的分析更严格,补充了一些它没给的式子,还指出了它的某些式子实际上是错的。
[1] 周衍柏. 理论力学教程[M]. 3版. 北京,高等教育出版社,2009.
[2] 郭硕鸿. 电动力学[M]. 3版. 北京,高等教育出版社,2008.
[3] 张琳,蔡莉莉. 磁镜原理及其在磁约束中的应用[J]. 物理与工程,2013,23(3): 16-18.ZhangLin,CaiLili.Principleofmagneticmirroranditsapplicationinmagneticconfinement[J].PhysicsandEngineering, 2013, 23(3): 16-18. (inChinese)
■
MANY FACES OF CANONICAL MOMENTUM
For movement of a charged particle in a magnetic field, a very important concept is that the canonical momentum of the particle is different from its mechanical momentum, which is often overlooked or confused. Based on the fundamental definition of canonical momentum, this paper analyzes the relationship between canonical momentum and mechanical momentum from classical and quantum aspects, and emphasizes that the basic dynamic variable is the canonical momentum. Finally, as an example, the magnetic mirror device is studied to illustrate how the canonical momentum concisely gives the answer to a problem.
magnetic field; vector potential; canonical momentum; gauge transformation; magnetic mirror device
2017-05-26
徐湛,男,教授,主要从事物理科研和教学工作,研究方向为理论物理,zx-dmp@tsinghua.edu.cn。
徐湛. 正则动量面面观[J]. 物理与工程,2017,27(5):3-9.
Xu Zhan
(Department of Physics, Tsinghua University, Beijing 100084)

