大顶角等腰劈的等倾干涉原理
周国全 祁 宁
(武汉大学物理科学与技术学院,湖北 武汉 430072)
大顶角等腰劈的等倾干涉原理
周国全 祁 宁
(武汉大学物理科学与技术学院,湖北 武汉 430072)
依据波动光学关于光的干涉原理, 分析和介绍了一种能产生等倾干涉现象的大顶角等腰劈干涉装置,推导并讨论了该干涉结构发生等倾干涉的条件及干涉条纹的分布规律;同时指明等腰劈的等倾干涉原理对于薄膜干涉的相似性或等价性,并讨论了其在光学领域可能的应用领域;强调了其对光学干涉的教学研究的辅助作用及内容扩充。
光学干涉; 等倾干涉;干涉圆环;等腰劈;光学谐振腔, 微位移传感
两列(或多列)光波相遇而发生干涉需要满足三个条件[1-3]:(1)频率相同;(2)振动方向相同;(3)相位差(或初相位差)恒定。这种能够发生干涉现象的两列(或多列)波称为相干波(coherent waves)。不同的光学干涉装置就是用不同的方式满足以上(尤其是第三个)干涉条件[1-9]。按照参与干涉的光束个数分为两大类:双光束干涉与多光束干涉;按照产生相干光束的方式则分为波前分割与振幅分割式;而按照干涉的光程差函数与场强函数的等值变量来分类,则分为等厚干涉与等倾干涉,例如法布里——伯罗(F-P)干涉仪和迈克尔逊干涉仪。文献[4]论述了两种振幅分割式多光束等倾干涉结构――矩形腔与大顶角等腰劈干涉结构,并初步验证了其干涉理论;文献[5-9]论述了若干等厚干涉结构及其干涉理论。通常等倾干涉是指扩展光源照射在厚度相等的薄膜上产生的干涉现象,具有不同倾角的入射光各自干涉,形成对应的不同干涉条纹,同一级条纹对应着同一倾角,不同级条纹对应着不同的倾角。薄膜上下两表面对同一条入射光的反射光线是相互平行的,两反射光线在无限远处相遇并产生非定域干涉条纹,即定域在无穷远处或观测透镜的焦平面上。
有关光波在三棱柱腔内外横向传播的规律的研究,鲜见于波导型光学谐振腔的文献中。本文详尽深入地分析了文献[4]已初步论述的大顶角等腰劈等倾干涉结构。研究表明,光波在等腰劈内外的横向传播将发生振幅分割式多光束等倾干涉现象。本文和文献[10]这两种干涉结构不仅对于F-P干涉技术具有等效性、替代性与补充作用,而且还具有若干新的特点和应用前景[11-14]。
1 等腰劈的等倾干涉原理
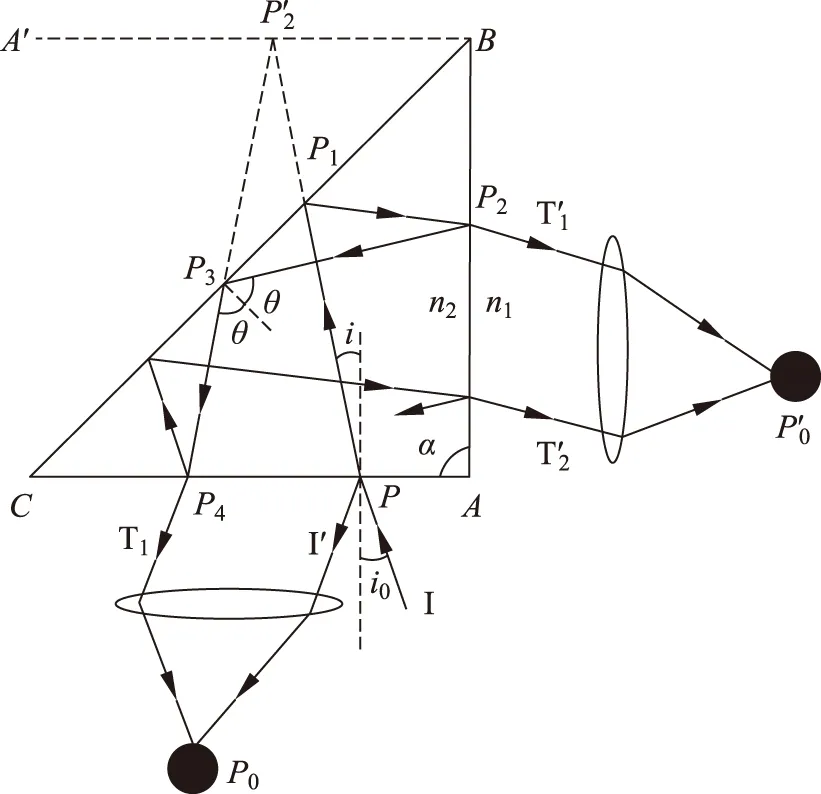
图1 等腰劈等倾干涉装置结构图
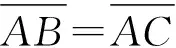

Δ=2n2hcosi
(1)
其相应的表观相位差为
(2)
其中h为△ABC在腰AC上的高线长,λ为入射光在真空中波长,腔内折射角i满足折射定律n2sini=n1sini0, 由于光程差与入射点P位置无关并恒定,相邻的两次反射线之间满足干涉条件。下面我们将推导反射线光束(或透射线光束)的干涉条纹的亮暗条件,并推导干涉场光强的分布函数。
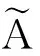
(3)
将反射线集合的振幅相加可得
(4)
其中用到了斯托克斯公式r2+tt′=1;r′=-r。r2=r′2=R为反射系数。尤请注意:由于每束光线在棱镜的“底边”BC表面来回反射两次,两次半波损失等效于没有位相突变。推导过程中也不需要重复(额外)计入其他反射点可能存在的半波损失及位相突变,它们均已体现在Stokes 关系式r′=-r的负号中——界面两侧反射时会有π的位相差异。另一方面,反射光干涉光强分布公式为
(5)
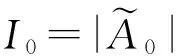
(6)
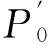
(7)
时,透射光干涉场强式(6)极大;相应的反射光干涉场强式(5)极小。当折射角i满足cosδ=-1, 即
(8)
时,透射光干涉场强式(6)极小;反射光干涉场强式(5)极大。由式(1)、(2)、(5)、(8)可知,显然这里发生的是等倾干涉,因为干涉场的光强分布及光程、相位差公式(1)、(2)、(5)、(8)随入射角i0而变,同一极大环纹对应于同一入射角(或折射角)。

图2 等腰劈等倾干涉实验条纹
初步的实验和我们进一步的实验都表明,这种等腰劈干涉装置能够实现多光束等倾干涉——当使用扩展光源照明时,无论是反射线集合,还是透射线集合,都能借助凸透镜与观测屏观察到非定域的等倾干涉圆环。如图2所示的干涉图像是等腰直角劈产生的透射光等倾干涉条纹。实验中使用了波长为632.8nm的He-Ne激光单色光源,其高斯型激光束经扩束镜后形成的发散光束(而不是扩展光源)作为入射光束进入干涉装置。实验中最多约观察到8个较清晰的干涉圆环。既然等腰劈干涉装置等效于平行薄膜的等倾干涉,显然其干涉圆环形条纹的分布规律亦与其相同,内疏外密,不等间隔分布,中央斑点具有最高干涉级序;其干涉场强的半值宽度的公式也与之相同。另外可以证明,相邻两亮(或暗)纹的半径之平方差是与干涉序无关的常量。如图3所示,观测屏e在透镜d的后焦面处,设干涉圆环的圆心处斑点正好是第m级干涉极大(对应的折射角为θ0=0),其干涉序m最大(因其对应的光程差最大);对于在A′B处以小角度θk折射的光线,设它们在屏上的干涉场点P落在第m-k级干涉极大圆环上(即第k个极大圆环条纹上),则在如图所示的直角三角形中,小角θk≈tanθk≈rk/f=Dk/2f;运用余弦展开的泰勒公式,忽略高阶无穷小项,可得
(9)
(10)
同理对第m-(k+1)级干涉圆环,(第k+1个圆环)可得,
图3 干涉条纹分布规律的推导
联立(9-12)诸式,可得如下关系式
(13)
(14)
其中h是等腰腔一腰之高,f为透镜焦距。若腔内外媒介的折射率分别为n2、n1,则式(13-14)分别变为
(15)
(16)
其中式(13)或式(15)为前文所述的条纹分布律,结论获证。式(14)、(16)为利用此等倾干涉装置测量光波波长的公式。
2 几何约束条件及有限入射角范围对干涉的影响
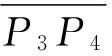
(17)
当玻璃折射率n2的取值范围在(1.56,1.62)之间,其临界反射角θc=arcsin(n1/n2)在(38°,40°)之间,当α=90°(对应于最普通最佳等腰直角劈)时,θ=(180°-α)/2=45°>θc,当折射角范围在i~(00,10),光线在底边BC界面发生全反射,而没有折射能量损失。

(18)
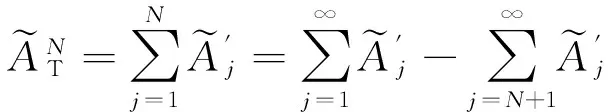
(19)
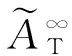
(20)
其中Δ为两者之相对误差,Δ=RN(2cosNδ-RN);相应地,条纹峰值的实际半值角宽度εN比理论的ε∞值有所增加,εN=ε∞(1+Δε)。我们可给出一组数据,使读者对此有一粗略的定量概念:腔体长宽尺寸a=h~1cm;波长λ~632.8nm;腔内光束折射角i的角度范围i~(00,10),反射回路达到N~29个,(即有限项数为30个);强度峰值相对偏差Δ~0.16,相应地半值角宽度较理论结果有所增加,而实际峰值强度较理论结果有所减弱。
3 应用前景
等腰劈的等倾干涉方式不仅可用于测入射光的未知波长,即对于F-P干涉技术具有等效性、替代性,而且还具有补充作用。以下略述它的一些新的特点与应用前景。
3.1 应用前景之一——全偏振光学谐振腔
等腰劈的等倾干涉方式可用于设计全偏振光学谐振腔,用以产生全偏振共振型极大输出光束。
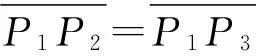
(21)
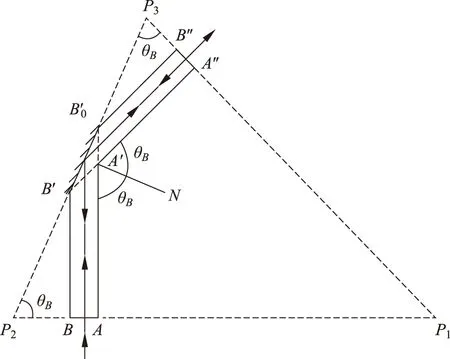
图4 全偏振输出光学谐振腔
全偏振共振输出条件是
(22)
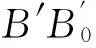
3.2 应用前景之二——二维微位移光学传感技术
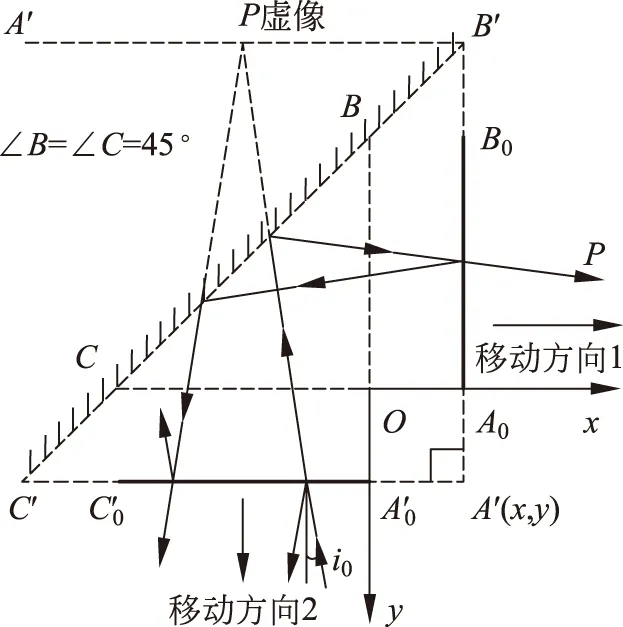
图5 二维位移光学传感示意图
4 总结与前瞻
大顶角等腰劈在入射光以特定角度范围横向入射时,将发生多光束等倾干涉,在干涉效果上等效于F-P干涉仪——在扩展光源照射下,将出现不等间隔的同心圆环形条纹。其干涉条纹形状一般说来是圆弧或圆弧在接收屏上的投影。当光源、薄膜、接收屏三者成对称关系时,条纹形状为明暗相间的圆环。影响干涉效果的诸因素也与薄膜干涉情形基本相同,其干涉条纹细锐,明暗对比强烈;干涉条纹的级数序列内高外低,环纹密度内疏外密。当腰上的高线长h增大时,干涉环纹由内向外移动。等腰劈等倾干涉技术不仅拓展了光学干涉的教学研究的内容与范围,还可能应用于全偏振光学谐振腔与维微位移光学传感器的设计。
(本文的先发论文[4]曾经赵凯华先生推荐至《光学学报》, 再经《光学学报》按协议遴选推荐至SPIE之《OpticalEngineering》发表,即文献[4])
[1]BornM,WolfE,PrinciplesofOptics[M]. 6thed.NewYork:PergamonPress. 1981. 291.
[2] 赵凯华,钟锡华. 光学[M]. 北京:北京大学出版社, 1984, 291-293.
[3] 钟锡华. 现代光学基础[M]. 北京:北京大学出版社, 2003年8月第一版,167-170.
[4]ZhouGuoquan,SuiShixian.Equalinclinationinterferenceprinciplesinarectangularcavityandinanisosceleswedge[J].OpticalEngineering, (SPIE), 1994, 33(9): 2922-2926.
[5] 周国全. 牛顿环干涉装置的若干变异结构[J]. 武汉大学学报(工学版), 2000, 33(5):110-112.ZhouGuoquan.SeveralvariantstructuresofinterferenceapparatusforNewton’srings[J].JournalofWuhanUniversity(Eng.Ed.), 2000, 33(5): 110-112.(inChinese)
[6] 周国全,郭长立.再论牛顿环干涉装置的若干变异结构[J]. 武汉大学学报 (理学版), 2005, 51(1):51-54.ZhouGuoquan,GuoChangli.SeveralmorevariantstructuresofinterferenceapparatusforNewton’srings[J].JournalofWuhanUniversity(Nat.Sci.Ed.), 2005, 51(1): 51-54. (inChinese)
[7] 周国全,隋士先.对角式与三角式光学干涉仪设计原理[J].武汉大学学报(工学版), 1993, 26(3):330-335.ZhouGuoquan,SuiShixian.Designprinciplesofdiagonalandtriangleopticalinterferometers[J].JournalofWuhanUniversity(Nat.Sci.Ed.), 1993, 26(3): 330-335. (inChinese)
[8] 周国全.牛顿型等厚直纹干涉及其变异结构[J].物理通报,2015(1): 31-34.ZhouGuoquan.TheequalthicknessinterferencefringesforseveralmoreNewton-typevariantinterferencestructures[J].PhysicsBulletin, 2015(1): 31-34. (inChinese)
[9] 周国全.正交柱面透镜的椭圆(双曲)型等厚干涉条纹[J].大学物理,2016,35(7):6-10.ZhouGuoquan.Theelliptic(hyperbola)distributionlawsofequal-thicknessinterferencesfortwocrossedconvex(concave)columnlens[J].CollegePhysics, 2016,35(7): 6-10. (inChinese)[10] 周国全.矩形腔等倾干涉原理[J].物理与工程,2017,27(6).ZhouGuoquan.Theequalinclinationinterferenceinarectangularcavity[J].PhysicsandEngineering, 2017, 27(6). (inChinese)
[11] 周国全,孙东振,彭获然.基于LabVIEW平台的新型二维微位移传感器设计[J]. 传感技术学报, 2015(4):607-612.ZhouGuoquan,SunDongzhen,Penghuoran.Anoveltwo-dimensionalmicro-displacementsensorbasedonLabVIEWplatform[J].ChineseJournalofSensorsandActuators, 2015(4): 607-612. (inChinese)
[12] 周国全,张斯磊.基于等倾干涉的二维微位移光学传感测距系统[J]. 武汉大学学报(理学版).2010, 56(5): 609-613.ZhouGuoquan,ZhangSilei.Atwo-dimensionalopticalmicro-displacementsensingandrangingsystembasedonnewequalinclinationinterferencestructure[J].JournalofWuhanUniversity(Nat.Sci.Ed.), 2010, 57(1): 609-613. (inChinese)
[13] 周国全,周一博.基于CMOS图像传感技术和等倾干涉的改进的二维微位移传感系统[J].武汉大学学报(工学版), 2017, 50(2):301-306.ZhouGuoquan,ZhouYibo.AnImprovedtwo-dimensionmicro-displacementsensorsystembasedonthetechniquesofCMOSimagesensorandequal-inclinationinterference[J].JournalofWuhanUniversity(Eng.Ed.), 2017, 50(2): 301-306. (inChinese)
[14]ZhouGuoquan,SunDongzhen.Anoveltwo-dimensionalmicro-displacementsensorbasedonanewopticalstructureforequal-inclinationinterference[C]. 2012, 2012SymposiumonPhotonicsandOptoelectronics, (SOPO),Shanghai.
■
THE EQUAL INCLINATION INTERFERENCE IN AN ISOSCELES TRIANGULAR WEDGE WITH A BIG VERTEX ANGLE
Zhou Guoquan Qi Ning
(School of Physics and Technology, Wuhan University, Wuhan Hubei 430072)
According to the optical wave theory about optical interference, the equal inclination interference in an isosceles triangular wedge with a big vertex angle has been concretely introduced and analyzed in detail; the interference conditions and the distribution laws of interference rings are deduced and discussed,which are in accordance with the observed phenomena in a verification experiment. On the other hand, the application possibilities of this interference principle in different fields of optical technology, especially in the field of optical micro-displacement sensor, are also discussed; and its subsidiarity to the pedagogical practices about optical interference, especially equal inclination interference, is emphasized; the teaching contents about the equal inclination interference are extended
optical interference; equal-inclination interference; interference rings; isosceles triangular wedge; optical resonant cavity; micro-displacement sensor
2017-06-05
高校教指委电动力学教学研究项目(项目编号: JZW-16-DD-15);中央高校教育教学改革专向项目—武汉大学“351人才计划”教学岗位项目。
周国全,男,副教授,研究方向为电磁场与光电子技术、非线性方程与孤子理论,zgq@whu.edu.cn。
周国全,祁宁. 大顶角等腰劈的等倾干涉原理[J]. 物理与工程,2017,27(5):65-70.

