仿鱼尾推进器在动力航向控制上的应用
袁 鹏,杨 晔,周国齐,刘作军
(1. 河北工业大学,天津 300132;2. 天津航海仪器研究所,天津 300131)
仿鱼尾推进器在动力航向控制上的应用
袁 鹏1,杨 晔2,周国齐1,刘作军1
(1. 河北工业大学,天津 300132;2. 天津航海仪器研究所,天津 300131)
传统的螺旋桨推进器工作噪声大,效率低,而仿鱼尾推进器技术有望改进这些不足,从而提出利用仿鱼尾推进动力定位的思想。通过对鱼尾推进模式和动力学的研究,设计出了最佳参数的仿鱼尾推进器。首先根据力的分解和拉格朗日动力学方程,计算出了前向推进力和各关节转矩,为课题研究奠定了力学基础;在动力定位控制研究中,通过惯性测量装置获取运动信息,采用卡尔曼滤波的数据融合算法实现姿态信息的解算,建立x方向上的空间运动模型并使用模糊自适应PID算法和传统PID算法仿真模拟。系统稳定性分析显示,PID控制存在14%的超调,而模糊自适应PID控制算法没有出现超调,两者的稳定时间均在240 s左右。最后由仿真分析验证模糊自适应PID算法更适合动力定位控制。
仿鱼尾推进器;动力定位;惯性测量;卡尔曼滤波;模糊自适应PID
鱼类凭借高效的鱼尾和鳍能在水中灵活游动和定位,而仿生鱼的研究开始于1994年,美国MIT研究小组研制出世界上第一条仿生金枪鱼。近年来对鱼尾动力学的研究已经相当成熟[1],从理论上解释了鱼尾工作时的高效性,但是把仿鱼尾推进器单独作为一种推进技术的研究为数不多。
动力定位系统是水下潜器和船舶的重要控制系统之一,它主要是利用推进器进行载体姿态的调整,并稳定在设定的位置。传统的螺旋桨推进器在船舶和水下潜器中广泛应用,然而长期以来其推进性能基本没有明显的提升。仿鱼尾推进器作为一种新的推进技术,主要的优点有推进效率高、机动性能好、噪音低、阻力小、桨舵合一、结构简单等。高效灵活的仿鱼尾推进器将会在动力定位中得到应用。本文主要研究基于仿鱼尾推进器动力定位的基础技术,即对载体姿态进行控制,使之保持在设定航向。
1 仿鱼尾推进器结构参数设计
本文选择鱼类中最常见的运动方式尾鳍摆动推进模式(BCF),如图1,它在游动时,仅仅有身体的后1/3在波动,前面的2/3几乎没有波动,然而它前进90%的推力也是由后1/3提供的。
在鱼尾的研究中,通常将前面载体部分看成刚体,它是依靠一个狭长而柔软的区域和尾部相连,这部分区域叫做尾柄,也可以看成尾鳍的一部分。影响尾鳍运动性能的结构参数主要有:
1)尾鳍形状:影响尾鳍形状的参数主要有尾鳍的面积S和展弦比L/C。根据试验研究,展弦比越大,推力就越大。

图1 BCF进模式Fig.1 Model of BCF propulsion
2)摆动部位关节数(N):摆动部分的关节决定尾鳍的柔软程度。N越大,尾鳍柔性就越大,游动就越灵活,但是整个运动效率降低。
3)摆动部分各关节的长度比:在这个值相对大的部位,关节的密度大,柔性就越大。
综合三个方面的考虑,本文的仿鱼尾推进器的实物结构如图2所示。

图2 仿鱼尾构Fig.2 Structure of fish-tail propeller
2 仿鱼尾推进器的动力学分析
鱼类可以在水中灵活地游动和悬停,主要是利用鱼尾平动和摆动的复合运动,调整运动方向和保持位置的稳定。动力定位是通过仿鱼尾推进器相互抵消外力扰动实现的,因此鱼尾受力分析是提供动力定位的理论基础[2]。为了简化力学分析,先进行几个假设:
➢ 鱼尾是理想刚体,不存在任何摩擦力和间隙;
➢ 尾鳍为质量分布均匀的薄板,质心为几何中心;
➢ 鱼尾的前端只有一个自由度。
根据以上假设,在研究平动的推力时将鱼尾看成一个质点,受力分析时先不考虑载体的受力,只考虑鱼尾的推力,且薄板在水中的阻力忽略不计。
2.1 推力分析及计算
运动时,鱼尾的推力主要由流体压力、升力、惯性力和前缘力等产生,其中尾鳍摆动时流体产生的压力和尾涡产生的升力是主要推力成分。
1)流体压力
流体压力主要是由鱼尾摆动形成涡流而产生,根据流体力学伯努利原理,会产生一个方向垂直于鱼尾表面的压力,为本体的前进提供推力,其定义为

式中:ρ为流体密度;V为鱼尾与流体的相对速度;S为鱼尾的表面积。
2)升力
鱼在水中运动时,根据大展弦比类机翼理论,尾部会受到来自流体的升力,升力的方向和运动方向相垂直,其定义为

式中:L为展长;C为弦长;α为鱼尾击水角度。
仿鱼尾推进力的计算主要包括尾鳍推进力和尾柄推进力的计算,设平动—摆动的运动规律表示为

则平动运动速度和摆动角速度则可以表示为
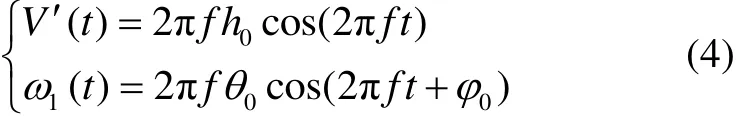
式中:h0为尾鳍平动运动最大幅值;θ0为尾鳍摆动最大幅值;f为摆动频率;φ0平动与摆动的最大相位差。以V0表示来流速度,则尾鳍相对流体速度为

由前面的分析可知:推进力主要分为流体压力产生的推进力和尾涡升力产生的推进力,分别建立模型并计算如下:
1)尾鳍推进力计算
设F1为作用在尾鳍表面上的流体压力,根据伯努利原理对该力的分析如图3所示。
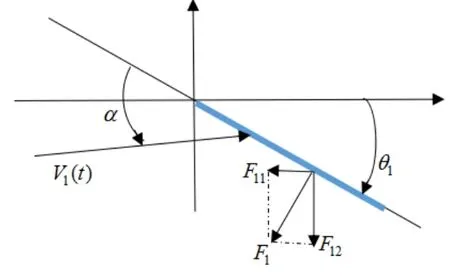
图3 尾鳍流体压力模型Fig.3 Fluid pressure model of caudal fin
由图3可知,尾鳍所受流体压力产生的推进力为

根据大展弦比类机翼理论,尾鳍的升力模型如图4所示。
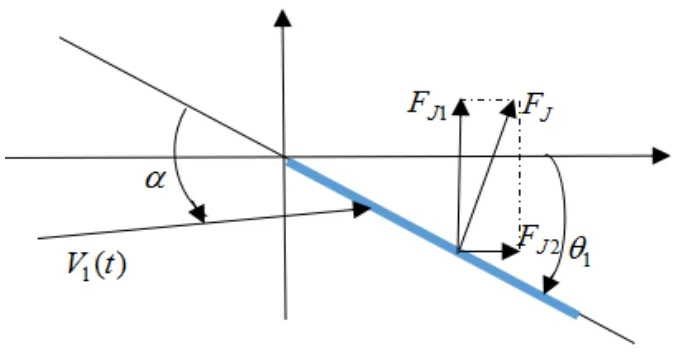
图4 尾鳍升力模型Fig.4 Lift model of caudal fin
由图4可得,由尾涡对尾鳍产生的升力而产生的推进力为

式中:L为尾鳍展长;C为尾鳍弦长。
综上分析可得,尾鳍产生的总推进力大小为

2)尾柄推进力计算
尾柄推进力的计算方法与尾鳍的计算同理。但是计算升力时,展长和弦长的乘积近似用尾柄的表面积来替代。因此可得,尾柄产生的总推进力大小为

式中:S2为尾柄表面积;r2为尾柄重心到鱼体转动关节的距离;A0为尾柄摆动幅值。
综上分析可得,仿鱼尾推进器产生总的推进力为

2.2 各关节转矩的分析及计算
利用拉格朗日法进行动力学分析[3],其方程为

式中:Ek为系统的动能;Ep为系统的势能;qi为广义坐标;尾柄和尾鳍的相对角位移分别为θ1、θ2;Qi为广义力,为尾柄和尾鳍的力矩;T为涡流反作用力对各个关节的力矩。
通过对式(11)的化简、整理可得到尾柄和尾鳍的转动力矩:

其中,尾鳍和尾柄长度分别为l1、l2,质量分别为。通过式(10)(12)可以求出应施加于尾柄和尾鳍关节的力矩和推力,保证系统运动加速度、速度的精确控制,减小外力对系统的冲击。
3 航向控制建模与仿真
3.1 基于卡尔曼滤波的姿态信息处理
本文使用的惯性测量装置是以STM32单片机为处理器,通过姿态传感器MPU9250对运动姿态进行检测,来提供俯仰角、横滚角和航向角等姿态信息。MPU9250包括三轴陀螺仪、三轴加速度计和三轴磁力计,每个传感器在所测量的参数上都有较高的性能,但也有一定的局限性,这些局限性会影响各个参数的精确度,这就需要对各个传感器的测量参数进行数据融合,研究出一种实时高效的姿态解算算法。
本文使用姿态漂移小、实时性好、能够实现自适应的卡尔曼滤波的数据融合算法[4-7],它是以系统的观测量作为输入,以系统的状态量估计值作为输出,利用系统噪声和观测噪声的协方差进行最优估计的数据处理方法。假设系统的状态向量和观测值可用下面公式表示:

式中:qn为当前状态的旋转四元数;A为状态变换矩阵;qn-1为下一个状态的旋转四元数;B为当前的输入系数矩阵;un当前输入;Zn为观测值;C为状态增益矩阵。对于姿态检测系统,陀螺仪的角度状态可用式(13)描述,加速度计和磁力计的对应角度值可作为观测反馈值。
每一次卡尔曼滤波计算输出状态都分为三个步骤:预测部分、观测部分、更新部分。1)预测部分

式中:Pn-1是前一个状态的协方差,根据式(17)(18)可以估算出本状态的旋转四元数。
2)观测部分
卡尔曼滤波还需要一个当前状态的观测值,如下式:

3)更新部分
这里要计算出一个差值(新息),其方程为

式中:R为测量噪声协方差矩阵,这里取单位阵I4×4·0.001。最终,得到后验旋转四元数:

和后验协方差矩阵:

增益矩阵K决定了最终的输出值qpo,n更倾向于预测值还是观测值[7]。为提高角速度的精度,还要进行温度传感器的补偿,因此在使用陀螺仪角速度计算状态旋转矩阵之前减去当前温度的零位漂移速度,最后得到卡尔曼滤波数据融合算法的流程图,如图5所示。
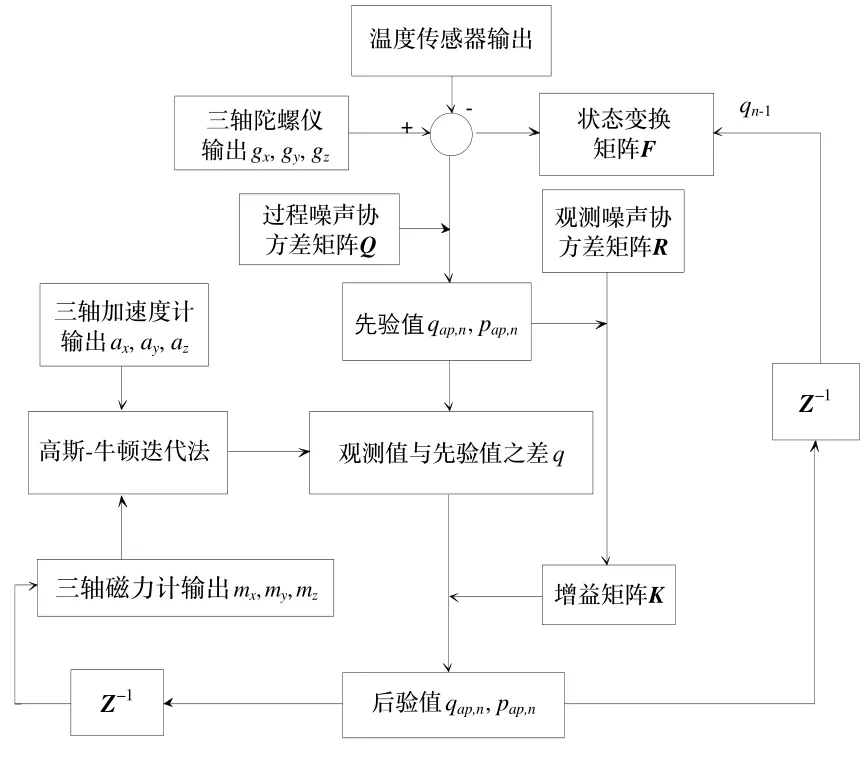
图5 卡尔曼滤波的数据融合算法的流程图Fig.5 Flow chart of data fusion algorithm based on Kalman filter
3.2 航向控制模型建立
仿鱼尾推进器能灵活地改变运动方向是实现动力定位的前提,而精确的方向运动控制需要建立航向控制运动模型[8-9]。本文主要是研究仿鱼尾推进的航向动力控制,因此需要建立一个关于输入是平均摆动角度θα,输出是航向偏转角度φp的模型,二者的关系如图6所示。
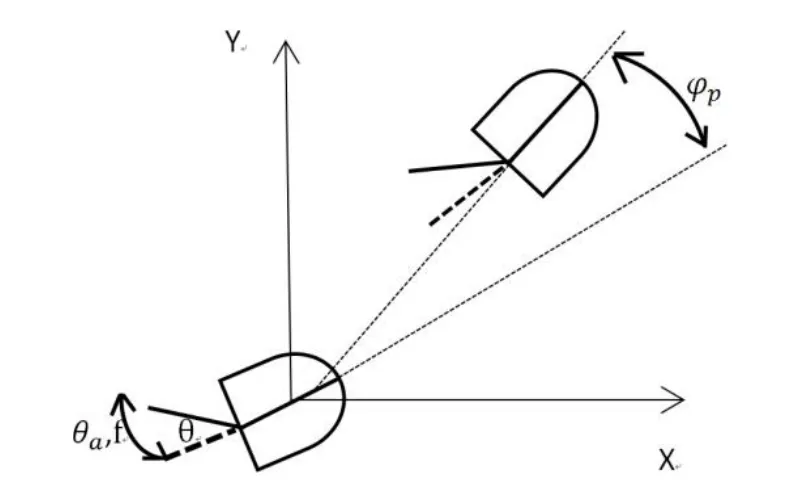
图6 仿鱼尾船运动示意图Fig.6 Swimming fish-like boat illustration
本文以仿鱼尾船水平面x方向的航向动力定位为研究对象,其空间运动数学模型为:
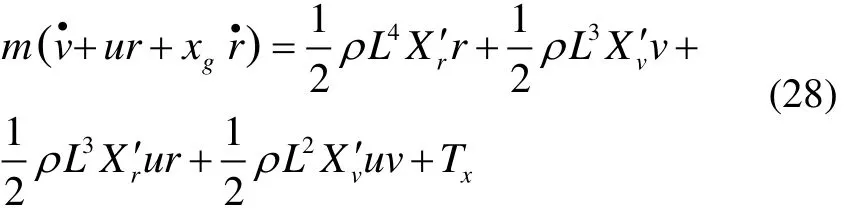
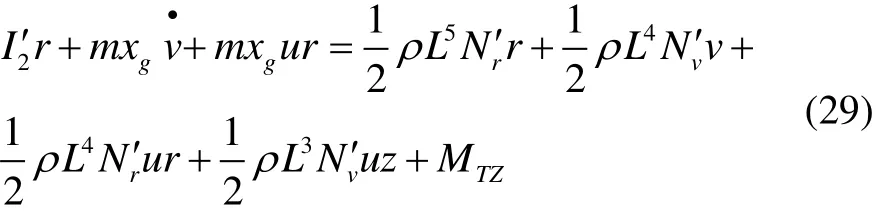
式中:ρ为海水密度;Ix、Iy、Iz为三轴向的转动惯量;xg、yg、zg为重心在载体坐标系上的坐标;Tx为推进器沿x轴向的推进力(2.1节已求);MTZ为Z轴的转矩(2.2节已求);′分别表示由速度、角速度、加速度及角加速度引起的纵向力和转矩的无因次相对应的系数。
模型在辨识过程中,仿鱼尾船的主要参数信息如表1所示。
辨识出的航向控制模型传递函数如式(30)所示:
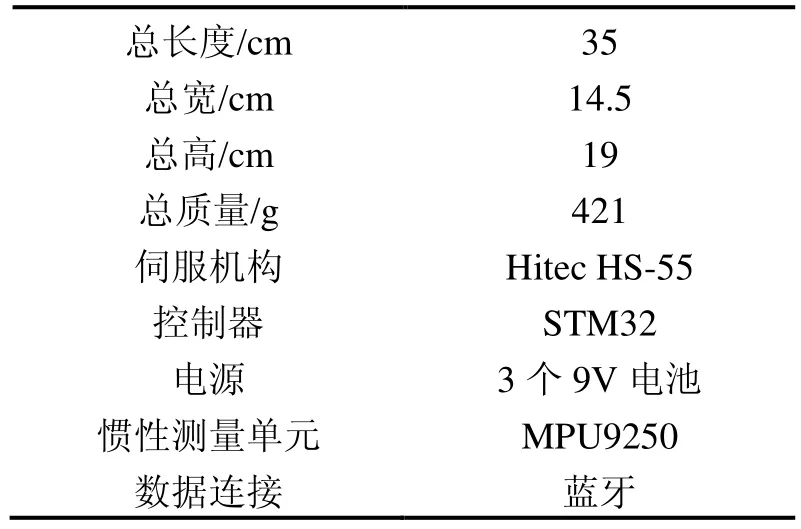
表1 仿鱼尾船的主要参数信息Tab.1 Main information of the fish-like boat

3.3 航向控制仿真验证及分析
根据式(31)可知,姿态航向模型是一个三阶的线性带滞后的传递函数,分别使用模糊自适应PID控制算法[10-11]和传统的PID控制算法在Matlab中的Simlink进行仿真[12]。设定稳定航向角度为50°,PID控制结构框图如图7所示,模糊自适应PID结构框图如图8所示,仿真结果如图9所示。
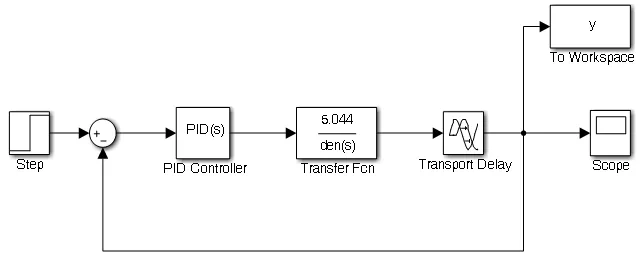
图7 PID控制结构框图Fig.7 Block diagram of PID control

图8 模糊自适应PID结构框图Fig.8 Block diagram of fuzzy adaptivePID

图9 仿真结果Fig.9 Simulation result
分析图9可以得到表2,传统PID控制算法结构简单,响应速度快,但是存在14%的超调量,而模糊自适应PID控制算法没有出现超调,且稳定时间基本一样在海洋、湖泊这样的复杂环境下,存着在洋流、风、浪等不定因素,所以对于控制系统的稳定性要求较高,而模糊自适应PID可以提高控制系统的稳定性能,使控制品质达到最佳。

表2 参数对比表Tab.2 Parameter comparison
4 结 论
本文通过对仿鱼尾推进器结构设计和动力学分析,将设计方案与仿鱼尾船航向动力定位结合,求出空间运动模型,并进行了模糊自适应PID控制算法仿真,验证了利用仿鱼尾推进器进行动力定位的可行性。本文是该课题方向上的初步研究,仿鱼尾推进器与动力定位结合还需要更多的理论论证和实验模拟。
(References):
[1] Xu Y, Mohseni K. A fish-like locomotion model in an ideal fluid with lateral-line-inspired background flow estimation[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. USA, 2014: 3181-3186.
[2] Kopman V, Laut J, Acquaviva F, et al. Dynamic modeling of a robotic fish propelled by a compliant tail[J]. IEEE Journal of Oceanic Engineering, 2014, 40(1): 209-221.
[3] Gu H, Zhao J, Hu D, et al. Analysis of propeller lift force based on FLUENT[C]//IEEE International Conference on Aircraft Utility Systems. Beijing, 2016: 119-123.
[4] Jian L, Lei Y, Cai Y, et al. Multi-sensor data fusion algorithm based on fuzzy adaptive Kalman filter[C]//IEEE Control Conference. Italy, 2013: 4523-4527.
[5] 余星. 基于捷联惯性的水下载体姿态检测系统研制[D].杭州: 杭州电子科技大学, 2013.
[6] Li J, Xia G. The application of an extended Kalman filter in the dynamic positioning system[C]//12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery. Changsha, 2016: 1945-1949.
[7] McFarland C J, Harris Z J, Whitcomb L L. Development of and preliminary results with an extended Kalman filter for the estimation of the translational and angular velocity of underwater vehicles[J]. 2014 Oceans - St. John's. 2015: 1-8.
[8] Karakasis N. Active yaw control in a horizonta axis wind system without requiring wind direction measurment[C]//IEEE Conference Publications. Xi’an, 2015: 1444-1449.
[9] Xue Tao, Zhao Yang, Cui Sheng-guo, et al. Design and implementation of manned submersible semi physical simulation system[C]//International Conference on Robotics and Biomimetics. USA, 2016: 155-160.
[10] Lukichev D V, Demidova G L, Brock S. Fuzzy adaptive PID control for two-mass servo-drive system with elasticcity and friction[C]//2015 IEEE 2ndInternational Conference on Cyberetics. California, 2015: 443-448.
[11] Lei Yan-min, Du Li-min, Feng Zhi-bin. Motion control of robot based on fuzzy adaptive PID algorithm[C]//2013 3rd International Conference on Computer Science and Network Technology. Network, 2013: 1310-1313.
[12] 谢克峰, 张合, 唐玉发, 等. 伸缩式鸭舵二维修正策略和修正能力[J]. 中国惯性技术学报, 2015, 23(4): 477-482.Xie Ke-feng, Zhang He, Tang Yu-fa, et al. Two-dimension correction strategy and capability for retractable canard[J]. Journal of Chinese Inertial Technology, 2015, 23(4):477-482.
Application of fish-tail propeller on dynamic heading control
YUAN Peng1, YANG Ye2, ZHUO Guo-qi1, LIU Zuo-jun1
(1. Hebei University of Technology, Tianjin 300132, China;2. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)
In view that conventional propellers are featured by large working noise and low efficiency, while the fish-tail propeller technology is expected to improve these shortages, the idea of using fish-tail propeller to realize the ship’s dynamic positioning is proposed. Based on the study of the fish-tail propulsion model and the dynamic features, a fish-tail propeller with optimum parameters is designed. Firstly, according to the force’s decomposition and the Lagrange dynamics equation, the forward propulsion force and each joint torque are calculated, which lays a mechanical foundation for the subject research. In studying the dynamic positioning control, the motion information is obtained by inertial measurement device, and the data fusion algorithm based on Kalman filter is used to solve the attitude information. The spatial motion model in X direction is established, and the fuzzy adaptive PID algorithm and the traditional PID algorithm are used to conduct the simulations. The system stability simulation analysis shows that the PID control has 14%overshoot, while the fuzzy adaptive PID has no overshoot, and both the stability times are about 240 s, which show that the fuzzy adaptive PID algorithm is more suitable for dynamic positioning control.
fish-tail propeller; dynamic positioning; inertial measurement; Kalman filter; fuzzy adaptive PID
TP273
:A
1005-6734(2017)03-0399-06
10.13695/j.cnki.12-1222/o3.2017.03.022
2017-03-26;
:2017-05-26
国家自然科学基金项目(61174009);国家自然科学基金项目(61203076)
袁鹏(1992—),男,硕士研究生,从事水下推进技术研究。E-mail: yuanpeng_215@sina.com
联 系 人:杨晔(1968—),男,高级工程师,从事惯性导航技术研究。E-mail: 13920448585@163.com

