再谈“光滑斜面上滑块下滑问题”的求解方法
于志明 刘丽丽
(连云港师范高等专科学校物理系 江苏 连云港 222006)

再谈“光滑斜面上滑块下滑问题”的求解方法
于志明 刘丽丽
(连云港师范高等专科学校物理系 江苏 连云港 222006)
给出光滑斜面上滑块下滑问题中相对运动关系,利用守恒定律和拉格朗日方程对问题进行求解.建议一些优秀的高中生学习初步的分析力学知识,以提高他们处理复杂力学问题的能力.
斜面 滑块 动量守恒 机械能守恒 拉格朗日方程
文献[1]研究了这样一道力学题:如图1所示,一质量为M,倾角为θ的光滑斜面,放置在光滑的水平面上,另一质量为m的滑块从斜面顶端释放.试求:
(1)斜面的加速度aM;
(2)滑块相对斜面的加速度a相对;
(3)滑块的加速度am.

图1 题图
在文献[1]中分别利用非惯性系动力学方程和受力分析图的方法给出了此题的两种解法.这是一道考查学生物理学素养的好题,此题的其他方面的问题也受到了人们的关注[2].本文先建立滑块与斜面的相对运动关系,然后给出此题的两种解法:一种解法是利用守恒定律,这是牛顿力学中求解这道题的比较简单的方法;另一种解法是运用拉格朗日方程,这种方法要求学生掌握初步的分析力学知识.我们认为,在今天的高中物理教学中,牛顿力学受到了高度关注,而对牛顿力学之后发展起来的力学高峰——分析力学,没有给予适当的关注.我们建议,当前的一些优秀的高中生学习初步的分析力学知识,如虚功原理和保守力系的拉格朗日方程,这对于丰富他们的物理学知识,提高他们处理复杂力学问题的能力,使他们在各种考试竞赛中取得好成绩是大有帮助的[3],这也可以作为部分高中物理教学改革发展的一个方向.
1 滑块与斜面相对运动关系的数学表示
建立如图2所示的直角坐标系O-xy,该坐标系在空间固定不动,其原点在刚开始运动时斜面的顶点.设某一时刻斜面右边线的水平坐标为X,滑块在斜面上下滑的距离为s,则此时滑块在直角坐标系O-xy中的坐标为
x=X-scosθ
(1)
y=ssinθ
(2)
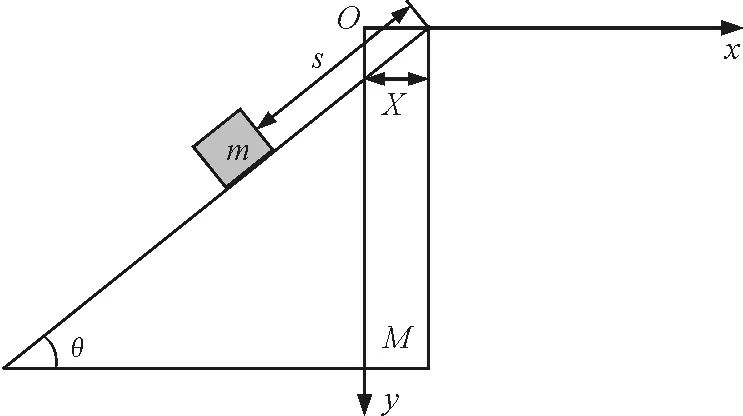
图2 建立直角坐标系
式(1)、(2)也是滑块与斜面相对运动的坐标关系的数学表示.将式(1)、(2)的两边分别对时间t求导数得
vx=vM-v相对cosθ
(3)
vy=v相对sinθ
(4)
式(3)、(4)中的vx,vy是滑块的速度在直角坐标系O-xy的两坐标轴上的投影,vM是斜面在水平面上运动的速度,v相对是滑块在斜面上下滑的相对速度.式(3)、(4)就是滑块与斜面相对运动的速度关系的数学表示.将式(3)、(4)的两边再对时间t求导数得
ax=aM-a相对cosθ
(5)
ay=a相对sinθ
(6)
式(5)、(6)中的ax,ay是滑块的加速度在直角坐标系O-xy的两坐标轴上的投影,aM是斜面在水平面上运动的加速度,a相对是滑块在斜面上下滑的相对加速度.式(5)、(6)就是滑块与斜面相对运动的加速度关系的数学示.
以上得到的这些相对运动关系,在这道题的求解过程中是十分重要的.
2 利用守恒定律来求解
我们知道由滑块和斜面组成的系统在直角坐标系O-xy中的水平方向的动量是守恒的,由此得
mvx+MvM=0
(7)
由滑块和斜面组成的系统在直角坐标系O-xy中的机械能是守恒的,由此得
(8)
由式(3)、(7)可得
(9)
将式(9)代入式(7)得
(10)
将式(4)、(9)、(10)代入式(8)得
(11)
将式(11)两边对时间t求导数可得
(12)
将式(9)两边对时间t求导可得
(13)
将式(12)代入式(13)得
(14)
将式(12)、(14)代入式(5)、(6)得
(15)
(16)
所以
(17)
在已经求得滑块和斜面在直角坐标系O-xy中运动的加速度以后,我们还可以求得滑块和斜面以及斜面和水平面之间的相互作用力.
3 利用拉格朗日方程来求解
我们大家知道,分析力学是在牛顿力学之后力学理论发展的一个里程碑,对于求解比较复杂的力学问题,分析力学的方法要比牛顿力学的方法优越得多.
在分析力学中,受到理想约束(如光滑面、光滑线、光滑铰链、刚性杆、不可伸长的绳的约束)的保守系的基本动力学方程为拉格朗日方程,下边我们用拉格朗日方程来求解这道题.
以滑块和斜面作为研究的系统,该系统是受到理想约束的保守系.要确定滑块和斜面的空间位置只要2个独立参量,我们就选择图2中的X和s,显然由X就确定了斜面的位置,而由s就确定了滑块相对于斜面的位置.
系统的动能为
(18)
将式(3)、(4)代入得
(19)
系统的势能可以表示为
V=-mgssinθ
(20)
系统的拉格朗日函数为
(21)
将L代入拉格朗日方程
(22)
和
(23)
得
m(aM-a相对cosθ)+MaM=0
(24)
a相对-aMcosθ-gsinθ=0
(25)
由式(24)、(25)可解得a相对和aM,结果同前.其余略.
试想如果我们将图1所示的问题改为图3所示的问题,这时我们用拉格朗日方程来求解比用牛顿
力学来求解就要更加方便了.
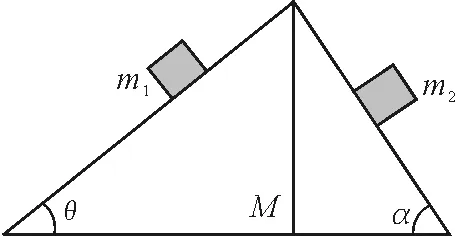
图3 拓展
1 吴好.用受力分析图分析光滑斜面上滑块下滑问题.中学物理,2012,30(19):73~74
2 何述平.一个力学问题的一对内力做功的探讨.物理教师,2012,33(8):43~44
3 袁张瑾.竞赛中巧用“元功法”求解的平衡问题.物理教学,2012,34(8):56~57
2016-12-30)

