一道全国物理竞赛试题的简解及其引起的思考
蔡 阳 黄绍书
(六盘水市第23中学 贵州 六盘水 553001)

一道全国物理竞赛试题的简解及其引起的思考
蔡 阳 黄绍书
(六盘水市第23中学 贵州 六盘水 553001)
根据角动量守恒定律,对一道全国物理竞赛试题给出巧妙而简捷的解答,并对由此引起的一些相关问题予以讨论.
角动量守恒定律 物理竞赛 巧解 讨论
1 问题的提出
第八届全国中学生物理竞赛已经过去25年,然其预赛第一试试题第5题,如今想起依然历久弥新.赛场监考看到的情景,仅有少数参赛选手能零散地列出个别方程组,多数甚至无从下笔.本次竞赛后一周,中央电视台一套节目特邀有关专家针对该题作专题剖析,可见其难度之大.
【题目】如图1所示,一水平放置的圆环形刚性窄槽固定在桌面上,槽内嵌着3个大小相同的刚性小球,它们的质量分别是m1,m2和m3,且m2=m3=2m1.小球与槽的两壁刚好接触而它们之间的摩擦可忽略不计.开始时,3球处在槽中Ⅰ,Ⅱ,Ⅲ的位置,彼此间距离相等;m2和m3静止,m1以初速度

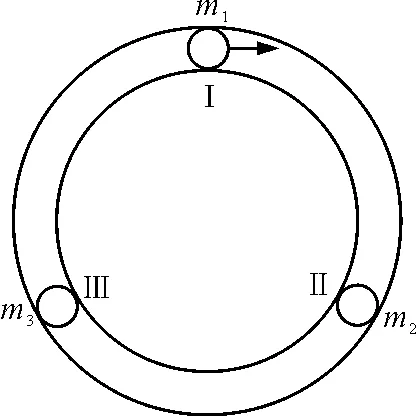
图1 题目题图
根据竞赛组委会提供的参考答案以及目前相关网站搜索的信息,这道题形成共识的解答思路,就是根据动量守恒定律和机械能守恒定律计算出各个小球之间的每次相互碰撞前后的速度,分析出各次相互碰撞的位置和相邻两次碰撞之间经历的时间,从而得出问题的解.由于要多次涉及高次方程组的求解和多次碰撞的复杂性,使得问题的解答特别困难.
2 试题的简解
根据质点和质点组角动量守恒定律[1]可知,由于窄槽对3个小球组成的系统作用力的力矩为零,因此系统在运动过程中的角动量守恒.
设系统运动过程中质心速度为v,那么
Rm1v0=R(m1+m2+m3)v
所以
因此
3 共识普遍解[2,3]
由于各个小球之间的碰撞均为弹性碰撞,因此,碰撞过程中系统的动量和机械能都守恒.

得
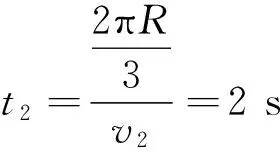

得

至此,3个小球组成的系统相对于原位置均分别改变了120°,且速度与初始状态相同.故再经过这样两个相同的过程就完成一个系统运动周期T,因此
T=3(t1+t2+t3+t4)=20 s
4 思考与讨论
“简解”与“普遍解”的计算量和繁简程度存在很大的反差.由此,引起一些相关问题值得讨论.
(1)系统的运动周期与各小球的初始位置无关,但初始位置对“普遍解”的计算复杂性有较大的影响.
(2)各个小球之间的碰撞如果是非弹性碰撞,那么不存在系统运动的周期问题,因为系统不可能恢复到初始状态.
(3)质点组角动量守恒定律,在特定条件下可理解为切线方向的动量守恒定律.
1 漆安慎, 杜婵英. 力学. 北京: 高等教育出版社, 2005. 167~178
2 第八届全国中学生物理竞赛预赛第一试试题参考答案及评分标准
3 网络.http://www.1010jiajiao.com/gzwl/
2016-12-08)

