由卷积想到的计量单位及相关物理概念
陈希有, 李冠林, 刘凤春, 董维杰
(大连理工大学 电气工程学院, 辽宁 大连 116023)
由卷积想到的计量单位及相关物理概念
陈希有, 李冠林, 刘凤春, 董维杰
(大连理工大学 电气工程学院, 辽宁 大连 116023)
本文结合电路理论中卷积表达式和物理方程的量纲平衡原理,分别剖析了单位冲激响应h(t)和单位阶跃响应s(t)的计量单位,以及这些响应的实际含义和相关物理概念。强调了它们都是响应与激励的某种比值,不是普通意义上的响应电流或响应电压,因此其单位既不是电流的单位,也不是电压的单位。由此还延伸讨论了复频域中若干量的计量单位和相关物理概念问题。
卷积; 单位冲激响应;单位阶跃响应;计量单位。
0 引言
根据电路理论,设某线性电路的单位冲激响应为h(t),那么它在任意激励e(t)(电压或电流)作用下产生的零状态响应r(t)(电压或电流),可用卷积积分表示为
(1)
式中λ表示沿时间轴的积分变量,与时间具有相同单位,例如s。
问题1:如果激励是电流,单位A;响应是电压,单位V,那么h(t)的单位应该是什么,才能由积分得到响应电压的单位V?
回答:按照单位的乘除运算规则,h(t)的单位可根据式(1)并利用下式导出:

(2)
显然h(t)的单位既不是电流的单位,也不是电压的单位。
问题2:众所周知,单位冲激响应h(t)与单位阶跃响应s(t)满足如下导数关系:
(3)
那么s(t)的单位又应该是什么,才能得到h(t)的单位Ω/s呢?
回答:按照单位的乘除运算规则,s(t)的单位可由下式导出:

(4)
显然,单位阶跃响应s(t)的单位既不是电流的单位,也不是电压的单位,它在这里却与电阻的单位相同。
问题3:如何定义 和 才能得到上述正确的单位呢?
接下来将分步理清上述量的单位问题,并阐述相关物理概念。
1 单位阶跃响应s(t)的单位
零状态条件下,电路在单位阶跃激励作用下产生的响应,称为单位阶跃响应,用符号s(t)表示。本文特别强调:这个单位阶跃响应,应该被理解成阶跃响应与阶跃激励幅值之比,不是通常意义上的响应电流或响应电压。即,
(5)
分母中阶跃激励的幅值包括数值和单位,例如10 V、8 A。如果激励是电流,单位为A;响应是电压,单位为V,那么s(t)的单位就是V/A=Ω,与式(4)相同。
这就像理解速度的定义一样:单位时间内物体运动的距离,虽然最终量度是距离,但速度的单位是m/s,而不是m。
根据激励与响应是电流还是电压,单位阶跃响应s(t)有表1所示的四种情况。文献[1]也表明了这种观点(p.448-449)。

表1 单位阶跃响应s(t)的单位
使用带有上述单位的s(t),电路对任意幅值阶跃激励的零状态响应,便等于该阶跃激励的幅值与s(t)的乘积。例如10 A×e(t)电流源产生的响应电压为u(t)=10 A×s(t),等号右边的单位是A×Ω=V,自然是电压的单位。
2 单位冲激函数δ(t)和冲激强度的单位
在电路理论中,单位冲激函数δ(t)定义为
(6)
对于式(6)的下部,由于dt的单位是s,等号右边的1是纯数,因此δ(t)本身具有时间的倒量纲,单位为1/s=s-1,即Hz。这一点还可以从δ(t)与ε(t)的关系中得到进一步理解:
(7)
由于ε(t)本身是无量纲的函数,显然δ(t)的单位只能是1/s=s-1。这一点在教学时必须加以明确,否则容易出现量纲不平衡现象。
明确了δ(t)的量纲和单位之后,冲激强度(即δ(t)前面的系数,最好叫冲激量)的单位也就容易确定了。例如i(t)=Qδ(t),冲激强度Q的单位是As=C(库仑),即Q代表电荷,表示在t=0这一瞬间,有量值为Q的电荷从电路的某处流过;对偶地,当冲激函数是电压时,即u(t)=ψδ(t),则冲激强度ψ的单位是Vs=Wb(韦伯),即ψ代表磁链。类似的表述见文献[2](p.237),文献[3](p.305,p.308)。
带有数值的下述表示方法是正确的:i(t)=5C×δ(t),u(t)=2Wb×δ(t)。这里的5C和2Wb,不仅意味着使用了正确的单位,更重要的是它们代表了冲激强度的物理概念:电荷与磁链。
相比之下,值得引起注意的是:下面的表示方法是不严密的,从量纲上看甚至是错误的:i(t)=5δ(t) A(这里的A要与δ(t)的单位进行乘法运算,结果不再是电流的单位),is(t)=δ(t),us(t)=δ(t)。注意:仅δ(t)不能作为激励电流或激励电压,因为它不具有电流或电压的量纲。
因此,只要记住δ(t)本身是有量纲和单位的,据此导出的各种方程就不会出现量纲不平衡问题。
3 单位冲激响应h(t)的单位
零状态条件下,电路在单位冲激激励作用下产生的响应,称为单位冲激响应,用符号h(t)表示。本文特别强调:这个定义也应该从比值的角度来理解,即冲激响应与冲激激励的冲激强度之比。不是普通意义上的响应电流或响应电压。即,
(8)
考虑到激励和响应都可能是电压或电流,因此单位冲激响应h(t)有表2中的四种情况。文献[1]也表明了此观点(p.464)。

表2 单位冲激响应h(t)的单位
上述h(t)的单位实际就是s(t)的单位除以时间的单位,这正好符合式(3)所包含的单位关系。
只有遵循表2中h(t)的单位规律,计算卷积积分时,才不会出现量纲上的错误。
使用带有上述单位的h(t),电路对任意强度的冲激激励产生的响应,便等于该冲激强度与h(t)的乘积。例如,设激励为电流,响应为电压,单位冲激响应为h(t),那么h(t)的单位便是Ω/s。当激励电流为is=5C×δ(t)时,冲激电压响应为u(t)=5C×h(t)。等式右边的单位是C×Ω/s=V,它自然就是电压的单位,与左边一致。
小结:①s(t)与h(t)都是响应与激励的某种比值,不是普通意义上的响应电压或电流。前者是阶跃响应与引起该响应的阶跃激励幅值(单位V或A)之比;后者是冲激响应与引起该响应的冲激激励的冲激强度(单位C或Wb)之比;②只有把它们都理解成比值,才能在出现它们的方程中,保持量纲平衡;③在任何一对(指电压或电流)激励和响应下,s(t)与h(t)的单位都是不同的,并且都不是电压的单位或电流的单位;④不宜写成形如u(t)=s(t),或i(t)=h(t)这样的表达式,因为这些只代表数值上相等,不代表单位相同,量纲不能平衡。
鉴于s(t)和h(t)的单位都不是电压的单位或电流的单位,所以最好不要称它们为响应,因为在大多数教材中,已把响应定义成电路中的电压或电流这样的物理量。文献[1]和[4]将它们分别称为单位阶跃特性和单位冲激特性,以示与响应在物理概念上的区别。
【示例】 图1所示电路,已知R=10 Ω,C=0.2 F,uS(t)=60 e-t/τε(t)V。写出用卷积计算零状态响应u(t)和i(t)的表达式。

图1 示例图
【解】 先设激励为阶跃电压,即uS(t)=Uε(t)。由三要素公式可求得阶跃响应分别为
u(t)=U(1-e-t/τ)ε(t)
式中时间常数τ=RC=2 s。
将它们分别除以U得到电压与电流的单位阶跃响应(或称单位阶跃特性):
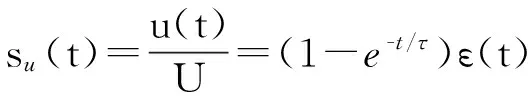

然后将阶跃响应对时间求导,得到电压与电流的单位冲激响应(或称单位冲激特性):
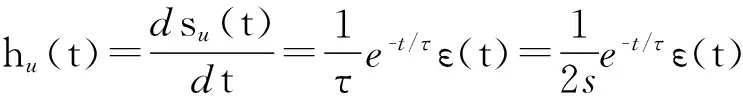
(9)
单位S/s
(10)
也可首先令uS(t)=ψδ(t),计算冲激响应,结果它们分别是,
再分别除以冲激强度ψ,得到分别与式(9)和式(10)一致的结果。
将上述冲激响应代入卷积公式(1),并考虑在积分区间内,ε(t-λ)=1,ε(t)=1,省略不写,因此当uS(t)=60 Ve-t/τε(t)时,电压与电流响应的卷积计算公式分别为
由于dλ的单位为s,所以上两式右边的单位分别为V和A,与所表达的等式左边的响应变量的单位完全一致,满足量纲平衡规律。
以上是为了说明单位的使用问题,才将u(t)和i(t)按照并行的步骤进行计算的。此外,还可以先求出电压u(t),然后按照i(t)=Cdu/dt的关系求出i(t)。
4 复频域中量的单位问题
卷积运算是积分运算,由此联想到同样是积分运算的拉普拉斯变换中的单位问题。
(1)象函数的单位
在电路理论中,拉普拉斯变换定义为
(11)
这里的斜体s表示复频率,具有时间的倒量纲,单位为s-1,即Hz。
由于dt的单位是s,所以象函数F(s)的单位是时域中f(t)(电压或电流)的单位乘以时间的单位s。如果时域中是电流,那么F(s)的单位就是As,即电荷的单位C(库仑);如果是电压,那么F(s)的单位就是Vs,即磁通的单位Wb(韦伯)[4]。
(2)待定系数的单位
在象函数的展开式中,如果是一阶极点,那么对应待定系数的单位就是时域中电压或电流的单位;如果是二阶或二阶以上的极点,情况则不然。例如,设某电容电压的象函数及其展开式为
分母中的1并不是纯数,它的单位s-1。为不与表示复频率的斜体 混淆,这里省略了s-1。
经计算,待定系数A1=2 V,A3=-1 V,它们与各自的分母运算后,得到的单位都是Vs。然而,A2的单位与A1、A3不同,因为
所以A2的单位是UC(s)的单位乘以s-2,即Vs×s-2=V s-1,这样从A2/(s+1)2才能得出单位Vs,也就是UC(s)所应有的单位。
(3)附加电源的单位
在非零初始条件下,电容和电感的复频域模型中含有附加电源,它们的单位与时域中电源的单位不同,附加电压源的单位与电压象函数单位相同;附加电流源的单位与电流象函数相同。这可以通过附加电源的具体表达式得到验证:
(a) 电容的附加电流源为CuC(0_),
单位:F×V=(C/V)×V=C(库仑);
(b) 电容的附加电压源为uC(0_)/s,
单位:V/s-1=Vs=Wb(韦伯);
(c) 电感的附加电压源为LiL(0_),
单位:H×A=(Wb/A)×A=Wb(韦伯);
(d) 电感的附加电流源为iL(0_)/s,
单位:A/s-1=As=C(库仑)。
(4)网络函数H(s)及其反变换h(t)的单位
网络函数定义为零状态响应的象函数与激励的象函数之比,有四种情况,见表3。

表3 复频域网络函数H(s)的单位
网络函数的拉普拉斯反变换就是单位冲激响应(或单位冲激特性),即
(12)
由于ds的单位是1/s,因此按照拉氏反变换得到的h(t)的单位分别是1/s、Ω/s、S/s和1/s。这与第3节的分析结果完全相同,相互印证。
5 结语
通过以上分析不难得出以下结论:
(1)不同于数学和纯信号理论问题,电路中的许多函数或变量都有确定的物理含义,所以应该正确使用它们的计量单位。
(2)保持电路方程的量纲平衡是重要的,可以通过检查量纲平衡性,来检验方程的正确性,使方程表达的物理概念更加清楚。
(3)单位冲激响应h(t)的计量单位,既不是电流的单位,也不是电压的单位。否则,在应用卷积计算零状态响应时,就不能得出电压或电流的单位。
(4)早点让学生养成使用单位的好习惯,要比事后更正坏习惯会更好。
(5)当前,工程教育日益得到重视。注重量纲平衡,正确使用物理量的单位,是在教学和教材中落实工程教育思想的重要内容,有助于培养学生严谨的学术态度和正确的工程观点。
(6)全面使用量的单位,在教学上和出版上可能存在不便,但在关键内容上,应该做到严谨规范。本文仅就卷积积分联想到某些量的计量单位问题进行了讨论,类似的问题是广泛存在的,教学时应给予必要考虑。文献[1]和[5]都是很好地使用物理量计量单位的我国教材和美国教材,可供参考。
[1] 许道展,程桂敏,王铁奎主编,俞大光主审. 电路基础(上册)[M].北京:中国计量出版社,1989年5月。
(陈希有等文)
[2] 孙雨耕. 电路基础理论[M]. 北京:高等教育出版社,2011年5月。
[3] 李瀚荪. 简明电路分析基础[M]. 北京:高等教育出版社,2002年7月。
[4] 陈希有. 电路理论教程[M].北京:高等教育出版社,2013年8月。
[5] 原著 Robert L. Boylestad, 翻译陈希有,张新燕,李冠林等. Introductory Circuit Analysis(电路分析导论)(原著第12版) [M]. 北京:机械工业出版社,2014年10月。
Some Measurement Units and Related Concepts Induced by Convolution
CHEN Xi-you,LI Guan-lin,LIU Feng-chun,DONG Wei-jie
(SchoolofElectricalEngineering,DalianUniversityofTechnology,Dalian116024,China)
Combined with the convolution expression in circuit theory and the dimensional balance principles of the physical equations, some measurement units of the unit impulse response and unit step response , as well as the practical implications of these responses and related concepts are analyzed. It is emphasized that they are both some kind of ratios of the response and the excitation, not the ordinary senses of the response current or voltage, so their units are neither the unit of current nor the unit of voltage. In addition, the measurement units of several quantities in the complex frequency domain and related concepts are also discussed.
convolution; unit impulse response; unit step response; measurement unit
2016-09-03;
2016-11-24
陈希有(1962-),男,博士,教授,主要从事电路和电工技术教学以及电力电子技术研究,E-mail: chenxy@dlut.edu.cn
A
1008-0686(2017)04-0036-05
图书分类号: TM13
——以匀加速直线运动公式为例

