基于意识作用的复杂网络上SIS模型的稳定性

赵爱民，陶佳琪，刘桂荣

(山西大学 数学科学学院，山西 太原 030006)

基于意识作用的复杂网络上SIS模型的稳定性

赵爱民，陶佳琪，刘桂荣

(山西大学 数学科学学院，山西 太原 030006)

研究三种意识对疾病传播的影响,建立了无标度网络上的SIS模型,并得到了该模型无病平衡点的稳定性及传播阈值。结果表明局部意识和接触意识可以提高传播率的阈值,全部意识对无病平衡点的稳定性及传播阈值没有影响。最后利用数值模拟验证了理论结果。

复杂网络;SIS模型;意识;阈值

0 引言

近年来,传染病的频发对人类造成了物质上和精神上的损害。 建立传染病动力学模型可以很好地研究疾病的分布情况和传播规律,便于更有效地预防和控制疾病传播。 传统的均匀混合传染病动力学模型认为所有个体的接触都是等可能的,显然忽略了个体行为的影响。 复杂网络上传染病动力学模型更符合实际[1]。 目前基于网络传染病的动力学模型中很少考虑到疾病信息对于疾病传播的影响。 但是,疾病信息的传播会导致人们疾病意识的增强,从而采取自我保护措施,例如勤洗手、佩戴口罩[2-3]等。

文[4]考虑了三种意识对疾病传播的影响。 假设一个易感者被一个染病邻居传染的概率只与易感者的度有关,但这是不合理的。 显然,一个易感者被一个染病邻居传染的概率与易感者和染病者的度都有关系。 基于上述研究背景,本文考虑意识作用下的复杂网络上的SIS模型。

1 模型建立

(1)

令Y表示与易感节点i连边的一个染病邻居j的度,则该染病邻居的度为m的概率为

(2)

由(1)和(2),度为k的易感节点i被一个染病邻居j传染的概率为:

(3)

令θ表示一个易感者节点一条边连接到染病者节点的概率,则

(4)

令Xk是一个随机变量,表示一个度为k的易感者节点的染病邻居数。则他有s(0≤s≤k)个染病邻居和k-s个易感者邻居的概率为:

(5)

由(3)式,如果一个度为k的易感者的染病邻居数为s,那么他被传染的概率为:

由(4)和(5),一个度为k的易感者被传染的概率为:

(6)

离散的动力学模型为:

ρk(t+1)=(1-γ)ρk(t)+(1-ρk(t))Θk.

考虑[t,t+Δt]上的动力学模型,并结合(6)式可得:

ρk(t+Δt)-ρk(t)=-γΔtρk(t)+(1-ρk(t))·

(7)

利用洛必达法则对上式求极限得到:

(8)

我们定义M(l)=E(elXk)=(θel+1-θ)k,l∈(-∞,+∞). 从而,

M′(0)=E(Xk)=kθ,

(9)

(10)

对(7)式等号两边同时除以Δt,令Δt→0并结合(8)-(10)可得:

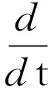
(11)

2 稳定性及传播阈值

注意到在(11)式中,

(k(θel+1-θ)k-1θel)(α1)|l=0=

[kθ((k-1)(θel+1-θ)k-2θe2l+(θel+1-θ)k-1el)](α1-1)|l=0=

(*+kθ(θel+1-θ)k-1el)|l=0=(*|l=0+kθ),

其中*是θ的高次项。从而,可得到系统(11)在无病平衡点处的线性化系统为:

(12)

线性系统(12)的系数矩阵为:

其中fk=ψk(k-a/kα1-1),gk=kpkβk/〈k〉.进一步,

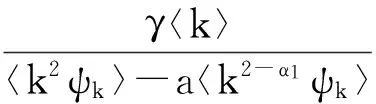
(13)

注:上述结果可知,全局意识对无病平衡点的稳定性及传播阈值没有影响。 局部意识和接触意识可以提高传播率的阈值。

3 数值模拟

这一部分我们将进行数值模拟来验证理论分析结果。 我们选取一个有n=2 000个节点的无标度网络,其度分布为pk=k-2.7[5-7]。 接触意识函数为ψk=k-0.5,令恢复率γ=1,α1=1. 我们对(11)式进行数值模拟。 为了验证三种意识对传染病阈值的影响,我们分析这三种意识对应参数a,b,μ取不同值时疾病的爆发情况。

图1中我们模拟局部意识对阈值的影响。假设初始阶段染病者的密度为0.1,令b=1/2,可以看出当传播率达到0.58时,疾病爆发,所以阈值β0=0.58.图2中改变参数a的值,β0以0.01的步长从0到1变化。利用(11)式求解得一段时间后染病者的密度ρ. 我们认为ρ>0.002时疾病爆发。取这个β0的值作为传染病阈值并在图中描点。同时绘制了(13)式的图像。显然利用稳定性理论求解的阈值,和数值模拟求解的阈值相差不大。随着局部意识的增强(a增大)传染病阈值也增大。

Fig.1 Dynamic of infection density图1 染病者密度随时间的变化

Fig.2 Influence of local awareness on threshold图2 局部意识对阈值的影响

图3图4中我们分别模拟了局部意识和接触意识对流行病阈值的影响,这个结果与文献[4]一致。

Fig.3 Influence of global awareness on threshold图3 全局意识对阈值的影响

Fig.4 Influence of contact awareness on threshold图4 接触意识对阈值的影响

4 结论

本文建立了简单的SIS传染病模型来研究三种意识对于传染病阈值的影响。 利用平均场模型和稳定性理论求解传染病阈值和基本再生数。 结果表明,局部意识和接触意识可以提高传染病的阈值,但是全局意识不可以。 最后利用数值模拟检验了理论分析的结果。

[1] 靳祯,孙桂全,刘茂省.网络传染病动力学建模与分析[M].北京:科学出版社,2014.

[2] Kiss L Z,Cassell J,Reca M,etal.The Impact of Information Transmission on Epidemic Outbreaks[J].Math:Biosci,2010,225:1-10.DOI：10.1016/j.mbs.2009.11.009.

[3] Wu Q,Fu X,Small M,etal.The Impact of Awareness on Epidemic Spreading in Networks[J].Chaos:AnInterdisciplinaryJournalofNonlinearScience,2012,22:013101.DOI:10.1063/13673573.

[4] Shang Y.Modeling Epidemic Spread with Awareness and Heterogeneous Transmission Rates in Networks[J].BiolPhys,2003,39:489-500.DOI:10.1007/s10867-013-9318-8.

[5] Barabási A L.Scale-free Networks:A Decade and Beyond[J].Science,2009,325:412-413.DOI:10.1126/science.1173299.

[6] Pastor-Satorras R,Vespignani A.Epidemic Spreading in Scale-free Networks[J].PhysicalReviewLetters,2001,86:3200.DOI:10.1103/PhysRevLett.86.3200.

[7] Barabasi A L,Albert R.Emergence of Scaling in Random Networks[J].Science,1999,286(5439)：509-512.DOI:10.1126/Science.286.5439.509.

Stability of SIS Model Based on Awareness in Complex Networks

ZHAO Aimin,TAO Jiaqi,LIU Guirong

(School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China)

We study the influence of three kinds of awareness on the disease transmission,and establish the SIS model on scale-free network,and obtain the epidemic threshold and stability of the disease-free equilibrium point. The results show that both local and contact awareness can raise the epidemic thresholds while the global awareness cannot. Finally,the numerical results are used to verify the theoretical results.

complex network;SIS model;awareness;threshold

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.03.005

2017-06-18；

2017-06-26

国家自然科学基金(11471197)

赵爱民(1963-)，男，博士，教授，主要从事微分方程定性研究。E-mail:zhaoam@sxu.edu.cn

O193

A

0253-2395(2017)03-0421-05