过盈配合拆解的界面损伤及其预测模型研究

沈 健, 黄盼龙, 周 丹, 刘光复, 杜晓东

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 材料科学与工程学院,安徽 合肥 230009)

过盈配合拆解的界面损伤及其预测模型研究

沈 健1, 黄盼龙1, 周 丹1, 刘光复1, 杜晓东2

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 材料科学与工程学院,安徽 合肥 230009)

在机械装备中经常使用过盈配合,过盈配合拆解的难度大,再制造拆解时常常会造成配合界面损伤而导致零件无法再制造。文章针对过盈配合拆解的界面损伤,设计了过盈配合拆解的模拟试验,阐述了试验原理和过程;根据试验结果,分析界面损伤的形式和产生损伤的机理,确定了界面损伤定量表征参数为拆解界面损伤深度;研究了过盈量、材料类型与界面损伤的关系;对Archard模型进行修正,结合试验数据,建立了界面损伤预测模型。

再制造;过盈配合拆解;拆解试验;界面损伤

再制造拆解是再制造的前提,为获得再制造毛坯,需要对机械装备进行拆解,解除零件间的约束[1]。在各种约束类型中,过盈配合使用普遍。对过盈配合件进行拆解时,常常会造成零件配合面的界面损伤,使零件无法再制造。

国内外学者对界面损伤进行了较为广泛的研究。文献[2-3]应用内聚力模型对复合材料界面损伤的形式和机理进行了研究,分析了在载荷作用下界面裂纹的产生过程和扩展;文献[4-5]对钢板板料冲压过程中产生的表面损伤进行了研究,认为表面产生的损伤是板料与模具接触过程中犁沟效应、黏着效应和疲劳效应3种接触效应混合作用的产物;文献[6-7]对轮轨接触表面的接触疲劳损伤进行了研究,认为损伤有剥离、压溃、擦伤、断裂等多种形式。1953年,Archard提出了黏着磨损模型[8],对磨损体积进行了定量计算,并得到了推广;文献[9]用Archard模型预测了模具表面磨损,根据磨损量与磨损系数、压力、相对移动量、硬度之间的关系建立了新的损伤预测模型;文献[10]在研究重载铁路货车车轮磨耗时,运用Archard磨损模型,计算了2种不同轴重的重车车轮在不同工况下的磨耗量。Archard模型在理论推导时作了一些假设,实际运用时需要根据使用条件对模型进行一定的修正。

目前,对于过盈配合拆解造成零件界面损伤的研究很少,对界面损伤产生机理及损伤预测进行研究,以降低拆解的界面损伤具有重要的现实意义。本文以采用过盈配合的大型离心式压缩机的叶轮和主轴为主要研究载体,简化拆解模型,用配对试件来模拟过盈配合拆解过程,分析拆解界面损伤形式、机理和规律,确定界面损伤定量表征参数,建立界面损伤预测模型,为再制造拆解工艺和修复工艺提供一定的理论支持。

1 试 验

1.1 试验设计

1.1.1 试验目的

用配对试件的相对滑动来模拟过盈配合的叶轮和主轴的拆解过程,通过试验分析过盈量、材料类型与拆解界面损伤的关系,研究界面损伤规律,建立损伤预测模型。

1.1.2 试验原理

本文以沈鼓集团的大型离心式压缩机的过盈配合叶轮和主轴为研究对象,叶轮和主轴过盈配合模型如图1所示,该模型轴径为225 mm,过盈量为轴径的1.7‰～2.2‰,过盈配合的过盈量在配合面产生相应的接触压力。

图1 叶轮和主轴过盈配合模型

将过盈配合的叶轮和主轴模型进行简化:接触表面沿圆周方向可以近似为由无数个近似长方体的体积微元组成,体积微元间的接触压力可以看作沿接触面法线方向(即径向)的相互作用力,如图2a和图2b所示。将体积微元抽象提取,接触面的相互作用力通过施加载荷模拟,建立过盈配合配对试件模型,如图2c所示。配对试件受载荷作用,处于三向应力状态[11],与叶轮和主轴过盈配合模型的应力状态类似。

图2 过盈配合体积微元和配对试件模型

配对试件模型用上试件和下试件分别代表过盈配合中的叶轮和主轴,过盈量以过盈量产生的相应接触压力来替代,接触压力通过施加载荷来实现。图2c中,F2为模拟配合界面的接触压力;F1为模拟拆解过程中的拆解力;F3与F1方向相反。保证上试件稳定不动,下试件放在滚动导轨上。根据配对试件模型搭建拆解模拟试验台,如图3所示,法向载荷最大设计值为10.0 t,横向载荷最大设计值为6.4 t。

图3 模拟拆解试验台

接触压力从压缩机叶轮和主轴过盈配合模型的有限元计算中获取,叶轮和主轴在最大过盈量为轴径φ225 mm的2.2‰(即过盈量为0.495 mm)时,配合界面的最大接触压力约为253.27 MPa[12]。

为了模拟不同过盈量下叶轮和主轴拆解造成的损伤,试验时只需设置接触压力小于300 MPa。如果配对试件名义接触面积为10 mm×10 mm,那么300 MPa的接触压力需要施加3.0 t的载荷,试验时施加载荷设置在0～3.0 t之间。

1.1.3 试验过程

(1) 用3.0 t载荷对安装试件进行预压,目的是使试验状况符合实际过盈配合拆解前的状态。

(2) 模拟拆解过程。首先对上试件施加载荷F2,达到设定值后保持不变,再对下试件施加一定大小横向载荷F1,保证下试件能沿水平方向从一端移动到另一端,移动距离为26 mm。

(3) 加载的载荷设置为0～3.0 t,每0.5 t一档,每种载荷做3组试验。

1.2 试样及预处理

1.2.1 试件材料

试件材料及材料特性见表1所列。

表1 试件材料特性

1.2.2 预处理

为了减少拆解因素对拆解界面损伤的影响,对试件都做了相同处理。试件同批次加工,在加工时最后一道工序为磨削,要求表面粗糙度达到0.8 μm;试验前对试件表面用丙酮进行清洗并晾干;由于试件加工时表面会有机加工纹路,试验时保证配对试件界面接触纹路形态相同。

2 界面损伤分析

2.1 界面损伤机理

3种配对材料,共进行54组拆解模拟试验,在试件的表面造成了不同程度的拆解损伤。这些拆解损伤与传统的摩擦磨损实验形成的黏着磨损、磨粒磨损、疲劳磨损以及腐蚀磨损[13]的损伤有显著区别,属于界面间单次单向滑动造成的一种损伤,表现为宏观上的损伤。

配对材料为KMN低强度时不同载荷下的界面损伤形式如图4所示。

由图4可知,从宏观上看,试件界面损伤有多种形式,随着法向载荷的增大,损伤的形式主要表现为划横、犁沟和黏着剥离以及堆积,且随着载荷的增大,界面损伤加重;下试件的界面损伤形式比上试件的明显,但上试件的界面损伤要比下试件的严重。

图4 配对材料为KMN低强度时不同载荷下的界面损伤形式

不同界面损伤形式下的扫描电子显微镜(SEM)放大400倍照片如图5所示。由图5可知,从微观上看,宏观上看到的划横、犁沟和剥离都是黏着损伤,黏着是产生这些形式损伤的主要原因。

图5 配对材料为KMN低强度时不同损伤形式下的SEM图

2.2 界面损伤评价参数及测量

从试件界面损伤形式分析,划横、犁沟和剥离都可以表现为表面材料缺失,损伤深度可以直观地反映界面损伤程度。从再制造修复工艺分析,对于界面损伤,先对损伤区域用电刷镀、热喷涂或激光熔覆等技术进行修复处理,再进行机加工,损伤深度对再制造修复工艺的选择有借鉴作用。因此,用拆解界面损伤深度对试件界面损伤进行评价具有合理性。

采用瑞士Trimos微观形貌及粗糙度测量仪进行测量,其测量深度范围为0～1 100 μm,精度为0.1 μm。测量时选取试件表面损伤最严重的区域,选取的面积为8.0 mm×0.5 mm,以试件原始未损伤表面为起始测量点进行测量,选取测量结果中的三维形貌参数的表面最大高度Sz作为拆解界面损伤深度,如图6所示。通过测量发现,下试件、上试件的拆解界面损伤深度随着载荷的变化有相似的变化趋势,再考虑到下试件的面积大,损伤形式明显,易于测量,本文以下试件作为评价对象,下试件材料为40CrNiMo7。对54组下试件的界面损伤进行测量,结果见表2所列。

图6 下试件表面三维形貌

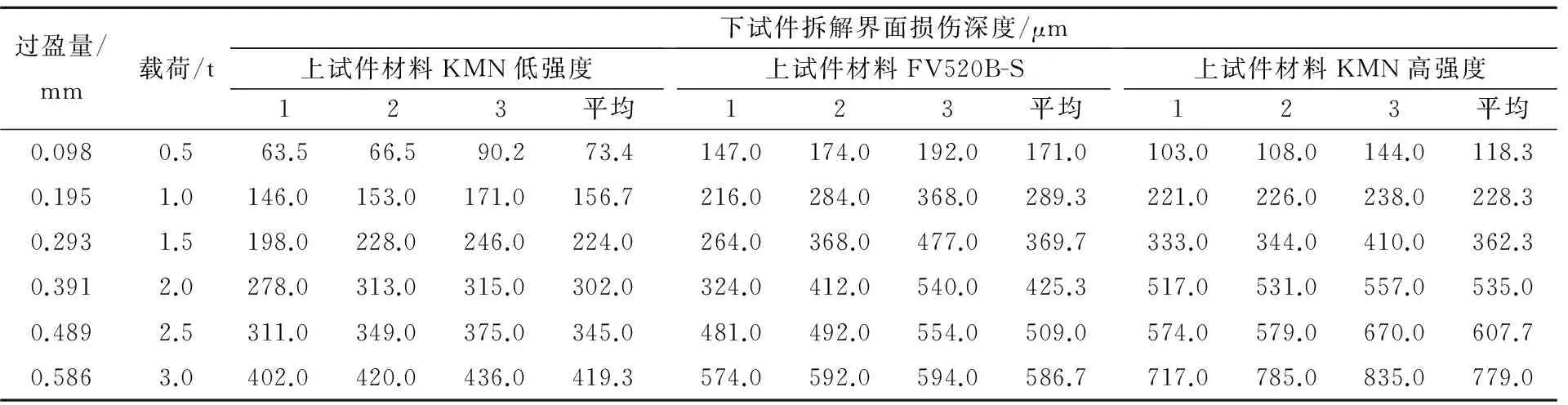
过盈量/mm载荷/t下试件拆解界面损伤深度/μm上试件材料KMN低强度123平均上试件材料FV520B-S123平均上试件材料KMN高强度123平均0.0980.563.566.590.273.4147.0174.0192.0171.0103.0108.0144.0118.30.1951.0146.0153.0171.0156.7216.0284.0368.0289.3221.0226.0238.0228.30.2931.5198.0228.0246.0224.0264.0368.0477.0369.7333.0344.0410.0362.30.3912.0278.0313.0315.0302.0324.0412.0540.0425.3517.0531.0557.0535.00.4892.5311.0349.0375.0345.0481.0492.0554.0509.0574.0579.0670.0607.70.5863.0402.0420.0436.0419.3574.0592.0594.0586.7717.0785.0835.0779.0

2.3 界面损伤规律分析

由于试验过程存在误差,同一种载荷下多次试验的试件界面损伤程度略有不同,拆解界面损伤深度值有一定的波动。为了更好地研究试验规律,定量评价界面损伤,先对测量值用格罗布斯检验法和狄克松检验法[14]进行异常数据处理,排除粗大误差数据,再将相同载荷下的拆解界面损伤深度值做均化处理。通过格罗布斯检验法和狄克松检验法检验,测量数据没有异常值。

根据表2可以得到3种配对材料平均拆解界面损伤深度变化曲线图,如图7所示。从图7可以看出,平均拆解界面损伤深度都随着载荷的增大而增大,且都呈现近似线性关系;在相同载荷下,配对材料为KMN低强度时平均拆解界面损伤深度最小。

根据经典的黏着损伤理论[14]可知,表面损伤与屈服极限有关,可以得到不同载荷下3种上试件材料屈服极限的平均拆解界面损伤深度,如图8所示。

从图8可以看出,3种上试件材料的屈服极限在不同载荷下的平均拆解界面损伤深度呈现2种变化趋势,0.5、1.0、1.5 t 3种载荷下,平均拆解界面损伤深度随屈服极限的增大先增大后减小,配对材料为FV520B-S的平均拆解界面损伤深度最大;2.0、2.5、3.0 t 3种载荷下,平均拆解界面损伤深度随屈服极限的增大而增大。

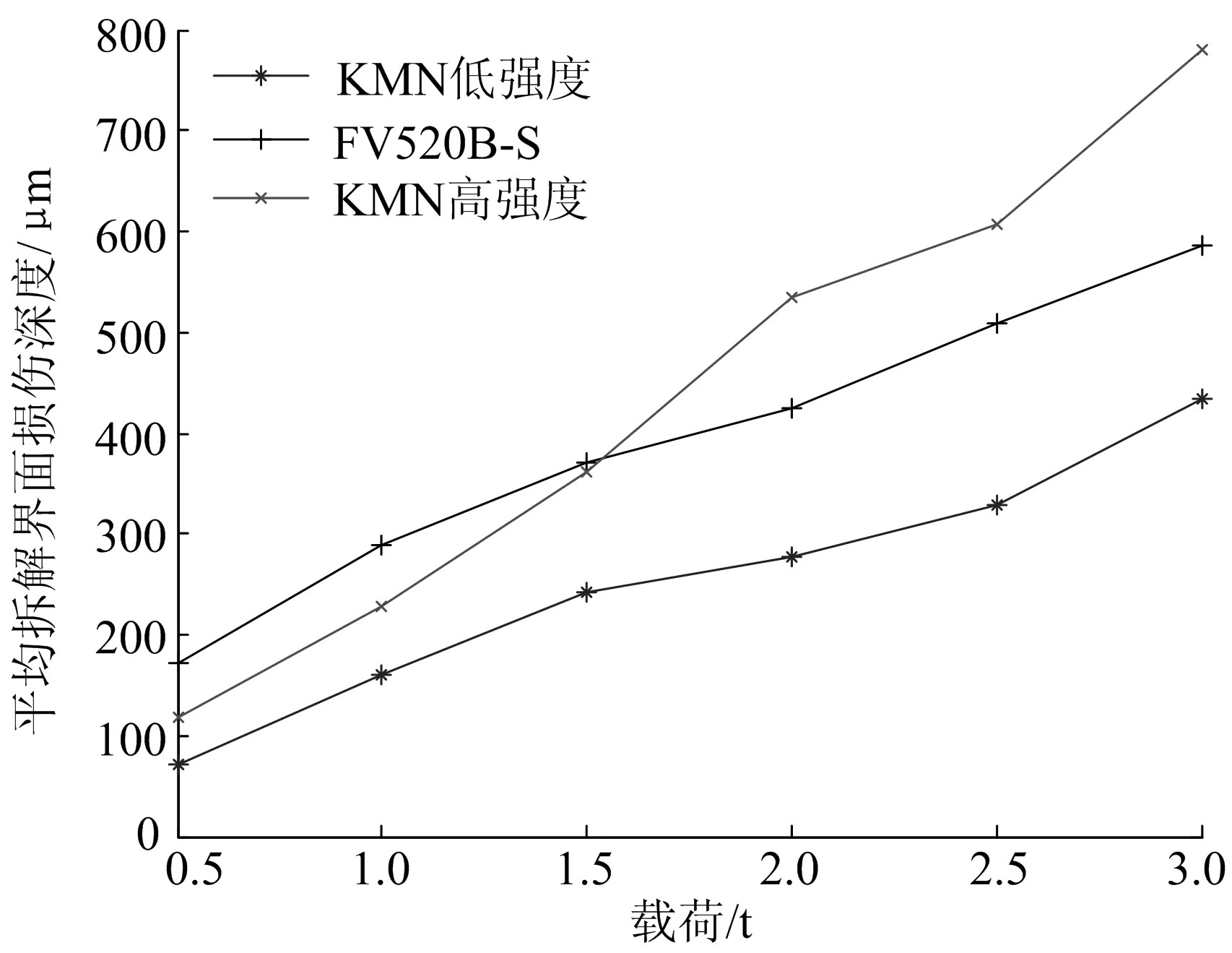
图7 3种材料的平均拆解界面损伤深度变化曲线

图8 不同载荷下3种材料屈服极限的平均拆解界面损伤深度

3 界面损伤预测模型的建立

3.1 黏着磨损的Archard模型

Archard提出了黏着磨损的Archard模型[15]，即

(1)

其中,υ为磨损体积;W为载荷;H为磨损表面的硬度或屈服极限;x为滑动距离;k为取决于接触材料及清洁度的磨损系数。

为了计算磨损深度的变化率,(1)式被改写为[15]:

(2)

3.2 损伤预测模型的建立

对黏着磨损的Archard模型进行变换,即

(3)

则有:

(4)

在试验中推动下试件为匀速过程,令x=vt,则

(5)

记f(k,x,Am)=kx/Am,则

(6)

试验时,滑动距离x=26 mm,名义接触面积Am=10×10=100 mm2,均为定值,因此将f(k,x,Am)定义为拆解损伤系数K,则

d=KW/H

(7)

其中,d为拆解界面损伤深度。

根据2.3节的分析,对推导模型进行修正和分段处理。当载荷为0.5、1.0、1.5 t时,将(7)式修正为:

(8)

当载荷为2.0、2.5、3.0 t时,将(7)式修正为:

(9)

其中,a为待定系数;b为常数;H为配对的上试件材料屈服极限。

为了验证预测模型的可靠性,对3种配对材料分别在0.75、1.25、1.75、2.25、2.75 t载荷下进行拆解模拟试验。将预测模型得到的拆解界面损伤深度与试验得到的拆解界面损伤深度进行比较,结果见表3所列。从表3可以看出,试验的拆解界面损伤深度与预测模型计算的拆解界面损伤深度的相对误差较小,误差一般小于10%。结果出现误差主要是由在试件安装时有一定的安装误差、每组配对试件接触界面的微观接触形态不同等不定因素引起的。

表3 拆解界面损伤预测模型的验证

4 结 论

(1) 本文用配对试件来模拟过盈配合的叶轮和主轴的拆解过程,将过盈配合的过盈量转化为载荷进行试验,研究不同过盈量下过盈配合拆解造成的界面损伤,具有一定的现实意义。

(2) 拆解界面有多种损伤形式,随着法向载荷的增大,损伤的形式主要表现为划横、犁沟和黏着剥离及堆积,黏着是产生这些损伤形式的主要原因。

(3) 以拆解界面损伤深度为界面损伤定量表征参数,针对3种材料配对进行试验研究,发现平均拆解界面损伤深度都随着载荷的增大而增大,且呈现近似线性关系;在相同载荷下,配对材料为KMN低强度时平均拆解界面损伤深度最小。

(4) 建立了拆解界面损伤预测模型并进行了试验验证。

[1] 沈健,郭长福,周丹,等.大过盈配合的叶轮-主轴温差拆解机理的研究[J].合肥工业大学学报(自然科学版),2015,38(1):7-10.

[2] CHANDRA N,LI H,SHET C,et al.Some issues in the application of cohesive zone models for metal-ceramic interfaces[J].International Journal of Solids and Structures,2002,39(10):2827-2855.

[3] KUSHCH V I,SHMEGERA S V,BRONDSTED P,et al.Numerical simulation of progressive debonding in fiber reinforced composite under transverse loading[J].International Journal of Engineering Science,2011,49(1):17-29.

[4] PODGORNIK B,HOG MARK S,PEZDIRNIK J.Comparison between different test methods for evaluation of galling properties of surface engineered tool surfaces[J].Wear,2004,257(7):843-851.

[5] PEREIRA M P,YAN W,ROLFE B F.Contact pressure evolution and its relation to wear in sheet metal forming[J].Wear,2008,265(11/12):1687-1699.

[6] SHUR E A,BYCHKOVA N Y,TRUSHEVSKY S M.Physical metallurgy aspects of rolling contact fatigue of rail steels[J].Wear,2005,258(7):1165-1171.

[7] JIN Y,ISHIDA M,NAMURA A.Experimental simulation and prediction of wear of wheel flange and rail gauge corner[J].Wear,2011,271(1):259-267.

[8] ARCHARD J F.Contact and rubbing of flat surfaces[J].Journal of Applied Physics,1953,24(8):981-988.

[9] 侯英岢.汽车钢板冲压成形表面损伤规律与控制方法研究[D].上海:上海交通大学,2009.

[10] 邵朋朋,傅茂海,周元,等.基于Archard模型的重载铁 路货车车轮磨耗研究[J].铁道机车车辆,2012,32(2):42-45.

[11] 杨伯源.材料力学[M].北京:机械工业出版社,2002:138-142.

[12] 张小敏.压缩机叶轮和轴过盈配合拆解的界面研究[D].合肥:合肥工业大学,2013.

[13] 温诗铸,黄平.摩擦学原理[M].4版.北京:清华大学出版社,2012:171-186.

[14] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2010:47-51.

[15] BHUSHAN B.摩擦学导论[M].葛世荣,译.北京:机械工业出版社,2006:183-189.

(责任编辑 胡亚敏)

Study of interface damage of interference fit dismantling and its prediction model

SHEN Jian1, HUANG Panlong1, ZHOU Dan1, LIU Guangfu1, DU Xiaodong2

(1.School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China; 2.School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

In machinery equipment, interference fit is widely used. It is difficult for interference fit dismantling. Remanufacturing dismantling often damages the interface which means that parts can not be remanufactured. To research the interface damage of interference fit dismantling, the simulation test of interference fit dismantling is designed, and its principle and process are introduced. Based on the test results, the form and the mechanism of interface damage are analyzed, and the quantitative parameter for the characterization of interface damage is confirmed as dismantling interface damage depth. The relation among the magnitude of interference, the type of material and interface damage is explored. With Archard model corrected and combining with experimental data, the prediction model of interface damage is established.

remanufacturing; interference fit dismantling; dismantling test; interface damage

2016-02-19；

2016-04-21

国家重点基础研究发展计划(973)资助项目(2011CB013400);国家自然科学基金青年科学基金资助项目(51405121)

沈 健(1956-),男,江苏溧阳人,博士,合肥工业大学教授,硕士生导师; 刘光复(1945-),男,辽宁开源人,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.08.002

TH17

A

1003-5060(2017)08-1014-06