基于模糊控制的三轮全转向叉车转向研究

陈 明, 肖本贤

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

基于模糊控制的三轮全转向叉车转向研究

陈 明, 肖本贤

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

目前对三轮全转向叉车的研究一般集中在研究车辆模型,但缺乏考虑转向规律是否符合阿克曼转向定理,也缺乏对各类工况下的叉车转向分析,尤其是负载情况下的叉车转向分析。文章以车辆的二自由度线性模型为基础进行展开研究。整车系统仿真的输入为方向盘转角,模糊控制器以质心侧偏角等于0为控制目标来控制后轮转角,同时用阿克曼转向定理来调整左前轮和右前轮转角,由此实现三轮全转向。最后通过对各种转向工况下的仿真,验证了模糊控制转向策略的有效性。

叉车;三轮全转向;阿克曼定理;模糊控制;负载

0 引 言

目前国内对车辆的转向研究主要停留在建立车辆模型,选择各种控制策略。但很少针对一些特殊的叉车进行建模,即使针对叉车建模,也只考虑到空载时的叉车转向。叉车主要应用于工业中的货物搬运,在大多数情况下都是负载工作,而且转向频繁,因此叉车对转向稳定性要求较高。国内缺乏对这种叉车负载情况下转向的具体研究,文献[1]提出的转向控制策略没有在负载时保证叉车转向稳定性;文献[2-3]提出的横摆角速度反馈控制策略没有考虑转向规律符合阿克曼转向定理,这会导致转向时车轮产生侧滑,增大行驶阻力,增加轮胎磨损。

本文在车辆二自由度线性模型的基础上,同时满足阿克曼转向定理,根据TFC20全向前移式电动叉车建立了三轮全转向叉车转向模型,并基于质心侧偏角等于0的目标利用模糊控制转向策略在各种条件下对其进行仿真,验证了模型的正确性和控制策略的有效性。

1 建立三轮全转向叉车转向模型

1.1 三轮全转向叉车转向模型

为了转弯时车轮做纯滚动无滑移运动,必须满足阿克曼定理,叉车转向中心必须交于一点,如图1所示。图1中,Ο′为叉车转向中心,与前轴的距离为e,与后轴的距离为f;质心Ο与前轴距离为a,与后轴距离为b;δ1为左前轮转角;δ2为右前轮转角;δ3为后轮转角;c为左前轮和右前轮中心的距离;L为前轮中心到后轮中心的距离。

图1 三轮全转向叉车转向模型

为了满足阿克曼定理,转向中心交于O′,3个轮子转角必须符合如下关系:

(1)

假设方向盘给定转角为δ,后轮转角δ3与方向盘给定转角δ成k的比例关系,并且方向相反,根据阿克曼定理推导得到3个轮子转向角如下:

(2)

1.2 建立二自由度线性动力学方程

建立三轮全转向汽车二自由度线性动力学系统模型[4-5],由于车辆行驶过程非常复杂,在简化模型时必须保证行驶过程真实性,故需做如下假设:

综上所述，磁混凝澄清池集混凝、沉淀、过滤功能于一池，因此该池排泥浓度高，有利于污泥的处理。由于该池型沉淀效率高，因而多用于老厂改造挖潜或用地面积较为紧张的水厂及寒冷地区的水厂，适合于室内建设。

(1) 不考虑车辆绕x轴方向的侧倾运动,也不考虑绕y轴的俯仰运动,只考虑绕z轴的横摆运动。

(2) 不考虑切向力和空气阻力对车辆影响。

(3) 车辆沿x方向前进时匀速行驶。

动力学模型中的参数如下:Fy1、Fy2、Fy3为3个轮子轮胎侧偏力;δ1、δ2、δ3分别为三轮转角;u、v分别为整车质心处纵向速度与侧向速度;β为质心侧偏角;γ为横摆角速度;m为整车质量;Jz为整车绕z轴转动惯量。建立三轮全转向二自由度线性动力学方程[6]为:

(3)

其中,质心侧偏角可以取近似值β=v/u。由于车轮转角很小(δ1、δ2、δ3小于5°),因此可以近似取值cosδ1(δ2,δ3)=1。由(3)式近似得到:

(4)

实验表明,当侧偏角小于5°时,侧偏力Fy与侧偏角α表现为线性关系。因此本文中三轮全转向叉车选用的轮胎模型保持在线性范围内。选用该线性模型,能够较好地反映轮胎侧偏力与轮胎侧偏角之间的关系,又不会使模型过于复杂化。

该轮胎模型下,3个轮子的侧偏力为:

(5)

其中,α1、α2、α3分别为三轮侧偏角;C1、C2、C3分别为3个轮子的轮胎侧偏刚度。

根据几何关系,3个轮子侧偏角如下:

(6)

将3个轮子的侧偏角带入(5)式,可以得到3个轮子的侧偏力为:

(7)

再把轮胎侧偏力带入二自由度线性动力学方程(4)式,可得:

(8)

最终可得质心侧偏角和横摆角速度的计算公式如下:

(9)

2 三轮全转向模糊控制策略

后轮转角δ3与方向盘转角δ的比例系数k并不应该一成不变,而是随着工作环境的变化而改变,比如叉车车速变化,或者是叉车负载的变化影响。模糊控制理论经常应用于一些复杂可变的被控对象,因此本文采用模糊控制的转向策略。三轮全转向模糊控制策略以质心侧偏角等于0为目标来控制后轮转角δ3与方向盘转角δ的比例系数k,再根据阿克曼定理调整左前轮转角δ1和右前轮转角δ2,实现叉车三轮全转向,达到更稳定的转向效果。

本文采用的二维模糊控制器[7]如图2所示。以质心侧偏角误差E和质心侧偏角误差的导数EC作为输入变量,而输出变量k则是后轮转角和方向盘转角比例系数。输入量化因子为K1、K2,输出比例因子为K3。输入精确量质心侧偏角误差E和误差导数EC被量化后,经过模糊控制决策和推理后送到解模糊化部分,实现模糊量向精确量的转化,输出量经比例因子后得到精确量比例系数k的输出。

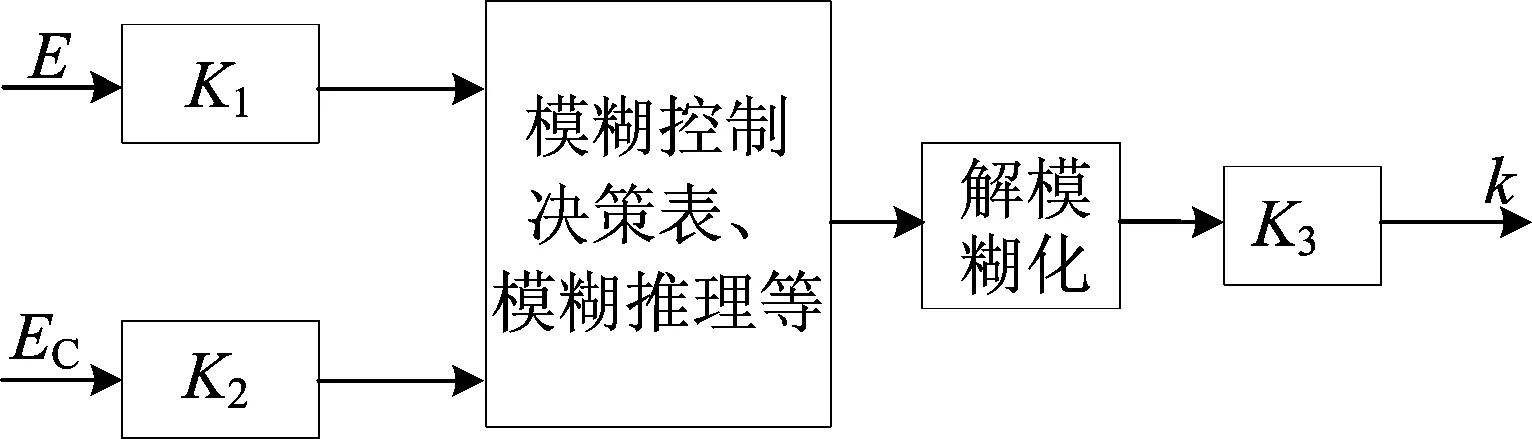
图2 二维模糊控制器结构

根据实际经验,模糊控制系统中论域选择如下:质心侧偏角误差E的论域范围选为[-6,6];质心侧偏角误差导数EC论域范围选为[-6,6];后轮转角和方向盘转角比例系数论域范围选为[-1,1]。隶属度函数选为三角形函数。E、EC、U的模糊集选为{NB,NM,NS,ZO,PS,PM,PB},具体如下:E={NB,NM,NS,ZO,PS,PM,PB},对应的语言值为{-6,-4,-2,0,2,4,6};EC={NB,NM,NS,ZO,PS,PM,PB},对应的语言值为{-6,-4,-2,0,2,4,6};U={NB,NM,NS,ZO,PS,PM,PB},对应的语言值为{-1,-0.7,-0.3,0.1,0.4,0.7,1}。

模糊控制器2个输入变量的语言值都为7,则总共有49条if A and B then C的规则,见表1所列。

表1 模糊控制规则

在下文中,本模糊控制转向策略将和后轮固定比例转向策略以及传统单后轮转向策略相比较来验证其有效性。其中传统单后轮控制转向是指左前轮和右前轮转角为0,后轮转角和方向盘转角相同的控制方法。后轮固定比例转向是指后轮转角与方向盘转角比例系数k固定为0.5,然后根据阿克曼转向定理调整左前轮和右前轮转角的控制方法。

3 仿真实验结果及分析

为了验证上文提出的模糊控制转向策略的有效性,基于Matlab 进行了SIMULINK仿真[8-9]。本文根据TFC20全向前移式电动叉车的实际数据进行计算和分析。整车自重m=5 000 kg,空载情况下叉车质心到前轴距离a=1.408 m,质心到后轴距离b=0.512 m,叉车前后轴的距离L=1.92 m,两前轮之间的距离c=1.88 m,左前轮、右前轮和后轮的轮胎侧偏刚度C1、C2、C3分别为77 850、77 850、153 840 N/rad,横摆惯量Jz=5 000 kg·m2。

3.1 空载情况下叉车转向

首先仿真叉车在空载情况下,速度选择中速10 km/h,方向盘转角选择输入初始值为0,斜率为 0.16 rad/s,经过 1 s 后达到 0.16 rad,然后保持不变。仿真得到的质心侧偏角、横摆角速度和3个轮子转角分别如图3所示。从图3a可以看出,模糊控制转向的质心侧偏角明显比其他2种控制策略要小,经过1.5 s后保持在-0.021 rad,而后轮固定比例转向的质心侧偏角保持在-0.036 rad左右,达到稳定的时间1.8 s稍长。传统单后轮转向质心侧偏角最大,达到了-0.131 rad。从图3b可以看出,后轮固定比例转向横摆角速度最大达到0.372 rad/s,传统单后轮转向稳定在0.247 rad/s,模糊控制转向横摆角速度减小,经过1.4 s后保持在0.213 rad,既不会过度转向产生甩尾,也不会出现转向不足。而传统单后轮转向质心侧偏角过大,后轮固定比例转向横摆角速度过大,而模糊控制转向策略转向的稳定性更好。

由于传统单后轮控制转向的三轮转角较明显,左前轮和右前轮转角都为0,后轮转角和方向盘转角一样,图3c中只给出了后轮固定比例控制转向和模糊控制转向2种方法的三轮转角,固定比例转向时左前轮转角为0.180 rad,模糊控制转向时转角减小到0.099 rad。固定比例转向时右前轮转角为0.142 rad,模糊控制转向时转角减小到0.086 rad,固定比例转向时后轮转角为-0.080 rad,模糊控制转向时转角减小到-0.046 rad。由此可得模糊控制转向时三轮转角有一定减小,在短时间能够达到稳定,实现三轮全转向。

再进行一次高速大角度转向工况下的仿真实验,结果如图4所示,叉车速度增大为15 km/h,给定方向盘转角选择相对较大,选择输入初始值为 0,斜率为 0.3 rad/s,经过 1 s 后达到 0.3 rad,然后保持不变。从图4a可以看出,质心侧偏角明显比方向盘转角为0.16 rad时大,传统单后轮转向质心侧偏角最大,在1.5 s时趋向于稳定达到-0.246 rad,固定比例转向质心侧偏角在相同时间,最后稳定在-0.067 rad,而模糊控制转向的质心侧偏角最小,稳定在-0.042 rad左右,在3种转向策略中最稳定,总体来说所有策略质心侧偏角都比中速小转角工况时要大。

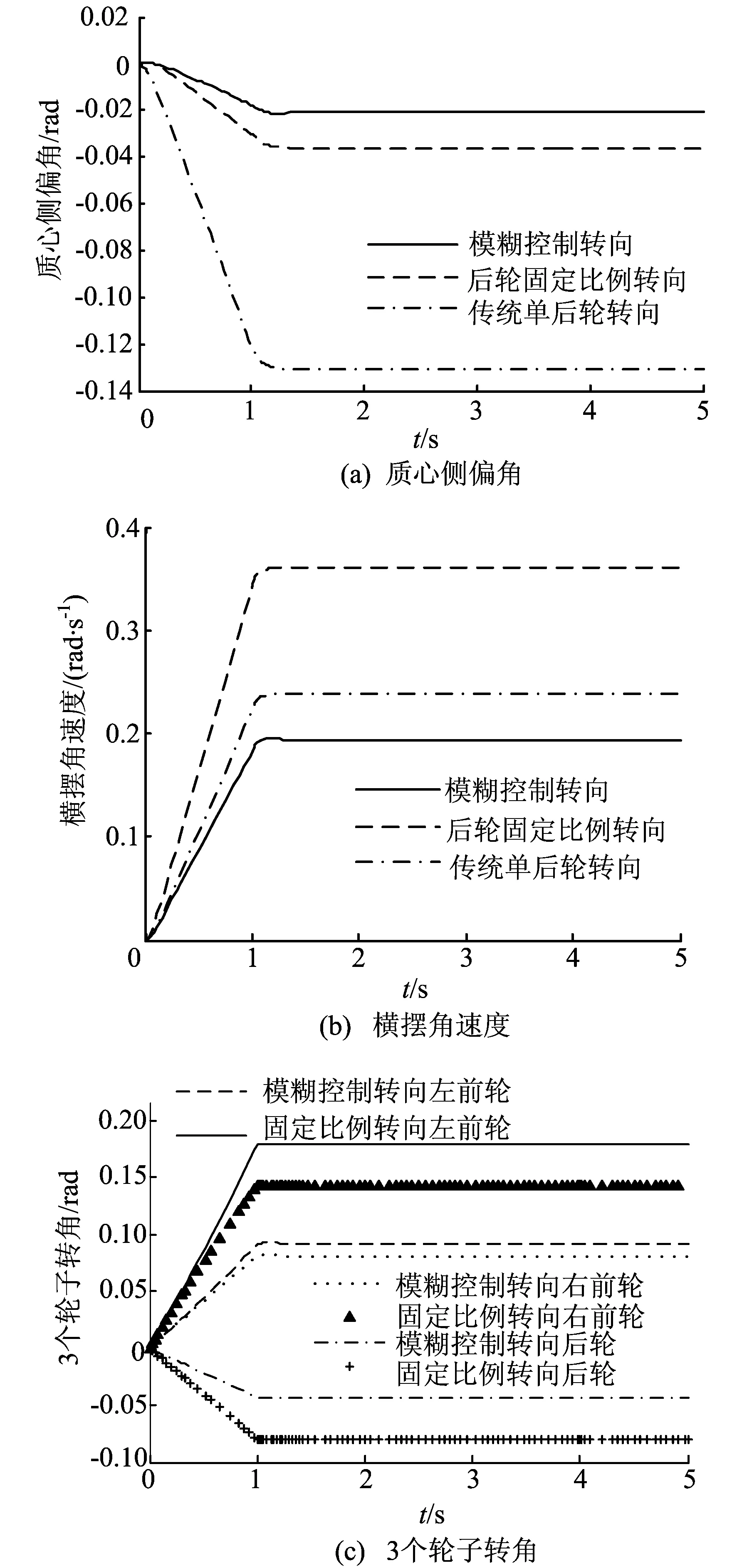
图3 中速小转角工况

图4b中后轮固定比例转向的横摆角速度上升到0.704 rad/s左右保持不变,传统单后轮转向的横摆角速度上升到0.462 rad/s左右保持稳定,而模糊控制转向的横摆角速度最小,上升到0.432 rad/s左右保持不变,相比中速小角度转向工况比较大,符合实际情况。传统单后轮转向和模糊控制转向的横摆角速度虽然相差不大但都比较小,可是质心侧偏角明显过大,转向不够稳定。后轮固定比例转向虽然质心侧偏角只是稍大,但是横摆角速速度过大,容易导致过度转向产生甩尾现象,转向不够稳定,而模糊控制转向则是最优的转向策略。

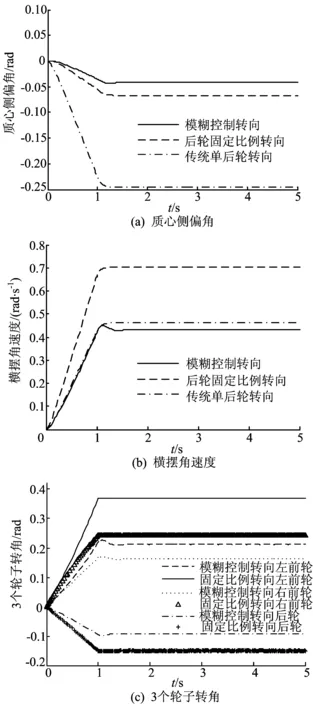
图4 高速大转角工况

同样图4c中只显示后轮固定比例转向和模糊控制转向2种策略叉车3个轮子的转角变化情况,固定比例转向时左前轮转角为0.370 rad,模糊控制转向时转角减小到0.212 rad。固定比例转向时右前轮转角为0.242 rad,模糊控制转向时转角减小到0.162 rad,固定比例转向时后轮转角为-0.150 rad,模糊控制转向时转角减小到-0.093 rad。由此可得模糊控制转向时叉车3个轮子的转角都有一定减小,而且与中速小角度转向工况下的三轮转角都不相同。

3.2 负载情况下叉车转向

因为实际工作中,在大多数情况下叉车都是负载行驶的,所以选择对在额定负载情况下的叉车转向进行进一步分析[10]。负载情况下叉车质心位置发生了偏移,叉车质心位置计算公式如下:

(10)

其中,G0为整车自重;Gp为额定负载质量;Ga为额定负载时叉车总重;a0为叉车空载时质心到前轴的距离;ap为重物的质心到前轴的距离;a为叉车额定负载时质心到前轴的距离。

本文的研究对象TFC20全向前移式电动叉车额定负载质量Gp=2 000 kg,假定重物重心正好在货叉中间,可以计算得到叉车额定负载时质心到前轴的距离a=1.13 m,则质心到后轮轴的距离b=0.79 m。在这种条件下方向盘转角同样给定输入初始值为 0,斜率为0.16 rad/s,经过 1 s 后达到 0.16 rad,然后保持不变,车速同样定为中速10 km/h进行仿真。额定负载工况如图5所示。

质心侧偏角结果如图5a所示。叉车在额定负载时,后轮固定比例转向质心侧偏角和模糊控制转向时很接近,最后稳定到-4.21×10-3rad,而模糊控制转向时质心侧偏角稳定值下降到了-2.40×10-3rad,稳定时间都在1.4 s左右,传统单后轮转向质心侧偏角最大,稳定值为-0.109 rad/s。叉车在额定负载时进行模糊控制转向,质心侧偏角比空载时更小更接近于0,同时负载对质心侧偏角达到稳定的时间影响也不大,说明叉车在负载情况下转向更稳定。

横摆角速度结果如图5b所示,后轮固定比例转向时横摆角速度达到0.361 rad/s,传统单后轮转向稳定在0.239 rad/s,采用模糊控制转向后减小到0.194 rad/s,相比相同车速和相同方向盘转角时,叉车空载时横摆角速度变化不大,保持良好的转向稳定性。

同样来观察图5c中所示后轮固定比例转向和模糊控制转向时叉车3个轮子的转角变化情况,固定比例转向时左前轮转角为0.180 rad,模糊控制转向时转角减小到0.092 rad。固定比例转向时右前轮转角为0.142 rad,模糊控制转向时转角减小到0.081 rad,固定比例转向时后轮转角为-0.080 rad,模糊控制转向时转角减小到-0.042 rad。由此可得模糊控制转向时叉车3个轮子的转角都有一定幅度的减小。可以看出与相同车速、相同方向盘转角但叉车空载情况时相比,叉车额定负载时采用后轮固定比例转向策略3个轮子的最终转角不变,而采用模糊控制转向策略3个轮子的最终转角有小幅度的改变,转向过程中更适应叉车负载变化,达到更好的转向效果。

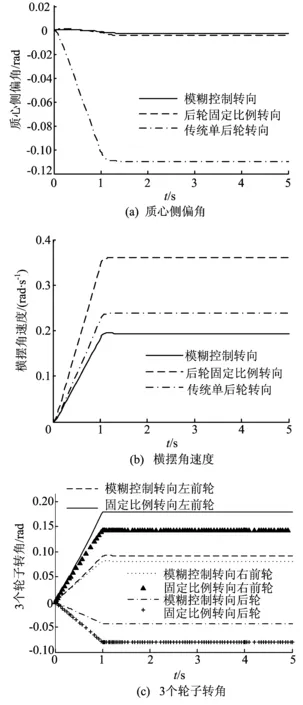
图5 额定负载工况

4 结 论

本文根据三轮全转向叉车的基于阿克曼定理的二自由度模型,对采用模糊控制转向策略的三轮全转向叉车的转向特性进行了理论分析和仿真。仿真结果表明不同车速不同转角情况下,空载和负载情况下三轮全转向模糊控制转向策略都是行之有效的,提高了转向稳定性。

[1] 田承伟,宗长富,何磊,等.汽车线控四轮转向控制策略[J].吉林大学学报(工学版),2010,40(5):1177-1182.

[2] 施国标,余蕾艳,林逸.四轮线控转向横摆角速度反馈控制策略研究[J].系统仿真学报,2008,20(2):506-508.

[4] 徐小东,张冰战.基于模糊逻辑的混合动力汽车控制策略研究[J].合肥工业大学学报(自然科学版),2012,35(6):725-728.

[5] 舒进,陈思忠,杨林.四轮独立转向系统控制策略与试验[J].农业机械学报,2005,36(7):25-31.

[6] 李巾帅.基于多目标优化的四轮独立电动汽车转向控制方法[D].秦皇岛:燕山大学,2013.

[7] 吴佳楠,肖本贤,方兴志,等.基于模糊控制的叉车线控转向系统变传动比研究[J].合肥工业大学学报(自然科学版),2014,37(8):912-915.

[8] 宋宇,陈无畏,陈黎卿.四轮转向车辆横摆角速度反馈与神经网络自适应混合控制的研究[J].汽车工程,2013,35(1):66-71.

[9] 李剑锋,高利,刘碧荣.基于SIMULINK的参数化车辆模型及其实验验证[J].仪器仪表学报,2006,27(6):98-104.

[10] 林程,孟祥,陈思忠,等.四轮转向车辆转向特性分析及试验研究[J].北京理工大学学报,2004,24(3):218-221.

(责任编辑 张 镅)

Research on the steering of three-wheel steering forklift based on fuzzy control

CHEN Ming, XIAO Benxian

(School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China)

At present, the research on three-wheel steering forklift generally concentrates on the vehicle model, ignoring whether the steering law is in accordance with Ackermann steering theorem, and lacking the analysis of the steering performance of forklift under all kinds of working conditions, especially the analysis of the steering performance of forklift under load. This study is based on a 2-DOF linear vehicle model. The steering wheel angle is input to the simulation of vehicle system, and the fuzzy controller controls the angle of rear wheel to make sure that the sideslip angle is equal to zero, and simultaneously adjusts the left front wheel angle and the right front wheel angle according to Ackermann steering theorem, thus realizing the three-wheel independent steering. Finally, the simulation results under different steering conditions show the effectiveness of the presented fuzzy control based steering strategy.

forklift; three-wheel steering; Ackerman steering theorem; fuzzy control; load

2016-01-11；

2016-03-01

国家自然科学基金资助项目(61304007)

陈 明(1992-),男,浙江嵊州人,合肥工业大学硕士生; 肖本贤(1964-),男,安徽无为人,博士,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.08.011

U463.42;TP273.4

A

1003-5060(2017)08-1064-06