Lü系统的全局指数吸引集和正向不变集估计

李慧民, 孙尚庆

(合肥工业大学 数学学院,安徽 合肥 230009)

Lü系统的全局指数吸引集和正向不变集估计

李慧民, 孙尚庆

(合肥工业大学 数学学院,安徽 合肥 230009)

作为一个著名的混沌系统,Lü系统吸引集的精确估计具有重要的理论意义和实际应用。文章利用Lyapunov函数理论,给出了该系统的全局指数吸引集和正向不变集的估计。具体来说,就是将状态空间分成若干区域,在每一个区域上构造恰当的广义正定函数,结合经典技巧获得该估计;最后,通过仿真验证了估计的有效性。

Lü混沌系统;广义Lyapunov函数;全局指数吸引集;正向不变集

0 引 言

自Lorenz系统于1963年被发现以来,许多新混沌系统也相继被发现,其中著名的有Chen系统[1]和Lü系统[2]。作为一个介于Lorenz系统与Chen系统之间的系统,Lü系统一直被广泛而深入地研究[3-7]。

在混沌系统的定性分析中一个非常重要的问题是如何精确地估计其吸引集,这是由于一方面平衡点、周期解、混沌吸引子在全局吸引集中;另一方面在应用中混沌控制、混沌同步也经常需要这些估计。文献[8]首次提出了一个新的概念——全局指数吸引集,且对Lorenz系统族给出这类吸引集的估计。与经典意义下的吸引集[9]相比,全局指数吸引集提供了收敛速度。文献[10]利用多个Lyapunov函数方法构造出了Chen系统的全局指数吸引集与正向不变集。对Lü系统, 其经典吸引集估计由文献[11]给出,但其全局指数吸引集的估计仍然未知。受上述文献启发,本文通过构造3个Lyapunov函数,给出 Lü系统的全局指数吸引集和正向不变集的估计。

1 预备知识

考虑下列的Lü系统:

(1)

其中,a>0;b>0;c>0。令X(t)=(x(t),y(t),z(t))T,X(t0)=X0,X0是(1)式的初值且X=(x,y,z)T为(1)式的状态变量。

定义2[10]对于系统(1),若存在紧集Ω⊂R3,对所有X0=X(t0)∈Ωc,存在常数M(X0)>0、α>0,使得ρ(X(t),Ω)≤M(X(t0))e-α(t-t0),则称系统(1)具有全局指数吸引性,并称Ω是全集指数吸引集。

定义3[10]对于系统(1),若存在一个广义正定的径向无界Lyapunov函数V(x)和L>0、α>0,使得当t≥t0,V(X(t))>L时,不等式V(X(t))-L≤(V(X0)-L)e-α(t-t0)成立,则称系统(1)是全局指数吸引的,Ω={X|V(t)≤L,t≥t0}称为全局指数吸引集。

2 主要定理及证明

引理1 若y(t)具有全局指数吸引集,即存在常数k>0、α>0,使得当t≥t0时,有

则(1)式的一个分解量x(t)亦有全局指数吸引集,且当t≥t0时,有下列估计式:

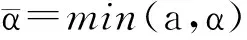
引理2 若x(t)、y(t)均具有全局指数吸引集,即|y(t)|≤k+|y(t0)|e-α(t-t0),|x(t)|≤k+|x(t0)|e-α(t-t0),其中,k≥0、α>0为常数,t≥t0,则z(t)亦有全局指数吸引集,即当t≥t0时,有

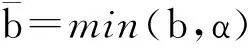
上述2个引理可按文献[10]类似证明。

均为正定矩阵;

均为负定矩阵。

令λM(Qi)、λM(Pi)分别表示Qi、Pi的最大特征值,i=1,2,3,且

在x=0,z≤ξ平面作广义正定Lyapunov函数，即

在(y,z)平面的第一象限内作广义正定径向无界的Lyapunov函数，即

在(y,z)平面的二象限内作广义正定径向无界的Lyapunov函数，即

图1 示意图

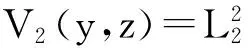
证明 因为系统(1)关于(x,y)的对称性,所以只需考虑x≥0的情况。

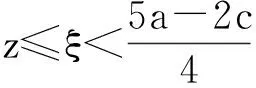
沿系统(1)的解对V1求导数,当z≤ξ时,有

(2)

从(2)式可以看出，

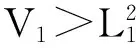
可知Ω为(y,z)的全局指数吸引集和正向不变集。

(3)

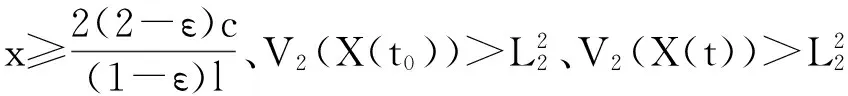
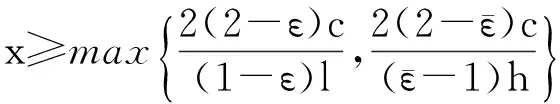
从而有：

即轨线(y(t),z(t))从右往左走的。因为当y≠0时,轨线是指数型衰减,所以由Lefschetz开拓原理知,在y=0上,轨线也是指数型衰减的。证毕。

为(x,y,z)的全局指数吸引集和正向不变集。

3 仿 真

下面对Lü系统中的具体参数进行仿真,以验证方法的有效性。取a=36,b=3,c=20,此时系统处于混沌状态[11],满足定理1和定理2的条件,令ξ=34.5,η=2.5,于是,当|x|≥29 584.8时,有

为(1)式的(y,z)的全局指数吸引集和正向不变集。G={(x,y,z)||x|≤29 584.8}为(x,y,z)的全局指数吸引集和正向不变集。

4 结 论

本文通过构造3个不同的广义正定的Lyapunov函数,并结合经典技巧,给出了Lü系统全局指数吸引集和正向不变集的估计,最后的仿真验证了结论的有效性。

[1] CHEN G R,UTEA T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1465-1466.

[2] LV J H,CHEN G R.A new chaotic attractor coined[J].International Journal of Bifurcation and Chaos,2002,12(3):659-661.

[3] LV J H,CHEN G R,ZHANG S C.Dynamical analysis of a new chaotic attractor[J].International Journal of Bifurcation and Chaos,2002,12(5):1001-1015.

[4] DANCA M F.Synthesizing the Lü attractor by parameter-switching[J].International Journal of Bifurcation and Chaos,2011,21(1):323-331.

[5] CHEN A M,LU J A,LV J H,et al.Generating hyperchaotic Lü attractor via state feedback control[J].Physica A,2006,364:103-110.

[6] SUDHEER K S,SABIR M.Hybrid synchronization of hyperchaotic Lu system[J].Indian Academy of Sciences,2009,73(4):781-786.

[7] RATCHAGIT K,PHAT V N.Stability of Lu’s system[C]//.2010 2nd International Conference on Computer Engineering and Technology.[S.l.]:IEEE,2010:648-651.[8] 廖晓昕,罗海庚,傅予力，等.论Lorenz 系统族的全局指数吸引集和正向不变集[J].中国科学 E辑:信息科学,2007,37(6):757-769.

[9] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001:41-46.

[10] 廖晓昕,徐炳吉,陈关荣，等.Chen混沌系统全局指数吸引集和正向不变集的构造性证明及应用[J].中国科学 E辑:信息科学,2015,45(1):129-144.

[11] ZHANG F C,MU C L,LI X W.On the boundness of some solutions of the Lü system[J].International Journal of Bifurcation and Chaos,2012,22(1):1250015-1-1250015-5.

(责任编辑 朱晓临)

Estimations on globally exponentially attractive set and positive invariant set of Lü system

LI Huimin, SUN Shangqing

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

As a famous chaotic system, accurate estimations for attractive set of Lü system has important theoretical significance and practical applications. In this paper, an estimation on globally exponentially attractive set and positive invariant set of Lü system is given by constructing several generalized positive Lyapunov functions. Specifically, the state space can be divided into several regions, and for each region an appropriate generalized positive definite function is constructed and the estimate is obtained by combining with classical technique. Finally, the validity of the estimates is shown through the simulation.

Lü chaotic system; generalized Lyapunov function; globally exponentially attractive set; positive invariant set

2016-05-13

安徽省高等学校省级自然科学研究重点资助项目(2012AJZR0323)；安徽省省级质量工程专业综合改革试点资助项目(2012zy007)和名师(大师)工作室资助项目(2015msgzs126)

李慧民(1978-),女,河南濮阳人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.08.026

O175.13

A

1003-5060(2017)08-1144-05