矩形水箱保温过程数值模拟与试验研究

唐景春, 孟晓磊, 张 健

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

矩形水箱保温过程数值模拟与试验研究

唐景春1, 孟晓磊1, 张 健2

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

文章对矩形太阳能蓄热水箱在保温过程中的温度场进行了数值计算,并对水箱内部流体出现的温度分层现象进行了试验研究。数值计算和试验结果表明:矩形水箱在蓄热结束后,其内部流体已经形成一定的温度梯度;在38 h试验时间内,水箱中下部温度分层良好,即水箱内部流体各测点温度均没有出现较大的温度波动,基本呈线性下降趋势。壁面的对流换热以及顶部检修口的漏热,是水箱内部流体温度分层现象产生的主要原因。依据试验数据并结合工程实际,该文提出了太阳能蓄热循环温差设置的改进方式。

数值计算;试验;矩形水箱;温度分层;漏热

0 引 言

根据住建部专家统计, 建筑能耗约占全社会总能耗的30%,其中热水供应、采暖约占中国建筑总能耗的25%左右[1]。太阳能跨季节蓄热采暖系统蓄存的热量不仅可用于建筑物采暖、热水供应等,还可应用于电力、制冷、食品等多个行业,该技术的应用可大幅度降低不可再生能源消耗。

以水作为蓄热介质的中低温蓄热技术是太阳能跨季节蓄热采暖的关键技术,水箱作为太阳能跨季节蓄热采暖系统的主要组成部分之一,其性能对系统整体效率有着重要的影响。

目前,已经有许多学者对圆柱形蓄热水箱的工作过程进行了研究分析。文献[2]对分层水箱做了试验研究,研究表明扩散和壁面导热会减弱和破坏水箱分层程度;文献[3]对带有保温层的竖直圆柱形水箱的保温过程进行了数值模拟与试验研究,研究表明圆柱形水箱的保温过程分为非稳态与准稳态2个阶段。然而,当水箱容量超过30 t(低于1 000 t)时,圆柱形水箱的制造、运输成本会大幅上升。

矩形水箱具有强度高、重量轻等优点,在工程中可以根据场地情况现场拼装焊接,比圆柱形水箱有更高的土地利用率。文献[4-5]对卧式热分区水箱储能过程进行了试验研究,讨论了低理查逊数对水箱近壁面扰动的影响,但对其保温过程研究不足。在保温过程中,水箱内部会出现温度分层现象,良好的温度分层不仅可以降低集热器进口温度,提高集热器效率,还能增加可利用的热水量,提高太阳能保证率(solar fraction)[6]。因此,本文采用数值模拟与试验相结合的方法,对矩形水箱保温过程温度分层过程与机理进行了研究。

1 太阳能跨季节储热试验平台

试验平台原理如图1所示。系统由U型管集热器、板式换热器、蓄热水箱、传感器以及其他阀门组件构成。系统循环采用温差控制原理,当太阳能集热器出口处水温与水箱内水温差值达到设定值时,温差循环泵开始工作,从太阳能集热器出来的热水通过板式换热器与蓄热水箱的水进行热量交换,将热量储存在水箱内部。

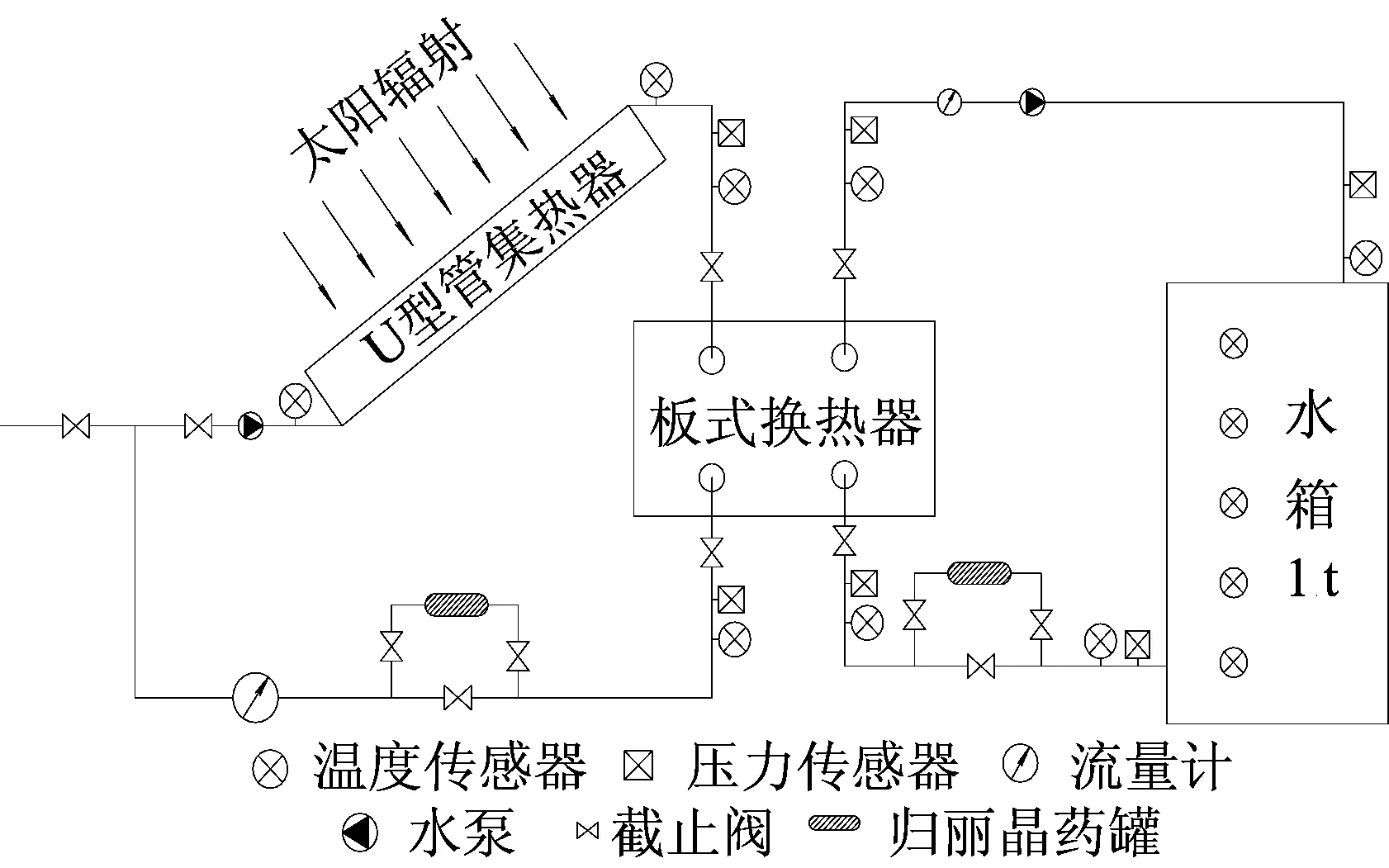
图1 试验平台原理图

储热水箱为矩形,如图2所示。水箱由冲压成形的不锈钢标准板(1 m×1 m,厚0.75 mm)焊接而成,1 m×1 m的单元体上冲有深度为60 mm、半径r为1 084 mm的球冠,水箱顶部预留检修口,直径D=500 mm。水箱各壁面均包裹有硬质聚氨酯保温材料,厚度为50 mm。

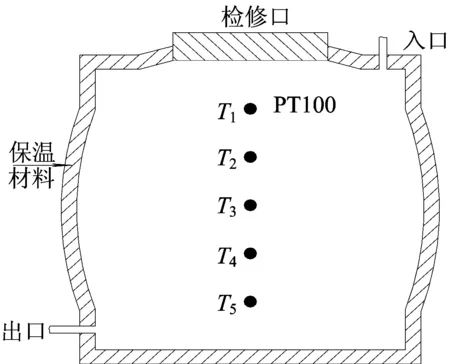
图2 水箱示意图

试验测量了水箱竖直方向温度随时间的变化。在水箱的竖直方向,均匀布置了5个温度变送器(PT100,T1～T5),温度变送器精度为0.2%。试验初始条件如下:① 系统蓄热过程中管道流速为0.814 m/s,蓄热结束后,5个测点(自上而下)的水温分别为322.702、323.279、323.924、322.256、321.806 K;② 室温为289.15 K;③ 试验持续时长为38 h。试验期间,温差换热循环装置关闭,水箱与集热器没有热量交换。

2 数学模型与边界条件

当水温高于4 ℃时，水的密度随水温的升高而减小。储热水箱中由于壁面对流换热等因素产生的低温热水会因密度大而聚集在水箱的底部，高温热水则会因密度较小而浮升到水箱的上部，从而实现不同温度的水在水箱内的温度分区。

(1) 建立水箱液体区域的无量纲瞬态控制方程,连续性方程、动量方程和能量方程分别如下:

(1)

其中,Ti、ui、p分别为量纲为1时的温度、速度、压力;Re为雷诺数;Ri为理查逊数,Ri=Gr/Re2(Gr为格拉晓夫数);Pe为贝克莱数,Pe=Re×Pr,Pr为普朗特数,Pr=ν/a，a为扩散率,ν为液体的运动黏度;T为液体温度;k为液体的导热系数。

(2) 矩形水箱在保温过程中,热传导导致的热损失量[7]为:

(2)

其中,A为保温材料表面积;Z为传热时间;λ为聚氨酯材料导热系数;δ为保温层厚度;Δt1为热水与环境间的温差。

3 数值模拟

本文使用有限体积法对上述数学模型进行求解[3]。为缩短计算时间,简化计算模型,忽略了水箱初始的温度分层以及检修口、进出水管对水箱的影响。

数值计算设置的初始条件为:水箱内部水温325.15 K,环境温度289.15 K,水箱外壁面与环境对流换热系数取10 W/(m2·K)[3];水箱底部加载10 ℃温度载荷。保温材料厚度设置为50 mm。设置水的密度为温度的函数。压力与速度耦合采用压力隐式分裂算子算法,采用二阶迎风格式离散动量项与能量项[8-12]。

仿真结束时,水箱最终温度云图如图3所示。由图3可以看出,水箱中上部水温较高,且温度分布较为均匀;中下部水温变化较为明显,有良好的温度分层,此现象在文献[3]中也有论述。受地面低温影响,水箱底部水温较低。水箱壁面附近水温均低于同一水平面其他区域水温。

图3 温度云图

使用Fluent软件分析水箱内部速度场,流体300 s与25 000 s时的速度云图分别如图4所示。由图4可知，水箱内部的速度场虽然处于很小的量级(10-3～10-5m/s),但是水箱始终处于一个动态的过程,正是由于这些流体的不断流动,水箱内部才会出现温度的分层。

初始时刻,由于水箱与外界环境温差较大,对流换热较强,产生的冷流体相对速度较大,不断向下流动,热流体不断向上浮动(见图4a);上壁面处的冷流体在向下流动时,会排开周围的液体[3](见图4b)。随着试验的进行,水箱温度整体降低,与外界环境温差逐渐减小,对流换热不断减弱,速度沿z轴负向(竖直向下)的流体不断减少,速度也不断降低,水箱内部最终达到一个平衡的状态。由于侧壁面不断向外散热,侧壁面附近始终存在不断向下流动的冷流体(见图4)。下壁面在散热过程中也会产生温度相对较低的冷流体,该部分冷流体相对密度较大,对水箱速度场并无较大的影响。水箱内部冷流体不断向下运动,热流体不断向上运动,两股流体交汇混合,因此在图4b中,有大部分区域处于-2.671×10-5～ 4.735×10-5m/s。

(a) 300 s

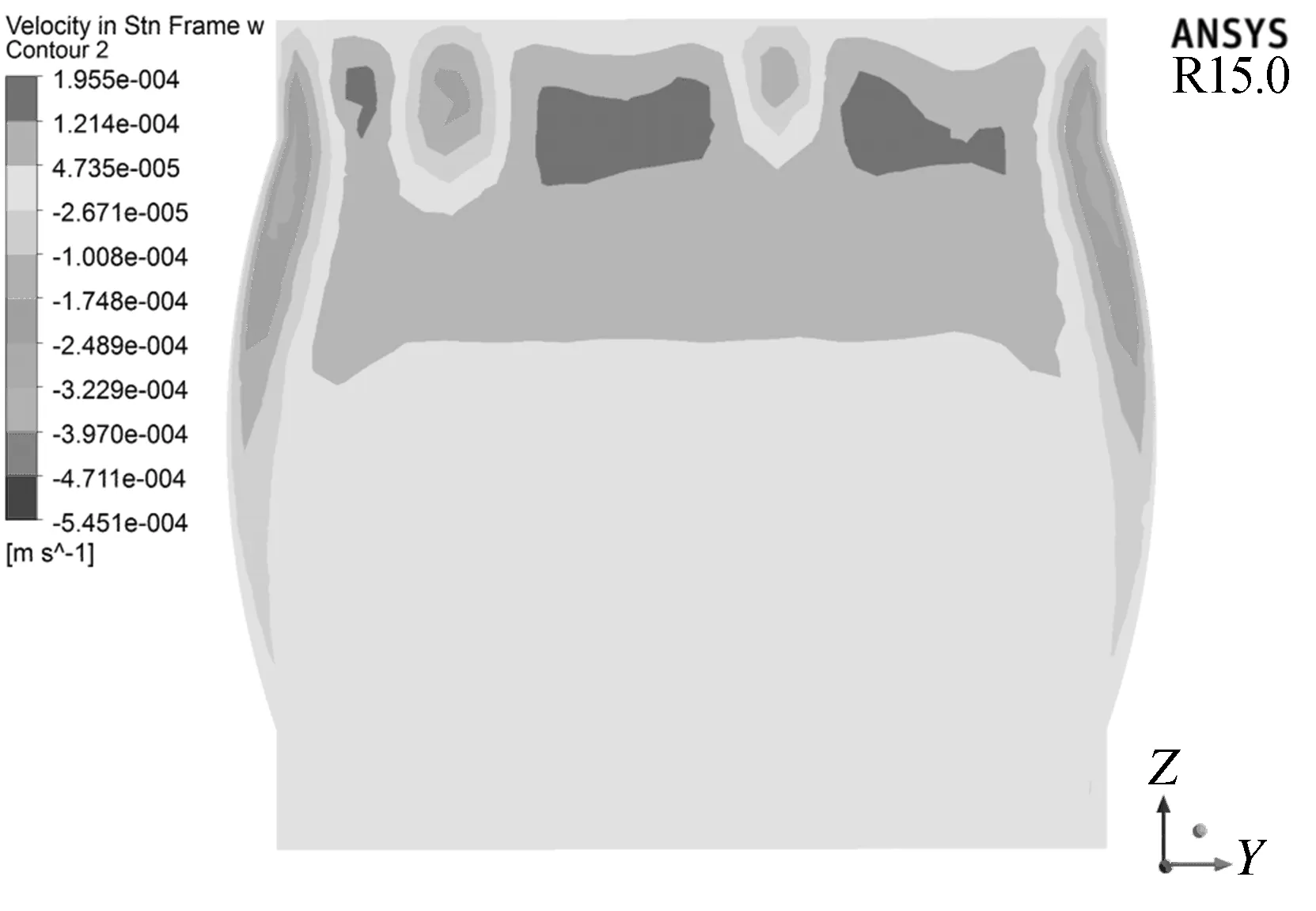
(b) 25 000 s

4 试验分析

(1) 在试验过程中,各测温点处的温度基本呈线性下降,如图5所示。38 h试验时间内,水箱温度降幅约为4.81 ℃,总热损失约为20 198.30 kJ;水箱热传导导致的热损失量可以由公式(2)计算得到,约为13 384.24 kJ。由此得出检修口处的漏热量约为6 814.06 kJ,占总热损失的33.74%。

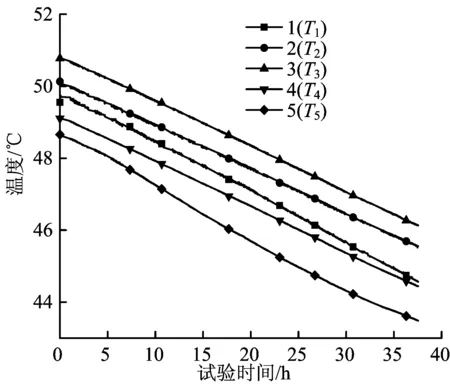
图5 各测点温度变化曲线

(2) 在试验过程中,水箱内部并没有出现自上而下的温度递减现象。试验数据表明,水箱中部的水温度最高,以此为界,水温向上和向下均出现递减现象,而上部水温梯度较小。由于计算机仿真忽略了水箱顶部检修口与外界的传质与传热,因而在图3中,水箱中上部温度较为均匀,未呈现明显的温度梯度。由此可见,检修口处的漏热对水箱中上部温度分布有较大的影响。

(3) 图5中曲线5的线性度较差,由2个方面因素造成:① 水箱置于地面,底面散热较强,对该处水温产生了较大的影响;② 上壁面、侧壁面对流换热以及检修口漏热产生的冷流体不断向下流动,对底部流体温度产生了一定的影响。

(4) 相邻测点温差值的曲线如图6所示。

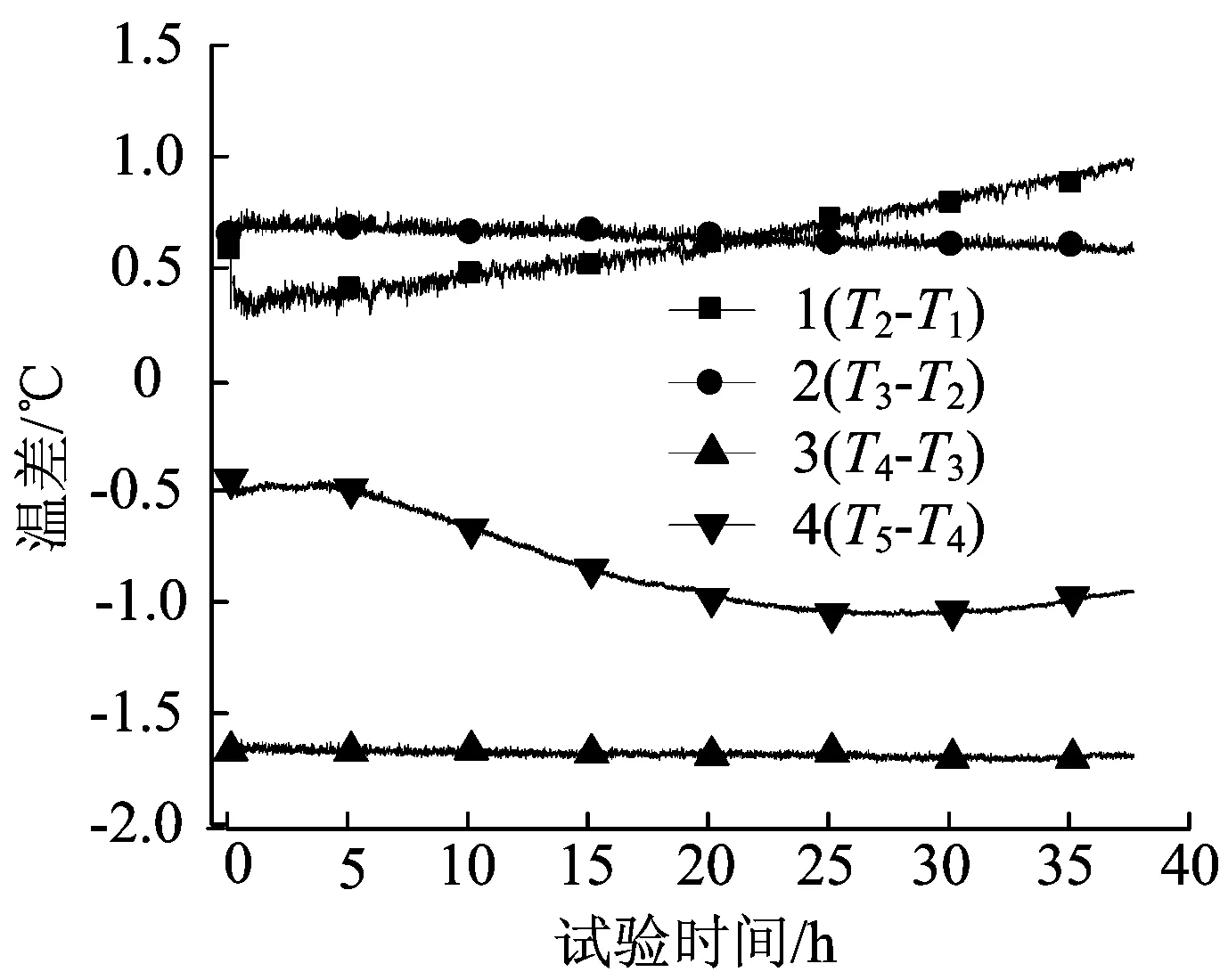
图6 相邻测点的温差曲线

测点2、1间温差逐渐增大,测点3、2间温差逐渐减小,测点3、4间温差基本恒定不变。随着水箱温度的整体降低,冷、热流体相对密度差逐渐减小,聚集在水箱顶部的冷流体逐渐增多,水箱上部温度梯度逐渐减小。由于分析(3)中2种因素产生的冷流体聚集在水箱底部,且体积逐渐增大,地面的低温使其加速向上扩散,致使水箱下部温度分层受到一定的破坏。因此,在5～25 h,测点4、5间温差在逐渐增大,而30 h后,该差值有减小的趋势。

(5) 测点3和测点5之间的温差最大，达至2.75 ℃,测点1、5间的温差最高达1.6 ℃。在实际工程当中,循环温差(集热器出口处的水温与水箱底部水温的差值)达到5 ℃时[13],温差循环泵启动,系统开始蓄热。随着水箱高度的增加,水箱内部温度梯度会进一步增大,文献[14]研究表明,在没有机械扰动的前提下,容积为450 L的水箱,水箱顶部与底部的温差最高可达32.4 ℃。故水箱底部的流体经过管道以及换热器之后,其温度依然会低于顶部流体温度。

绝大多数情况下,储热水箱的蓄热过程和放热过程会同时进行,这种循环温差的设置方式不仅会造成循环泵频繁启动,浪费电力能源,缩短控制系统与循环泵的寿命;而且会扰乱水箱已经形成的温度分层,增加辅助热源的能源消耗量,造成资源浪费。因此,循环温差应以水箱上部水温为基准进行设定。

5 结 论

(1) 本文试验过程中,各个测点(自上而下)处水温基本呈线性下降,水箱中下部分层良好。在试验后期,受壁面散热以及检修口漏热的影响,水箱中下部流体分层受到一定的破坏。

(2) 水箱检修口处漏热占总热损失为33.74%。因而在实际工程当中,要减少热损失,不仅要在各个壁面设置厚度合理的保温材料,还应在检修口外围增设保温装置,或对检修口的保温结构做出改进。

(3) 依据试验数据,且考虑到板式换热器换热温差以及管路的热损耗,循环温差应按以下方式设定:当集热器出口处水温高出水箱上部水温3～4 ℃时,系统开始蓄热。

[1] 钱锋. 解读太阳能建筑节能设计:以同济大学太阳能十项全能竞赛作品为例[C/OL]//国际绿色建筑与建筑节能大会, 2014. (2014-09-25)[2015-11-05]. http://d.wanfangdata.com.cn/Conference/8285130.

[2] LAVAN Z,THOMPSON T.Experimental study of thermally stratified hot water storage tanks [J].Solar Energy,1977,19(5):519-524.

[3] 杨征,陈海生,王亮,等.竖直圆柱形水箱保温过程热分层现象与机理研究[J].中国电机工程学报,2015,35(6):1420-1428.

[4] 韩延明,王如竹,代彦军,等.卧式热分区太阳能水箱内的贮热性能分析以及试验研究[J].太阳能学报,2008,29(3):277-282.

[5] 韩延明,王如竹,代彦军,等.新型太阳能温度分层水箱储能性能分析[J].化工学报,2006,57(增刊1):156-160.

[6] 于国清,汤金华,邹志军.太阳能热水系统蓄热水箱温度分层作用研究[J].建筑科学,2007,23(4):70-73.

[7] 於慧姝,陆春林,金苏敏.热泵热水器蓄热水箱的漏热损失分析[J].流体机械,2010,38(11):81-84.

[8] SIMON L,WAN X L.Numerical simulation of three-dimensional flow dynamics in a hot water storage tank [J].Applied Energy,2009,86(12):2604-2614.

[9] HAN Y M,WANG R Z,DAI Y J.Thermal stratification within the water tank [J]. Renewable and Sustainable Energy Reviews,2009,13(5):1014-1026.

[10] JOS F S,FRANCISCO J U,JAIME S.Experimental analysis of a domestic electric hot water storage tank, PartⅡ:dynamic mode of operation[J].Applied Thermal Engineering,2007,27(1):137-144.

[11] WAHIBA Y,MOHAMED G,EVGUENIY E,et al.Three-dimensional unsteady CFD simulations of a thermal storage tank performance for optimum design[J].Applied Thermal Engineering,2013,60(1):152-163.

[12] 王艳,吴超鹏.基于CFD方法的室内步行街排烟方案分析[J].合肥工业大学学报(自然科学版),2015,38(9):1291-1296.

[13] 郑瑞澄,路宾,李忠,等.太阳能供热采暖工程应用技术手册[M].北京: 中国建筑工业出版社,2012.

[14] 刘美杉,李详立,端木琳,等.跨季节水蓄热太阳能集中供暖工程与优化综述[J].建筑热能通风空调,2015,34(6):26-30.

(责任编辑 胡亚敏)

Numerical simulation and experimental research on insulation process of a rectangular water tank

TANG Jingchun1, MENG Xiaolei1, ZHANG Jian2

(1.School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China; 2.School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China)

The experiments on thermal stratification of rectangular solar heat storage water tank were carried out, and the reasons for internal thermal stratification in the tank were analyzed by numerical calculation. The results show that the internal fluid in the rectangular tank led to certain thermal stratification at the end of solar thermal storage. During the 38 hours of experiment, the temperature in the middle and lower part of the tank stratified well. Temperatures at each measuring point did not fluctuate wildly, basically descending linearly. However, the heat convection of the walls and the heat leakage had effect on the thermal stratification of the internal fluid. An improved method of setting up the cyclic temperature difference for the solar regenerative system was proposed based on the analysis of the experimental data and practical condition of engineering.

numerical calculation; experiment; rectangular water tank; thermal stratification; heat leakage

2016-01-22；

2016-09-01

合肥工业大学产学研校企合作资助项目(K-GD2014-0767);合肥工业大学博士学位专项基金资助项目(JZ2016HGBZ0748)

唐景春(1968-),男,安徽巢湖人,博士,合肥工业大学副教授,硕士生导师; 孟晓磊(1988-),男,山西朔州人,合肥工业大学硕士生,通讯作者,E-mail:mxlbmw760li@163.com.

10.3969/j.issn.1003-5060.2017.08.004

TK512.4

A

1003-5060(2017)08-1026-05