关于p-内平凡模的若干结论

黄文林

(中国人民大学信息学院，北京 100872)

关于p-内平凡模的若干结论

黄文林

(中国人民大学信息学院，北京 100872)

研究了p-内平凡kG-模的结构，证明了，p-内平凡的内p-置换kG-模V是有盖型的，此时，内p-置换kG-模V的盖与V作为p-内平凡模的盖是一致的.

p-内平凡模；内p-置换模；顶

0 引 言

在有限群表示论中，文献[1]首次引入p-可除kG-模来研究格林环中的幂零元素，p-可除kG-模是一类由有限群G的阶来控制的模类，它扩充了G上的投射模和相对投射模；内平凡kG-模是由Dade定义的模类[2]，它的内同态(自同态)环作为典范的kG-模在kG的稳定模范畴中是平凡的，它在kG的块代数的稳定模范畴的自等价、Dade群的结构等方面起着关键的作用[3-5]. 本文利用p-可除kG-模将内平凡kG-模扩充为p-内平凡kG-模.

p-内平凡kG-模V还是一种特殊的可裂迹OG-格，也就是，迹映射Tr:End(V)→O为可裂映射的OG-格V，文献[6]证明了可裂迹OG-格与关于O的几乎可裂序列的张量积一定不可裂，给出了OG-格的张量积的直和分解的方法.

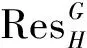
1 p-内平凡模

本文中，我们设定，p是素数，k是一个特征为p的代数封闭域，所有的群都是有限群，所有的模都是有限生成的. 记号和术语可参见文献[7-8].

对于有限群G和kG-模V，若V的任意不可分解直因子的维数能被p整除，则称V是一个p-可除kG-模[1].

本文限定，所有涉及p-可除kG-模的有限群G的阶都被p整除.

注1p-可除kG-模类是有限群G上的一个较大的模类，它包含所有的P-投射kG-模，这里P是G的真p-子群，特别地，它包含所有的投射kG-模([7，习题21.2，23.2])；但是，平凡kG-模k不是p-可除kG-模.

注2 设U，V是p-可除kG-模，W是kG-模，那么，U*，U⊕V，U⊗W，Hom(U，V)都是p-可除kG-模([1，性质2.2]).

注3 限制到代数封闭域k，由于任何不可分解kG-模都是绝对不可分解的，所以，文献[1]中的绝对p-可除模即是本文的p-可除kG-模，并得知，本文的p-可除kG-模本质上是由素数p完全控制的.

引理1 设H是G的子群，P是H的p-子群，U是kP-模，V是kG-模；

证明 1)由Krull-Schmidt定理即知结论成立.

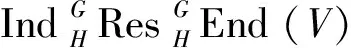
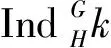
定义1 设V是kG-模，若内同态(自同态)模End(V)可以分解为平凡模和p-可除kG-模的直和，也即，End(V)=k⊕U，这里U是p-可除kG-模，那么，我们称V是p-内平凡kG-模.

注4 由注1知，p-内平凡kG-模的定义是合理的，它推广了熟知的(相对)内平凡模的概念[2，9]；平凡模k是最简单的p-内平凡kG-模，任何p-可除kG-模都不是p-内平凡kG-模.

引理2 设P是G的真p-子群，V是p-内平凡kG-模；那么，dim(V)=1 (p)，并且，任何p-内平凡kG-模都不是P-投射kG-模.

证明 End(V)=k⊕U，这里U是p-可除kG-模，那么，

由此，dim(V)=1 (p)；再由[7，习题23.2]得知，任何p-内平凡kG-模都不是P-投射kG-模.

性质1 设U和V是p-内平凡kG-模，W是P-可除kG-模，g∈G，n∈Z；那么，

1)V*是p-内平凡kG-模；

2)U⊗V是p-内平凡kG-模，反之也成立；

3) Hom(U，V)是p-内平凡kG-模；

4) Ωn(V) 是p-内平凡kG-模.

证明 1)设End(V)=k⊕M，这里M是p-可除kG-模，那么，End(V*)=(End(V))*=k⊕M*，由注2，M*是p-可除kG-模，由此，V*是p-内平凡kG-模.

2)设End(U)=k⊕U1，End(V)=k⊕V1，这里，U1和V1都是p-可除kG-模，那么，

End(U⊗V)≅ End(U)⊗ End(V)=(k⊕U1)⊗ (k⊕V1)≅k⊕U1⊕V1⊕(U1⊗V1)，

而由注2得知，U1⊕V1⊕(U1⊗V1)是p-可除kG-模，也即，U⊗V是p-内平凡kG-模；

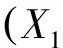
结合注2和Krull-Schmidt定理，得知，X1，Y1都是p-可除kG-模.

3)由1)、2)和kG-模同构Hom(U，V)≅U*⊗V，得知结论成立.

4)一方面，End(Ωn(V))≅Ωn(V)*⊗Ωn(V)≅Ω-n(V*)⊗Ωn(V)≅Ω0(V*⊗V)⊕(投射模)；另一方面，V*⊗V≅k⊕(p-可除模)≅Ω0(V*⊗V)⊕(投射模)；这说明，Ω0(V*⊗V)≅k⊕X，这里，X是非投射p-可除kG-模，由此，End(Ωn(V))是平凡模和p-可除kG-模的直和，也即，Ωn(V)是p-内平凡kG-模.

性质1表明，n次Heller算子Ωn(-)置换不可分解p-内平凡kG-模的同构类，它是不可分解非投射kG-模的同构类的子类([8，性质11.7.1]).

定理1 设V是p-内平凡kG-模，W是p-可除kG-模，那么，

1)V⊕W是p-内平凡kG-模；

2)在kG-模同构的意义下，V是它的唯一的不可分解p-内平凡直因子和一个p-可除kG-模的直和.

证明 1)由下面的典范的kG-模同构，

End(V⊕W)≅ End(V)⊕End(W)⊕Hom(V，W)⊕Hom(W，V)，

(1)

以及End(W)、Hom(V，W)、Hom(W，V)都是p-可除kG-模(注2)，得知，End(V⊕W)是平凡模和p-可除kG-模的直和，也即，V⊕W是p-内平凡kG-模.

2)相反，设U是V的不可分解非p-可除直因子，由典范同构式(1)、Krull-Schmidt定理，以及V是p-内平凡kG-模得知，End(U) =k⊕M，这里M是p-可除kG-模，也即，U是p-内平凡kG-模.

下面证明U是V的唯一的不可分解p-内平凡直因子. 若X是V的另一个不可分解p-内平凡直因子，由典范同构式(1)以及X是p-内平凡kG-模得知，k⊕k│End(V)，这与[10，定理2.1]相矛盾.

综上所述，在kG-模同构的意义下，V有唯一的不可分解p-内平凡直因子，并且，V是它的唯一的不可分解p-内平凡直因子和一个p-可除kG-模的直和.

注5 我们称定理1中的V的唯一的不可分解p-内平凡直因子为它的盖，定理1证明了，任何p-内平凡kG-模是它的盖和若干个不可分解p-可除kG-模的直和.

推论1 设0→U→W→V→0 是kG-模短正合列，若W是投射kG-模，那么，U是p-内平凡kG-模当且仅当V是p-内平凡kG-模.

证明 由Schanuel引理，可得到下面的kG-模同构：

U≅Ω(V)⊕U1，

(2)

V≅Ω-1(U)⊕V1，

(3)

式(2)和(3)中的U1和V1都是投射kG-模，由性质1的4)和定理1得知结论成立.

定理2 设H是G的子群，V是kG-模；

设End(V)=k⊕X，这里，X是kG-模；那么，

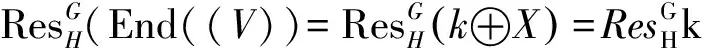
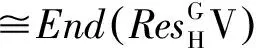
2)设End(V)=k⊕Y，这里，Y是p-可除kG-模；那么，

性质2 设H是G的子群，V是p-内平凡kG-模；若V是不可分解kG-模，那么，V的顶是G的西罗p-子群，并且，V从属于G的满亏p-块；若V是H-投射的，那么，H包含G的西罗p-子群.

证明 对第一部分应用反证法. 若不可分解模V的顶P是G的真p-子群，那么，由[7，习题23.2]得知，p│dim(V)，从而，再由引理1得知，V不是p-内平凡kG-模，矛盾；所以，不可分解模V的顶P是G的西罗p-子群.

若V从属于G的p-块B，那么，B的亏群包含V的顶P，从而，B的亏群也是G的西罗p-子群，也即，B是G的满亏p-块.

第二部分的证明. 由于H-投射kG-模的不可分解直因子仍是H-投射的，所以，结合第一部分的结论得知，H必须包含G的某个西罗p-子群.

注6 性质2说明，任何p-内平凡kG-模的盖的顶是G的西罗p-子群.

2 p-内平凡的内p-置换kG-模

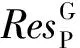
当P是G的真p-子群时，由注1得知，V是p-可除kG-模.

性质 3 设H是G的子群，U和V是内p-置换kG-模；

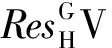
2)若V是p-内平凡kG-模，那么，Ωn(V) 是p-内平凡的内p-置换kG-模；

3)若U和V是p-内平凡kG-模，那么，U*和U⊗V都是p-内平凡的内p-置换kG-模.

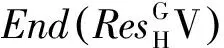
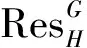
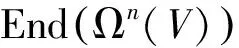
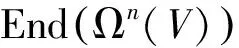
3)由性质1、[11，性质0.2]以及[7，性质28.2]得知结论成立.

定理3 设P是有限p-群，U是内平凡kP-模，V是不可分解有盖型内置换kP-模；那么，

1)U是有盖型内置换kP-模；

2)V是p-内平凡kP-模，并且，

(4)

这里，Q1，Q2，…，Qn是P的真p-子群.

证明 1)设End(U)=k⊕X，这里，X是投射kP-模，由[8，性质11.6.2]得知，X是1-投射kP-模，从而，X的每个不可分解直因子都是平凡源模，X是置换kP-模，U是内置换kP-模.

U是内平凡kP-模，那么，由性质2得知，U的盖的顶是G的西罗p-子群，由此，U是有盖型内置换kP-模.

2)设P是G的西罗p-子群，V是p-内平凡的内p-置换kG-模；那么，V有唯一的顶为P的不可分解直因子，从而，V是有盖型内p-置换kG-模，它的盖与p-内平凡kG-模V的盖重合；并且，End(V)=k⊕X，这里，X的任意不可分解直因子都是顶为G的真p-子群的平凡源模.

2)由定理1，设V=V1⊕L，这里，V1是V的唯一的不可分解p-内平凡直因子，L是p-可除kG-模，由性质2得知，V1的顶为G的西罗p-子群；L的任何不可分解直因子W是一个p-可除的内p-置换kG-模，由引理3得知，W的顶是G的真p-子群，由此，V的唯一的p-内平凡直因子是它的唯一的顶为G的西罗p-子群的直因子，也即，V有唯一的顶为P的不可分解直因子，从而，V是有盖型内p-置换kG-模，它的盖与p-内平凡kG-模V的盖重合.

设End(V)=k⊕X，这里X是p-可除kG-模，那么，X的任何不可分解直因子N都是p-可除kG-模，并且是p-置换kG-模[11]，从而，由引理3得知，N的顶是G的真p-子群，这说明，X的任何不可分解直因子是顶为G的真p-子群的平凡源kG-模.

[1] BENSON D，CARLSON J. Nilpotent elements in the Green ring[J]. J Alg, 1986, 104(2): 329-350.

[2] DADE E. Endo-permutation modules overp-groups, II[J]. Ann of Math, 1978, 108: 317-346.

[3] BOLTJE R, XU B. Onp-permutation equivalences: Between Rickard equivalences and isotypies[J].Trans Amer Math Soc, 2008, 360(10): 5067-5087.

[4] PEREPELITSKY P.p-permutation equivalences between blocks of finite groups[D]. California: University of California, 2014.

[5] ROUQUIER R. Block theory via stable and Rickard equivalences[C]∥Modular Representation Theory of Finite Groups，Berlin:de Gruyter, 2001: 101-146.

[6] AUSLANDER M，CARLSON J. Almost-split sequences and group rings[J]. J Alg, 1986, 103: 122-140.

[7] THEVENAZ J.G-algebras and modular representation theory[M]. New York: Clarendon Press Oxford Univ Press, 1995.

[8] WEBB P. A course in finite group representation theory[M]. New York: Cambridge Univ Press,Pre-publication Version, 2016.

[9] LASSUEUR C. Relative projectivity and relative endotrivial modules[J]. J Alg, 2012, 337(1): 285-317.

[10] BENSON D. Representations and cohomology. I[M]. New York: Cambridge Univ Press, 1998.

[11] BROUE M. On Scott module andp-permutation modules: an approach through the Brauer morphism[J]. Proc Amer Math Soc, 1985, 93(3): 401-408.

Some Results on thep-endotrivialkG-modules

HUANG Wenlin

(School of Information，Renmin University of China，Beijing 100872，China)

This paper studies thep-endotrivialkG-module, and proves that any endo-p-permutationkG-moduleVwhich isp-endotrivial at the same time must be capped, and the moment, the cap of the endo-p-permutationkG-moduleVis the same as that ofVas ap-endotrivialkG-module.

p-endotrivial module；endo-p-permutation module；vertex

2016-11-09

国家自然科学基金项目(10826057).

黄文林(1977—)，男，博士，主要从事有限群表示论研究. E-mail: wenlinhuang@163.com

10.3969/j.issn.1674-232X.2017.04.014

O152.6 MSC2010：20C05； 20C20

A

1674-232X(2017)04-0424-06