2-距离空间中(ψ,φ,θ)-压缩映象的公共耦合不动点定理

刘丽亚，谷 峰

(杭州师范大学理学院，浙江 杭州 310036)

2-距离空间中(ψ,φ,θ)-压缩映象的公共耦合不动点定理

刘丽亚，谷 峰

(杭州师范大学理学院，浙江 杭州 310036)

在完备的2-距离空间中, 通过讨论一类(ψ,φ,θ)-压缩条件, 研究了耦合重合点和耦合公共不动点的存在性和唯一性问题，从而得到一个新的公共耦合不动点定理，改进了相关文献的结果.

完备2-距离空间; (ψ,φ,θ)-压缩映象; 耦合重合点; 耦合公共不动点; 混合g-单调性

1 引言和预备知识

1963年, Gähler[1]首次引入了2-距离空间的概念. 1976年, Iséki等[2]开始研究关于2-距离空间中映象的不动点问题. 近年来, 2-距离空间中的不动点理论得到了较大的发展[3-8]. 受上述文献的启发, 该文在完备的2-距离空间中, 引入一类新的(ψ,φ,θ)-压缩条件, 并在此条件下研究耦合重合点和公共耦合不动点的存在性和唯一性问题, 得到了一个新的耦合公共不动点定理, 在很大程度上改进和发展了相关文献的一些已知结果.

在介绍主要结果之前, 先介绍一些基本概念和已知结果.

定义1[8]设X是非空集,d:X×X×X→[0,+),满足：

1) 对每一对点a,b∈X,a≠b, 存在一点c∈X, 使得d(a,b,c)≠0;

2)d(a,b,c)=0, 当a,b,c中至少有二元相等;

3)d(a,b,c)=d(a,c,b)=d(b,c,a)=d(b,a,c)=d(c,a,b)=d(c,b,a);

4)d(a,b,c)≤d(a,b,x)+d(a,x,c)+d(x,b,c), 其中x是X中的任一元.

则称(X,d)为2-距离空间.

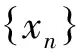
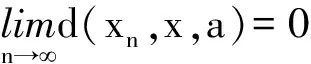
定义4[8]2-距离空间(X,d)称为完备的, 如果X中的每一Cauchy列都是X中的收敛列.

引理1[8]设(X,d)为2-距离空间. 对于任意一序列{xn}→x∈X, 那么有

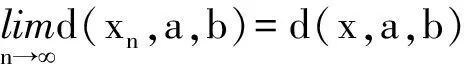
注1[8]正如Gähler[1]证明了, 尽管2-距离空间d对每一个变元都是连续的, 但它不必对二变元同时连续; 如果对任二变元同时连续, 则必同时对三变元连续.

定义5[9]称(x,y)∈X×X是映象F:X×X→X 的耦合不动点, 如果F(x,y)=x,F(y,x)=y.

定义6[11]称(x,y)∈X×X是映象对F:X×X→X和g:X→X 的耦合重合点, 如果F(x,y)=gx,F(y,x)=gy.

定义7[11]称(x,y)∈X×X是映象对F:X×X→X和g:X→X 的耦合公共不动点,如果F(x,y)=gx=x,F(y,x)=gy=y.

定义8[11]设X为一非空集. 映象对F:X×X→X和g:X→X称为是w-相容, 当F(x,y)=gx,F(y,x)=gy时, 满足gF(x,y)=F(gx,gy)成立.

定义9[12]设(X,⪯)是一偏序集, 函数T:X×X→X,g:X→X. T称为具有混合g-单调性质, 如果T(x,y)在x处是g-单调不减, 在y处是g-单调不增, 即对任意的x,y∈X, 有

x1,x2∈X,gx1⪯gx2⟹T(x1,y)⪯T(x2,y);

y1,y2∈X,gy1⪯gy2⟹T(x,y1)T(x,y2).

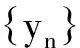
(i) mi>ni+1,ni→(i→);

(ii) d(ymi,yni,a0)≥ε0;d(ymi-1,yni,a0)<ε0,i=1,2,3,….

2 主要结果

该文处处假设以下3种类型的函数[13]：

定理1 设(X,⪯)是完备2-距离空间(X,d)上的一偏序集. g:X→X为X上的自映象. 映象T:X×X→X具有混合g-单调性, 且与g可交换. g,T都为连续映象. 实数M∈R. 如果满足以下条件：

1) T(X×X)⊆g(X);

2) ∃(x0,y0)∈X×X使得 gx0⪯T(x0,y0),gy0T(y0,x0);

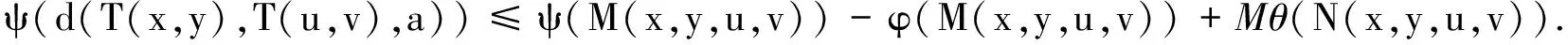
(1)

其中

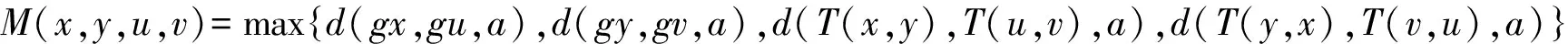
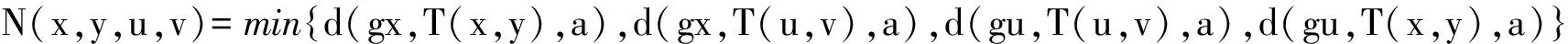
则g和T在X中有耦合重合点.

证明 由条件(2)可得, ∃(x0,y0)∈X×X使得gx0⪯T(x0,y0),gy0T(y0,x0), 由于T(X×X)⊆g(X), 则∃x1,y1∈X, 使得gx1=T(x0,y0),gy1=T(y0,x0).同样道理, ∃x2,y2∈X, 使得gx2=T(x1,y1),gy2=T(y1,x1). 由gx0⪯T(x0,y0),gy0T(y0,x0), 可知gx0⪯gx1,gy0gy1. 由于映象T具有混合g-单调性, 所以可知

gx1=T(x0,y0)⪯T(x0,y1)⪯T(x1,y1)=gx2;

gy1=T(y0,x0)T(y0,x1)T(y1,x1)=gy2.

这样继续做下去就可得到X中的两个序列{gxn}和{gyn}, 分别为

gxn=T(xn,yn)和gyn=T(yn,xn).

且{gxn}和{gyn}满足

gx0⪯gx1⪯gx2⪯…⪯gxn⪯gxn+1⪯…,

(2)

gy0gy1gy2…gyngyn+1….

(3)

在式(1)中令(x,y)=(xn,yn)和(u,v)=(xn+1,yn+1), 由式(2)和(3)可得

ψ(d(gxn+1,gxn+2,a))=ψ(d(T(xn,yn),T(xn+1,yn+1),a))≤

ψ(M(xn,yn,xn+1,yn+1))-φ(M(xn,yn,xn+1,yn+1))+Mθ(N(xn,yn,xn+1,yn+1)).

(4)

其中

(5)

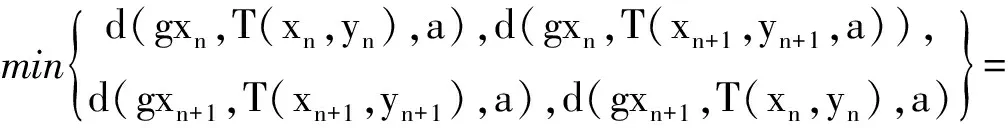
(6)

由式(4)—(6)得

ψ(d (gxn+1,gxn+2,a))≤

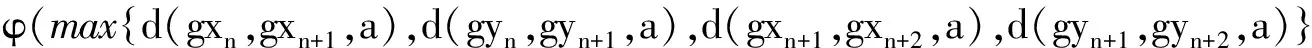
(7)

同样道理, 可得

ψ(d(gyn+1,gyn+2,a))≤

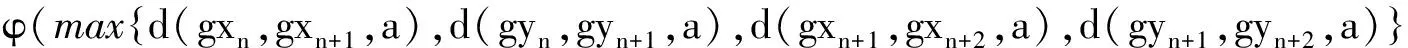
(8)

令

δn=max{d(gxn,gxn+1,a),d(gyn,gyn+1,a)}.

(9)

由于max{ψ(a),ψ(b)}=ψ(max{a,b}),∀a,b∈[0,+), 可得

ψ(δn+1)=max{ψ(d(gxn+1,gxn+2,a)),ψ(d(gyn+1,gyn+2,a))}.

(10)

再由式(7)—(10)得

ψ(δn +1)≤

ψ(max{d(gxn,gxn+1,a),d(gyn,gyn+1,a),d(gxn+1,gxn+2,a),d(gyn+1,gyn+2,a)})-

φ(max{d(gxn,gxn+1,a),d(gyn,gyn+1,a),d(gxn+1,gxn+2,a),d(gyn+1,gyn+2,a)})=

ψ(max{δn+1,δn})-φ(max{δn+1,δn}).

(11)

如果δn+1>δn(δn+1>0, 否则δn<0, 出现矛盾), 此时式(11)可整理为

ψ(δn+1)≤ψ(δn+1)-φ(δn+1)<ψ(δn+1).

结果出现矛盾,故

δn+1≤δn,n=0,1,2,….

(12)

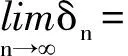
(13)

结合式(12), 式(11)可整理为

δn+1≤ψ(δn)-φ(δn).

(14)

ψ(δ)≤ψ(δ)-φ(δ)<ψ(δ).

出现矛盾 , 于是δ=0, 即

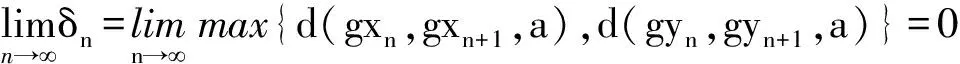
那么有

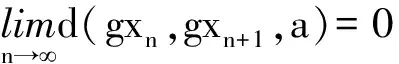
(15)

下面将证明

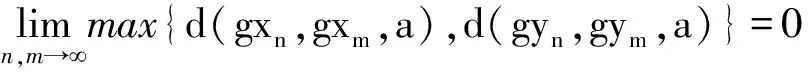
(16)

若不然，由引理1知, 必存在某一a0∈X和某一ε0>0, 且存在正整数列{mi},{ni}, 使得

(i) mi>ni+1,ni→(i→)；

(ii)max{d(gxni,gxmi,a0),d(gyni,gymi,a0)}≥ε0,max{d(gxni,gxmi-1,a0),d(gyni,gymi-1,a0)}<ε0,i=1,2,3,….

运用三角不等式，得

d(gxni,gxmi,a0)≤d(gxni,gxmi,gxmi-1)+d(gxni,gxmi-1,a0)+d(gxmi-1,gxmi,a0);

d(gyni,gymi,a0)≤d(gyni,gymi,gymi-1)+d(gyni,gymi-1,a0)+d(gymi-1,gymi,a0).

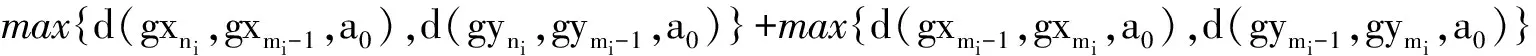
(17)

再次运用三角不等式得

d(gxni-1,gxmi-1,a0)≤d(gxni-1,gxmi-1,gxni)+d(gxni-1,gxni,a0)+d(gxni,gxmi-1,a0);

d(gyni-1,gymi-1,a0)≤d(gyni-1,gymi-1,gyni)+d(gyni-1,gyni,a0)+d(gyni,gymi-1,a0).

(18)

利用式(15)和条件(ii), 并将式(17)和(18)两边令i→, 取极限, 可得

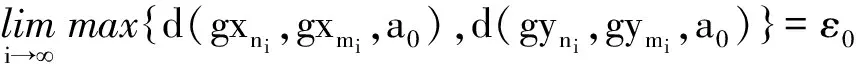
(19)

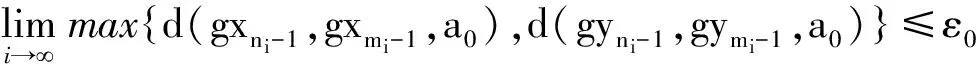
(20)

由式(1)可得

ψ(d(gxni,gxmi,a0))= ψ(d(T(xni-1,yni-1),T(xmi-1,ymi-1),a0))≤

ψ(M(xni-1,yni-1,xmi-1,ymi-1))-φ(M(xni-1,yni-1,xmi-1,ymi-1))+

Mθ(N(xni-1,yni-1,xmi-1,ymi-1)).

(21)

其中

M(xni-1,yni-1,xmi-1,ymi-1)=

(22)

(23)

将式(22)和(23)代入(21), 两边令i→时, 取极限, 并将式(15),(19)和(20)代入得

即得

ψ(ε0)≤ψ(ε0)-φ(ε0)<ψ(ε0).

由此推出矛盾. 即证得式(16)成立, 进而可知

又因为2-距离空间(X,d)是完备的, 所以∃x,y∈X, 使得

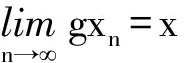
(24)

由g和T的可交换性, 可得

g(gxn+1)=g(T(xn,yn))=T(gxn,gyn), g(gyn+1)=g(T(yn,xn))=T(gyn,gxn).

(25)

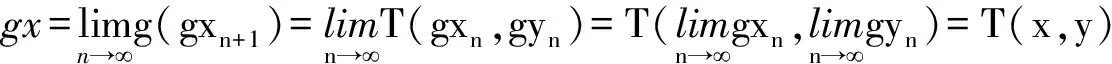
于是可得,(x,y)是g和T的耦合重合点,即gx=T(x,y),gy=T(y,x).证毕.

定理2 设(X,⪯)是完备2-距离空间(X,d)上的一偏序集.g:X→X为X上的自映象. 映象T:X×X→X具有混合g-单调性, 且与g可交换.g,T都为连续映象. 实数M∈R. 如果满足以下条件:

1)T(X×X)⊆g(X);

2) ∃(x0,y0)∈X×X使得gx0⪯T(x0,y0),gy0T(y0,x0);

3) ∀x,y,u,v,a∈X, 如果gx⪯gu,gygv或者gxgu,gygv, 那么有(x,y,u,v)).其中

则g和T在X中有耦合重合点.

证明 与定理 1 证明方法相同, 略去.

推论1 设(X,⪯)是完备2-距离空间(X,d)上的一偏序集.g:X→X为X上的自映象. 映象T:X×X→X具有混合g-单调性, 且与g可交换.g,T都为连续映象. 实数M∈R. 如果满足以下条件:

1) T(X×X)⊆g(X);

2) ∃(x0,y0)∈X×X使得 gx0⪯T(x0,y0),gy0T(y0,x0);

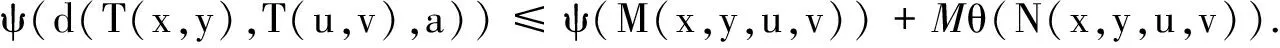
其中：

.

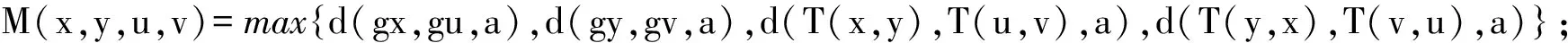
则g和T在X中有耦合重合点.

推论2 设(X,⪯)是完备2-距离空间(X,d)上的一偏序集. I:X→X为X上的恒等映象. 映象T:X×X→X具有混合I-单调性, 且与g可交换. g,T都为连续映象. 实数M∈R. 如果满足以下条件:

1) T(X×X)⊆g(X);

2) ∃(x0,y0)∈X×X使得 gx0⪯T(x0,y0),gy0T(y0,x0);

其中：

.

则T在X中有耦合不动点.

证明 令定理1中的自映象g为恒等映象I, 即可证得.

3 不动点的唯一性

设(X,⪯)是偏序集, 我们在2-距离空间(X,d)中规定一种可比较关系如下:

定理3 在定理1中, 对于g和T的任意两个耦合重合点(x*,y*)和(z*,t*), 都能找到(u*,v*)∈X×X, 使得(gu*,gv*)分别和(gx*,gy*),(gz*,gt*)满足以上可比较关系, 这时, g和T有唯一的耦合重合点和唯一的耦合公共不动点.

证明 由定理1可知, g,T至少存在一个耦合重合点. 设(x,y)和(z,t)是g,T任意两个耦合重合点, 即T(x,y)=gx,T(y,x)=gy和T(z,t)=gz,T(t,z)=gt. 现证(gx,gy)=(gz,gt).

由于∃(u,v)∈(X×X), 使得(gu,gv)分别和(gx,gy),(gt,gz)满足以上可比较关系.

情况1 当可比较关系为

(gx,gy)⪯(gu,gv),(gt,gz)⪯(gu,gv).

(26)

令u0=u,v0=v,则∃(u1,v1)∈X×X, 使得gu1=T(u0,v0),gv1=T(v0,u0).依次类推, 会得到两个数列{gun}和{gvn}分别为gun+1=T(un,vn),gvn+1=T(vn,un),n=1,2,3,….令

x0=x,y0=y，z0=z,t0=t.

(27)

同样道理, 可以得到数列{gxn},{gyn}和{gzn},{gtn}分别为

gxn+1=T(xn,yn),gyn+1=T(yn,xn),n=0,1,2,….

gzn+1=T(zn,tn),gtn+1=T(tn,zn),n=0,1,2,….

由于(x,y)是g,T的耦合重合点, 则有

gx1=T(x0,y0)=T(x,y)=gx=gx0,gy1=T(y0,x0)=T(y,x)=gy=gy0；

gx2=T(x1,y1)=T(x0,y0)=gx1,gy2=T(y1,x1)=T(y0,x0)=gy1.

依次类推可知gx0=gx1=…=gxn=…,gy0=gy1=…=gyn=…. 即

gxn=gx,gyn=gy,∀n=0,1,2,….

(28)

相同道理可知

gzn=gz,gtn=gt,∀n=0,1,2,….

(29)

由于式(26)和(27)可整理为

(gx0,g0)⪯(gu0,gv0),(gt0,gz0)⪯(gu0,gv0).

又T具有混合g-单调性, 所以

即(gx1,gy1)⪯(gu1,gv1).同样道理, 有(gx2,gy2)⪯(gu2,gv2). 这样继续做下去, 可得

(gxn,gyn)⪯(gun,gvn),n=0,1,2,….

类似方法,可得

(gtn,gzn)⪯(gun,gvn),n=0,1,2,….

结合式(28)和(29)可得

(gx,gy)⪯(gun,gvn),(gt,gz)⪯(gun,gvn).

由式(1)得到

ψ(d(gx,gun+1,a))=ψ(d(T(x,y),T(un,vn,a))≤

ψ(M(x,y,un,vn))-φ(M(x,y,un,vn))+Mθ(N(x,y,un,vn)).

(30)

其中

M(x,y,un, vn)=

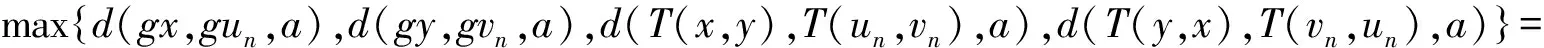
N(x,y,un,vn)=

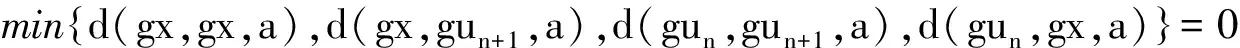
于是式(30)整理为

ψ(d(gx,gun+1,a))≤

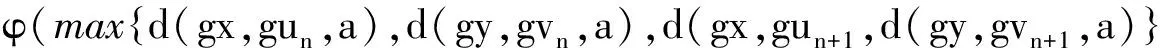
(31)

同理可得

ψ(d(gy,gvn+1,a))≤

(32)

现令

(33)

联立式(31)—(33), 又由max{ψ(a),ψ(b)}=ψ(max{a,b}),∀a,b∈[0,+), 得到

(34)

设γn<γn+1.γn+1>0(否则γn<0 , 出现矛盾).

此时式(34)可整理为

ψ(γn+1)≤ψ(γn+1)-φ(γn+1)<ψ(γn+1).

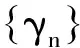
进而可知

(35)

同样道理可证得

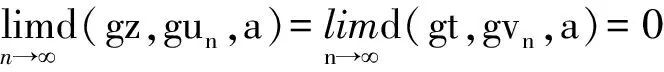
(36)

由式(35)和(36)得到

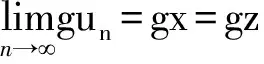
即(gx,gy)=(gz,gt). 所以g和T具有唯一的耦合重合点. 又因为g和T具有可交换性, 得到

g(gx)=g(T(x,y))=T(gx,gy),g(gy)=g(T(y,x))=T(gx,gy).

(37)

由于∃m,n∈X, 使得gx=m,gy=n, 那么式(37)可整理为

gm=T(m,n),gn=T(n,m).

(38)

因此(m,n)也是g和T的一个耦合重合点, 由耦合重合点的唯一性知gm=gx=m,gn=gy=n. 又由式(38)可得m=gm=T(m,n),n=gn=T(n,m).即证得g和T有耦合公共不动点. 由于g和T的耦合重合点具有唯一性, 因此g和T的耦合公共不动点也具有唯一性.

情况2 当可比较关系为(gu,gv)⪯(gx,gy),(gt,gz)⪯(gu,gv).

情况3 当可比较关系为(gx,gy)⪯(gu,gv),(gu,gv)⪯(gt,gz).

情况4 当可比较关系为(gu,gv)⪯(gx,gy),(gu,gv)⪯(gt,gz).

同情况1的证明方法类似, 上述3种情况同样也能证得g和T的耦合公共不动点也具有唯一性.

[1]GHERS.2-metrischeRäumeundihretopogischeStruktur[J].MathNachr,1963,26(1/2/3/4):115-148.

[2]ISÉKIK.Fixedpointtheoremsin2-mericspaces[J].MathSeminarNotes,KobeUniv,1975,3(1):133-136.

[3]DESHPANDEB,CHOUHANS.Commonfixedpointtheoremsforhybridpairsofmappingswithsomeweakerconditionsin2-mericspaces[J].FascMath,2011,46:37-55.

[4]ALIOUCHEA,SIMPSONC.Fixedpointsandlinesin2-metricspaces[J].AdvMath,2012,229(1):668-690.

[5]LAHIRIBK,DASP,DEYLK.Cantor’stheoremin2-metricspacesanditsapplicationstofixedpointproblems[J].TaiwanJMath,2011,15(1):337-352.

[6]LIUZQ,ZHANGF.Characterizationsofcommonfixedpointsin2-metricspace[J].RostockMathKolloq,2001,55(1):49-64.

[7]DUBEYRP.Somefixedpointtheoremsonexpansionmappingsin2-metricspaces[J].PureApplMathSci,1990,32(1):33-37.

[8] 张石生.不动点理论及其应用[M].重庆:重庆出版社,1984.

[9]BHASKARTG,LAKSHMIKANTHAMV.Fixedpointtheoremsinpartiallyorderedmetricspacesandapplications[J].NonlinearAnal,2006,65(7):1379-1393.

[10]CHOUDHURYBS,MAITYP.Coupledfixedpointresultsingeneraliaedmetricspaces[J].MathComputModelling,2011,54(1/2):73-79.

[11]LAKSHMIKANTHAMV,IRIL.Coupledfixedpointtheoremsfornonlinearcontractionsinpartiallyorderedmetricspaces[J].NonlinearAnal, 2009, 70(12):4341-4349.

[12]BERINDEV,BORCUTM.Tripledfixedpointtheoremsforcontractivetypemappingsinpartiallyorderedmetricspaces[J].NonlinearAnal, 2011,74(15):4889-4897.

[13] 谷峰.不动点定理与非线性算子迭代序列的收敛性[M].哈尔滨：黑龙江科技出版社,2002.

A Common Fixed Point Theorem of (ψ,φ,θ)-contractive Mappings in 2-metric Spaces

LIU Liya，GU Feng

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

In complete 2-metric spaces, by discussing a class of (ψ,φ,θ)-contractive condition, the existence and the uniqueness of the coupled coincidence point and coupled common fixed point were studied, then a new common coupled fixed point theorem was obtained, which improved the corresponding results in some references.

complete 2-metric space; (ψ,φ,θ)-contractive mappings; coupled coincidence point; coupled common fixed point; mixedg-monotone property

2016-06-04

国家自然科学基金项目(11071169)；浙江省自然科学基金项目(Y6110287).

谷 峰(1960—), 男,教授, 主要从事非线性泛函分析及应用研究. E-mail：gufeng99@sohu.com

10.3969/j.issn.1674-232X.2017.04.013

O177.91 MSC(2010)：47H10； 54H25

A

1674-232X(2017)04-0416-08