基于偏航的风力机尾迹偏移控制流动机理研究
缪维跑, 李 春,2, 阳 君,2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
基于偏航的风力机尾迹偏移控制流动机理研究
缪维跑1, 李 春1,2, 阳 君1,2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
通过非定常CFD方法模拟在大气边界层环境下2台串列布置的全尺寸5 MW风力机组,研究在风场多尺度流动特性下基于偏航的尾迹控制方法导致尾迹偏移的流动机理.结果表明:上游风力机偏航可有效提高风场总功率;速度场分析显示偏航时尾迹发生形变,而涡量场分析表明偏航的尾迹在传播过程中将产生一对逆时针旋转的涡,从而导致尾迹在宏观上表现为偏移;尾迹偏移效果仅在轮毂高度处较为显著,发生形变的尾迹低速区仍会向其余区域扩散.
尾迹控制; 偏航; 水平轴风力机; 叶尖涡; CFD
为提高土地及风资源的利用率,现代风场通常布置多排风力机组同时运行[1].为减缓机组间的尾迹效应,提高风场的总输出功率,基于风场布局的传统方法在设计阶段规划风力机组的位置[2],或协同运行不同风轮直径、塔架高度和间距的风力机组[3-4].但此类尾迹被动控制方法的效率在风况发生变化时可能有所降低,尤其当风轮进行偏航对风时上游风力机的尾迹可能严重影响下游风力机.
为了减缓对下游风力机的干扰,近期研究方向转向主动控制风场尾迹.一种尾迹控制方法是控制尾迹的流向,即当风力机组对准入流风向时,有意使上游风力机处于偏航状态,从而使尾迹流向偏移以避开下游风力机,进而使下游风力机的功率增大以补偿上游风力机的功率损失.Jiménez等[5]首先提出该方法并使用大涡模拟结合制动盘模型进行数值模拟,而Wagenaar等[6]和Andresen[7]则通过实验方法验证了此基于偏航尾迹控制策略的有效性.Fleming等[8-9]模拟了在大气边界层环境下上游风力机不同偏航角度对风场全局功率性能的影响,并提出使用仰角或独立变桨的方法诱导上游风力机产生横向力以偏移尾迹的轨迹.
然而,上述研究均基于制动盘模型(Actuator Disk Model,ADM)或制动线模型(Actuator Line Model,ALM),尽管制动模型可减少计算量,但需添加额外的工程经验模型用于模拟风轮的旋转,且通常忽略了机舱和塔架的影响,从而降低了真实性及三维流动效果[10-12].此外,制动模型计算的风场尾迹可能低估了尾迹速度亏损持续性,与使用全尺寸风轮模型(Full-scale RotorModel,FRM)模拟的结果相比,其尾迹将在更短距离内恢复速度亏损,从而高估了下游风力机的功率输出[13].因此,笔者使用全尺寸风力机模型模拟在大气边界层(Atmospheric Boundary Layer,ABL)环境下2台串列布置的5 MW风力机,更为细致地研究在风场多尺度流动特征下基于偏航的尾迹控制方法的流动机理以及对下游风力机的影响.
1 数值模拟
1.1 风力机模型
以美国可再生能源实验室(National Renewable Energy Laboratory,NREL)发布的5 MW海上风力机[14]为研究对象,主要设计参数见表1.通过CAD建立的几何模型如图1所示,包括轮毂、机舱及塔架.制动模型忽略了塔架及机舱,因此无法考虑塔影效应对尾迹的影响.
1.2 风场布置
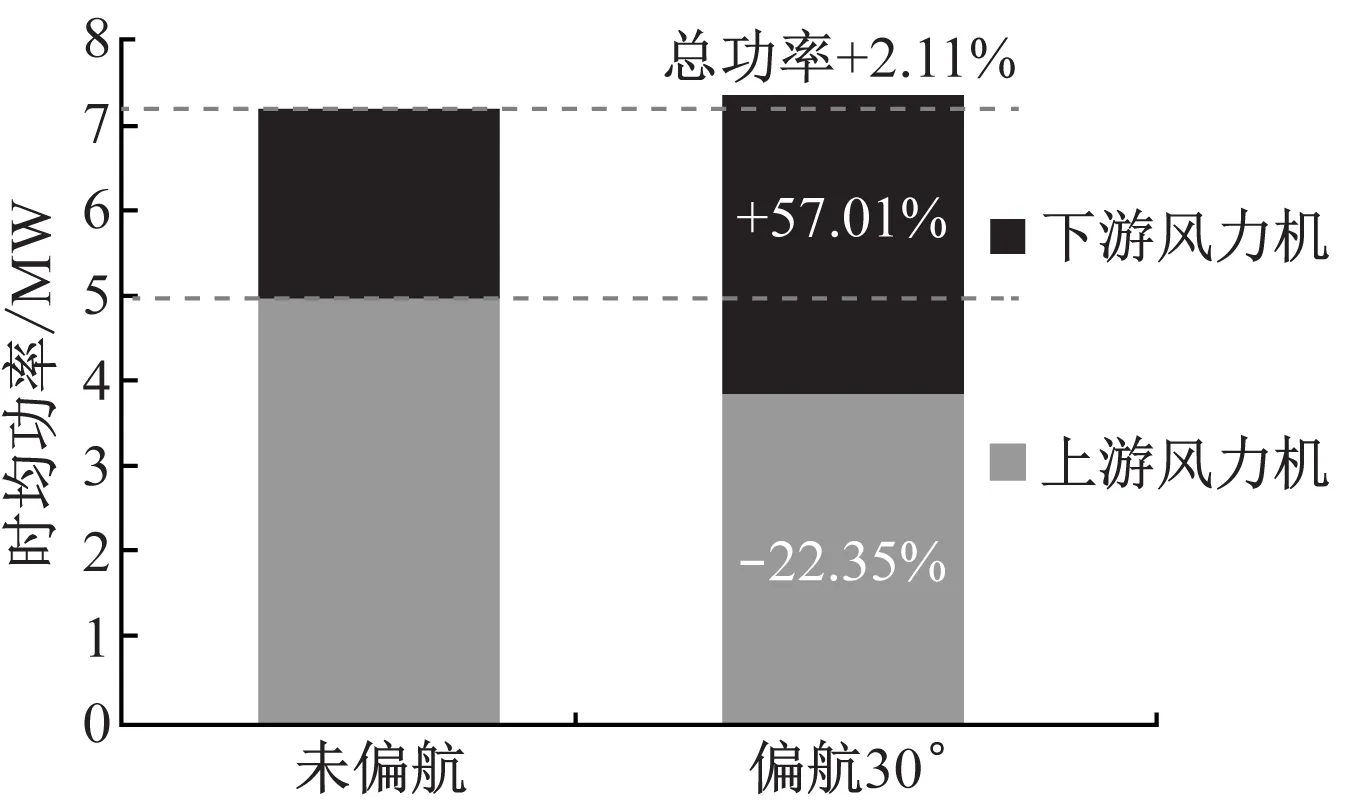
为研究尾迹的偏移运动,串列布置2台5 MW风力机,其风轮转动方向皆为顺时针,计算过程中根据风轮平面的平均风速调整风力机转速,以保证最佳叶尖速比.两风力机的间距越大,尾迹的速度亏损恢复得越完整,但受限于土地面积和电缆连接所耗成本,该间距不宜过大[15].因此,两风力机的间距选用标准的7倍[16]风轮直径距离(7D=882 m).文献[9]的研究结果表明,尾迹偏移的程度及风场总功率受上游风力机偏航角度的影响,如图2所示.为研究偏航尾迹流动特性,选取效果相对较好的30°偏航角工况进行数值模拟,同时与未偏航工况(即0°偏航角)进行对比.
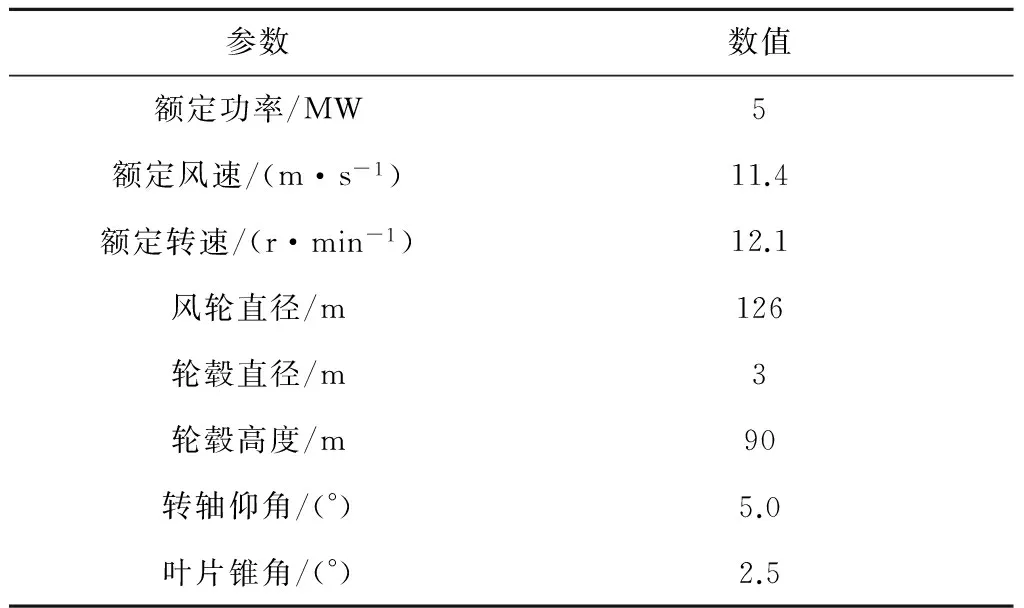
表1 NREL 5 MW风力机设计参数
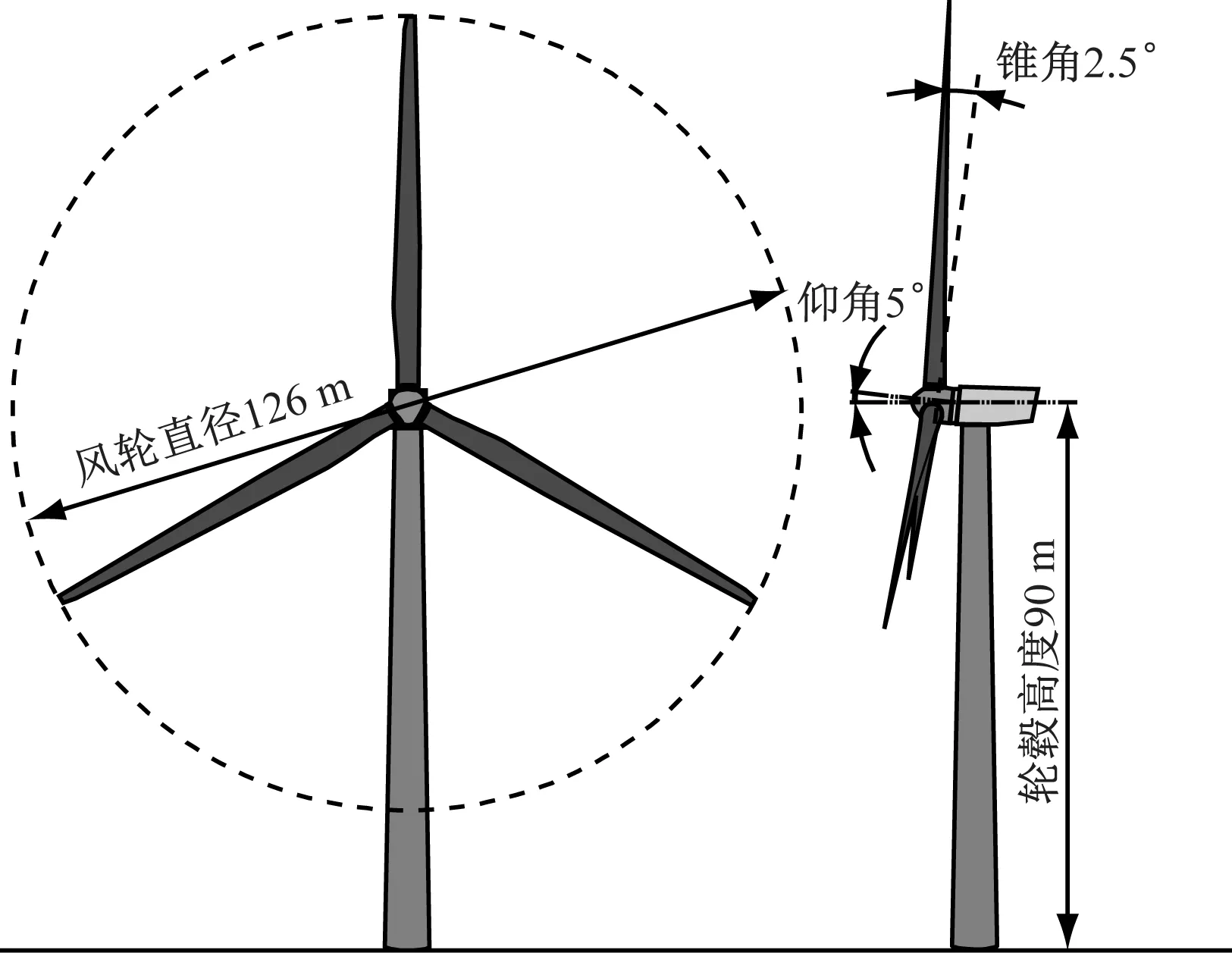
图1 NREL 5 MW风力机几何模型
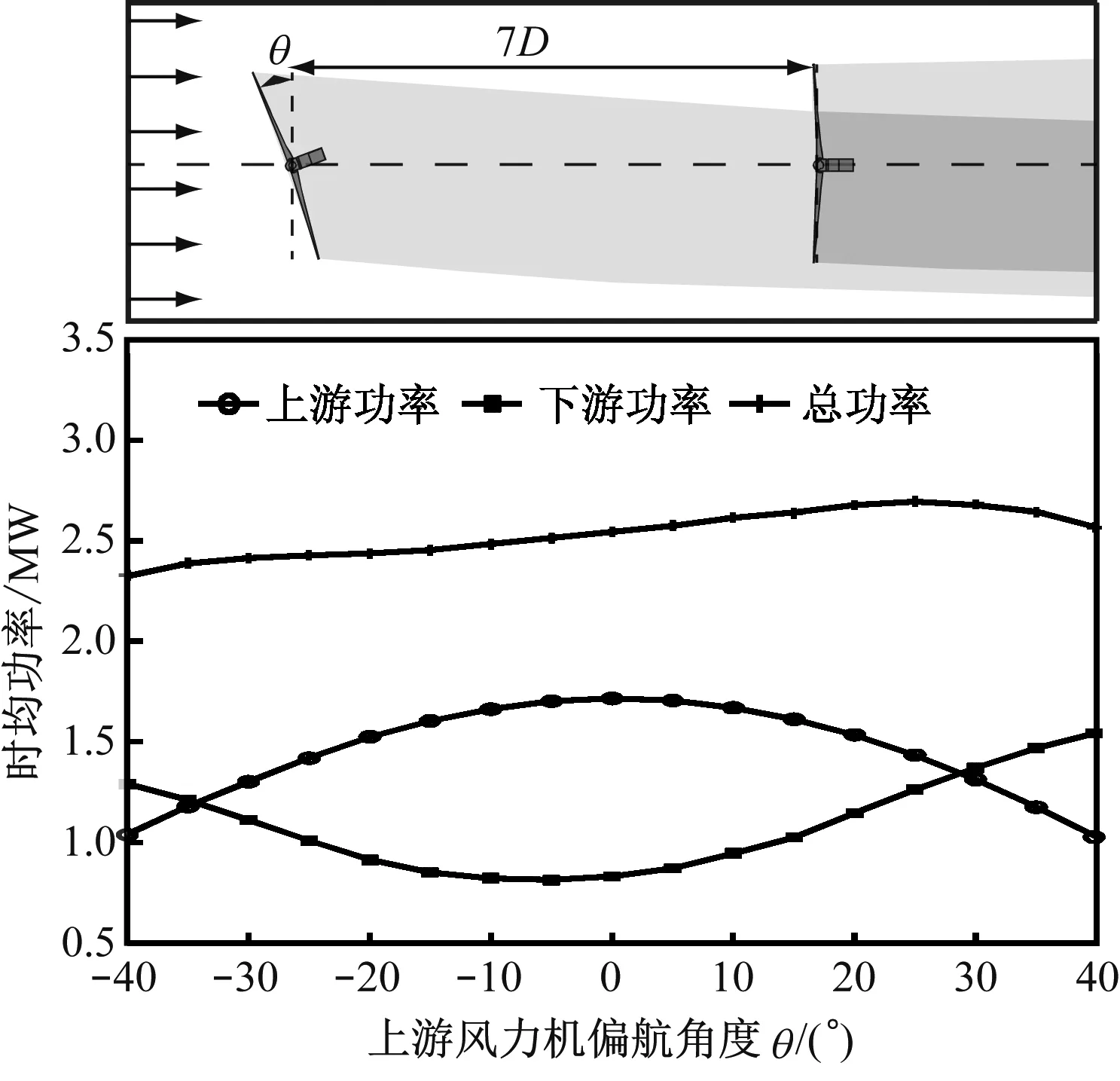
图2 上游风力机偏航角度对风场功率的影响
Fig.2 Influence of yaw angle of upstream wind turbine on the wind farm power output
1.3 计算域网格
模拟采用商用CFD软件STAR-CCM+10.02进行网格生成及流场计算.风场尺寸及网格细化分布如图3所示,由旋转域(2个风轮区域)和静止域(风场区域,包括塔架及机舱)组成,静止域使用结构化六面体网格,旋转域使用多面体网格以捕捉复杂的三维叶片曲面并通过滑移网格技术实现风轮旋转.鉴于风场模拟的多尺度性,网格分区域进行逐级细化,如图3虚线所示.叶根涡及叶尖涡的网格质量对尾迹发展影响重大,若不同网格尺寸之间过渡过大易导致涡量耗散过快,因此在1D区域内对叶根涡及叶尖涡影响范围使用更小尺寸网格进行细化.风场及风轮叶片处的网格如图4所示,叶片表面覆盖棱柱层网格以保证壁面边界层流动模拟的准确性.

(a) 俯视图

(b) 截面A-A′
Fig.3 Dimensions of the wind farm and regions of the mesh refinement
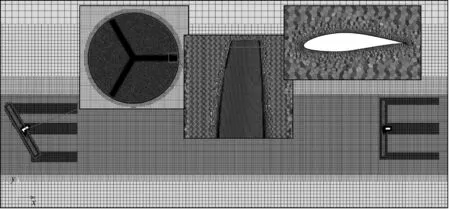
图4 风场及风轮网格拓扑
1.4 数值模拟设置
研究采用非定常不可压缩模拟方法,采用SSTk-ω湍流模型,采用隐式Segregated模型求解流动方程,压力-速度耦合采用SIMPLE算法,离散方程采用二阶迎风格式.入口边界为速度入口,出口边界为标准大气压(0 Pa)的压力出口,上侧及左右两侧边界使用对称平面以确保该表面没有法向速度和径向速度梯度的变化,风力机表面为光滑无滑移壁面,壁面y+值如图5所示.
对于地面,需使用粗糙的壁面条件以生成大气边界层环境.受大气边界层的影响,垂直方向的速度发生变化,接近地面处的风速有所降低,即所谓的风剪切效应[17].由于5 MW风力机的高度超过150 m,风剪切效应将影响风力机的运行状况[18],故不可忽略.


图5 壁面y+
(1)
(2)
式中:z为高度;κ为von Karman常数,κ=0.4;z0为大气粗糙高度;u*为摩擦速度;Cμ为与湍动能耗散相关的模型系数,Cμ=0.09;k为入口边界的湍动能,此处取固定值.
假设风场处于海上的中性大气边界层环境,故粗糙高度定义为0.001 m[8].通过STAR-CCM+的自定义函数将此风剪切速度应用于入口边界.通过SSTk-ω湍流模型生成的大气边界层实际为高雷诺数的壁面函数,速度需从边界层的对数律层开始发展,故地面边界网格的y+需大于30.地表的壁面函数为:
(3)
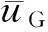
(4)
(5)
式中:kG为第一层网格的湍动能.对于地面边界条件的湍动能,定义为法向零梯度:
(6)
进行非定常模拟前,通过定常模拟赋予流场初值.额定风速下风轮的旋转周期为4.959 s,取时间步长为0.013 77 s,即每个时间步长风轮旋转1°.非定常模拟算例使用32个处理器并行进行,一个风轮旋转周期耗时近20 h.
2 计算结果及分析
2.1 网格及输出功率验证
通过定常模拟计算不同网格数下单个风力机的风轮扭矩,进行网格无关性验证,最终选取风场网格单元数约为2.42×107,其中每个风轮旋转区域的网格单元数为5.2×106,此时叶片表面最小尺寸为0.005 m,最大尺寸为0.05 m.
风力机的功率通过转子顺时针方向的扭矩估算:

(7)
式中:P为输出功率;M为转子扭矩;n为风轮转速.
从切入风速(3 m/s)至额定风速(11.4 m/s)进行定常模拟,计算上游风力机输出功率以验证模拟的准确性,结果示于图6.由图6可见,模拟结果与设计值相近,平均误差仅为6%.
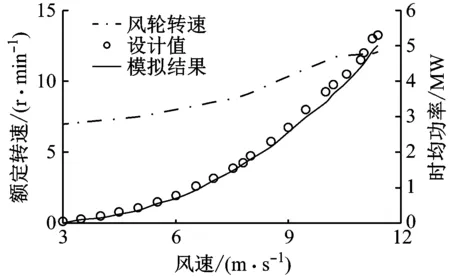
图6 输出功率验证
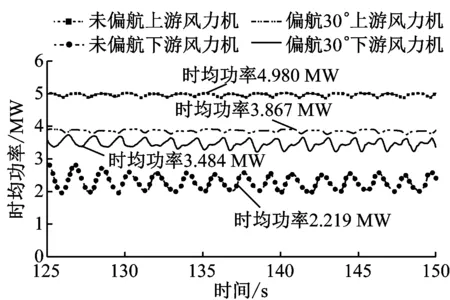
非定常计算以定常计算的结果为初始值,对应轮毂高度处风速为11.4 m/s的额定工况,风轮转速为12.1 r/min,计算过程中通过自定义函数监控入流风速大小,从而对风轮转速进行自动调整.图7为模拟150 s(约30个风轮旋转周期)偏航和未偏航情况下风力机的输出功率.偏航30°时上游风力机的功率下降22.35%,而下游风力机的输出功率增加57.01%,故上下游风力机总输出功率增加2.11%.
(a) 125~150 s功率曲线
(b) 2种工况风场平均功率对比
2.2 速度场分析
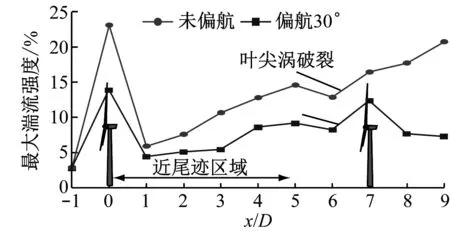
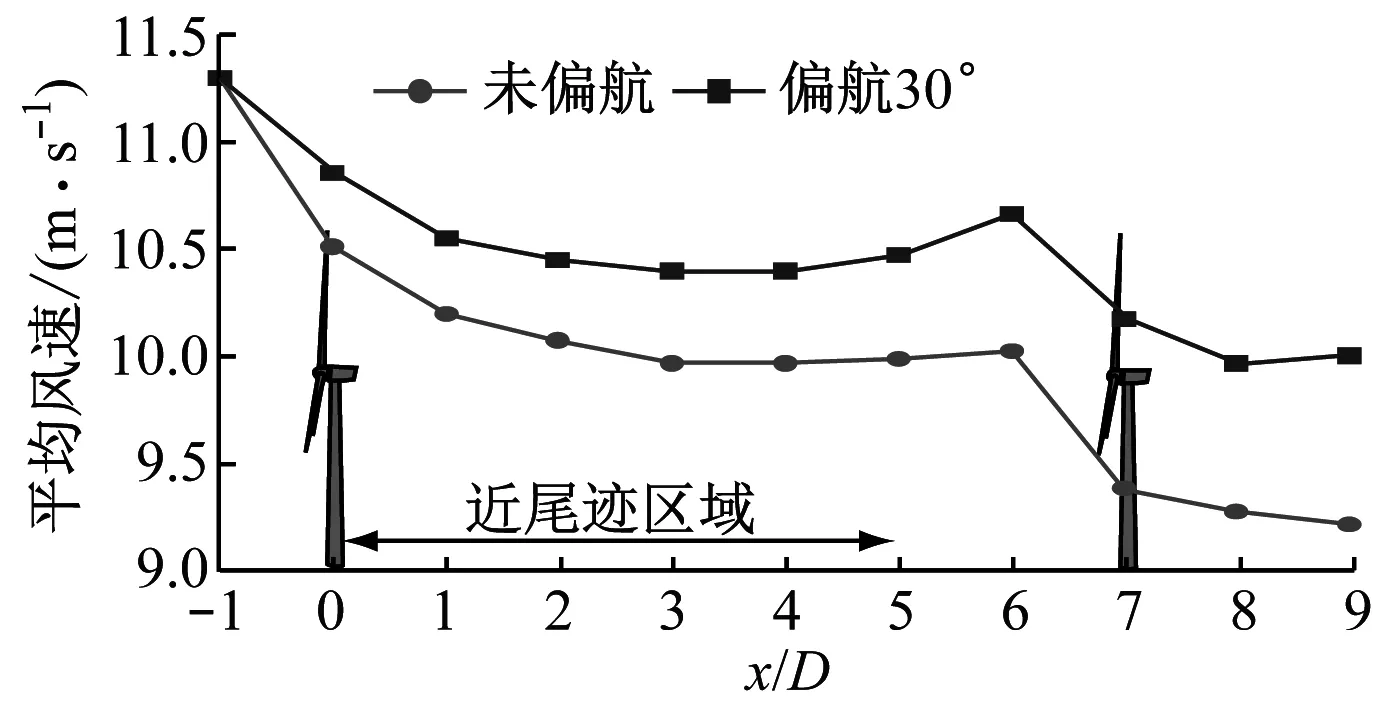
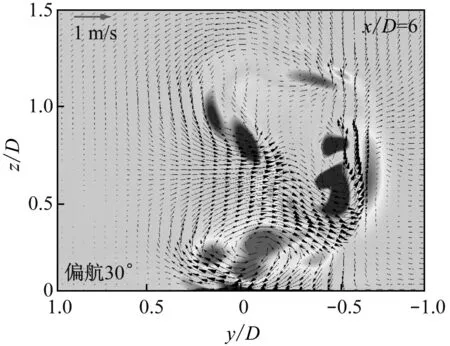
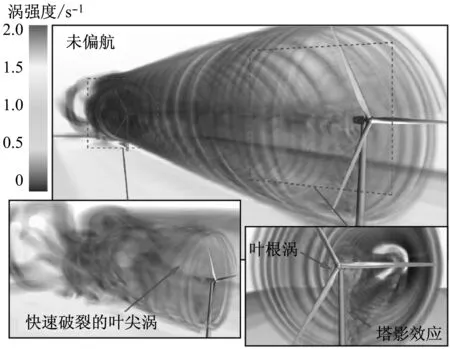
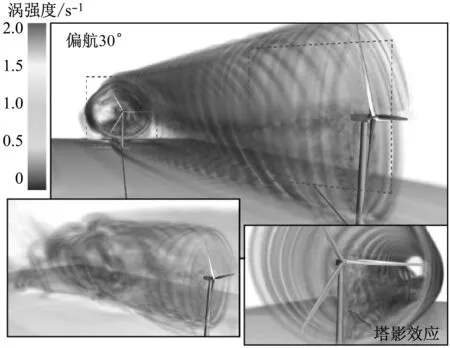
选取数个150 s时入流风向(x轴向)的垂直截面速度云图以及轮毂高度处的水平面速度云图,如图8所示.在x/D=0截面处可清楚观察到由塔影效应引起的低速区.当上游风力机未偏航时,0 当上游风力机偏航30°时,其尾迹形状不再具有对称性,并且随着传播距离的增加逐渐扭曲.通常在一些经验模型中(如WASP模型)尾迹被假设为具有对称性并以尾迹宽度表示其膨胀效应的程度[20].但当风轮偏航时,其尾迹将发生形变,低速区向上下方转移,导致传统的尾迹宽度定义方法可能难以真实地描述偏航尾迹的影响范围. (a) 未偏航工况 (b) 偏航30°工况 (c) 水平截面速度云图 Fig.8 Velocity contours of the flow field and velocity profiles at hub height 由图8(c)可知,偏航30°时轮毂高度处的尾迹在到达下游风力机时横向偏移约0.5D,与文献[8]的结果吻合.研究表明,由于旋转的尾迹与粗糙地面相互作用,当上游风力机未偏航时,其尾迹也将产生微小的横向移动距离[8].此时尾迹类似于一个逆时针旋转的漩涡,接近地面的低速风被尾迹向上卷起并向右上方移动,而高海拔的高速风被卷入至左下方.故尾迹左侧的速度亏损由高速风补充,从宏观上表现为尾迹向右移动.而偏航的尾迹流动结构更复杂. 2.3 尾迹流动结构分析 通常在尾迹影响范围内湍流强度将大幅度增加,当增加的湍流强度开始出现衰退时可认为该处叶尖涡发生破裂,衰退前区域定义为近尾迹区域[21].图9给出了各截面的最大湍流强度值和轮毂高度处的平均风速,其中湍流强度T由下式定义: (8) (9) 式中:u′为湍流速度脉动的均方根;U为平均速度(雷诺平均). 由图9可见,上游风力机偏航30°时尾迹的湍流强度总体较小.受叶片的影响,x/D=0截面处湍流强度陡升;当空气脱离叶片后,湍流强度降低;随后由于叶尖涡的发展,尾迹中的湍流强度随传播距离的增大而增加,在x/D=5至x/D=6区域开始衰退,故尾迹中的叶尖涡可能在此处发生较大规模的分解破裂.由图9(b)可见,x/D=5截面轮毂高度处的平均速度开始恢复,且在偏航工况下更为显著.因此可着重观察x/D=5与x/D=6两个截面的流动结构. (a) 最大湍流强度 (b) 平均风速 Fig.9 Maximum turbulence intensity of each section and the average speed 图10给出了不同截面x轴方向的瞬时涡量云图.由图10可见,在未偏航工况下上游风力机叶尖处产生一个环形结构的涡(即叶尖涡),随着尾迹的传播,该叶尖涡逐渐不稳定并在x/D=5截面开始消散.然而,当上游风力机处于偏航工况时,叶尖涡的结构及传播方式则完全不同,其形状变为近似椭圆而非圆形,并且随着传播距离的增加逐渐扭曲并分解为多个部分.此外,由于叶根涡及机舱的影响,尾迹的中心区域产生一个范围较大的涡,在未偏航时该中心涡较为稳定,但当上游风力机偏航时,该中心涡迅速分解并移动至右侧. 将未偏航工况与偏航工况下x/D=5与x/D=6截面的x轴向涡量与垂直流向(y和z方向)的速度矢量相叠加,结果示于图10,箭头长度代表速度矢量值的大小,箭头方向表示空气在该平面上的流动方向. 由图10可见,偏航工况下叶尖涡的径向速度相对较大,在其尾迹的左侧叶尖涡分解为一对反方向旋转的涡.高处的涡逆时针旋转而低处的涡顺时针旋转,因此左侧速度较高的风被该涡对卷入至尾迹,从而补偿了轮毂高度处的速度亏损.但也由于该涡对的旋转效应,更高及更低海拔处的速度亏损并未发生较明显的恢复. 为更好地观察尾迹中的涡量发展,图11给出了涡量绝对值在3维空间上的可视化,通过色彩处理过滤最小值以凸显由风力机产生的涡结构.由俯视图可见,在偏航工况下由叶根和机舱产生的中心涡被推向至右侧(从上游方向观察),并最终与叶尖涡混合,使得尾迹右侧的偏移不如左侧显著.从右视图可见,由于受到风剪切的影响,高海拔处的尾迹传播速度相对较快,导致叶尖涡在传播过程中逐渐倾斜,从而使得x方向涡量在截面上呈现正负方向混合状态.最下方的叶尖涡显示,偏航工况下的塔影效应相比于未偏航工况更为显著,该处的叶尖涡在更短的距离内分解破裂. 当尾迹传播至下游风力机区域时,下游风力机产生的尾迹叶尖涡受到上游冲击而难以保持正常的环形结构,在短距离内发生溃散.偏航工况时下游风力机左侧的叶尖涡相对更加稳定并且传播距离相对更远,但仍在2D距离内分解.因此,尽管上游风力机30°的偏航能使尾迹部分偏离下游风力机从而增加功率,但风速不均匀且湍流强度增加的尾迹可能使下游风力机的载荷波动剧烈,增加疲劳破坏的风险.此外,如果风场中风力机多于2排且上游的尾迹具有部分重叠效应,需谨慎考虑此无序混乱的重叠尾迹对更后排风力机的影响. (a) 各截面x轴向涡量 (b) x/D=5截面涡量及速度矢量 (c) x/D=6截面涡量及速度矢量 Fig.10 Distribution ofx-vorticity and the velocity vectors parallel to vertical sections (a) 未偏航工况3D涡量 (b) 偏航30°工况3D涡量 (c) 3D涡量局部细节 (1) 尾迹控制方法可有效提高风场总功率,上游风力机偏航30°时下游风力机输出功率提高57.01%,从而补偿上游风力机因有意偏航造成的功率损失,总功率提升2.11%. (2) 由风场速度云图可知,偏航30°时尾迹中心将横向偏移约0.5D,但此时生成的尾迹随传播距离的增加逐渐扭曲,流动结构发生变化而难以保持正常状况下的圆形尾迹. (3) 偏航工况下尾迹的湍流强度和速度亏损均有所降低.其叶尖涡随传播距离增加并且在左侧逐渐分离为一对逆时针旋转的涡,导致左侧尾迹外的空气被卷入至尾迹中,从而宏观上表现为轮毂高度处的速度亏损有明显恢复,但也由于该涡对的存在,偏航时上侧和右侧的尾迹未产生显著的横向位移. [1] HAU E. Wind turbines: fundamentals, technologies, application, economics[M]. 3rd ed. Berlin Heidelberg:Springer-Verlag, 2013. [2] CHOWDHURY S, ZHANG J, MESSAC A, et al. Optimizing the arrangement and the selection of turbines for wind farms subject to varying wind conditions[J]. Renewable Energy, 2013, 52: 273-282. [3] CHOWDHURY S, ZHANG J, MESSAC A, et al. Unrestricted wind farm layout optimization (UWFLO): investigating key factors influencing the maximum power generation[J]. Renewable Energy, 2012, 38(1): 16-30. [4] CHEN Y, LI H, JIN K, et al. Wind farm layout optimization using genetic algorithm with different hub height wind turbines[J]. Energy Conversion and Management, 2013, 70: 56-65. [6] WAGENAAR J W, MACHIELSE L A H, SCHEPERS J G. Controlling wind in ECN’s scaled wind farm[C]∥Proceedings of Europe Premier Wind Energy Event.Copenhagen, Denmark: EWEA, 2012. [7] ANDRESEN B. Wake behind a wind turbine operating in yaw[D]. Norway: Norwegian University of Science and Technology, 2013. [8] FLEMING P A, GEBRAAD P M O, LEE S, et al. Evaluating techniques for redirecting turbine wakes using SOWFA[J]. Renewable Energy, 2014, 70: 211-218. [9] FLEMING P, GEBRAAD P, LEE S, et al. High-fidelity simulation comparison of wake mitigation control strategies for a two-turbine case[C]∥Proceedings of the International Conference on Aerodynamics of Offshore Wind Energy Systems and Wakes. Lyngby, Denmark,USA: ICOWES, 2013. [10] 王强. 水平轴风力机三维空气动力学计算模型研究[D]. 北京: 中国科学院研究生院(工程热物理研究所), 2014. [11] LYNCH C E, PROSSER D T, SMITH M J. An efficient actuating blade model for unsteady rotating system wake simulations[J]. Computers & Fluids, 2014, 92: 138-150. [12] KIM T, OH S, YEE K. Improved actuator surface method for wind turbine application[J]. Renewable Energy, 2015, 76: 16-26. [13] WILSON J M, DAVIS C J, VENAYAGAMOORTHY S K, et al. Comparisons of horizontal-axis wind turbine wake interaction models[J]. Journal of Solar Energy Engineering, 2015, 137(3): 031001. [14] JONKMAN JM, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[M]. Golden, CO: National Renewable Energy Laboratory, 2009. [16] CHOI N J, NAM S H, JEONG J H, et al. Numerical study on the horizontal axis turbines arrangement in a wind farm: effect of separation distance on the turbine aerodynamic power output[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 117: 11-17. [17] GORDER P J, KAUFMAN K, GREIF R. Effect of wind gradient on the trajectory synthesis algorithms of the Center-TRACON automation system (CTAS)[C]∥AIAA, Guidance, Navigation and Control Conference.San Diego, CA: AIAA,1996. [18] PORTÉ-AGEL F, WU Y T, LU H, et al. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(4): 154-168. [19] RICHARDS P J, NORRIS S E. Appropriate boundary conditions for computational wind engineering models revisited[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(4): 257-266. [20] MO J O, CHOUDHRY A, ARJOMANDI M, et al. Large eddy simulation of the wind turbine wake characteristics in the numerical wind tunnel model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 112: 11-24. [21] SCHÜMANN H, PIERELLA F, SAETRAN L. Experimental investigation of wind turbine wakes in the wind tunnel[J]. Energy Procedia, 2013, 35: 285-296. Investigation on Flow Mechanism of a Wind Farm Based on Yawed Wind Turbine Using Wake Deflection Control Strategy MIAOWeipao1,LIChun1,2,YANGJun1,2 (1. School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China) To study the flow mechanism of a wind farm based on yawed wind turbine using wake deflection control strategy by multi-scale simulation, two full-scale 5 MW wind turbines laid in line were simulated in the atmospheric boundary layer environment through unsteady CFD method. Results show that the total power generation of wind farm can be increased by intentionally yawing the upstream wind turbine. According to the analysis of velocity field, the wake of upstream wind turbine would deform when the turbine is placed yawingly, and according to the analysis of vorticity field, a counter-rotating vortex pair would be observed as the yawed wake propagates, which would lead to the macroscopic wake deflection. However, the wake deviation effect is significant just at the hub height. The distorted wake still spreads its low speed regions to other areas. wake control; yaw; horizontal axis wind turbine; blade tip vortex; CFD 1674-7607(2017)08-0655-08 TK83 A 480.60 2017-06-19 国家自然科学基金资助项目(51176129);上海市科委资助项目(13DZ2260900) 缪维跑(1990-),男,浙江苍南人,博士研究生,主要从事风力机方面的研究.电话(Tel.):13122369396; E-mail:mwpusst@163.com.
















3 结 论

