基于频响函数法的曲轴轴系扭振分析与控制

郭军丽，苏章明，陈寒霜，邢维者，徐仰汇

(广州汽车集团 汽车工程研究院，广州 511434)

基于频响函数法的曲轴轴系扭振分析与控制

郭军丽，苏章明，陈寒霜，邢维者，徐仰汇

(广州汽车集团 汽车工程研究院，广州 511434)

基于原点频响函数法对曲轴轴系匹配三种不同TVD时的扭振进行计算，可以快速预测TVD减振效果。首先引入扭转减振器减振原理；其次介绍集总参数有限元法计算扭振的方法；然后通过扭转模态识别曲轴轴系的模态频率，通过频响函数结果判别曲轴轴系在单位激励力矩作用下扭振幅值的大小；最后，试验测试曲轴安装TVD位置处的扭振加速度，并和仿真进行对比。结果发现，频响函数法计算的扭振幅值曲线和测试结果趋势相同，且对这三种TVD降低车内噪声的效果进行了比较。

振动与波；频响法；TVD；扭振；有限元；扭转加速度

曲轴轴系是指发动机曲轴和与之相连的各运动部件的总成，是典型的扭振系统。强烈的扭振会通过传动系统传递到车内，形成主观感受不能接受的声音，比如轰鸣声、异响（“咕噜”）声等，因此曲轴轴系中匹配的扭转减振器（TVD)减振性能的好坏，直接影响整车NVH性能。匹配合适的扭转减振器，可降低轴系扭振幅值，有效避免曲轴因扭振过大造成的疲劳断裂，还可降低车内噪声及异响。

为了快速预测TVD减小曲轴轴系扭振的效果，采用原点频响函数法计算单位力矩激励下曲轴扭转幅值，借助三维有限元对匹配不同TVD的曲轴轴系进行建模仿真，识别曲轴扭转模态频率及频响函数曲线，最后和试验结果进行对比，把单位力矩激励作用下曲轴扭转加速度仿真曲线和试验中实际激励下曲轴安装扭转减振器后的扭转加速度曲线进行对比，发现两者趋势基本一致。

1 扭转减振器减振原理

结合工程实际中常见的单级扭转减振器对原理作简单介绍，图1所示为曲轴加装单级扭转减振器后的等效力学模型。

图1 曲轴系统和扭转减振器的等效力学模型

其中Jeq、keq和ceq分别为曲轴等效系统的转动惯量、扭转刚度和阻尼系数，J0、k0和c0分别为扭转减振器惯性质量的转动惯量、橡胶元件的扭转刚度和阻尼系数，则整个系统相当于两自由度扭转振动系统。

根据牛顿第二定律，建立运动微分方程

则频响函数中的第一行、第一列即为扭转减振器安装位置的原点频响函数

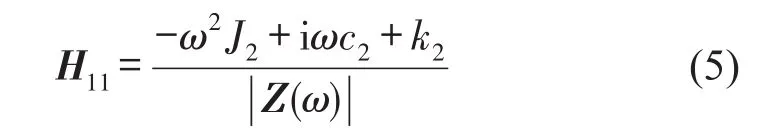
该函数中的变量包括主系统的惯量Jeq、阻尼ceq、刚度keq、扭转减振器的惯量J0、阻尼c0、刚度k0。优化的目的是使得频响函数值最小，即单位力矩激励下，扭转幅值最小。

当扭转减振器安装位置点外的主系统频响函数值最小时，便可获得最优的频率比、惯量比以及阻尼比。因而可通过调节这些参数来优化扭转减振器。

2 集总参数三维有限元建模

曲轴轴系扭振系统是指曲轴和参与曲轴一起运动的有关机件（如活塞、连杆、飞轮、齿轮、皮带轮、平衡轴等）的总称。它们都是连续的体系，具有复杂的几何形状。有些机件并不是做简单的旋转运动（如活塞、连杆），为了便于研究，一般在能保证计算精度的前提下把复杂的系统进行简化：将非旋转运动简化为旋转运动，将连续分布体系的当量惯量由集中转动惯量代替。

2.1 等效转动惯量计算

采用集总参数有限元方法建模，其中重点考虑活塞连杆机构和平衡轴齿的等效转动惯量。下面分别介绍活塞连杆机构和平衡轴齿等效转动惯量的计算。

活塞连杆的等效转动惯量分为两部分，一部分为往复运动部分的转动惯量，另一部分为旋转质量的转动惯量。

(1)往复运动部分惯量的简化，即将连杆的质量简化为集中于连杆小头的质量mA和集中于连杆大头的质量mB[4]，如图2所示。

图2 连杆的等效质量系统

连杆小头的质量和活塞、活塞环等一起只沿活塞运动方向做往复直线运动，而连杆大头的质量只是绕曲轴做圆周运动。假设连杆质量为ml，则mA、mB按下列原则确定[3]

上式中L为连杆长度，L1为连杆小头到连杆质心的距离，L2为连杆大头到连杆质心的距离。

根据动能等效原则，连杆及活塞的等效转动惯量为[2]

其中r为曲柄半径；mr为旋转质量（即连杆大头的质量mB)；ma为往复惯性质量（即连杆小头的质量mA及活塞组件的质量mp之和）。

（2）旋转质量的转动惯量简化，即平衡轴齿的等效转动惯量计算。

图3 曲轴及平衡轴示意图

设曲轴转动惯量为J1,转角为ω1，平衡轴1的转动惯量为J2,转角为ω2，平衡轴2的转动惯量为J3,转角为ω3，平衡轴1与平衡轴2惯量等效为曲轴的当量转动惯量为J23，根据动能守恒，可得

2.2 三维有限元建模

根据2.1小节中介绍的等效转动惯量计算方法，以某车型曲轴轴系为例，计算可得等效到曲轴上的四个活塞连杆机构的当量惯量是5.4 t ∙mm2，平衡轴等效到曲轴上的转动惯量是5.656 t ∙mm2，然后建立曲轴轴系三维有限元模型，某个曲轴轴系集中参数三维有限元模型如图4所示。

2.3 扭转频响函数计算

由于曲轴轴系自由端即安装扭转减振器的位置扭转幅值最大，同时为了测试中工装方便，对该点的扭振进行测试。因此以该点作为基本参考点计算原点扭转频响函数。

类似于平动原点频响函数法，扭转原点频响函数法是在参考点施加单位力矩，求解该点的扭转加速度响应，所得到的扭转加速度在频域变化的曲线即为扭转原点频响曲线。

通过频响函数即可识别曲轴扭转模态频率。由于曲轴实际中主要受周期力矩的激励，所以可用频响函数的峰值趋势和试验结果进行对比。

图4 曲轴轴系集中参数三维有限元模型示例

3 匹配三种TVD的某曲轴仿真计算

图5所示为三种不同TVD实物图。

图5 三种不同TVD实物图

通过仿真计算分别得到该曲轴系匹配三种TVD时的扭转振型，如图6、图7、图8所示。

图6 轴系匹配1号TVD时的扭转模态（403 Hz)

图7 轴系匹配2号TVD时的扭转模态(352 Hz)

图8 轴系匹配3号TVD时的扭转模态(278 Hz)

根据2.2小节中阐述的方法，曲轴轴系匹配这三种TVD时的频响曲线如图9所示。

由于问题频率在200 Hz以上，因此把200 Hz以上扭振出现的第一个峰值对应的频率称为曲轴1阶扭转频率，依次类推。通过仿真得到的频响曲线可以看到，匹配3号TVD时曲轴轴系的1阶扭转幅值最低，2号其次，1号最高。TVD即扭转减振器的主要作用就是降低曲轴的扭转幅值，从而降低曲轴轴系在激励源作用下的响应幅值，因此，可以发现这三种TVD中，3号TVD降低扭转幅值的效果最好。下文通过试验进行验证。

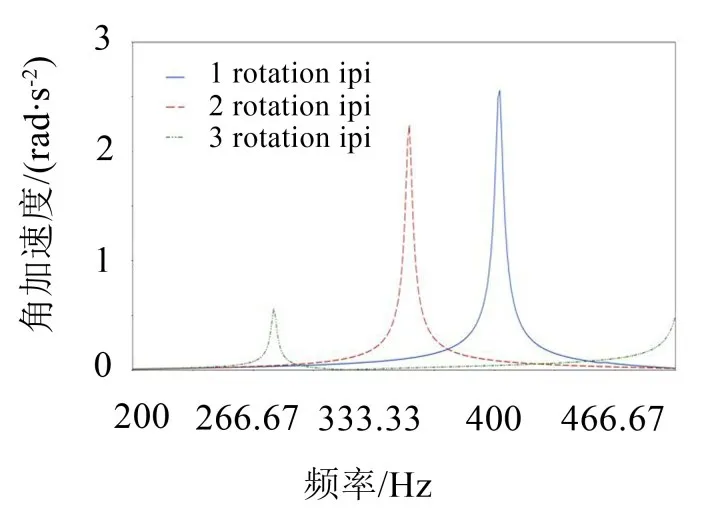
图9 曲轴匹配三种TVD时1阶扭转振动原点频响曲线

4 试验验证

4.1 扭振测试

如图10所示，分别安装上述3种TVD在整车上进行扭振测试和分析。

图10 TVD安装在整车上时的扭振测试

测试中发动机最高转速为5 000 r/min，且整车在8谐次激励下时，车内异响声相对比较明显，因此给出8谐次下的曲轴扭转加速度曲线，如图11所示。

图中加速度曲线峰值如虚线箭头所示。可以发现，测试所得到的曲轴扭振加速度曲线峰值的变化规律（相对大小）和仿真结果基本一致，匹配2号TVD时频响幅值略有变化。匹配1号TVD时曲轴1阶扭转幅值最大，匹配2号时其次，匹配3号TVD时最小(1阶峰值转速约为2 250 r/min）。曲轴1阶扭转频率试验结果计算如式(10)所示。

式中n为转速，m为谐次，例如1号TVD曲轴转速约为3 100 r/min，则测试频率即为410 Hz。

图11 8阶次激励下扭振加速度曲线

仿真结果和试验结果对比如表1所示。

从表中可以看到，仿真1阶频率误差最大不超过10%，说明该建模方法对于曲轴轴系的扭振频率及扭转频响分析基本可靠。

4.2 车内噪声测试

首先确定车内异响声音的频率。通过滤波发现，若滤掉中心频率为400 Hz的声音，车内异响声明显降低。然后分别对匹配这三种TVD时车内异响控制效果进行确认测试，分析车内异响声的改善效果。结果如图12、图13、图14所示。

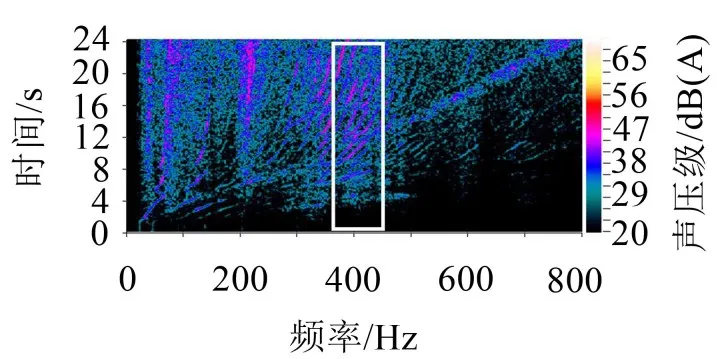
图12 1号TVD对应的车内噪声Colourmap图

图13 2号TVD对应的车内噪声Colourmap图

从图12至图14可以看到，3号TVD有效降低了400 Hz附近存在的异响声，与仿真结论一致，从而实车采用3号TVD来控制车内异响声。

表1 曲轴1阶扭转频率仿真结果与试验结果对比

图14 3号TVD对应车内噪声Colourmap图

5 结语

首先对（单级）二自由度扭转减振器的原理进行分析介绍；接着介绍集总参数有限元方法分析扭振的具体建模方法；然后使用该建模方法对曲轴轴系匹配三种不同TVD后的扭转原点频响曲线进行仿真分析，并通过比较找出最优的TVD；最后，通过对匹配三种不同TVD时的实车车内噪声进行对比，验证仿真分析结果的准确性。结论如下：

（1）扭转减振器外环惯量越大，曲轴系统1阶扭振幅值越小。

（2）用提出的集总参数建模方法分析扭振频率及频响准确可靠。

（3）能有效解决车内异响问题的惯量环为3号惯量环。

[1]背户一登，任明章.动力吸振器及其应用[M].北京：机械工业出版社，2013.

[2]杨连生.内燃机设计[M].吉林：中国农业机械出版社，1981.

[3]陆际清，孟嗣宗.汽车发动机设计[M].北京：北京清华大学出版社，1989：134-176.

[4]陈超.汽车发动机曲轴系统扭转振动分析与减振器匹配的研究[J].机械传动，2012，36(2)：53-56.

[5]王祺.内燃机轴系扭转振动[M].大连：大连理工大学出版社，1991：136-143.

[6]上官文斌，杨明生，李耀龙.汽车发动机曲轴减振[J].现代零部件，2007：68-69.

[7]庞剑，谌刚，何华.汽车振动与噪声[M].北京：北京理工大学出版社，2006.

[8]朱孟华.柴油机装置扭转振动减振器的设计计算[J].上海交通大学学报，1980(1)：119-133.

[9]吕振华，冯振东.汽车发动机曲轴阻尼式扭振吸振器设计方法探讨及应用[J].内燃机工程，1992，13(3)：27-33.

[10]上官文斌.发动机曲轴系统扭转振动建模与实测分析[J].测试与诊断，2012.

[11]IWANAMI K.SETO K.An optimum design method for the dual dynamic damper and its effectiveness[J].JSME,1984,27(231):1965-1973.

[12]XU Z C,ANDERSON R J.A new method for estimating amplitudes of torsional vibration for engine crankshafts[J].International Journal of Vehicle Design,1988,9(2):252-261.

[13]郝志勇，舒歌群，史绍熙.内燃机轴系扭振响应的扭转弹性波计算方法研究[J].内燃机学报，2000，18(1)：29-32.

[14]谌刚，陈之炎，李良风.具有变惯量的柴油机曲轴系统扭转振动[J].内燃机学报，1991，9(2)：143-149.

Analysis and Control of Crankshaft Torsional Vibration Based on Frequency Response Functions

GUO Jun-li,SU Zhang-ming,CHEN Han-shuang,XING Wei-zhe,XU Yang-hui
(Automotive Engineering Research Institute,Guang ZhouAutomobile Group,Guangzhou 511434,China)

The torsional vibrations of a crankshaft with three different TVDs are computed based on the origin frequency response function method.This method can quickly predict TVD damping effect.First of all,the torsional vibration damping principle is elaborated and the finite element method for torsional vibration computation based on the integrated parameters is introduced.Then,the modal frequencies of the crankshaft are identified through the torsional modals.And the amplitudes of the torsional vibration of the crankshaft system under the unit torque excitation are distinguished based on the results of the frequency response function.Finally,the torsional vibration acceleration of the crankshaft located in TVD is tested and compared with the simulation results.It is found that the curves of the torsional vibration amplitude by frequency response function method and by the testing are consistent.Furthermore,the interior noise reduction effects of the three kinds of TVD are summarized.

vibration and wave;frequency response function;torsional vibration damper;torsional vibration;finite element;torsional acceleration

TB535；TB53

：A

：10.3969/j.issn.1006-1355.2017.04.042

1006-1355(2017)04-0209-05

2016-10-14

郭军丽（1987－），女，陕西省扶风县人，NVH仿真工程师。主要研究方向为汽车动力总成NVH分析。

E-mail:guojie173@163.com