环境激励下Karhunen-Loève变换与模态分解间的关系

宋贤云，宋汉文

（同济大学 航空航天与力学学院，上海 200092）

环境激励下Karhunen-Loève变换与模态分解间的关系

宋贤云，宋汉文

（同济大学 航空航天与力学学院，上海 200092）

Karhunen-Loève（KL）变换作为一种基于相关函数的最佳变换，在振动分析领域已经受到广泛关注。然而，该方法还缺乏清晰完整的模态解释。在空间几何上，振动分析中模态分解是振动响应信号在由振型构成的基底上的展开，KL变换是信号在由一组正交KL特征向量构成的空间中的投影过程。对环境激励下响应的KL变换与模态分解进行类比，探讨两者间的关系。结果表明：KL特征向量收敛于质量信息加权后的振型；KL特征值表征各阶模态的能量参与度；KL变换系数收敛于模态坐标。最后，通过仿真计算验证分析结论的正确性。

振动与波；Karhunen-Loève变换；模态分解；环境激励

Karhunen-Loève（KL）变换是一种从信号中提取正交基（或特征函数，也称KL特征向量）以进行模型分解的过程。KL变换具有如下特性[1]：

(1)去相关性。信号进行KL变换后，各分解量互不相关。

(2)能量集中性。对N＞1维矢量信号进行KL变换后，较大的方差集中在前M（0＜M＜N）项分解量。

(3)最佳特性。KL变换是在均方误差测度下重构失真最小的一种方法，其重构误差为被略去的各KL分解量之和。基于这些特性，KL变换方法已经被成功地应用于流体动力学[2]、热分析[3]、故障诊断[4]等学科中的模型降阶以及响应的重构。在结构动力分析和系统辨识领域，已论证KL变换可用于获得精确的低阶动力模型[5]。相比传统Galerkin或Rayleigh-Ritz方法，利用KL变换可用更少的模态来获取相同的能量[6]。从这一方面看，KL变换获得的模态是最佳的。

从结构动力学中的应用意义角度考虑，讨论KL变换的各参量（KL特征向量、KL特征值、KL变换系数）与结构模态间的关系是十分有必要的。文献[7]指出，在质量均匀分布的离散系统中，若总体数据量足够大，利用KL变换从数字仿真数据中提取的特征向量收敛于振动正则模态，并且特征值与数据中的能量分布有关。

随着振动分析领域不断发展，环境激励下模态分析的理论以及应用也日益丰富[8–11]。KL变换作为一种有效的数据分析方法，目前该方法还缺乏清晰完整的模态解释。环境激励通常假设为白噪声，文中也在这一前提下进行讨论。首先对KL变换理论进行介绍，通过与模态分解进行类比，对KL变换的各参量：KL特征向量、KL特征值和KL变换系数，进行了模态解释。最后通过仿真结果验证解释的合理性。

1 Karhunen-Loève变换

由此，{u(t)}有表达式

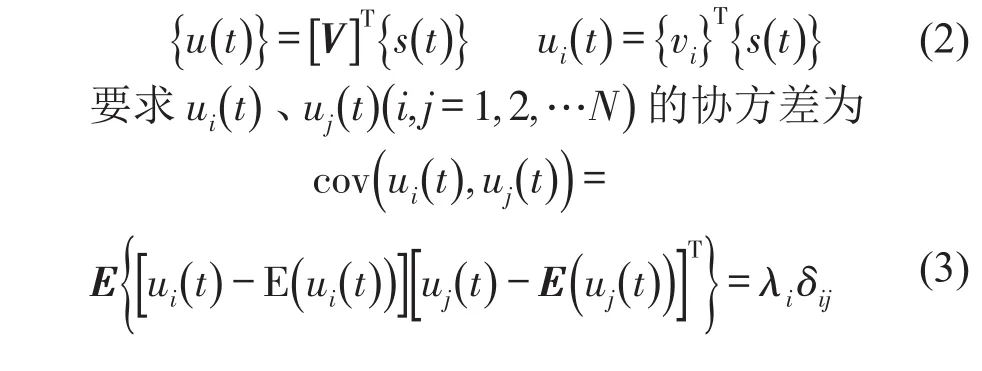
式(4)写成矩阵形式

综上所述，式(1)即为Karhunen-Loève变换，称为KL特征向量或KL基，λi称为KL特征值。

2 Karhunen-Loève变换与模态分解的关系

N自由度线性时不变离散系统的动力学方程为[12]

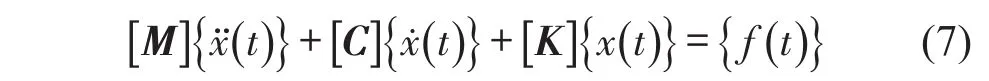
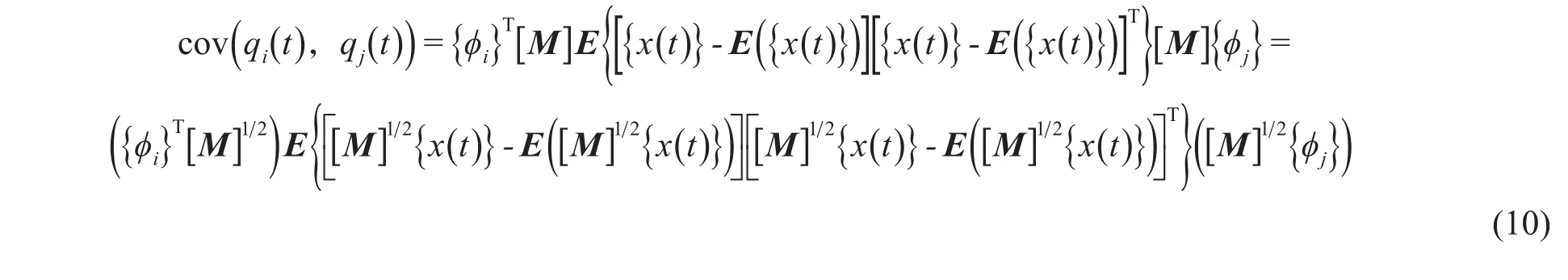
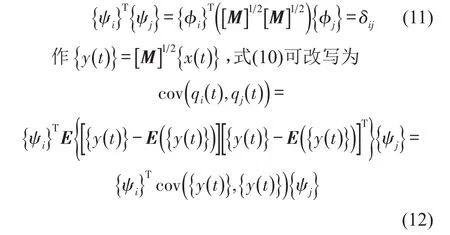
假设系统承受白噪声激励是零均值的，根据NExT理论[13]，式(12)可进一步写为

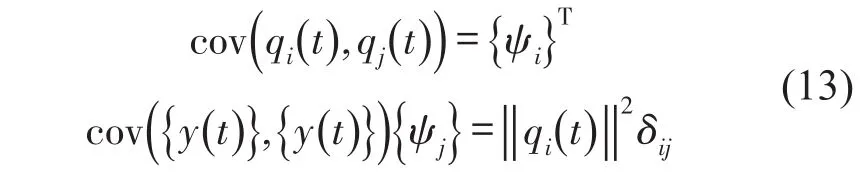
比较式(4)和式(5)，可以得出结论：对于正交向量{ψi}，常数的KL特征向量和KL特征值。写成KL变换形式

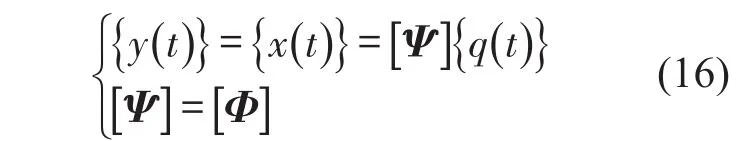
综上所述，环境激励下，KL变换在振动分析中的模态意义在于：对于已知系统质量矩阵，对系统响应线性变换后，进行KL变换就能够获得系统按能量贡献度排列的模态振型、模态坐标。

3 仿真验证

为验证文中对环境激励下KL变换与模态分解间关系的解释，建立三自由度质量弹簧振动系统仿真模型（见图1）。

图1 三自由度质量弹簧振动系统

图1中，质量矩阵为

刚度矩阵为

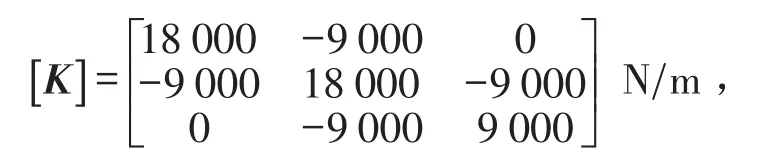
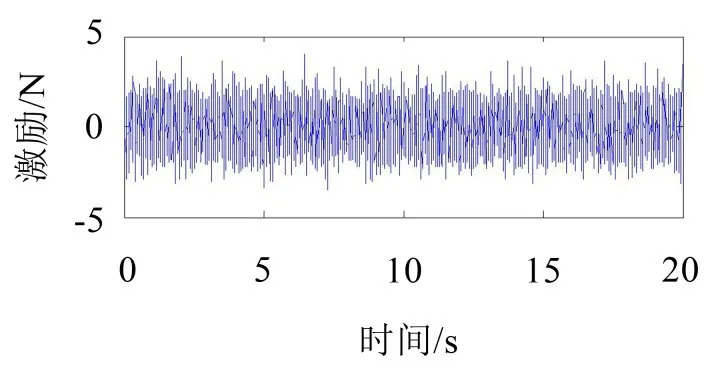
图2 激励信号

图3 位移响应信号

图4 KL变换计算向量{i}与模态振型向量{ϕi}比较 (图中虚线表示向量{ϕi}，实线表示向量{i})

比较KL特征值λi与系统能量参与因子并计算两者间相对误差

结果见表1。从中可知，KL特征值λi与能量参与因子是近似相等的，这就验证了式(13)。

4 结语

对KL变换与振动分析中的模态分解进行类比，探讨两者的关系。模态分解和KL变换在空间几何上具有共有特性：皆是一组信号在正交向量（或线性无关的向量）构成基底上的展开过程。对已知质量的线性离散系统进行分析，结果表明：环境激励下，KL特征向量收敛于质量信息加权后的振型；KL特征值表征模态振型的能量参与度；KL变换系数收敛于系统的模态坐标。最后，通过仿真计算验证了分析结论的正确性。这就为后续KL变换在系统工况模态辨识以及健康监测与精确控制中的应用提供了理论依据。

表1 能量参与因子‖qi(t)‖2与KL特征值λi比较 (单位：1)

图5 模态坐标qi(t)(i=1,2,3) 与KL变换系数的比较

[1]GHANEM R G,SPANOS P D.Stochastic finite element:a spectral approach[M].New York:Springer,1991:20-45.

[2]SIROVICH L.Turbulence and the dynamics of coherent structures part I:coherent structures[J].Quarterly of Applied Mathematics,1986,45(3):561-571.

[3]PARK H M,CHO D H.The use of the Karhunen-Loève decomposition for the modeling of distributed parameter systems[J].Chemical Engineering Science,1996,51(1):81-98.

[4]JOYNER M L,BANKS H T,WINCHESKI B,et al.Nondestructive evaluation using a reduced order computational methodology[J].Inverse Problems,2000,16(4):929-945.

[5]GEORGIOU I T,SCHWARTZ I B.Dynamics of large scale coupled structural mechanical systems:a singular perturbation proper orthogonal decomposition approach[J].Siam Journal on Applied Mathematics,1999,59(4):1178-1207.

[6]SIROVICH L,KNIGHT B W,RODRIGUEZ J D.Optimal low-dimensional dynamical approximations[J].Quarterly ofApplied Mathematics,1990,48:535-548.

[7]FEENY B F,KAPPAGANTU R.On the physical interpretation of proper orthogonal modes in vibrations[J].Journal of Sound Vibration,1998,211(4):607-616.

[8]CARNE T G,JAMES G H I.The inception of OMA in the development of modal testing technology for wind turbines[J].Mechanical Systems and Signal Processing.2010,24(5SI):1213-1226.

[9]秦飞，宋汉文，王文亮.基于现代谱估计理论的工况模态分析[J].振动与冲击，2002，21(4)：74-79.

[10]周鋐，曹阳光，刘浩，等.汽车顶棚约束模态与工作模态分析与比较[J].噪声与振动控制，2016，36(2)：84-87.

[11]BRINCKER R.Some elements of operational modal analysis[J].Shock and Vibration，2014(4):1-11.

[12]傅志方.振动模态分析与参数辨识[M].北京：机械工业出版社，1990：161-267.

[13]JAMES III G H,CARNE T G,LAUFFER J P.The natural excitation technique (NExT) formodalparameter extraction from operating wind turbines[J].NASA STI/Recon Technical Report N,1993,93(4):260-277.

Relationship Between Karhunen-Loève Transformation and Modal Decomposition UnderAmbient Excitations

SONG Xian-yun,SONG Han-wen
(School ofAerospace Engineering andApplied Mechanics,Tongji University,Shanghai 200092,China)

As a best transformation based on the correlation function,Karhunen-Loève transformation(KLT)has been paid a wide attention in vibration analysis.However,this method lacks a clear and complete modal interpretation.In view of spatial geometry,the modal decomposition in vibration analysis is a procedure of expanding response signals on the bases of modal shapes,while KLT is a projection procedure of the signals in the space composed by orthogonal KL eigenvectors.This paper discusses the relationship between the KLT and the modal decomposition under ambient excitation.The results show that the KL eigenvectors are approximated to the weighted modal shapes,the KL eigenvalues represent the energy contribution of the corresponding modes,and the KL coefficients converge to the modal coordinate.Finally,conclusion of the analysis is verified by numerical simulation.

vibration and wave;Karhunen-Loève transformation;modal decomposition;ambient excitation

O321；O327

：A

：10.3969/j.issn.1006-1355.2017.04.001

1006-1355(2017)04-0001-04+46

2017-05-015

国家自然科学基金资助项目（11272235）

宋贤云（1987－），女，河南省鹤壁市人，博士研究生，主要研究方向为工况模态分析与模态参数辨识。

宋汉文，男，博士生导师。

E-mail:hwsong@tongji.edu.cn