基于载荷识别的辅助变流器柜体振动模型修正

丁 杰，张 平，王永胜，曾亚平，臧晓斌

（1.湘潭大学 土木工程与力学学院，湖南 湘潭 411105；

2.株洲南车时代电气股份有限公司 技术中心，湖南 株洲 412001）

基于载荷识别的辅助变流器柜体振动模型修正

丁 杰1,2，张 平1，王永胜2，曾亚平2，臧晓斌2

（1.湘潭大学 土木工程与力学学院，湖南 湘潭 411105；

2.株洲南车时代电气股份有限公司 技术中心，湖南 株洲 412001）

为提高某地铁车辆辅助变流器柜体振动响应模拟结果的精度，提出一种结合动载荷识别与优化算法的振动模型修正方法。首先在辅助变流器柜体有限元模型的基础上，计算出载荷与响应之间的传递函数，并利用振动响应测试数据和传递函数计算出施加在各测点的载荷谱。然后采用序列二次规划算法对有限元模型进行模型修正，通过构造目标函数将多输出模型修正问题转化为单输出模型修正问题。最后，对修正后的有限元模型进行振动响应求解，分析结果与振动测试数据比较验证了模型修正方法的正确性。该方法可为进一步实现辅助变流器柜体的减振降噪创造必要条件。

振动与波：载荷识别；模型修正；传递函数；矩阵求逆；优化算法

由于仿真技术的发展以及振动问题的复杂性，复杂系统振动问题解决除利用振动测试及数据分析外，已经越来越多地借助有限元方法进行数值模拟。建立复杂系统的有限元模型时，往往要进行很多简化且存在不确定性因素（如衬套刚度、螺栓连接刚度等参数），计算出的振动响应必然与实测振动响应存在较大误差，因此需要对有限元模型进行修正，以保证振动响应计算值满足误差要求。

由于受到试验条件的各种限制，复杂系统振动的激励源往往很难通过测试准确获取，而振动响应的测量很容易实现，因此载荷识别方法受到重视[1]。在复杂系统的振动计算中，利用载荷识别进行振动模型修正的方法主要有模态法和频响函数法[2–3]。模态法可以从试验特征值和特征向量来调整预测参数，然而无论是直接模态法还是迭代模态法，都存在振型匹配问题。频响函数法利用预测的和测量的频响函数对振动模型进行修正，克服了模态法需要振型一一对应的缺点，且修正计算可以在很宽的频率范围内进行[4–7]。

通过建立复杂系统的有限元模型可以获取振动传递函数，再利用矩阵求逆可以反推算出激励载荷。载荷识别与振动响应、模型修正之间存在不断的迭代，可以采用优化算法完成振动模型的修正过程。在识别出正确的载荷并对有限元模型进行修正的基础上，可以对复杂系统的振动进行深入的研究分析，如传递路径分析、模态贡献量分析等，找出引起振动的主要来源和主要模态，从而为减振降噪找到正确途径。

文中以某地铁车辆辅助变流器柜体为对象，通过反推算载荷与优化算法来修正有限元模型中的不确定性参数，使计算出的振动加速度逐步逼近实测的振动加速度，最终得到修正后的有限元模型和正确激励，通过仿真与试验的振动响应结果对比，验证了修正方法的合理性与正确性。

1 载荷识别和振动修正理论

1.1 多自由系统的振动

多自由度系统的动力学方程为

其中M、C和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵，M和K通常是对称矩阵，阻尼采用瑞利阻尼，C=αM+βK，{x}和{f}分别为系统的广义位移和广义力。

式（1）是耦合方程，可采用模态叠加法计算。模态的计算公式为

其中ω为角频率，{A}为振型。一个系统有n个自由度，即有n个ω2解和与之对应的n个{A}解。

模态有振型、质量矩阵和刚度矩阵这3个基本的正交性

由于{A}具有正交性，对于任意位移向量{x}，可以取

其中[Φ]是由模态向量{A}i构成的矩阵，{η}是由系数ηi构成的列向量，称为模态参与因子向量。

将式（6）代入式（1）可得到

式（7）两边同乘以[Φ]T，得到

从式（9）中解出ηi后代入式（1），可以得到位移{x}。

在频率空间中

其中ν为频率，j为单位复数，j2=-1，因此在得到{x}后很容易获取

1.2 载荷识别

在线性系统中，传递函数的定义是输出除以输入。如果输入是力，输出是加速度，第i个自由度的输入载荷Fi到第j个自由度的加速度响应ẍj的传递函数为

若Fi是单位载荷（即Fi=1），传递函数等于单位激励力下的响应。在获取了传递函数后，第i个自由度的输入载荷Fi在第j个自由度的加速度响应为

当系统中有多个输入时，第j个自由度的总响应是每个激励引起的响应之和

对于m个输入、n个自由度的响应，可写成

其中[H]是由m×n个Hij构成的矩阵。

相应地，若已知系统的多个自由度的响应和对应的传递函数，可反推算出输入载荷

2 振动模型修正流程

提出如图1所示的振动模型修正流程。首先利用HyperMesh软件按照试验条件建立研究对象的有限元模型，然后利用Virtual.Lab软件计算出激励点到响应点的传递函数，再利用实测的振动测试数据和仿真计算的传递函数及矩阵求逆方法进行载荷识别与振动响应计算。

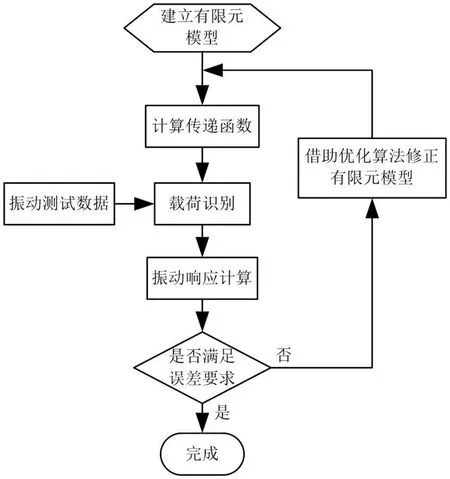
图1 振动模型修正的流程

若反推算出的振动响应与实测的振动响应有较大误差，需要借助优化算法修正有限元模型（如连接刚度、材料弹性模量等有限元模型的参数），修正后的有限元模型传递函数将发生变化，仿真计算的振动响应亦发生变化，需要与试验测试的振动响应继续对比。通过优化算法进行模型修正的迭代，最终可使仿真计算振动响应与试验测试振动响应小于预定误差。

3 计算实例

3.1 分析模型

某地铁车辆辅助变流器通过8个柜体吊耳与车体底架相连，内部主要动力部件为变压器、电抗器和风机，即为柜体振动的来源。在实验室条件下，为了模拟辅助变流器吊装在车体底架上的状态，将辅助变流器吊装在试验台架上。辅助变流器与试验台架中间隔着梯形金属垫块，通过较长的螺栓紧固相连。图2为布置在辅助变流器上的三向加速度传感器测点示意图，P1-P4为风机的4个安装孔附近的测点，P5-P8为变压器的4个安装孔附近的测点，P9-P16为柜体8个吊耳安装孔附近的测点，P17-P20为电抗器的4个安装孔附近的测点。

利用HyperMesh软件对辅助变流器柜体进行网格划分，可以得到如图2所示的有限元模型，其中X向为竖直方向，Y向指向柜体吊耳左右两侧，Z向为纵向。分析模型中，拟通过辅助变流器柜体吊耳安装孔附近测点P9-P16的实测振动加速度，来反推算引起辅助变流器柜体振动的变压器载荷、电抗器载荷和风机载荷，并修正有限元模型中的不确定性因素。在试验状态下，通过分析可知，系统中不确定性最大的因素是辅助变流器柜体吊耳与试验台架之间的连接刚度。

图2 测点示意图

图3 有限元模型

3.2 试验数据分析

测试辅助变流器柜体吊耳安装位置附近的振动加速度，测试工况分为满载、半载和空载3种工况。由于各测点的测试数据文件较多，限于篇幅限制，仅列出部分测点的测试数据。图4为P13在满载、半载和空载工况下，X向500 Hz以内的振动加速度频谱曲线。通过上述测试可以看出，在3个工况下，500 Hz以内X、Y和Z向的最大加速度峰值均在100 Hz处；半载和空载工况的振动规律基本相同，满载工况因风机转速大、气流大、变压器和电抗器负载大，在不同频率点的峰值增多，半载和空载下的振动可以认为是100 Hz处的单频振动问题；从振动幅值上看，100 Hz处X向和Y向的振动幅值数量级相同，高出Z向的振动幅值一个数量级。由于主要振动集中在变压器磁致伸缩效应引起的100 Hz处，因此振动模型修正主要针对100 Hz处的振动幅值。

3.3 传递函数计算与分析

建立有限元模型后，不需要定义实际的载荷激励，可以用Virtual.Lab软件计算与分析载荷输入点到柜体吊耳之间的传递函数。图5为变压器处P5的X、Y和Z向激励到柜体吊耳处P13的X、Y和Z向传递函数，可以看出：

图4 P13在不同工况下的振动加速度

(1)P5的X、Y和Z向激励到P13的X向传递函数曲线除在14 Hz、31 Hz、96 Hz、160 Hz和258 Hz处存在较大峰值外，在整个低频段整体幅值较低，而在频率大于350 Hz以后，曲线幅值变大；

(2)P5的X、Y和Z向激励到P13的Y向和Z向传递函数曲线幅值在低频段均较低，而在频率大于350 Hz以后，传递函数曲线幅值变大。

图5 P5到P13的传递函数曲线

3.4 载荷识别

在得到测点的振动响应测试数据和传递函数曲线后，可根据式（16）计算得到引起振动响应的载荷。图6为半载工况下变压器处P5－P8对辅助变流器柜体X向作用的载荷谱，对Y向和Z向作用的载荷谱未列出。可以看出，变压器对辅助变流器柜体作用的载荷最大值主要集中在100 Hz处，此外在24 Hz处也有小的载荷峰值。从数值上看，变压器对辅助变流器柜体X向作用的载荷较小，而对辅助变流器柜体Y向和Z向作用的载荷较大。对X向作用的载荷中，P5和P6处的载荷大，P7和P8处载荷小；对Y向作用的载荷中，P5和P6处的载荷大，P7和P8处载荷小；对Z向作用的载荷中，P5和P6处的载荷小，P7和P8处的载荷大。

半载工况下，变压器P5和P8处的Y向载荷的实部和虚部如图7所示，可以看出P5和P8处的Y向幅值基本相等、方向相反。

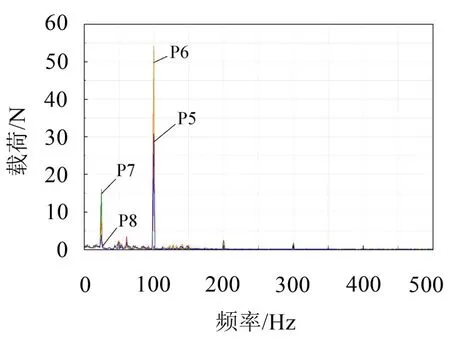
图6 变压器对辅助变流器柜体X向作用的载荷

3.5 修正方案建立

振动修正需要定义修正变量、修正目标和修正策略。修正变量是指可以调节的量，修正目标随修正变量的变化而变化，修正策略是指如何进行修正变量的调整，使得修正目标达到预期的值。因半载工况是辅助变流器实际使用中最普遍的一种工况，因此振动模型修正以半载工况计算为主。针对辅助变流器柜体与试验台架之间的连接，利用Virtual.Lab软件分别采用刚性和柔性两种连接方式进行仿真，发现辅助变流器柜体吊耳的仿真结果与试验结果在100 Hz处均有较大的误差，因此，可以选择辅助变流器柜体吊耳与试验台架的连接刚度作为修正变量。每个柜体吊耳与试验台架有3个平动刚度（KX、KY、KZ）和 3 个扭转刚度（KRX、KRY、KRZ）。辅助变流器柜体共有8个吊耳，故有48个修正变量，将其定义为：Kij（i=9,10,…,16；j=X,Y,Z,RX,RY,RZ）。修正变量的初始值定义如下：平动刚度为108N/m，扭转刚度为108N·m/rad。

根据辅助变流器柜体吊耳各测点的计算振动加速度Pij_sim和试验振动加速度Pij_test，定义各吊耳振动加速度相对误差的绝对值

由于修正变量较多，选择被广泛应用于优化相关领域、具有全局收敛性和超线性收敛速度的序列二次规划算法进行自动修正[8–9]，通过调整修正变量，使得修正目标达到期望值为min(Object)，将多输出模型修正问题转化为单输出模型修正问题。

3.6 修正前后振动响应对比

基于半载工况的振动数据修正前后各测点100 Hz处仿真与试验振动响应幅值的相对误差，如表1所示。

可以看出修正后半载工况下各测点相对误差均小于10%。同时，空载工况下的相对误差也小于10%，证明了振动修正方法的正确性。由于满载工况下的辅助变流器柜体受力比较复杂，如受到风机、气流和噪声等的影响，基于半载工况的振动数据修正后，满载工况的误差有所偏大。

半载工况下，P13的X向仿真加速度频谱与试验加速度频谱对比分别如图8所示。

图8 P13处的仿真与试验加速度对比

表1 基于半载工况修正后各工况的相对误差

可以看出500 Hz以内的仿真加速度响应曲线与试验加速度响应曲线的规律和走势基本相同，峰值对应的频率完全吻合。经振动修正后的载荷和有限元模型可用于后续振动噪声计算，也可进行传递路径分析和模态贡献量分析，为找到降低振动噪声的方法提供必要的输入。

4 结语

以某地铁车辆辅助变流器柜体为例，将载荷识别技术与优化算法用于其振动修正，得出如下结论：

（1）基于振动试验数据和仿真传递函数，利用该修正方法可获得合理的有限元模型和激励载荷；

（2）计算实例中半载工况下，修正后的仿真振动响应与实测振动响应频谱基本重合，主要峰值误差小于10%。空载工况也随之得到改善，由于满载工况下影响因素较多，仍存在一定误差，但总误差得到大幅缩减。

[1]张方，秦远田，邓吉宏.复杂分布动载荷识别技术研究[J].振动工程学报，2006，19(1)：81-85.

[2]朱凼凼，冯咬齐，向树红.基于频率响应函数的动力学模型修正方法研究[J].中国工程科学，2005，7(8)：89-94.

[3]芮强，王红岩，欧阳华江.机械结构动力学模型修正技术的现状与发展[J].装甲兵工程学院学报，2012，26(2)：1-8.

[4]徐张明，高天明，沈荣瀛，等.一种改进的利用频响函数进行有限元模型修正的方法[J].振动与冲击，2002，21(3)：43-45.

[5]毛玉明，郭杏林，赵岩，等.基于灵敏度分析的结构动态载荷识别研究[J].振动与冲击，2010，29(10)：1-3.

[6]许立富.航天器虚拟振动试验模型修正软件开发[D].哈尔滨：哈尔滨工业大学，2010.

[7]徐菁，张方，姜金辉.计算参数对数值修正载荷识别算法的影响[J].南京航空航天大学学报，2016，48(1)：143-148.

[8]宇振盛，张丽娜，秦毅.非线性优化问题的光滑化序列二次规划方法[J].上海理工大学学报，2015，37(4)：317-321.

[9]刘崇茹.基于序列二次规划算法的多馈入直流输电系统功率优化[J].电网技术，2007，31(19)：31-34+40.

Vibration Model Updating ofAuxiliary Converter Cabinets Based on Load Identification

DING Jie1,2,ZHANG Ping1,WANG Yong-sheng2,ZENG Ya-ping2,ZANG Xiao-bin2
(1.College of Civil Engineering and Mechanics,Xiangtan University,Xiangtan 412001,Hunan China;2.Technology Center,Zhuzhou CSR Electric Times Co.Ltd.,Zhuzhou 412001,Hunan China)

In order to improve the accuracy of the results of vibration response simulation for a metro vehicle’s auxiliary converter cabinet,a method of vibration model updating combining the load identification with optimization algorithm is proposed.Firstly,the transfer function between excitation and vibration response is calculated by means of the finite element model of the auxiliary converter cabinet,and the excitation spectrum applied at the measurement points of the auxiliary converter cabinet is calculated by using the transfer function and the test data.Then,sequence quadratic programming is adopted to carry out the model updating for the finite element model.The multi-output model updating problem can be transferred into a single-output model updating problem by constructing a proper objective function.Finally,the modified finite element model is analyzed and the vibration response results between numerical simulation and test are compared to verify the correctness of the proposed model updating method.The method can be used to create the necessary conditions for further vibration and noise reduction of the auxiliary converter cabinet.

vibration and wave;load identification;model updating;transfer function;matrix inverse;optimization algorithm

TH 113.1

：A

：10.3969/j.issn.1006-1355.2017.04.004

1006-1355(2017)04-0015-05+51

2016-12-09

丁杰（1979－），男，湖南省常德市人，博士生，主要研究方向为一般力学与力学基础、变流器结构仿真与热仿真研究。

Email:dj8083@126.com

张平（1955－），男，湖南省郴州市人，博士生导师，主要研究方向为固体力学与流变力学。

E-mail:zhangp@xtu.edu.cn