基于改进直线涡元诱导速度模型的旋翼自由尾迹计算方法∗
周来宏窦景欣 张居乾 闻邦椿
(东北大学机械工程与自动化学院,沈阳 110819)
基于改进直线涡元诱导速度模型的旋翼自由尾迹计算方法∗
周来宏†窦景欣 张居乾 闻邦椿
(东北大学机械工程与自动化学院,沈阳 110819)
通过设置涡核模型的角度条件,使涡核模型在极限状态下仍保持收敛,进而改进了利用Biot-Savart定律计算直线涡元对空间任意一点诱导速度的模型;桨叶气动模型采用Weissinger-L升力面理论模拟;自由尾迹的求解采用PIPC松弛迭代算法结合具有二阶精度的CB2D时间步进算法.利用上述模型和算法对某型号旋翼的尾迹进行数值计算,结果显示:利用改进涡核模型计算的桨尖涡径向位移收缩更加明显,这与实际情况更加接近;利用改进涡核模型得到的自由尾迹结果与实验数据吻合的更好.上述结论可以证明,新建立的旋翼自由尾迹模型提高了原有模型的准确性.
无人机, 旋翼, 桨尖涡, 直线涡元, 诱导速度, 自由尾迹
引言
旋翼式无人机如四旋翼无人机、倾转旋翼无人机、无人直升机等,已成为旋翼航空器领域的研究热点,而旋翼尾迹对这类航空器旋翼的流场、载荷、噪声及振动水平等,会产生十分重要的影响.尾迹卷起形成的强烈集中且自由畸变桨尖涡,会反作用于旋翼,改变桨叶迎角,使桨盘平面产生强烈的下洗流和复杂的诱导速度场,进而影响旋翼的气动特性.因此,研究旋翼尾迹,对提高旋翼式无人机的飞行品质和稳定性,以及给飞行控制提供置信度更高的计算模型,都有相当重要的意义.
目前,旋翼尾迹的研究方法主要有动态入流理论、自由尾迹方法和计算流体力学(CFD)方法.动态入流理论如Pitt-Peters动态入流模型[1,2]、Peters-He有限状态尾迹模型[3,4],虽然计入了旋翼的动态特性,但对尾迹畸变的处理过于简单,因此模型的准确性和通用性受到质疑;CFD方法[5,6]近些年取得了长足的进步,但其计算量大,计算资源要求高,目前还处于发展阶段;自由尾迹方法[7]是现阶段最适合用于分析旋翼尾迹的方法,它用Lagrange法描述流场,用涡元和控制节点离散尾涡,并允许尾涡以当地气流速度自由运动,这样可以自动捕捉尾迹畸变,进而得出更真实的桨盘诱导入流分布和空间任意一点的尾迹诱导速度,是一种速度较快,精度较高的分析方法.
用自由尾迹方法求解旋翼尾迹时,要计算直线涡元对控制节点的诱导速度,通常采用Biot-Savart定律计算,涡核模型采用 Scully[8]、Vatistas[9]等模型计算.但对于目标节点不在以直线涡元为轴的圆柱体内,且距离直线涡元相对较近的情况,用上述涡核模型计算出的诱导速度存在较大误差,进而影响旋翼尾迹的求解准确性.
为了解决上述问题,探索了一种改进的直线涡元诱导速度计算模型,即给涡核模型设置了角度条件.当目标节点与直线涡元夹角满足条件时,会以节点到涡元中点的距离取代节点到直线的垂直距离,这样使涡核模型在极限状态下仍保持收敛,使计算模型更加符合Biot-Savart定律的物理意义.论文最后用算例验证了该模型,与原有的涡核模型相比,基于改进直线涡元诱导速度模型,计算得到的旋翼自由尾迹更加接近实验数据.
1 计算方法
1.1 桨叶气动模型
采用Weissinger-L升力面理论模拟旋翼桨叶,它是一种简化升力面模型.如图1所示,桨叶沿展向分为若干段,每一小段中附着涡位于桨叶1/4弦线处,且附着涡环量为常数.每小段的控制点位于3/4弦线中点处.附着涡环量沿桨叶展向和弦向变化形成尾随涡系和脱体涡系.尾随涡强度为相邻两展向微段附着环量之差;脱体涡强度为相邻方位角上两微段附着环量之差.尾随涡和脱体涡组成旋翼尾迹的近尾迹.
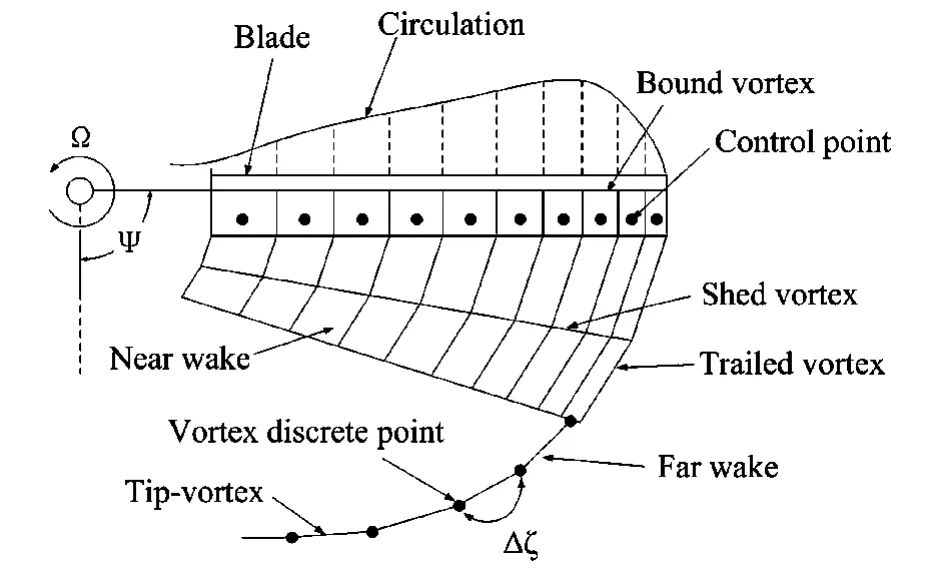
图1 桨叶附着涡系及尾迹模型Fig.1 Model of blade bound votex and wake
远尾迹主要由近尾迹涡片外侧快速卷起形成的桨尖涡组成.桨尖涡由单根涡丝表示,将其离散为有限段直涡丝,并由节点连接.单根涡丝的控制方程表达式为:

式中ψ和ζ分别为桨叶方位角和尾迹寿命角,Ω为旋翼转速,r(ψ,ζ)为桨尖涡空间位置向量,V∞为旋翼轴向来流速度,Vind为附着涡、近尾迹及远尾迹对空间点r(ψ,ζ)的诱导速度,由Biot-Savart定律确定.
1.2 涡核半径确定方法
在利用Biot-Savart定律计算诱导速度时,涡核半径rc是一个非常重要的参数,考虑涡的耗散效应,计算中常用两种方法:一种是涡核半径固定,涡强度按指数率衰减;另一种是涡强度固定,涡核半径随时间增长.考虑到涡粘性的影响,采用了Bhagwat等人对Lamb-Oseen涡模型进行修正后的涡核半径公式:

式中,r0为初始涡核半径,αL=1.25643为 Lamb-Oseen常数,ν为层流运动粘性系数,δ为涡粘性参数,δ可以写成涡雷诺数相关的表达式:

1.3 求解方法
用数值方法求解控制方程(1)时,需先对方程进行离散[10],采用五点中央差分法离散方程,如图2 所示,以(l+1/2,k+1/2)点的一阶差分项来近似控制方程中的偏微分项:


图2 五点中央差分法示意图Fig.2 Discretized computational domain for finite difference scheme
文章采用收敛性较好的PIPC算法,即伪隐性预估修正迭代算法求解尾迹的周期稳态解,并将其作为初值,采用具有2阶精度的显式时间步进算法CB2D算法,计算最终的旋翼尾迹结果.
2 改进的直线涡元诱导速度模型
在求解旋翼尾迹时,需利用Biot-Savart定律计算各段直线涡元对远尾迹节点的诱导速度.计算公式为:
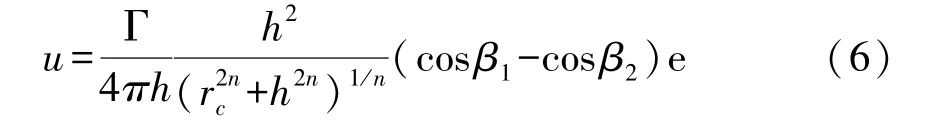
为证明简便,取n=1,即采用Scully涡核模型分析,其它涡核模型可以得到相似的结果.如图3所示,节点P到直线涡元AB的垂直距离h表示为:

其中rm为P到AB中点的距离,当b=1时,h=rm,考虑极限:


图3 直线涡元诱导速度示意图Fig.3 Induced velocity of straight vortex line segment
即当h≪rm时,涡核模型不收敛,在这种情况下仍采用式(6)计算诱导速度会产生很大的误差,为解决这一问题,对式(6)做如下修正:
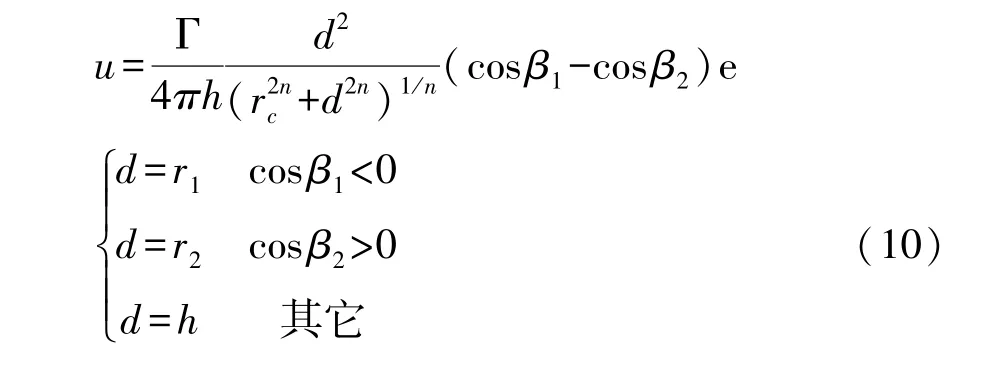
式中,r1、r2分别为P点到 A、B两点的距离.按式(10)取 b=1时的极限,结果与式(8)相同;当 b→0(取 β1、β2趋近于 0,β1、β2趋近于 π 时情况类似)时,取极限:

因此,b→0时涡核模型收敛,即采用式(10)计算得到的诱导速度,无论附着涡、近尾迹、远尾迹的直线涡元与目标节点的位置关系如何,都可以得到较高的计算精度.
3 算例分析
算例旋翼采用两片桨叶,选用NACA2415翼型,旋翼参数为:桨叶半径40.64cm;弦长4.25cm;桨尖马赫数0.26;拉力系数0.005;转速2010r/min,计算7圈自由尾迹.
图4为用两种涡核模型计算的桨尖涡沿z轴的诱导速度比较,由图可以看出,使用原始涡核模型计算的诱导速度振幅较大,这会使尾迹的计算结果也产生较大的波动.图5为采用两种涡核模型计算的桨尖涡径向位移随寿命角变化的比较,两种方法的结果可以近似看做一种振幅和峰值衰减的振动,这与相关的实验结果一致,但改进模型的衰减更加明显,即尾迹收缩更显著,这与实际情况更加接近.
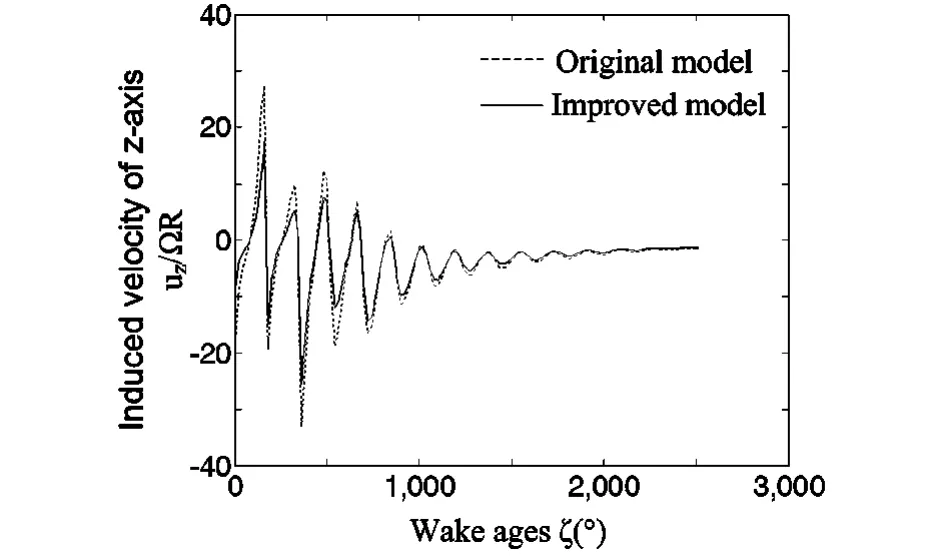
图4 桨尖涡z轴诱导速度比较Fig.4 Comparison of the rotor tip vortex induced velocity in z-axis

图5 桨尖涡径向位移比较Fig.5 Comparison of radial displacement of the rotor tip vortex
图6(a)、(b)两种涡核模型得到的尾迹分别与实验结果对比,其中(a)为原始模型,(b)为改进后模型,实验数据来自文献[11].结果显示,采用改进涡核模型的尾迹与实验值吻合得更好;原始涡核模型由于一味采用垂直距离h,使尾迹在x轴负半圈产生了一定的累积误差.

图6 悬停状态下自由尾迹计算与试验结果对比Fig.6 Comparison of computational and experimental results of hovering free wake
4 结论
将Weissinger-L升力面理论,Lamb-Oseen涡模型,PIPC和CB2D算法综合运用到旋翼悬停自由尾迹计算中,取得良好的效果.对Biot-Savart定律中的涡核模型做了改进,使尾迹节点诱导速度得到了修正,计算得到的桨尖涡径向位移收缩更加明显,与实际尾迹形状更加接近.利用两种涡核模型得到的自由尾迹分别与实验结果对比可以看出,用改进后的涡核模型计算的自由尾迹与实验结果吻合得更好,证明新建立的理论模型是有效的.
1 Dale M P,David A P.Theoretical prediction of dynamic inflow derivatives.Vertica, 1981,5(1):21~34
2 David A P,He C J.A closed-form unsteady aerodynamic theory for lifting rotors in hover and forward flight.In:AHS 43rd Annual Forum Proceeding, Louis Missouri,1987:840~854
3 David A P,Morillo J A.New developments in dynamic wake modeling for dynamic applications.Journal of the A-merican Helicopter Society, 2003,48(2):120~127
4 David A P,He C J.Finite state induced flow models partⅡ:Three dimensional rotor disk.Journal of Aircraft,1995,32(2):323~326
5 Conlisk A T.Modern helicopter roar aerodynamics.Progress in Aerospace Science, 2001,37:419~475
6 黄灿,赵永辉.基于CFD系统辨识的气弹分析及GPU并行算法初探.动力学与控制学报,2015,13(2):86~91(Huang C,Zhao Y H.Identification of CFD-based aeroealstic analysis and GPU parallel computing.Journal of Dynamics& Control, 2015,13(2):86~ 91 (in Chinese))
7 Landgrebe A J.An analytical method for predicting wake geometry.Journal of the American Helicopter Society,1969,14(4):20~32
8 Scully M.Computation of helicopter rotor wake geometry and its influence on rotor harmonic airloads[Ph.D Thesis].Cambridge:Massachusetts Institute of Technology,ASRL TR,1975:178-1
9 Vatistas G H,Kozel V,Mih W C.A simpler model for concentrated vortices.Experiments in Fluids, 1991, 11(1):73~76
10 李春华,徐国华.悬停和前飞状态倾转旋翼机的旋翼自由尾迹计算方法.空气动力学学报,2005,23(2):152~156(Li C H,Xu G H.The rotor free-wake analytical method for tiltrotor aircraft in hover and forward flight.Acta Aerodynamica Sinica, 2005,23(2):152~156 (in Chinese))
11 Bhagwat M J.Mathematical modelling of the transient dynamics of helicopter rotor wakes using a time-accurate free-vortex methods[Ph.D Thesis].Maryland:College Park, University of Maryland, 2001
CALCULATION METHOD OF ROTOR FREE WAKE BASED ON AN IMPROVED INDUCED VELOCITY MODEL OF STRAIGHT VORTEX LINE SEGMENT∗
Zhou Laihong†Dou Jingxin Zhang Juqian Wen Bangchun
(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)
The vortex core model can keep the convergence in the limit state by setting the model angle conditions so as to improve the model of straight vortex line segment induced velocity calculated by the Biot-Savart law at every point.The model of the blade is simulated by Weissinger-L lifting-surface theory,while PIPC algorithm and CB2D algorithm are used to solve the rotor free-wake.The models and algorithms above are then combined to numerically calculate the wake of certain rotor.The results show that the radial displacement of tip vortex calculated by the improved vortex core model contracts remarkably.This is closer to the actual situation than previous model.In addition,the result of free-wake calculated by the improved vortex core model agrees with the experimental data perfectly.Therefore,the improved free-wake model of rotor is more accurate than the original one.
UAV, rotor, tip vortex, straight vortex line segment, induced velocity, free-wake
18 March 2016,revised 5 December 2016.
10.6052/1672-6553-2017-062
2016-03-18收到第1稿,2016-12-05收到修改稿.
∗国家自然科学基金(51375080)、中央高校基本科研业务费专项资金(N150306002)
†通讯作者 E-mail:lai_h@126.com
∗The project supported by the National Natural Science Foundation of China(51375080) and the Fundamental Research Funds for the Central Universities(N150306002)
†Corresponding author E-mail:lai_h@126.com

