氧化锌纳米线振动问题研究
刘赛赛 王立峰
(南京航空航天大学机械结构力学及控制国家重点实验室,南京 210016)
氧化锌纳米线振动问题研究
刘赛赛 王立峰†
(南京航空航天大学机械结构力学及控制国家重点实验室,南京 210016)
采用连续介质理论与分子动力学模拟相结合的方法,研究了氧化锌纳米线的振动问题.建立了氧化锌纳米线核壳模型,解释其等效杨氏模量及压电常数的尺寸效应.通过连续介质理论求得氧化锌纳米线振动固有频率,并与分子动力学模拟得到的结果进行对比.研究表明,氧化锌纳米线在极化方向的等效拉伸杨氏模量随着横截面尺寸的增加而逐渐增大,且通过核壳模型分别求得核、壳拉伸杨氏模量.拟合得到的等效拉伸杨氏模量与分子动力学方法获得的等效拉伸杨氏模量符合得很好.根据连续介质理论得到等效弯曲杨氏模量,发现等效弯曲杨氏模量也随着横截面尺寸的增加而增大.氧化锌纳米线极化方向的压电耦合能力比一般压电陶瓷好,压电常数随着横截面尺寸的增加逐渐减小.氧化锌纳米线在不同温度条件下的振动频率没有明显变化,在不同外电场条件下的振动频率有显著变化.分子动力学模拟得到不同横截面尺寸的氧化锌纳米线振动频率不同.根据连续介质理论,求得悬臂Timoshenko梁模型相应尺寸的振动频率,发现横截面的尺寸越大,连续介质理论与分子动力学模拟得到的振动频率越接近.
氧化锌纳米线, 分子动力学, 尺寸效应, 压电效应, 振动
引言
氧化锌纳米线在光学、力学等方面具有独特的压电性、光电性,而使其备受关注.研究发现氧化锌是一种宽带隙半导体,在室温下仍有很强的导电性,因此科学界认为氧化锌有望取代氮化镓成为半导体发光二极管和半导体激光二极管的新材料[1].
国内外对于纳米氧化锌的力学、电学性能等做了大量研究.王中林等利用氧化锌纳米线发明了纳米发电机[2,3].Corso 等采用量子力学从头计算方法,发现在四面共价半导体中,氧化锌纳米线的压电性能最好[4].Hill等通过局域密度近似的平面波伪势密度泛函理论,发现可以通过改变氧化锌的晶格常数实现其压电性质的变化[5].基于Berry相理论[6-8],Noel等得到氧化锌的压电常数和 Wannier函数理论结果符合很好[9],Catti等测量了纤锌矿、闪锌矿及硫化锌的压电张量[10].Lucas等通过纳米压痕技术,利用原子力显微镜测量了氧化锌纳米带的杨氏模量[11],Asthana等实验研究了氧化锌纳米线机械性能的尺寸效应[12],Xu等用扫描电子显微镜测量了氧化锌纳米线在不同载荷作用下的机械性能[13],Agrawal等利用实验和计算相结合的方法得到氧化锌纳米线的体杨氏模量约为140GPa[14].然而由于生产技术、纳米氧化锌各项异性、实验设备精确度、纳米氧化锌材料的选取等原因,对于纳米氧化锌杨氏模量的实验测量结果很不一致[15].Ewald[16-18]求和方法的提出,使通过计算机模拟来研究氧化锌纳米线、纳米管等的机械性质得到迅速发展[19-21].Zaoui等研究了压强对氧化锌剪切模量的影响[22],Wang等分析了温度对氧化锌纳米线机械行为的影响[23],Sun等研究了闪锌矿压强、温度与体积之间的关系[24].
压电梁振动问题一直是备受关注的问题,曹树谦和郭抗抗研究了压电发电悬臂梁非线性动力学响应问题,给出了不同结构参数及外激励参数下系统响应特性的数值结果和实验结果[25].彭剑等研究了时滞反馈作用下压电梁的参数共振问题,分析了轴力等因素对稳定性区域的影响[26].随着微机电系统(MEMS)技术的发展[27,28],为了在单位体积内实现更多的功能,人们开始研制纳机电系统(NEMS).纳机电系统的研究有望促进医疗技术、信息传播、军事国防、生产制造等的发展.Liu和Wang通过半量子化分子动力学方法研究了单壁碳纳米管振动问题,发现在低温、高频振动情况中,碳纳米管具有明显的量子效应[29].Ke等基于非线性理论研究了压电纳米梁热电力耦合振动(thermoelectricmechanical vibration)[30].纳米压电梁结构是最简单的纳机电系统,压电梁振动研究是基于振动的机械传感器研制的基础,对压电悬臂梁振动的研究,有利于提高以新型压电材料为基础的能量采集器的效率.本文主要研究悬臂氧化锌纳米线振动问题,关注温度、外电场强度对振动频率的影响.
1 氧化锌纳米线力学性质的分子动力学模拟
1.1 模型建立
本文研究纤锌矿结构氧化锌纳米线,初始结构如图1(a),红色为氧原子、灰色为锌原子,图1(b)为氧化锌纳米线模型,两端黄色为固定层,横截面如图1(c),计算所用到的氧化锌纳米线尺寸、序号见表1.b、h、L分别为模型的宽、高和长,单位为纳米,Δb、Δh 是壳不同边的厚度[19,31,32],取 Δb=0.406 nm,Δh=0.469nm,z轴垂直于延长方向.
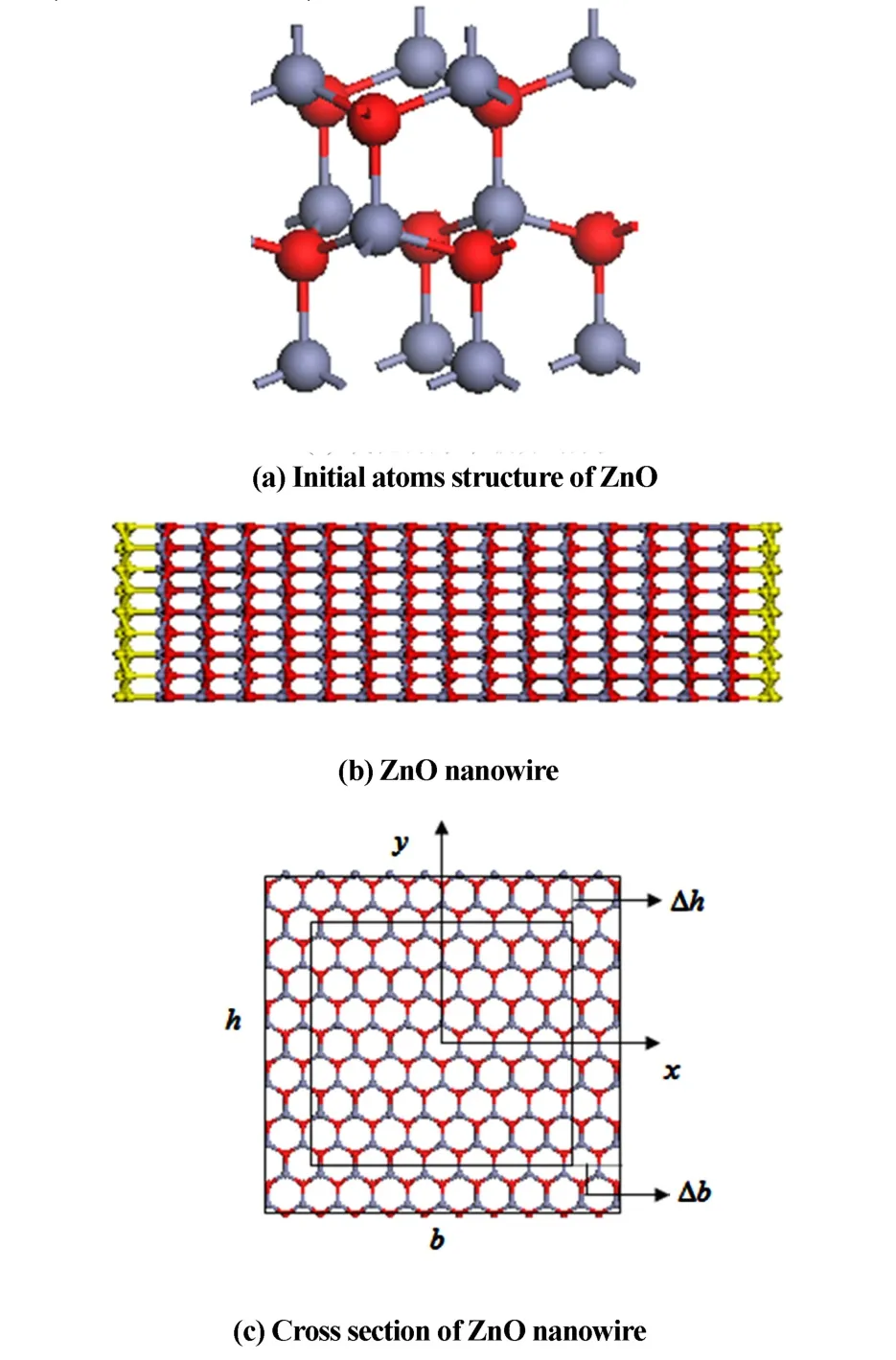
图1 氧化锌结构图Fig.1 Structures of ZnO
氧化锌纳米线原子间的相互作用采用Buckingham 对势[33,34]:

式中rij是离子i和离子j之间距离,qi是离子i所带电荷,A、ρ、C是该势的参数,取值见表 2.等式右边第一项是长程库伦作用,第二项是短程相互排斥作用,第三项是短程相互吸引作用.氧离子之间既有库伦作用又有短程作用,锌离子之间只有库伦作用,氧离子和锌离子之间忽略短程相互吸引作用,只有库伦作用和短程相互排斥作用,计算长程库伦作用采用 Wolf算法[35,36],对库伦作用中 r-1项进行截断,提高计算效率.本文阻尼系数取0.4,截断半径取1nm,可实现Wolf求和的最佳收敛[35].在分子动力学中Wolf算法要求采用周期性边界条件,我们将氧化锌纳米线模型放入较大的真空模拟盒中,避免不同模拟盒中的氧化锌纳米线之间存在相互作用,近似模拟单根纳米线的情况.

表1 氧化锌模型大小及序号Table 1 Size and serial numbers of ZnO nanowires
1.2 等效拉伸杨氏模量
压电材料单位体积总势能[37]:

式中Uv是单位体积总势能,是外电场恒定时的弹性系数,εij是应变张量,是应变恒定时的介电常数,Ei是外电场矢量.当外电场为零时,z方向的杨氏模量简化为:

式中U是总势能,V是氧化锌纳米线的体积.
将模型完全弛豫后固定两端,固定层向两侧各拉伸 ΔL=0.002nm,应变 ε=2ΔL/L,再次弛豫后得到总势能U,如此重复50次,得到总势能与应变关系曲线图和应力与应变关系图.图2为表1中No.2纳米线的总势能、应力与应变关系图.根据总势能和应变关系,由式(3)可得到拉伸杨氏模量.

图2 No.2氧化锌纳米线Fig.2 ZnO nanowire (No.2)
在轴向拉伸载荷作用下,氧化锌纳米线杨氏模量可看作是由核、壳的杨氏模量共同作用的结果如图1(c).设核的杨氏模量为Yc,壳的杨氏模量为Yc+Y1,则拉伸等效杨氏模量为[38]:

式中Ys为等效拉伸杨氏模量,A为模型横截面面积,A1为壳的横截面面积,A2为核的横截面面积.
用截面内的原子个数比代替截面面积比,对表1中的氧化锌纳米线进行分子动力学模拟,得到的拉伸杨氏模量与截面内的原子个数比通过最小二乘法拟合,如图3.得到核、壳杨氏模量分别为Yc=184.02GPa,Yc+Y1=81.10GPa,进一步得到连续介质等效杨氏模量Ys.从图4可以看出,连续介质等效杨氏模量Ys与分子动力学模拟得到的杨氏模量Y符合得较好.

图3 拉伸杨氏模量与原子数比拟合曲线Fig.3 Fitting curve of tension Young′s modulus with the ratio of atoms shell and bulk

图4 拉伸杨氏模量与截面宽度的关系Fig.4 Relationship of Young′s modulus and width for ZnO nanowires
1.3 等效弯曲杨氏模量
为使模型简化,假设梁在受载荷作用时,垂直于轴线的平面在弯曲过程中始终垂直于轴线,即梁受纯弯曲载荷作用.
当梁受到纯弯曲载荷作用时,截面上的弯矩为

式中ρ′为梁的曲率半径,I1、I2分别是壳、核截面惯性矩.
由弯矩平衡方程得:

式中Yb为等效弯曲杨氏模量,I为模型整体的截面惯性矩.
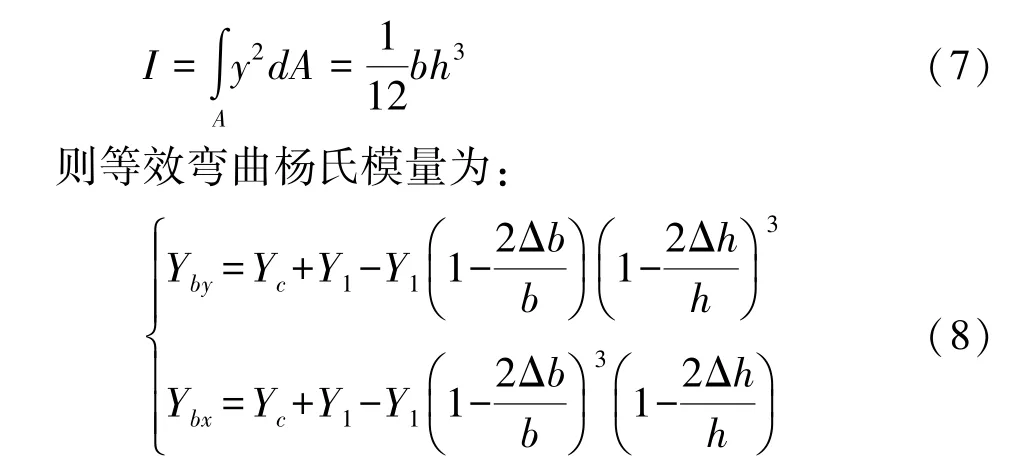
根据 Yc= 184.02GPa,Yc+Y1= 81.10GPa,得到等效弯曲杨氏模量与截面y方向尺寸关系如图5所示,Yby、Ybx分别是氧化锌纳米线沿y、x方向的弯曲杨氏模量.

图5 等效弯曲杨氏模量与截面高度的关系Fig.5 Relationship of equivalent bending Young′s modulus and height for ZnO nanowires
从图5可以看出,氧化锌纳米线的等效弯曲杨氏模量都随着截面尺寸的增加而增大.然而,由于氧化锌的各项异性,如表1近似正方形横截面的氧化锌纳米线,在上述两个方向的等效弯曲杨氏模量不完全相同.
1.4 压电常数的计算
极化强度由电子-原子核和锌氧离子相对位移变化共同作用的结果[34],当忽略前者时,氧化锌极化方向的平均极化强度由下式决定:

本文仅研究氧化锌纳米线极化方向压电性质,有:

由式(9)和式(10)得:

式中D是电位移,d是压电常数,σ是应力.根据上式得到表1中压电常数与其横截面x方向尺寸关系如图6所示.从图6中可以看出随着氧化锌纳米线尺寸的增加,极化方向的压电常数逐渐减小,并趋于某一定值.对于序号10对应的横截面最大的氧化锌纳米线,其压电常数为 1.65×10-11C/N,与Momeni等的模拟结果符合较好[32].

图6 压电常数与截面宽度的关系Fig.6 Relationship of piezoelectric constant and section width
2 固有振动
2.1 分子动力学模拟
本文分子动力学模拟过程中采用正则系综(NVT),用 Nose-Hoover控温方法[39,40]使系统的温度保持在一定范围内.
对序号2氧化锌纳米线分别进行300K、500K、1000K控温模拟.从图7幅频曲线可以看出,温度变化对氧化锌纳米线的振动频率几乎没有影响.
对序号2模型,沿着z轴方向加外电场E,强度从-1.0V/nm 到 1.0V/nm,控制温度为 300K.如图8,横坐标为电场强度,纵坐标为前四阶振动频率.可以看出,对于本文研究的氧化锌纳米线,当电场强度大于-0.20V/nm时,其振动频率随着电场强度的增大而增大;当电场强度小于-0.37V/nm,其振动频率随着电场强度的减小而增大;当电场强度在约-0.37V/nm到-0.20V/nm时,氧化锌纳米线运动幅度过大,无法确定振动频率.
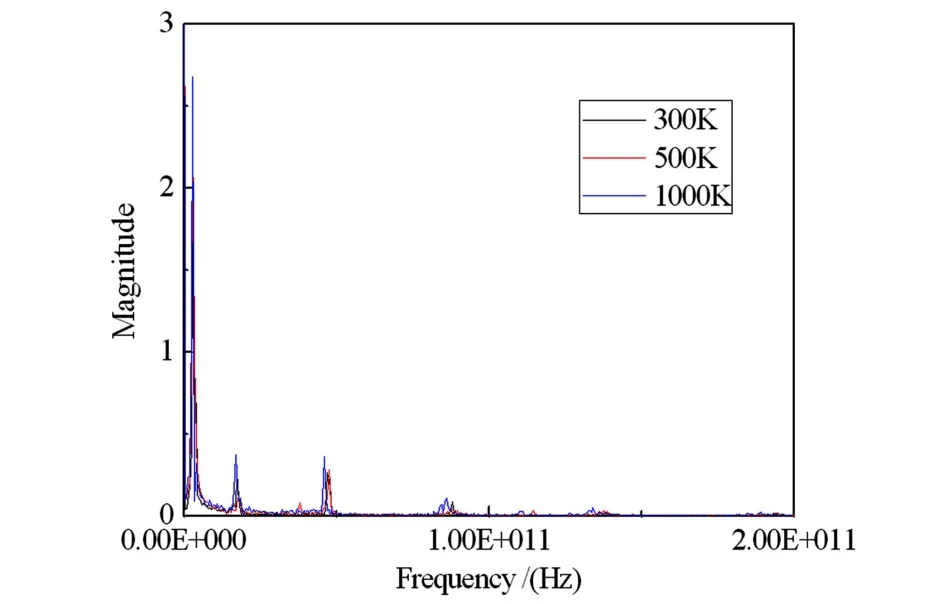
图7 温度对振动频率的影响Fig.7 Effect of temperature on the frequencies

图8 外电场强度对振动频率的影响Fig.8 Effect of electric field intensity on the frequencies
2.2 悬臂Timoshenko梁模型
为了预测氧化锌纳米线振动行为,建立悬臂Timoshenko梁模型[41],方向为沿轴向 x方向:

式中:E为杨氏模量,I为截面惯性矩,φ为弯曲转角,y为挠度,k为截面因子,A为横截面面积,G为剪切弹性模量,ρ为密度,t为时间变量,F=k1nqE为轴向力,n为单层锌(或氧)原子数,k1为比例系数,q为原子带电量,E为外电场强度.
采用悬臂梁边界条件[29]:


取截面因子 k=5/6,密度 ρ=5606kg/m3,泊松比υ=0.3.将上文得到的等效弯曲杨氏模量Yby代入行列式,得到不同厚度的氧化锌纳米线沿y方向振动的前四阶振动频率和分子动力学结果(MD)对比如图9.把等效轴力代入行列式,得到连续介质理论预测的振动频率,图10为氧化锌纳米线的振动频率随电场强度的变化.从图9可以看出,氧化锌纳米线的横截面尺寸越大,其连续介质力学结果和分子动力学模拟结果符合越好.从图10可以看出,氧化锌纳米线连续介质力学模型得到的振动频率和其分子动力学模拟得到的振动频率符合得很好.
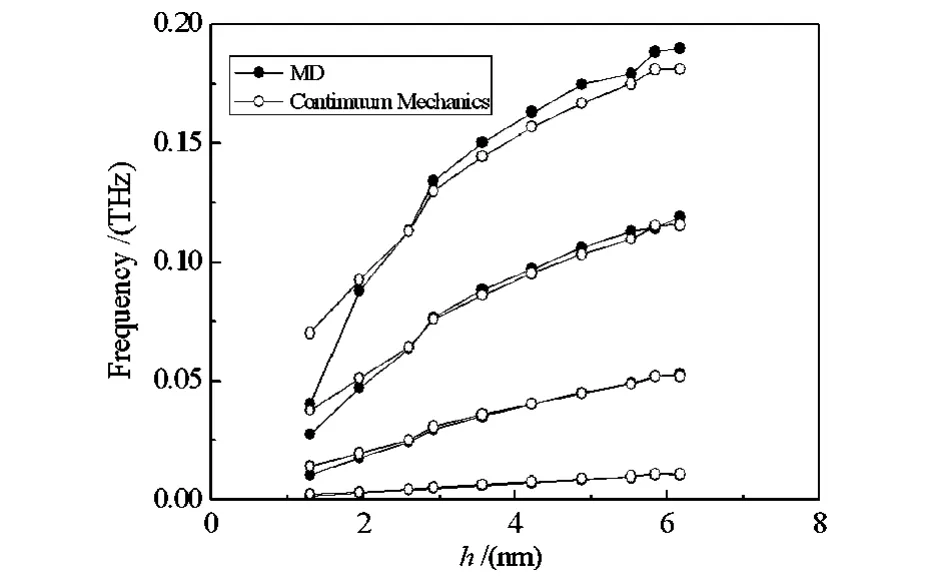
图9 氧化锌纳米线振动频率Fig.9 Frequencies of ZnO nanowires

图10 轴力作用下氧化锌纳米线振动频率Fig.10 Frequencies of ZnO nanowires under the axial force
3 结论
本文通过分子动力学模拟和连续介质理论相结合的方法,研究了氧化锌纳米线振动问题,得到如下结论:
(1)温度变化对悬臂氧化锌纳米线的振动特性没有明显影响,氧化锌纳米线在极化方向的拉伸杨氏模量、垂直极化方向的弯曲杨氏模量随着横截面尺寸的增加逐渐增大.
(2)氧化锌纳米线极化方向的压电常数随着横截面尺寸的增加逐渐减小,并趋向一定值;当极化方向电场强度大于-0.20V/nm(或小于-0.37V/nm)时,增加(或反向增加)极化方向外电场强度可以显著提高氧化锌纳米线的振动频率.
(3)悬臂Timoshenko梁理论求得的振动频率和分子动力学模拟得到的振动频率,在模型横截面尺寸较小时差别明显,在尺寸较大时符合得较好.
1 Ley L,Pollak R A,McFeely F R,et al.Total valenceband densities of states of III-V and II-VI compounds from x-ray photoemission spectroscopy.Physical Review B Condensed Matter, 1974,9(2):600~621
2 Wang Z L,Song J H.Piezoelectricnanogenerators based on zinc oxide nanowire arrays.Science, 2006,312:242
3 Song J H,Zhou J, Wang Z L.Piezoelectric andsemiconducting coupled power generating process of a single ZnO belt/wire.A technology for harvesting electricity from the environment.Nano Letter, 2006, 6:1656
4 Corso A D,Posernak M,Resta R,et al.Ab initio study of piezoelectricity and spontaneous polarization in ZnO.Physical Review B, 1994,50(15):10715~10721
5 Hill N A,Waghmare U.First-principles study of strain-electronic interplay in ZnO:Stress and temperature dependence of the piezoelectric constants.Physical Review B, 2000,62:8002
6 King-Smith R D,Vanderbilt D.Theory of polarization of crystalline solids.Physical Review B Condensed Matter,1993,47(3):1651
7 Vanderbilt D,King-Smith R D.Electric polarization as a bulk quantity and its relation to surface charge.Physical Review B Condensed Matter, 1993,48(7):4442
8 Resta R.Macroscopic polarization in crystalline dielectrics:the geometric phase approach.Reviews of Modern Physics, 1994,66:899
9 Novel Y,Zicovich-Wilson C M,Civalleri B,et al.Polarization properties of ZnO and BeO:An ab initio study through the berry phase and wannier functions approaches.Physical Review B, 2001,65(65):014111
10 Catti M,Noel Y,Dovesi R.Full piezoelectric tensors of wurtzite and zinc blende ZnO and ZnS by first-principles calculations.Journal of Physics and Chemistry of Solids,2003,64(11):2183~2190
11 Lucas M,Mai W J,Yang R,et al.Aspect ratio dependence of the elastic properties of ZnO nanobelts.Nano Letters, 2007,7(5):1314
12 Asthana A,Momeni K,Prasad A,et al In situ observa-tion of size-scale effects on the mechanical properties of ZnO nanowires.Nanotechnology, 2011,22(26):265712
13 Xu F,Qin Q Q,Mishra A,et al.Mechanicalproperties of ZnO nanowires under different loading modes.Nano Research, 2010,3(4):271
14 Agrawal R,Peng B,Gdoutos E E,et al.Elasticity size effects in ZnO nanowires——A combined experimentalcomputational approach.Nano Letters, 2008,8(11):3668
15 Dai L,Cheong C D,Sow C H,et al.Molecular dynamics simulation of ZnO nanowires:size effects, defects, and super ductility.Langmuir, 2010,26(2):1165
16 Darden T,York D,Pedersen L.Particle mesh Ewald:An N∗log(N) method for Ewald sums in large systems.Journal of Chemical Physics, 1993,98(12):10089
17 Bródka A, Sliwiński P.Three-dimensional Ewald method with correction term for a system periodic in one direction.Journal of Chemical Physics, 2004,120(12):5518~5523
18 Raymand D,van Duin A C T,Baudin M,et al.A reactive force field (ReaxFF) for zinc oxide.Surface Science,2008,602(5):1020
19 Kulkarni A J,Zhou M,Ke F J.Orientation and size dependence of the elastic properties of zinc oxide nanobelts.Nanotechnology, 2005,16(12):2749
20 Hu J,Liu X W,Pan B C.A study of the size-dependent elastic properties of ZnO nanowires and nanotubes.Nanotechnology, 2008,19(28):285710
21 Momeni K.EnhancedmechanicalpropertiesofZnO nanowire-reinforced nanocomposites:A size-scale effect.Acta Mechanica, 2014,225(9):2549
22 Zaoui A,Sekkal W.Pressure-induced softening of shear modes in wurtzite ZnO:A theoretical study.Physical Review B, 2002,66(17):553~562
23 Wang J, Kulkarni A J, Ke F J, et al.Novel mechanical behavior of ZnO nanorods.Computer Methods in Applied Mechanics and Engineering, 2008, 197(41):3182
24 Sun X W,Chua Y D,Song T,et al.Application of a shell model in molecular dynamics simulation to ZnO with zinc-blende cubic structure.Solid State Communications,2007,142(1):15
25 曹树谦,郭抗抗.压电发电悬臂梁的非线性动力学建模及响应分析.动力学与控制学报,2014,12(1):018(Cao S Q, Guo K K.Nonlinear modeling and analysis of piezoelectric cantilever energy harvester.Journal of Dynamics and Control, 2014,12(1):018 (in Chinese))
26 彭剑,李禄欣,马建军.时滞反馈作用下压电梁的参数共振分析.动力学与控制学报,2016,14(5):412(Peng J, Li L X, Ma J J.Parametric resonanceof piezoelectric beam with time-delayed feedback.Journal of Dynamics and Control, 2016,14(5):412 (in Chinese))
27 Ekinci K L, Roukes M L, Nanoelectromechanical systems.Review of Scientific Instruments, 2005,76(6):061101
28 Craighead H G.Nanoelectromechanical systems.Science,2000,290:1532
29 Liu R M,Wang L F.Thermal vibration of a single-walled carbon nanotube predicted by semiquantum molecular dynamics.Physical Chemistry Chemical Physics, 2015,17:5194
30 Ke L L,Wang Y S.Thermoelectric-mechanical vibration of piezoelectric namobeams based on the nonlocal theory.Smart Materials and Structures, 2012,21(2):025018
31 Chen C Q,Shi Y,Zhang Y S,et al.Size dependence of Young′s modulus in ZnO nanowires.Physical Review Letters, 2006,96:075505
32 Momeni K,Odegard G M,Yassar R S.Finite size effect on the piezoelectric properties of ZnO nanobelts:A molecular dynamics approach.Acta Materialia, 2012,60(13-14):5117-5124
33 Binks D J.Computational modelling of zinc oxide and related oxide ceramics.The Department of Chemistry of the University of Surrey,1994
34 Dai S X,Dunn M L,Park H S.Piezoelectric constants for ZnO calculated using classical polarizable core-shell potentials.Nanotechnology, 2010,21(44):445707
35 Wolf D,Keblinski P,Phillpot S R,et al.Exact method for the simulation of Coulombic systems by spherically truncated,pairwise r-1summation.Journal of Chemical Physics, 1999,110(17):8254
36 Gdoutos E E,Agrawal R,Espinosa H D.Comparison of the Ewald and Wolf methods for modeling electrostatic interactions in nanowires.International Journal for Numerical Methods in Engineering, 2010,84(13):1541
37 ANSI/IEEE Standard 176-1987
38 Wang L F, Hu H Y.Size effectson the effective Young′s modulus of nano crystal copper wires.International Journal of Computational Method, 2005,2(3):315~326
39 Nose S.A molecular dynamics method for simulations in the canonical ensemble.Molecular Physics, 1984,52:255
40 Hoover W.Canonical dynamics:Equilibrium phase-space distributions.Physical Review A, 1985,31:1695
41 Huang T C.The effect of rotatory inertia and of shear deformation on the frequency and normal mode equations of uniform beams with simple end conditions.Journal of Applied Mechanics, 1961,28(4):579~584
VIBRATION OF ZINC OXIDE NANOWIRES
Liu Saisai Wang Lifeng†
(State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
The vibration of Zinc Oxide(ZnO) nanowires is studied via molecular dynamics(MD) simulation and continuum theory.The size effect of equivalent Young′s modulus and piezoelectric constant for the ZnO nanowires are described by core-shell model.The equivalent tensile Young′s modulus of ZnO nanowires in polarization direction increases gradually with the increase of the cross section size.The equivalent tensile Young′s modulus predicted by continuum theory is in a good agreement with the MD result.The equivalent bending Young′s modulus also increases with the increasing cross section size.Meanwhile, the piezoelectric constants of ZnO nanowires are larger than that of piezoelectric ceramics.The piezoelectric constants of ZnO nanowires decrease with the rising of the cross section size.In addition,the vibration of the cantilevered nanobeam made of ZnO is simulated by MD.The vibration frequencies of a ZnO nanowire keep constant at different temperatures.When the cross section size becomes larger,the vibration frequencies predicted by continuum theory get closer to those obtained by MD well.
ZnO nanowires, molecular dynamics, scale effect, piezoelectric effect, vibration
1 October 2016,revised 22 November 2016.
10.6052/1672-6553-2017-063
2016-10-01收到第1稿,2016-11-22收到修改稿.
†通讯作者 E-mail:walfe@nuaa.edu.cn
† Corresponding author E-mail:walfe@nuaa.edu.cn

