新超混沌系统的动力学行为及自适应控制与同步∗
王贺元尹 霞
(辽宁工业大学理学院,锦州 121001)
新超混沌系统的动力学行为及自适应控制与同步∗
王贺元†尹 霞
(辽宁工业大学理学院,锦州 121001)
分析了一个新混沌系统的超混沌动力学行为,给出了这个未知参数的超混沌系统的自适应控制和同步问题的数值模拟结果.运用相图、分岔图、Lyapunov指数谱和庞加莱截面图,返回映射和功率谱等揭示了系统混沌行为的普适特征,基于Lyapunov稳定性理论,采用自适应控制方法将系统的混沌运动控制到一个不稳定的平衡点.此外,设计自适应控制律以实现超混沌系统的状态同步,仿真结果表明所提出的方法的有效性.
超混沌系统, 混沌控制, 同步, Lyapunov稳定性
引言
混沌系统是复杂的、类似于噪声的难以预测的非线性确定性系统,对初始条件及其参数变化的高度敏感性是它的一个显著特征,混沌广泛存在于物理、化学、生物学、地质学,以及社会科学等各个学科领域[1].然而,除了特殊应用需要混沌的效果外,在众多工程技术领域中需要改变混沌,因此,稳定混沌系统到周期轨道或平衡点的控制问题被普遍接受.
混沌同步是使两个混沌系统以同步的方式振动,两个混沌系统的动力学行为当初始条件接近时最终达到相同,第二个系统被第一个系统驱动.许多结果已经展示了如何在一定条件下实现混沌同步[2,3].同步混沌系统也有效地保证了创建安全的通信系统[4-6].混沌系统的控制与同步在物理系统、激光、等离子、电路、化学反应器、生态系统、生物系统都有潜在应用,例如心肺相互作用、对帕金森病人的大脑活动、太阳活动以及安全通信等方面均显示出混沌控制与同步的应用潜力.由于这些潜在的应用价值,在过去的几十年中科学家们一直致力于混沌控制与同步方面的研究,因此,混沌控制与同步的各种有效方法被陆续提出[1-11].超混沌系统大多是非严格反馈并不像只有一个正的Lyapunov指数的混沌系统,超混沌系统具有多个正的Lyapunov指数,这意味着,超混沌系统动力学在多个方向扩展,从而形成比混沌系统更复杂的行为和丰富的动态.因此,超混沌系统的控制与同步被认为比混沌系统的控制与同步有更广泛的应用.基于此,研究人员一直致力于实现超混沌控制与同步的目标[12-27].超混沌的控制与同步提出了更多的挑战,因为他们比混沌系统有更高的维度,表现出更复杂的动态,混沌控制与同步中的有些方法已扩展到超混沌的控制与同步领域,包括线性和非线性反馈控制与同步[13,14,18,19,24,25],自适应控制与同步[16,27], backstepping 技术[12,17],滞后控制与同步[20,21],主动控制[22],脉冲同步[23],滑模同步[26],及皮科拉-卡罗尔法[27].尽管固有的自适应控制技术,如前面所讨论的众多优点,在超混沌的控制与同步中的应用还没有得到充分的研究,大多数混沌控制方法仍无法实现超混沌系统的稳定和混沌跟踪[17].
本文中我们主要研究了一个不同于超混沌刘系统[28]的新超混沌系统的动力学行为和数值模拟以及控制与同步问题,我们工作的动机是探讨这个新超混沌系统和超混沌刘系统的异同.这个新超混沌系统的动力学行为和数值模拟以及控制和同步问题还没有系统的研究过,根据李雅普诺夫稳定性理论和自适应控制理论稳定超混沌系统到不稳定平衡点,实现两个超混沌系统之间的同步.论文安排如下.在第二部分,我们描述了此超混沌系统的动力学行为,给出了数值模拟结果.第三节我们研究新超混沌系统的稳定性,第四节我们讨论超混沌系统的同步,第五节我们提供数值模拟结果,最后一节是结论.
1 新超混沌的动力学行为及其数值模拟
考虑如下超混沌刘系统[28]
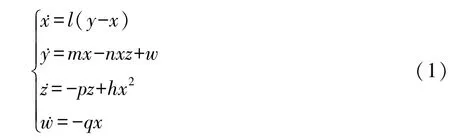
其中 l,m,n,p,q和 h 为常数参数.文献[28]给出了超混沌刘系统,讨论了当 l=10,m=40,n=1,p=2.5,h=4,q=10.6 时系统的动力学行为.本文研究了当l=8,m=25,n=2,p=4,h=5时超混沌刘系统的动力学行为和数值模拟以及自适应控制与同步问题.对于 l=8,m=25,n=2,p=4,h=5, 当 q=18时系统(1)有超混沌行为, 在平衡点 E0(0,0,0,0), 系统(1)被线性化,对应的Jacobian矩阵为:
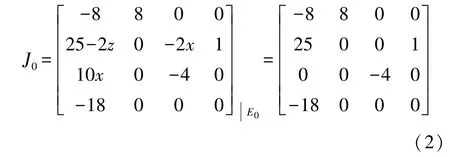

从(3)中我们看出有两个正的Lyapunov指数,因此, 系统(1)是超混沌系统, 并且 E0(0,0,0,0)是不稳定平衡点.这一段,我们研究当l=8,m=25,n=2,p=4,h=5时超混沌系统(1)的基本性质.
1.1 耗散性
1.2 混沌行为和数值模拟
当 l=8,m=25,n=2,p=4,h=5 时,系统(1)蕴含着丰富复杂的混沌动力学行为,图1~8展示了系统(1)的各种吸引子.图9是q变化时状态变量x的分岔图,图10是对应的最大Lyapunov指数.图11,12显示了不同q值下系统(1)庞加莱映射,图13是返回映射,图14是功率谱,他们均表明了系统(1)混沌特征.从分岔图9我们发现混沌区内有变化很宽的拟周期轨道窗口,吸引环面、拟周期轨道和极限周期在不同的q值交替出现,图5,6,8给出了几个准周期状态.
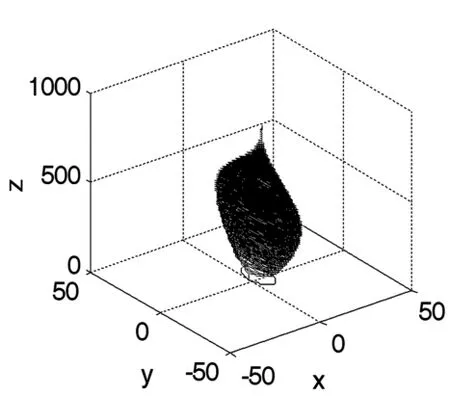
图1 奇怪吸引子(q=-50)Fig.1 Strange attractors(q=-50)
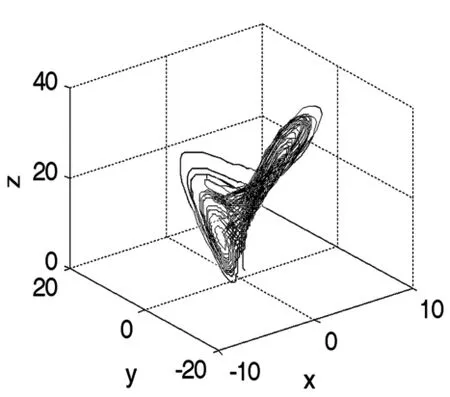
图2 奇怪吸引子(q=-1)Fig.2 Strange attractors(q=-1)
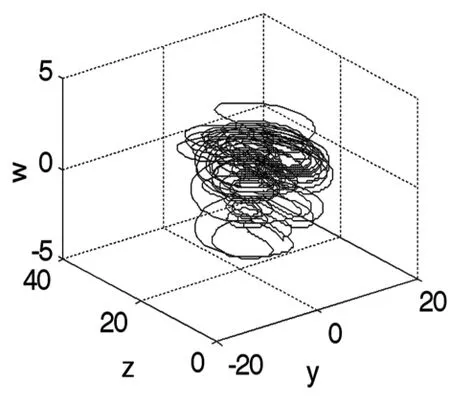
图3 奇怪吸引子(q=-0.5)Fig.3 Strange attractors(q=-0.5)
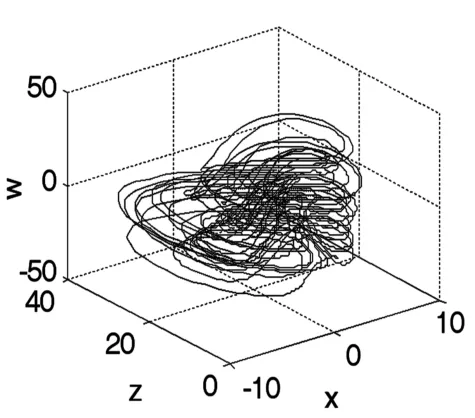
图4 奇怪吸引子(q=10)Fig.4 Strange attractors(q=10)
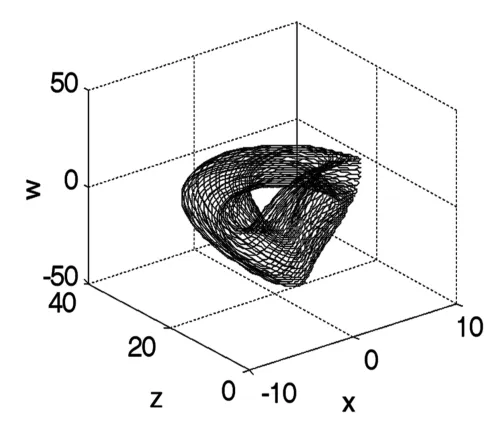
图5 吸引环面(q=35)Fig.5 Attracting torus(q=35)
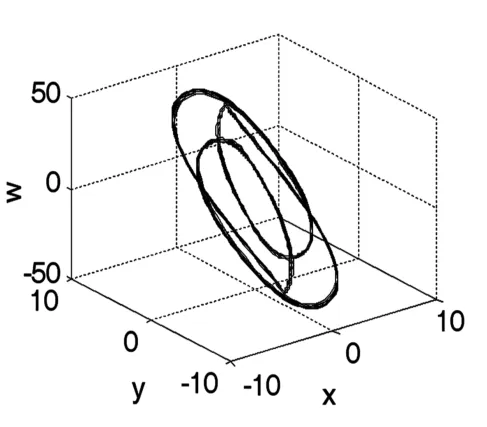
图6 拟周期轨道(q=55)Fig.6 Quasi-periodic orbit(q=55)
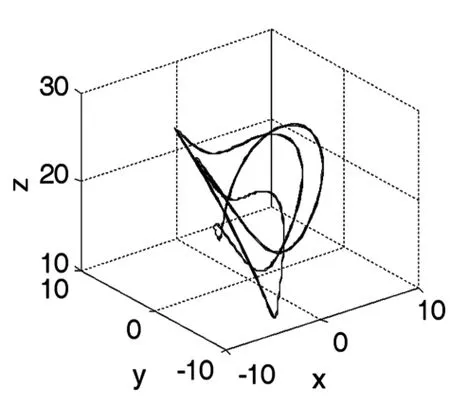
图7 周期轨道(q=56.4)Fig.7 Periodic orbit(q=56.4)
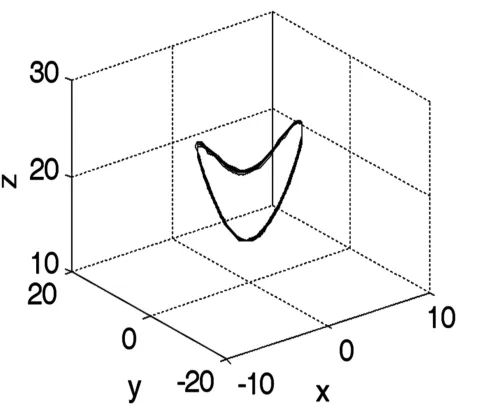
图8 拟周期轨道(q=105)Fig.8 Quasi-periodic orbit(q=105)
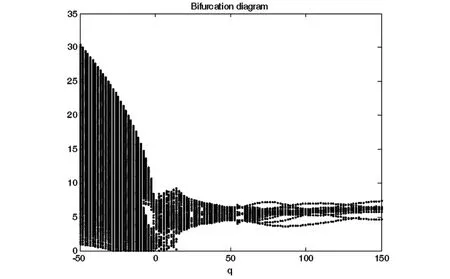
图9 q变化时状态变量x的分岔图Fig.9 Bifurcation diagram of x with increasing q
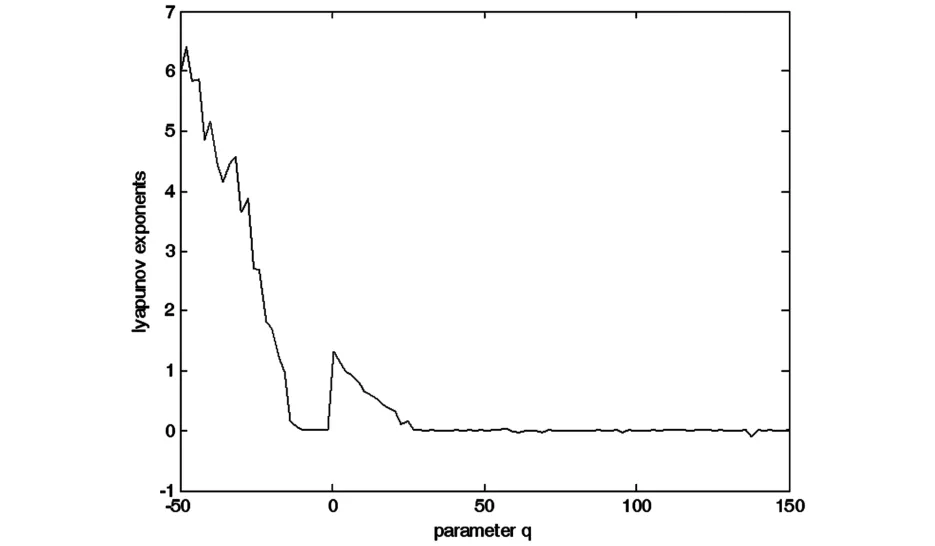
图10 最大Lyapunov指数Fig.10 Maximum Lyapunov exponents
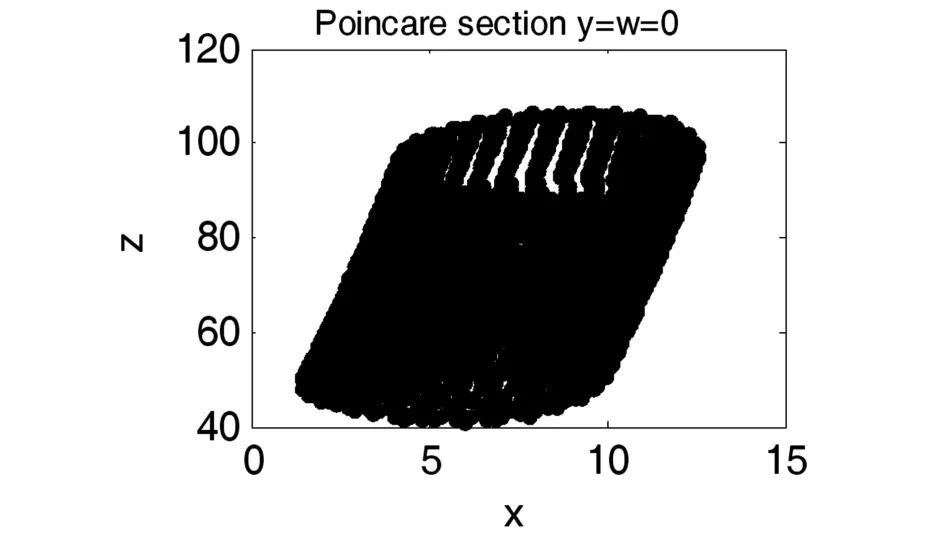
图11 庞加莱映射(q=-5)Fig.11 Poincare map(q=-5)
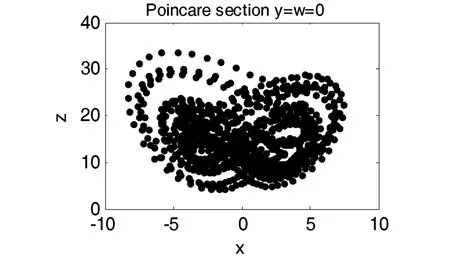
图12 庞加莱映射 (q=120)Fig.12 Poincare map (q=120)
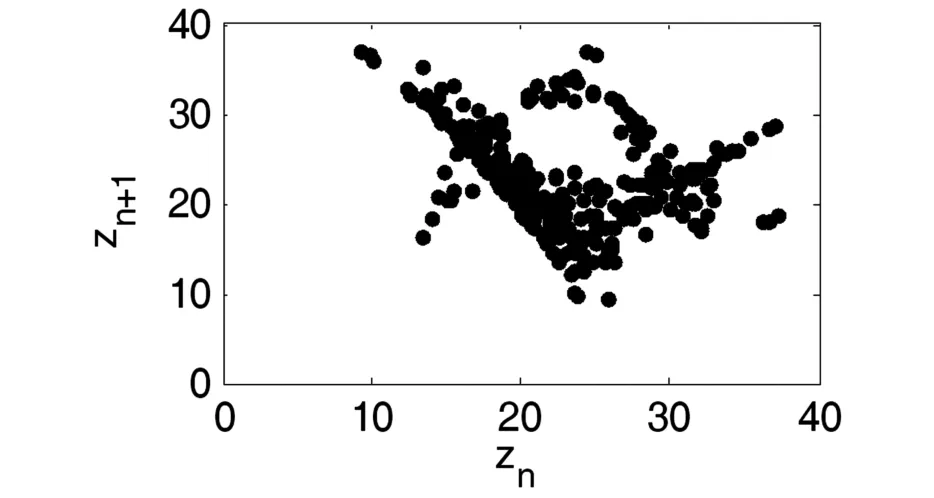
图13 返回映射(q=8)Fig.13 Return map(q=8)
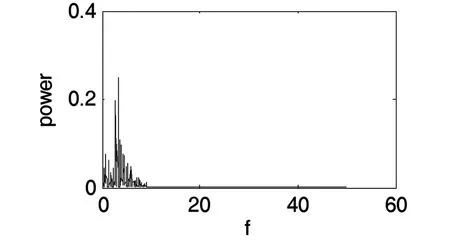
图14 功率谱(q=8)Fig.14 Power spectrum(q=8)
这些结果表明新超混沌系统的动力学行为与超混沌刘系统非常不同,因此,这个超混沌系统的控制与同步问题尤为重要.
2 超混沌系统的稳定
为了控制带有未知参数的超混沌系统稳定到不稳定的平衡点E0,让我们假设的超混沌系统(1)的动力学方程如下:
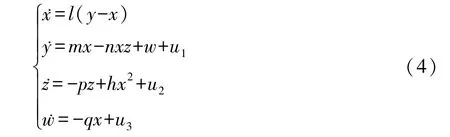
这里 l,m,n,p,q 和 h 是未知参数, u1,u2,u3是设计的控制器.
我们选择如下的Lyapunov函数:

V沿系统(4)的轨线关于时间的导数为:
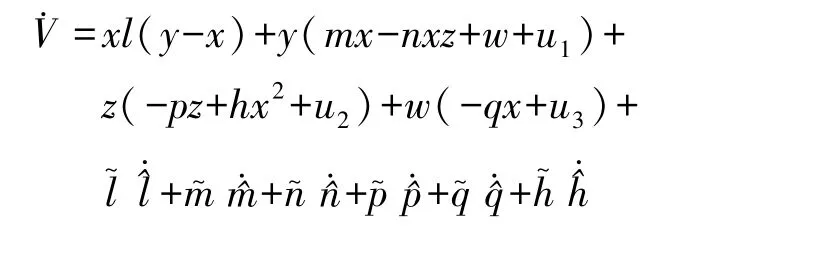
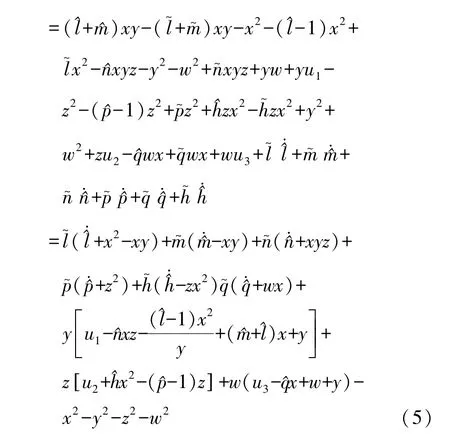
控制器 u1,u2,u3选择如下:
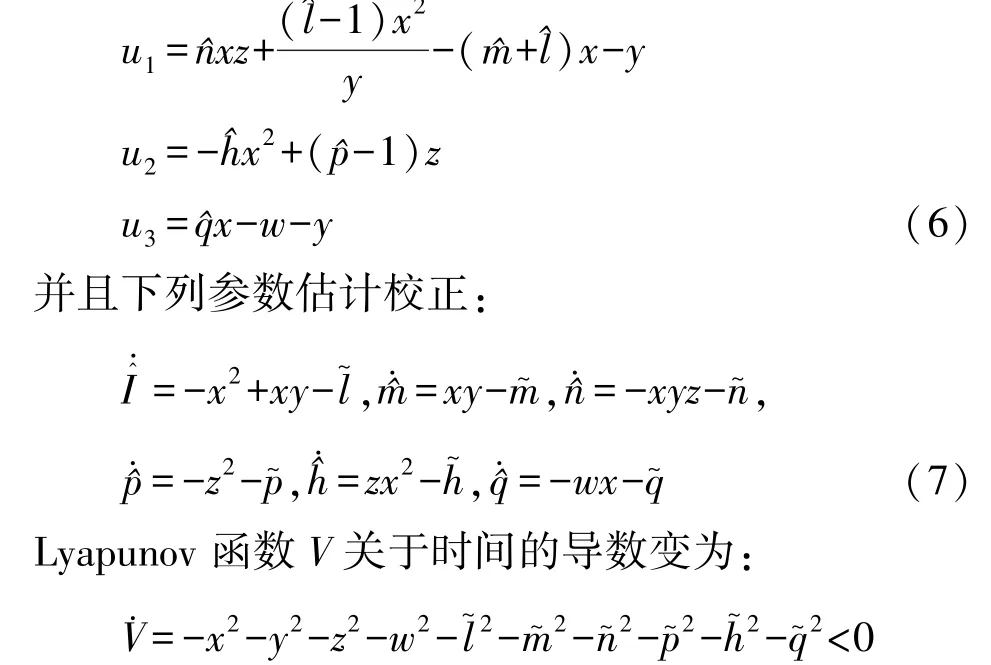
显然在系统(4)零解的邻域内V是正定的,并且V·负定的,因此,基于Lyapunov稳定性理论,利用控制器(6)和参数估计校正律(7),控制系统(4)能渐近收敛到不稳定平衡点 E0(0,0,0,0).
3 超混沌系统的同步
这一部分,基于Lyapunov稳定性理论和自适应控制理论,我们实现两个相同具有未知参数的超混沌系统之间的同步.驱动系统和响应系统分别如下:
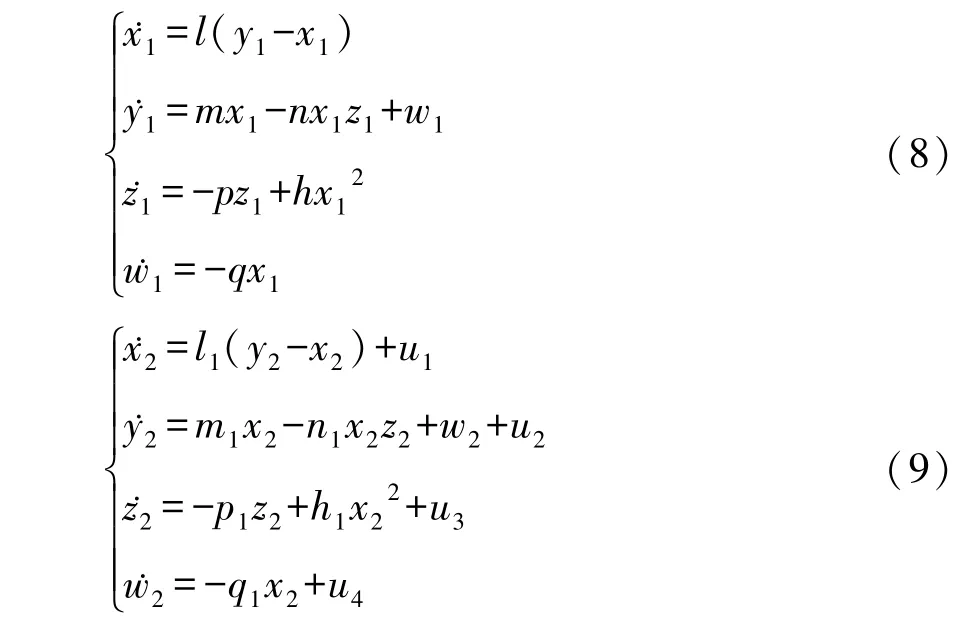
其中 l,m,n,p,q,h 是驱动系统的未知参数, l1,m1,n1,p1,q1,h1是响应系统需要估计的未知参数, u1,u2,u3和u4是设计使得两个超混沌系统相互同步的控制器.
响应系统(9)减驱动系统(8)得到下列误差系统:
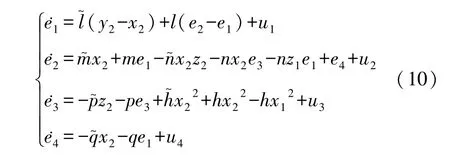
其中 e1=x2-x1,e2=y2-y1,e3=z2-z1,e4=w2-w1,并且h1-h.
控制目标是找到方程(10)的控制器和参数估计校正律,使得驱动系统和响应系统的彼此状态达到全局渐近同步,我们得到如下结论.
定理构造自适应控制器

则驱动系统(8)和响应系统(9)将全局同步.
证明选择下列Lyapunov函数:
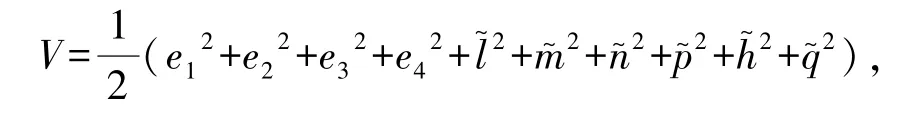
Lyapunov函数沿方程(10)的解关于时间的导数为:
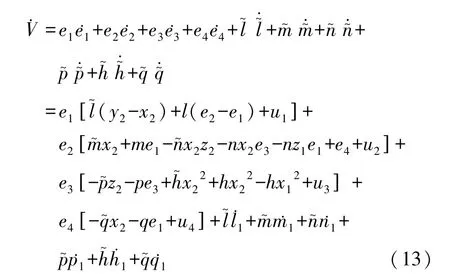
把(11)和(12)代入(13) 得:
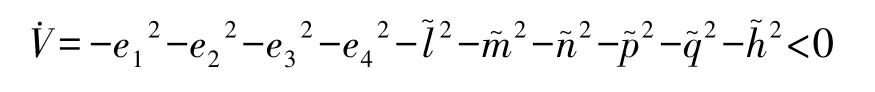
类似的,由于V为正定函数,V·负定的,在控制器(11)和参数估计校正律(12)下,驱动系统(8)和响应系统(9)将达到全局渐近同步.
4 数值模拟
这一部分,我们采用四阶龙格-库塔方法给出了一些数值算例,以验证所提出方法的有效性.在数值模拟中,时间步长取0.001,参数选择l=8,m=25,n=2,p=4,h=5,q=18以确保超混沌系统(1)存在混沌.
算例 1控制超混沌系统(1)到平衡点 E0(0,0,0,0)
在图15中我们注意到系统(1)的状态变量x,y,z,w是不稳定的,但是当施加控制器 U=[u1u2u3]T, 图16显示混沌系统在初始条件(x(0),y(0),z(0),w(0))= (2,2,2,-2)很快驱使到原点,而且误差估计为
同时, 在图 17 中我们能看到当t→∞时控制器是有界的.
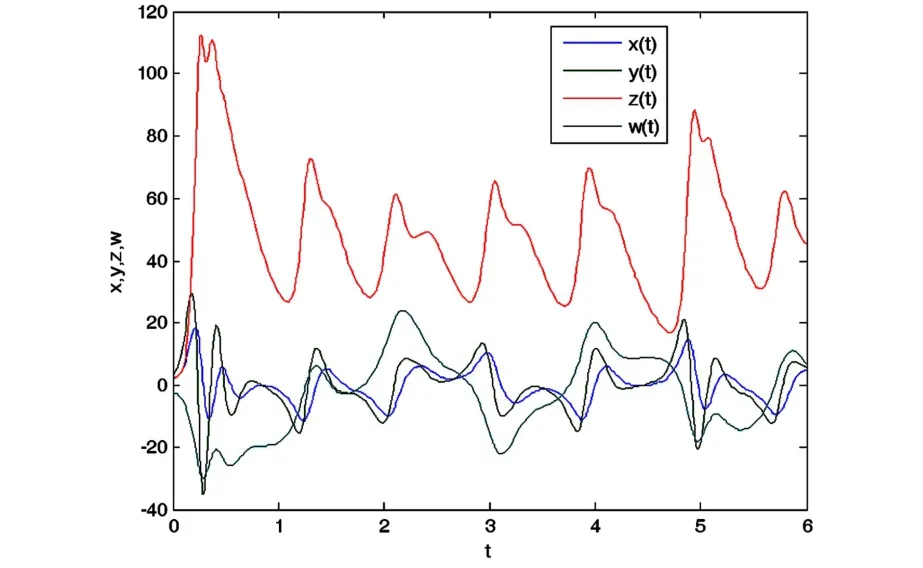
图15 不施加控制器U系统(1)的状态变量x,y,z,w的变化状态Fig.15 State of variable x,y,z,wof the system (1)without control law U
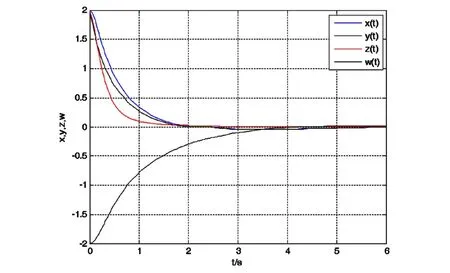
图16 状态变量(x,y,z,w)的时间响应Fig.16 Time history of the states (x,y,z,w)
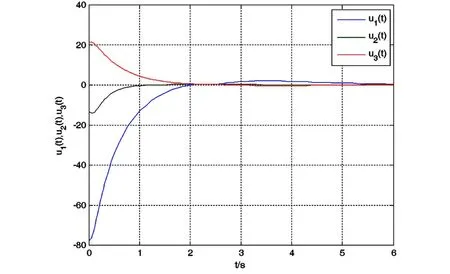
图17 控制器作用 u1(t),u2(t),u3(t) 稳定平衡在 E0Fig.17 Stabilizing equilibrium at E0of control actions u1(t),u2(t),u3(t)
算例2参数未知的超混沌系统的自适应同步
在这个例子的数值模拟中,我们考虑方程(8)和(9)给出的系统.驱动系统和响应系统的初始条件取为(x1(0),y1(0),z1(0),w1(0))= (-1,-1,-1,-1),(x2(0),y2(0),z2(0),w2(0))= (1,1,1,1).因此初始误差为 e1(0)= 2,e2(0)= 2,e3(0)= 2,e4(0)= 2, 不确定的参数选为(l1(0),m1(0),n1(0),p1(0),h1(0),q1(0))= (8,25,2,4,5,18).图 18~20 显示了数值模拟结果,图18显示了驱动系统和响应系统的时间演化,从中我们可以看出起始于不同条件的两个超混沌系统是相互同步的.定义同步误差e(t)=,图19显示了其时间演化,显然误差信号渐近收敛于零.图20显示了当 t→∞ 参数时,l1(t),m1(t),n1(t),p1(t),h1(t),q1(t)的估计值.我们能看到当t→∞ 时不确定参数的估计值收敛于 l=8,m=25,n=2,p=4,h=5,q=18.
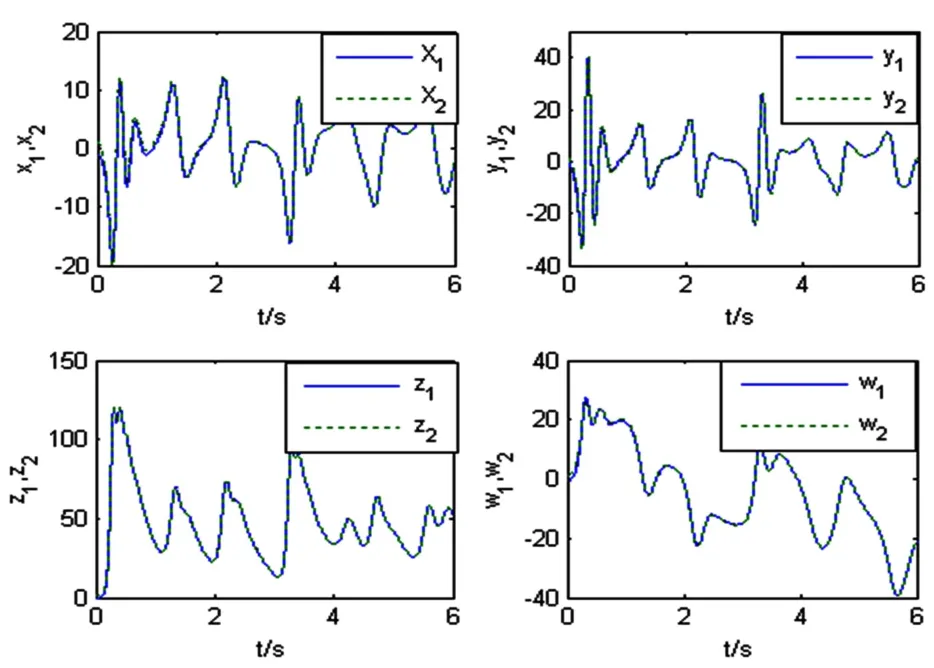
图18 驱动系统和响应系统的状态变量的状态轨线Fig.18 State trajectories of state variables for drive system and response system
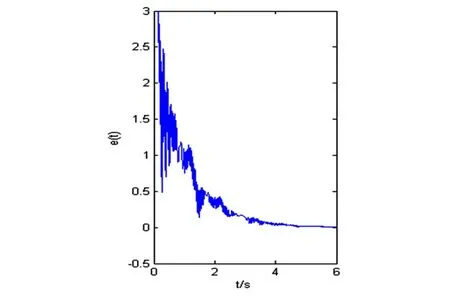
图19 关于时间t的误差e(t)Fig.19 Time history of error e(t)
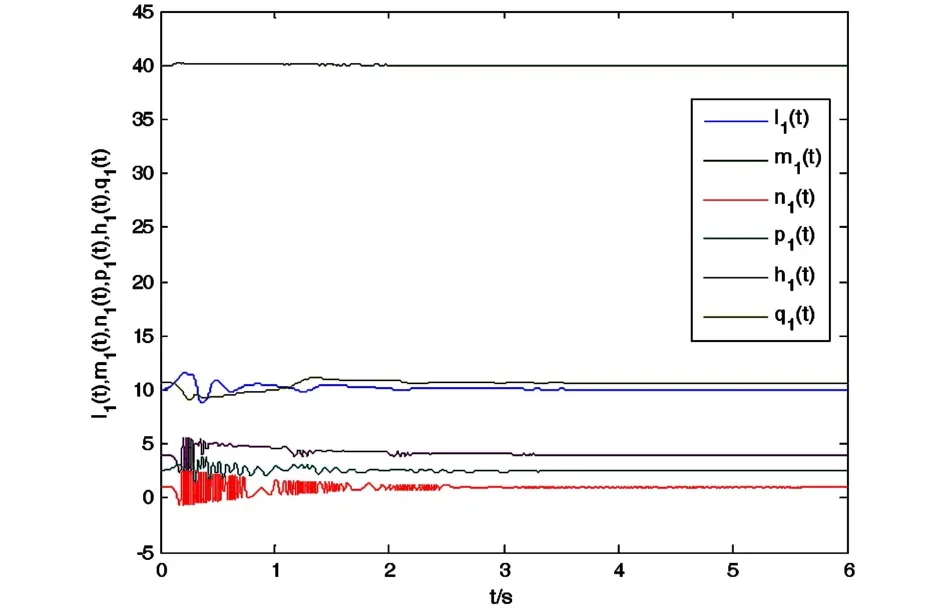
图20 关于时间t的参数估计Fig.20 Time history of parameter estimation
5 结论
本文讨论了一个参数未知的新超混沌系统的动力学行为和数值模拟以及自适应控制与同步问题.基于相图,分岔图、Lyapunov指数谱、庞加莱截面、功率谱和回归映射,在理论上和数值上研究了该混沌系统参数q一定范围内的动力学行为,实现了超混沌系统稳定到不稳定的平衡点.此外,基于Lyapunov稳定性理论和自适应控制理论实现了两个相同的超混沌系统之间的同步.由于超混沌系统具有复杂的动力学行为,因此,通过自适应控制技术实现的超混沌系统同步是有实际意义的.
1 Yu X.Controlling Lorenz chaos.International Journal of Systems Science, 1996,27(4):355~359
2 Zhong Q L,Shao Y H, Zheng Y G.Active sliding mode synchronization of fractional order chaotic systems.Journal of Dynamics and Control, 2015,13(1):18~22
3 Carroll T L,Perora L M.Synchronizing a chaotic systems.IEEE Transactionon Circuits Systems, 1991,38:453~456
4 Oketami N T, Ushio T, Hirai K.Decentralized control of chaos in nonlinear networks.Physics Letters A, 1995,198(4):327~332
5 Wu C, Yang T, Chua L O.On adaptive synchronization and control of nonlinear dynamical systems.International Journal Bifurcation Chaos, 1996,6(3):455~472
6 Cuomo K M,Oppenheim A V.Circuit implementation of synchronizing chaos with applications to communications.Physical Review Letters, 1993,71(1):65~68
7 Chen X Y,Lu J F.Adaptive synchronization of different chaotic systems with fully unknown parameters.Physics Letter A, 2007,364(2):123~128
8 Gao B J,Lu J A.Adaptive synchronization of hyperchaotic lü system with uncertainty.Chinese Physics, 2007,16(3):666~670
9 Rakkiyappan R,Sivasamy R,Lakshmanan S.Exponential synchronization of chaotic Lur′e systems with time-varying delay via sampled-data control, Chinese Physics B, 2014,23(6):0605041-14
10 Wu Y Q,Su H Y,Wu Z G.Asymptotical synchronization of chaotic Lur′e systems under time-varying sampling.Circuits, Systems, and Signal Processing, 2014,33(3):699~712
11 Ge C,Li Z G,Huang X H,et al.New globally asymptotical synchronization of chaotic systems under sampled-data controller.Nonlinear Dynamics, 2014,78(4):2409~2419
12 Wang J, Gao J F, Ma X K.Synchronization control of cross-strict feedback hyperchaotic system based on cross active backstepping design.Physics Letters A, 2007,369(5):452~457
13 Dou F Q,Sun J A,Duan W S,et al.Controlling hyperchaos in the new hyperchaotic system.Communications in Nonlinear Science and Numerical Simulation, 2009,14:552~559
14 Yan Z.Controlling hyperchaos in the new hyperchaotic Chen system.Applied Mathematics& Computation, 2005,168(2):1239~1250
15 Feng X Q,Shen K.Controlling hyperchaos and periodic synchronization in DOPO with parameter modulated by external periodic signal.Chaos Solitons and Fractals, 2008,35(3):506~511
16 Jia Q.Adaptive control and synchronization of a new hy-perchaotic system with unknown parameter.Physiscs Letters A, 2007,362:424~429
17 Zhang H,Ma X K,Li M,et al.Controlling and tracking hyperchaotic Rössler system via active backstepping design.Chaos Solitons and Fractals, 2005,26(2):353~361
18 Chen A, Lu J, Lü J, et al.Generating hyperchaotic Lü attractor via state feedback control.Physica A, 2006,364:103~110
19 Jia Q.Hyperchaos generated from the Lorenz Chaotic system and its control.Physics Letters A, 2007,366(3):217~222
20 Yan Z,Yu P.Hyperchaos synchronization and controlon a new hyperchaotic attractor.Chaos Solitons and Fractals,2008,35(2):333~345
21 Li C,Liao X,Wong K W.Lag synchronization of hyperchaos with applications to secure communications.Chaos Solitons and Fractals, 2005,23:183~193
22 Yassen M T.Synchronization hyperchaos of hyperchaotic systems.Chaos Solitons and Fractals.2008,37(2):465~475
23 Haeri M,Dehghani M.Impulsive synchronization of different hyperchaotic (chaotic) systems.Chaos Solitons and Fractals, 2008,38(1):120~131
24 Rafikov M,Balthazar J M.On control and synchronization in chaotic and hyperchaotic systems via linear feedback control.Communications in Nonlinear Science and Numerical Simulation, 2008,13:1246~1255
25 Zou Y L,Zhu J,Chen G,et al.Synchronization of hyperchaotic oscillators via single unidirectional chaotic coupling.Chaos Solitons and Fractals,2005,25(5):1245~1253
26 Jang M J, Chen C L, Chen C K.Sliding mode control of hyperchaos in Rössler systems.Chaos Solitons and Fractals, 2002,14(9):1465~1476
27 Yassen M T.On hyperchaos synchronization of a hyperchaos Lü system.Nonlinear Analysis Theory Methods and Applications, 2008,68(11):3592~3600
28 Wang F Q,Liu C X.Hyperchaos evolved from the Liu chaotic system.Chinese Physics, 2006,15(5):963~968
DYNAMICAL BEHAVIORS OF A NEW HYPERCHAOTIC SYSTEM AND ITS ADAPTIVE CONTROL AND SYNCHRONIZATION∗
Wang Heyuan†Yin Xia
(College of Sciences, Liaoning University of Technology, Jinzhou 121001, China)
This paper examines the hyperchaotic dynamical behaviors of a new chaotic system,and the numerical simulation results of the adaptive control and synchronization problems of the hyperchaotic system with unknown parameters are presented.The chaotic behaviors of the hyperchaotic system is investigated by detailed numerical simulations results, such as phase portraits, Lyapunov exponents, bifurcation diagrams, and Poincaré sections,power spectrum and return map.Base on the Lyapunov stability theory we derive the adaptive control law that the trajectory of the hyperchaotic system with unknown parameters can be globally stabilized to an unstable equilibrium point of the uncontrolled system.In addition,the adaptive control law is also applied to achieve the state synchronization of two identical hyperchaotic systems.Moreover,the simulation results eventually indicate the validity of the proposed techniques.
hyperchaotic system, chaos control, synchronization, Lyapunov stability theory
26 December 2015,revised 1 October 2016.
10.6052/1672-6553-2017-002
2015-12-26收到第1稿,2016-10-01收到修改稿.
∗国家自然科学基金资助(11572146,11526105)
†通讯作者 E-mail:wangheyuan6400@sina.com
∗The project supported by the National Natural Science Foundation of China(11572146, 11526105)
†Corresponding author E-mail:wangheyuan6400@sina.com

