中心刚体-柔性梁应变反馈多目标优化控制∗

余瑶 文浩陈提

（南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

中心刚体-柔性梁应变反馈多目标优化控制∗

余瑶 文浩†陈提

（南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

本文针对柔性结构在轨组装任务背景，将自动飞船和待运送部件分别简化为中心刚体和柔性梁附件，研究自由漂浮中心刚体-柔性梁系统的动力学与控制问题.首先基于小变形和低转速假设，将梁用假设模态法离散，采用Lagrange方程导出系统动力学方程.继而设计一种带有应变反馈的PD控制律用于完成中心刚体的状态镇定以及柔性梁振动抑制.此外，本文还使用遗传算法对控制器中的参数进行多目标优化.最后，通过数值算例验证了所设计控制器的有效性.

中心刚体-柔性梁， 刚柔耦合， 遗传算法， 多目标优化， 应变反馈

引言

随着航天技术的发展，航天器逐渐大型化、轻质化.由于受到航天运载器单次运载能力的限制，如何构建这些大型航天结构是当前学术界和工程界关注的热点.在轨组装技术是一种非常具有吸引力的大型航天器建造方法［1］.Peggy等展示了如何通过自由飞行的空间机器人完成柔性空间结构的运输、装配以及振动控制［2］.Chen等针对多个中心刚体-柔性梁构成的一组欠驱动拉格朗日系统，将输出一致控制器和避撞控制器结合设计了组装过程复合控制律［3］.

柔性空间结构在轨组装首先需通过自动飞船或空间机器人将柔性部件运送至待组装地点.在此过程中，刚体的运动会引起柔性附件的振动，同时柔性附件的振动也会影响刚体的运动，两者相互耦合.刚柔耦合系统动力学与控制是学术界和工程界广泛关注的重要问题［4］.例如，Tso等采用 Lagrange方程和假设模态法建立了柔性机械臂的动力学模型，并利用挠度反馈对柔性机械臂的振动进行了控制［5］.Cai等使用Hamilton原理建立了中心刚体-柔性梁系统的一次近似耦合模型，并研究了系统在不同阻尼情况下的动力学特性［6］.Bakhti和Idrissi考虑柔性梁小变形情况下的中心刚体-柔性梁系统的旋转运动，提出了一种基于模型的多变量预测控制器，结合卡尔曼滤波器实现了状态反馈振动控制［7］.Feliu等提出了一种针对单个柔性臂的应变反馈无源控制器设计方法，研究了大负载变化情况下柔性梁末端的精确定位问题［8］.Wu等建立了带柔性附件航天器的三维动力学模型，为航天器在障碍物环境中的位置和大角度操纵提出了避障控制方案［9］.

值得注意的是，刚柔耦合系统控制的任务目标往往不是单一的.为了优化多个甚至相互冲突的量，多目标优化技术目前已被广泛应用于控制系统的设计和调节问题中.相对于传统的单目标优化问题，多目标问题的解是由许多满足条件的解组成的解集，称之为Pareto集，相应的由目标函数值组成的集称之为 Pareto前沿［10］.遗传算法、蚁群优化、免疫算法等方法已经成功应用于反馈控制系统的多目标优化设计［11］.例如，Chen等针对旋转柔性梁的跟踪问题设计了PID控制器，并采用胞映射法对超调量和峰值时间等控制变量进行优化设计［12］.Zhang等用将蚁群优化算法用于卫星控制资源的调度问题［13］.Yue等基于遗传算法研究了冗余机械臂的振动抑制和点对点最优轨迹规划问题［14］.Loudini等设计了标准的PD模糊逻辑控制器用于精确控制单个柔性杆的末端位置，并用遗传算法优化了控制器参数［15］.

现有的中心刚体-柔性梁系统动力学与控制研究通常假设刚体中心位置固定，大都不考虑中心刚体平动情况下的动力学特性.本文针对柔性结构在轨组装任务背景，研究由自动飞船或空间机器人将柔性部件运送至待组装地点过程中的位置平动、姿态转动及柔性振动的综合控制问题.为此，本文将自动飞船和待运送部件分别简化为中心刚体和柔性梁附件，建立了自由漂浮的中心刚体-柔性梁系统模型.基于小变形和低转速假设，将梁用假设模态法离散，采用Lagrange方程导出了系统动力学方程.继而设计了一种带有应变反馈的PD控制器，以实现刚体状态镇定和柔性梁振动抑制，并对控制器中的参数进行了多目标优化.最后，通过数值算例验证了所设计控制器的有效性.

1 动力学模型

本文将自动飞船和待运送部件分别简化为圆形中心刚体和柔性梁附件，通过Lagrange方程导出此自由漂浮的中心刚体-柔性梁系统的动力学方程.为便于计算和分析，采用浮动坐标系法描述梁的柔性运动，并通过假设模态法将柔性梁进行离散.如果刚体的转速低，并且梁的变形很小，那么用浮动坐标系建立的系统模型能够足够精确地描述系统的运动且便于控制器的设计［16，17］.

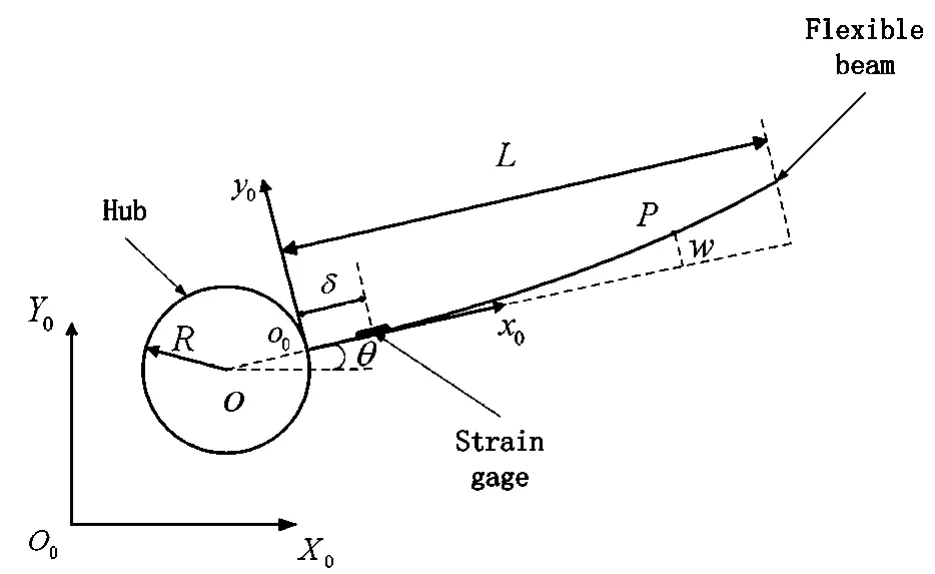
图1 空间自由漂浮的中心刚体-柔性梁示意图Fig.1 Dynamic model of a free-floating hub-beam system

考虑如图1所示在平面内运动的中心刚体-柔性梁系统，其中柔性梁一端固连在中心刚体上．图中O0X0Y0为惯性坐标系，O表示刚体的中心，o0是柔性梁和刚体的连接点，o0x0y0表示固结在未变形梁上的浮动坐标系．为了便于柔性梁的振动抑制，在距离柔性梁固定端x＝δ处粘贴有应变计，其中δ是一个小量．

刚体中心O点在惯性坐标系中的坐标向量表示为 ro＝［X，Y］T，其中 X，Y 分别是刚体中心在 X0，Y0方向上的坐标．此外，θ表示刚体的转角，R表示刚体半径，w表示梁上任意一点P处的挠度．因此P点的位置矢量rP在惯性坐标系O0X0Y0下可以表示为［3］:

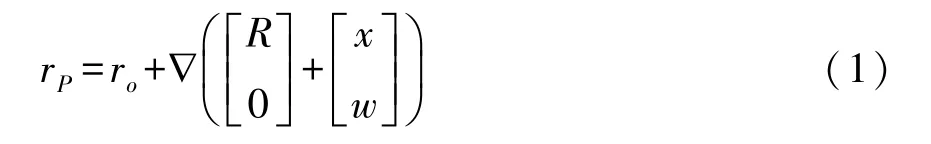
其中∇表示从浮动坐标系转换到惯性坐标系的方向余弦矩阵，具体形式如下:

其中 qi（t）和 φi（x）分别表示悬臂梁的第 i阶模态坐标和第i阶振型函数．不失一般性，仅选取第一阶模态进行控制器设计．在下文中用q和φ表示第一模态坐标和相应振型函数．

系统动能表示为:

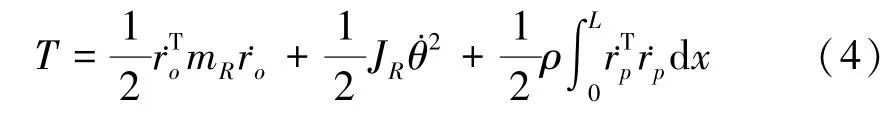
式中mR表示刚体的质量，JR表示刚体的转动惯量，ρ表示柔性梁的线密度．采用Euler梁建模假设，将系统的势能表示为:

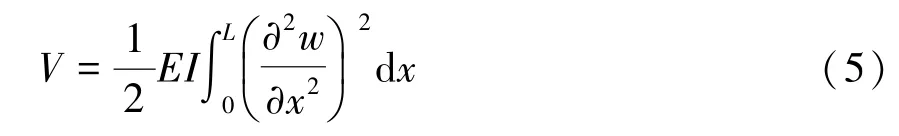
其中E表示材料的弹性模量，I表示柔性梁截面惯性矩．不计系统内阻尼，选取q＝［X Y θ q］T为系统的广义坐标向量，采用拉格朗日方程导出如下系统动力学方程:

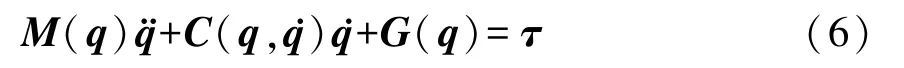
式中M为4×4维惯性矩阵，G＝∂V／∂q为弹性力向量，τ＝［τ1，τ2，τ3，τ4］T为系统的外部控制输入．此外，选取C使得˙M-2C为反对称矩阵．M、C和G的具体表达式见附录．

2 控制律设计

为便于物理实现，假设控制输入仅作用于刚体自由度，模态自由度控制力τ4恒为零．本文采用带有应变反馈的PD控制器使系统姿态达到目标状态，并通过中心刚体与柔性梁间的动力学耦合来实现振动抑制．距离柔性梁的固定端距离δ处的表面应变为:

其中，ε是梁在x＝δ处的应变，h是梁的厚度，注意到对于固定边界条件有φ′（0）＝0，结合:

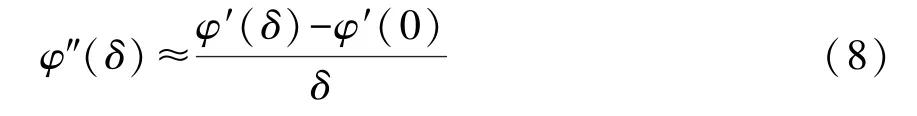
弯曲变形和x＝δ处偏转角α之间的关系为:

由于梁弯曲为小变形，所以α非常小，δ处应变可以表示为［12］:

柔性梁的相对转角α和模态q之间的关系为:

设计如下形式的控制器:

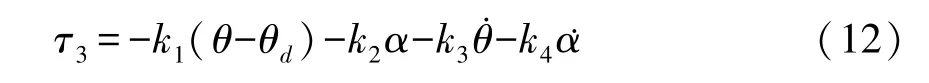
其中 θd为期望达到的姿态角，k1，k2，k3，k4是相应的控制增益．此外，针对系统平动运动设计如下形式的PD控制器:

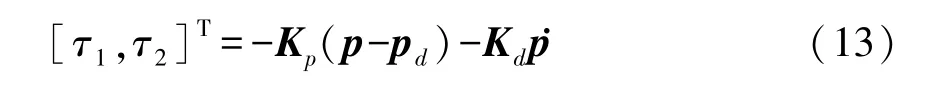
其中p＝［X，Y］T表示刚体当前的坐标位置，pd＝［Xd，Yd］T表示刚体中心预期达到的位置，Kp和Kd均是正定矩阵．

3 多目标优化设计

一般地，多目标优化问题表述为由n个待优化目标函数组成的集合，单个目标函数具有m个相同的决策变量，用数学形式表示为:

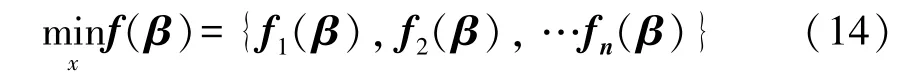
式中， β＝［β1，β2，…，βm］T表示决策向量，包含了m 个决策变量，fi（β）（1≤i≤n）表示目标函数．决策变量的取值空间可表示为:

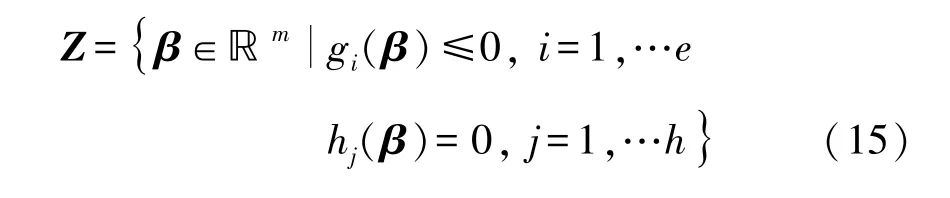
其中e和h分别为不等式和等式约束数，gi和hj分别表示等式约束和不等式约束．

由于每一个目标代表了不同的性能指标，单一的决策向量不可能将全部目标函数同时最优化，因此通常用支配的关系来定义多目标问题的最优解．几个相关定义如下文所示［18］:

定义1 假设向量V，W∈ℝm，V和W是两个决策向量，对任意的一个目标函数fi（1≤i≤n）都满足 fi（V）≤fi（W），且至少有一个 i满足 fi（V）＜fi（W），那么称之为V支配W；

定义2 V是多目标问题的一个可行解，V∈Z，如果在Z中不存在能够支配x的另一个可行解V∗，那么称可行解V是多目标问题的一个Pareto最优解；

定义3 所有Pareto最优解构成的集合称之为Pareto集．

多目标优化的目的就是找到Pareto集，并根据需要选择其中的最优解加以应用．

由于柔性梁横向振动主要与中心刚体转动耦合，因此仅对旋转自由度控制律增益进行优化，将式 （12）中的增益向量 k＝［k1，k2，k3，k4］作为多目标优化的决策向量．超调量和调节时间是单位阶跃响应的重要动态性能指标，用超调量评价系统的阻尼程度，调节时间反映了系统的响应速度．控制律设计的目标是:使中心刚体的位置和姿态达到预期目标位置，并尽可能地减少控制超调量σ和调节时间Ts．因此，该多目标优化问题具有4个设计输入参数和2个目标函数，即．具体遗传算法执行流程如图2所示［4］．

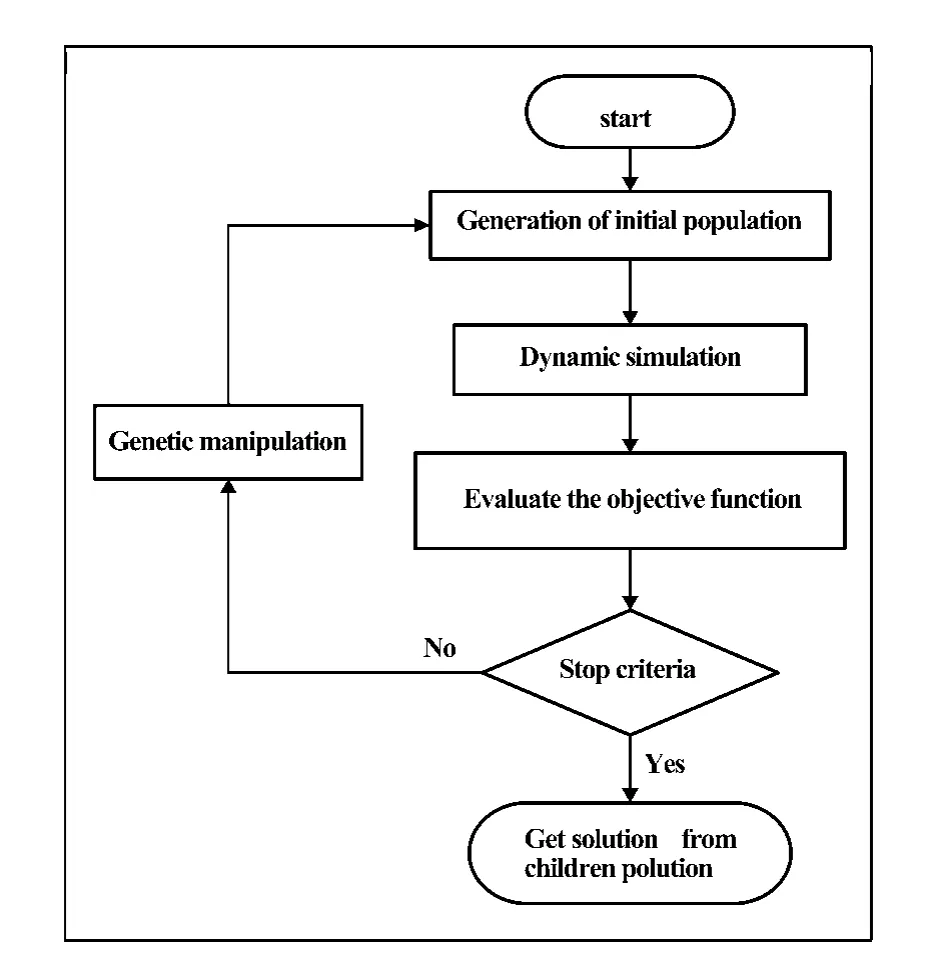
图2 遗传算法优化设计流程图Fig.2 Flow chart of optimization design by genetic algorithm

4 算例仿真

以下通过仿真算例对所述方法进行考核验证．取柔性梁的线密度为 ρ＝0．216kg／m，长度为 L＝2m，弹性模量为 E＝70GPa，截面惯性矩为 I＝2．67×10-11m4，中心刚体质量为mR＝5kg，刚体半径为R＝0．1m，应变计粘贴位置是 δ＝0．02m．

初始时刻柔性梁未产生变形．预期达到的控制目标是将刚体质心位置和转动分别控制到［1，1．5］T和1，其中长度和角度单位分别为米和弧度．为了实现振动抑制目标，柔性梁的相对转角α期望值为 0．选取 Kp＝diag（1，1）和 Kd＝diag（2，2）作为刚体质心位置控制部分的增益．多目标优化设计中，姿态及应变反馈控制增益取值空间设计为:控制目标设计为:

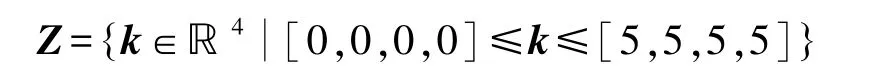
｛σ，Ts｝≤｛10%，10s｝

采用MATLAB遗传算法工具箱的gamultiobj函数实现优化计算．最优前端体系数取为0．6，种群大小设置成1000，最大进化代数为200，停止代数为200，得到4维空间的最优解集．图3和图4是优化增益k的子空间图．

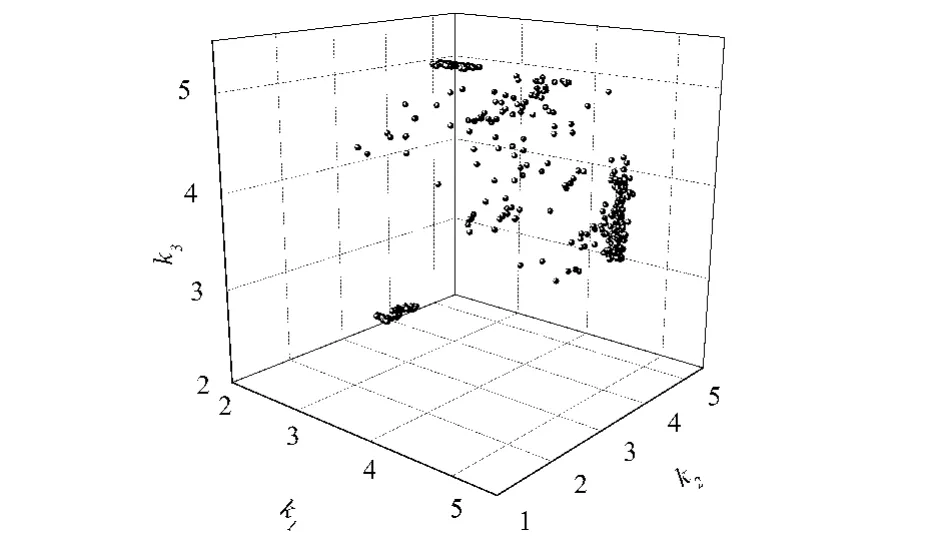
图3 Pareto 集的三维子空间（k1，k2，k3）Fig.3 3D sub-space （k1，k2，k3） of the Pareto set

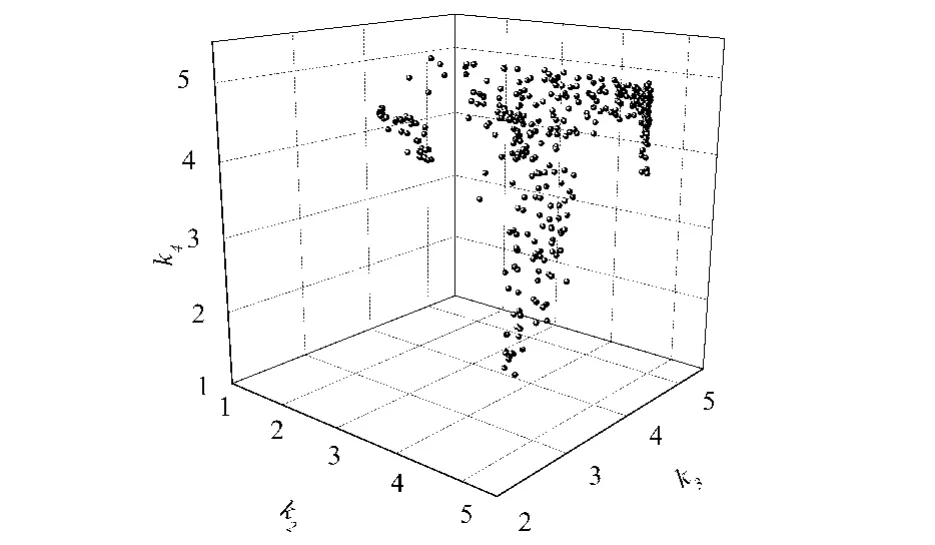
图4 Pareto 集的三维子空间（k2，k3，k4）Fig.4 3D sub-space （k2，k3，k4） of the Pareto set

优化得到的结果均能满足设计的控制目标，即｛σ，Ts｝≤｛10%，10s｝．以下分别对超调量 σ 最小和调节时间Ts最短情形为例进行分析，选择优化结果中对应的控制增益进行仿真．图5和图6给出了转角超调量σ最小情形（算例1）的仿真结果，对应于 k＝［2．2353，4．8386，5．0000，4．4035］时系统的动力学响应．图6是刚体质心的运动轨迹，刚体质心在t＝50s时能够达到预期的位置，图6为刚体的转角θ以及柔性梁相对转角α的时间历程．从图6可以看出，此时跟踪θd产生的转角超调量σ是最小的，几乎为零．

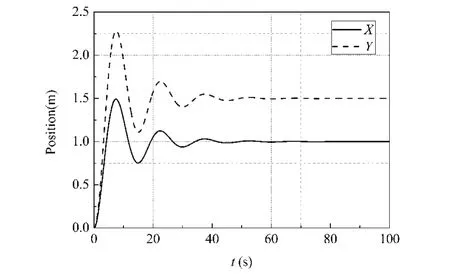
图5 刚体中心位置（算例1）Fig.5 Centroid position of the rigid hub （Case 1）

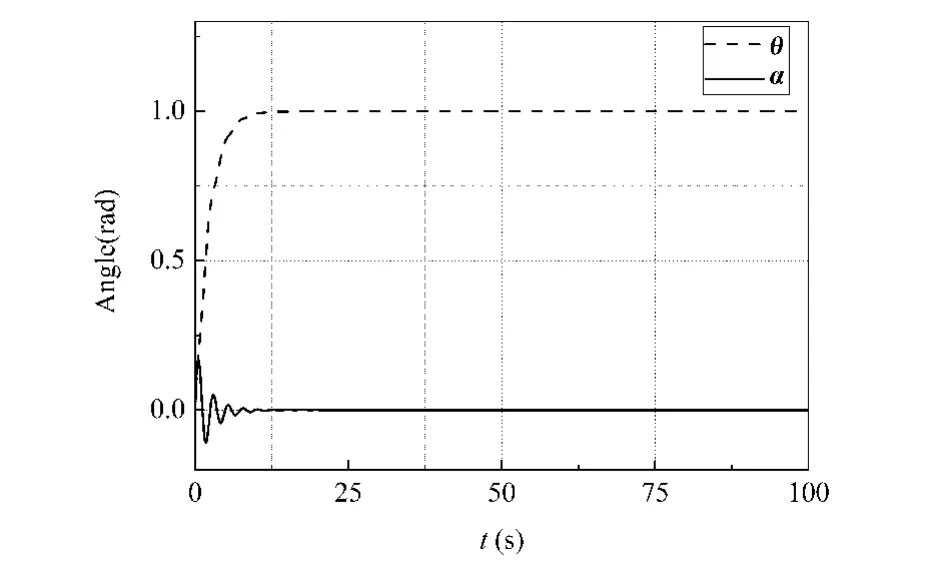
图6 刚体转角θ和柔性梁相对转角α（算例1）Fig.6 Rotation angle θof the hub and relative rotation angle α of the flexible beam

图7和图8给出了调节时间Ts最小情形（算例 2）的仿真结果，即 k＝［2．1068，3．6829，2．1278，4．9120］时系统的动力学响应．对比图5和图7可见，刚体到达预期位置的时间几乎不变．在这组增益的作用下，如图8所示，跟踪θd产生的超调量σ＝2%，然而这种情况下，跟踪θd所需的调节时间较少．仿真结果表明，同一个控制增益不能够同时优化所有的目标函数．

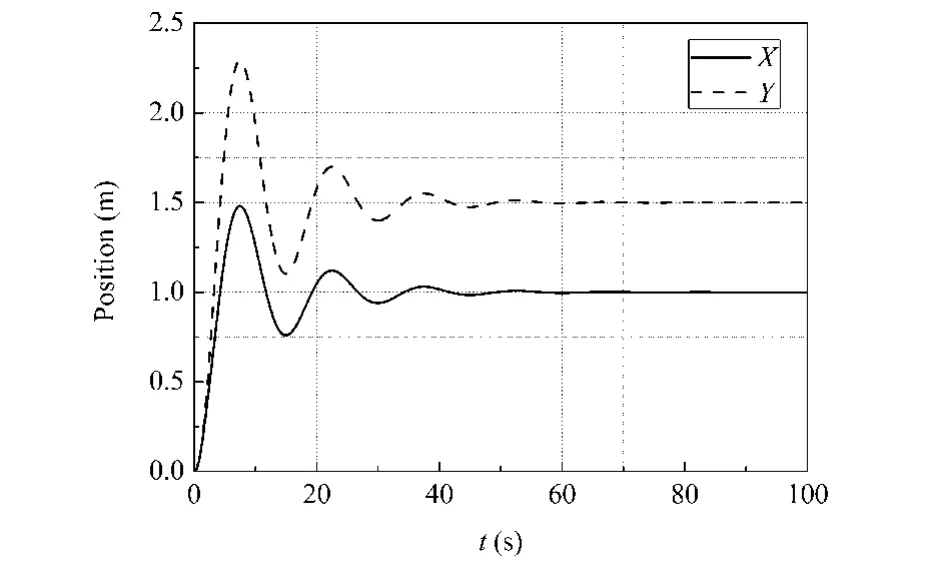
图7 刚体中心位置（算例2）Fig.7 Centroid position of the rigid hub （Case 2）

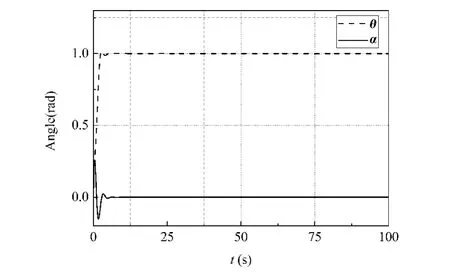
图8 刚体转角θ和柔性梁相对转角α（算例2）Fig.8 Rotation angle θ of the hub and relative rotation angle α of the flexible beam （Case 2）

5 结论

本文考虑柔性构件的在轨运送应用需求，将自动飞船和待运送部件分别简化为圆形中心刚体和柔性梁附件，研究了中心刚体-柔性梁系统的平动、姿态及振动控制问题.为使控制器能够满足特定的性能目标，利用遗传算法求解了带应变反馈的PD控制器的多目标优化问题.在给定的设计空间中，得到了满足相应目标最优的控制增益.仿真结果表明，在给定的设计空间中，存在多个不同的优化增益，不同的增益能达到不同的控制目标.

1 蔡远文，郭会，李岩.航天器在轨组装技术进展.兵工自动化，2009（10）:6～8（Cai Y W，Guo H，Li Y.Development of spacecraft on-orbit assembly technologies.Ordnance Industry Automation， 2009（10）:6～8（in Chinese））

2 Peggy B，Steven D.Coordinated control of space robot teams for the on-orbit construction of large flexible space structures.Advanced Robotics， 2010，24（3）:303～323

3 Chen T，Wen H，Hu H，et al.Output consensus and collision avoidance of a team of flexible spacecraft for on-orbit autonomous assembly.Acta Astronautica， 2016，121:271～281

4 Rahimi H N，Nazemizadeh M.Dynamic analysis and intelligent control techniques for flexible manipulators:A review.Advanced Robotics， 2014，28（2）:63～76

5 Tso S K，Yang T W，Xu W L，et al.Vibration control for a flexible-link robot arm with deflection feedback.International Journal of Non-Linear Mechanics， 2003，38（1）:51～62

6 Cai G P，Lim C W.Dynamics studies of a flexible hubbeam system with significant damping effect.Journal of Sound and Vibration， 2008，318（1）:1～17

7 Bakhti M，Idrissi B B.Active vibration control of a flexible manipulator using model predictive control and kalman optimal filtering.International Journal of Engineering Science and Technology， 2013，5（1）:165～177

8 Feliu V， Pereira E， Díaz I M.Passivity-based control of single-link flexible manipulators using a linear strain feedback.Mechanism and Machine Theory， 2014，71（1）:191～208

9 Wu X，Wen H，Chen T.Manoeuvres of spacecraft with flexible appendage in obstacle environment.International Journal of Space Science and Engineering， 2015，3（1）:16～30

10 Gambier A，Badreddin E.Multi-objective optimal control:An overview.14th IEEE International Conference on Control Applications.Singapore， October 1-3， 2007

11 肖晓伟，肖迪，林锦国等.多目标优化问题的研究概述.计算机应用研究， 2011，28（3）:805～808（Xiao X W，Xiao D， Lin J G，et al.Overview on mulit-optimization problem research.Application Research of Computers，2011，28（3）:805～808 （in Chinese））

12 Chen L X，Sun J Q.Multi-objective optimal design and experimental validation of tracking control of a rotating flexible beam.Journal of Sound and Vibration， 2014，333（19）:4415～4426

13 Zhang N，Feng Z R，Ke L J.Guidance-solution based ant colony optimization for satellite control resource scheduling problem.Applied Intelligence， 2011，35（3）:436～444

14 Yue S，Henrich D，Xu W L，et al.Point-to-Point trajectory planning of flexible redundant robot manipulators u-sing genetic algorithms.Robotica， 2002，20（3）:269～280

15 Loudini M.Modelling and intelligent control of an elastic link robot manipulator.International Journal of Advanced Robotic Systems， 2013，10（1）:257～271

16 Cai G P，Lim C W.Active control of a flexible hub-beam system using optimal tracking control method.International Journal of Mechanical Sciences， 2006，48（10）:1150～1162

17 李莉，刘铸永，洪嘉振.中心刚体-柔性梁刚柔耦合动力学模型降阶研究.动力学与控制学报，2015，13（1）:6～10（Li L ，Liu Z Y ，Hong J Z.Model redution of rigidflexible coupling dynamics of hub-beam system.Journal of Dynamics and Control， 2015，13（1）:6～ 10 （in Chinese））

18 钱伟懿，李阿军，杨宁宁.基于混沌的多目标粒子群优化算法.计算机工程与设计，2008，29（18）:4794～4796（Qian W Y， Li A J， Yang N N.Particle swarm optimization algorithm based on chaotic series for multi-objective optimization problems.Computer Engineering and Design，2008，29（18）:4794～4796 （in Chinese））

附录

MULTI-OBJECTIVE OPTIMAL CONTROL OF A FLEXIBLE HUB-BEAM WITH STRAIN FEEDBACK∗

Yu Yao Wen Hao†Chen Ti
（State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China）

For the application of automatically assembling flexible space structures，this paper studies the dynamic characteristic and control design of a free-floating hub-beam system，where the rigid hub and flexible beam are the simplified models of a spacecraft and a flexible element，respectively.Based on the assumption of small deformation and low motion speed，the beam is discretized through the assumed mode method.The dynamic formulation of the system is derived by using the Lagrange equation.A PD control law with strain feedback is then designed for simultaneously tracking the desired attitude angle and suppressing the vibration of the flexible beam.Moreover，the multi-objective genetic algorithm is applied to perform the multi-objective optimization for the controller parameters.Finally，the effectiveness of the controller is verified by numerical examples.

flexible hub-beam， rigid-flexible coupling， genetic algorithm， multi-objective optimization，strain feedback

22 July 2016，revised 20 December 2016.

10.6052／1672-6553-2017-012

2016-07-22收到第1稿，2016-12-20收到修改稿.

∗国家自然科学基金资助项目（11372130，11290153）和高等学校全国优秀博士论文作者专项资金资助项目（201233）

†通讯作者 E-mail:wenhao＠nuaa.edu.cn

∗The project supported by the National Natural Science Foundation of China（11372130，11290153） and the Foundation for the Author of National Excellent Doctoral Dissertation of China （201233）

† Corresponding author E-mail:wenhao＠nuaa.edu.cn