平移、旋转在初中数学中的应用

孔伟伟

摘 要：“图形的变换”包括图形的轴对称、平移、旋转、相似四种，其中轴对称、平移、旋转同属于全等变换，利用这个特性可以探索基本图形的性质，其同样在初中数学解题中也起着不可替代的作用，可以培养学生“变化”的思维。

关键词：平移变换；旋转变换；四边形；实际问题

波利亚说过：“对一个数学问题，改变它的形式，换一种叙述方式，变换它的结构，直到发现有价值的东西，这是解题的一个重要原则。”《义务教育数学课程标准》也指出几何变换是几何也是整个数学中很重要的内容，它既是学习的对象，也是认识数学的思想和方法。变换又可以看作运动，让图形动起来是指在认识这些图形时，在头脑中让图形动起来。例如，平行四边形是一个中心对称图形，可以把它看作一个刚体，通过围绕中心（两条对角线的交点）旋转，认识、理解、记忆平行四边形的其他性质。充分利用变换认识、理解几何图形，是培养几何直观的好办法。

一、平移变换

经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行且相等。如要寻找几个角之间的关系，可添加平行线使要证的角转换为同位角、内错角或构建全等三角形。

例1：如图1所示，已知AB∥CD，分别探索下列四个图形中∠P与∠A、∠C的关系，请你从所得的四个关系中任选一个加以

说明。

分析：本题点P在平行线内部或外部，添加平行线使要证的角转换为同位角、内错角或同旁内角，得到三个角之间的关系。

过点P作PE∥AB，

∵PE∥AB，CD∥AB，

∴PE∥CD（平行于同一条直线的两直线互相平行）

∴∠EPC=∠C（两直线平行，内错角相等）

同理可得∠A=∠APE

∴∠APC=∠APE+∠CPE=∠A+∠C

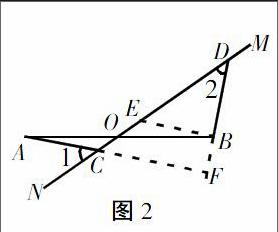
例2：如图2，直线MN与线段AB相交于点O，且OA=OB，∠1=∠2=45°，试探索AC与BD的关系。

分析：本题为“8”字模型，解决这种问题常用的方法为添加平行线BE∥AC，构造全等三角形即△ACO≌△BEO，证得AC=BE，∠ACO=∠BEO，再利用等角的补角相等，从而得到∠1=∠DEB=∠2，根据等腰三角形的判定知BE=BD，故AC=BD。而要确定AC与BD的位置关系，由图可猜想AC⊥BD，故先延长AC、DB交于点F，由∠1和∠DCF为对顶角知∠DCF=45°，在△DCF中，由三角形内角和知∠DFC=90°，故AC⊥BD。

在实际应用中，利用此方法的实际问题也很多，如：在等边△ABC的顶点A、C处各有一只蜗牛，它们同时出发，分别以相同的速度由A向B爬行和沿着BC的延长线爬行，经过t分钟后，它们分别爬行到D、E处，连接DE交AC于点F，则爬行过程中DF与EF始终相等吗？为什么？

二、旋转变换

在旋转这部分中，需要掌握两个图形，很多中考题、中考模拟题都是从这两个图形演变过来的。

类型1：如图3，共顶点的顶角相等的等腰三角形形成旋转全等。在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，则△ABD≌△ACE。

例3：如图4，∠BAC=90°，AB=AC，点D、E在边BC上，且∠DAE=45°，若BD=1，CE=2，求DE的长。

分析：把△ABD绕点A逆时针旋转90°至△ACG，可使AB与AC重合。通过证明△AEG≌△AED得到DE=EG，结合CG=BD，利用勾股定理BD2+EC2=DE2，易得DE=■。

类型2：变换背景：正方形ABCD，旋转△AEB。

例4：如图5，当点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连结EF，则EF=BE+FD，试说明理由。

分析：把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，通过证明∠ADF+∠ADG=180°说明点C、D、G三点共

线，通过证明△AEF≌△AGF，得到EF=FG=FD+DG=DF+BE。

【类比引申1】

如图6，E、F分别运动到边CB、CD的延长线上且∠EAF=45°，连接EF，猜想EF、BE、DF之间的数量关系，并证明。

【类比引申2】

在圖5中，若条件改为“在四边形ABCD中，∠BAD≠90°，

AB=AD，∠B+∠D=180°”，则∠EAF与∠BAD存在 关系时，仍有EF=BE+FD，请证明。

【生活应用】

在图5中将条件改为“在某公园的同一水平面上，四条通道围成四边形ABCD.已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，DF=40■-40，现要在E、F之间修一条笔直道路，则道路EF的长为多少？

总之，在探索几何解题的思路时，可以通过“平移变换”添加平行线，转换角或构建全等三角形，而对于图形具有等边的命题通常可以考虑用旋转变换的思想来解决。它能使分散的已知条件集中起来，化难为易，使一些难题迎刃而解。熟练掌握平移变换和旋转变换思想有助于增强解题能力，开拓思维。因此，教师在教学中应给予足够的重视。

编辑 任 壮