几种SVM的优劣性比较①

尹丽东 范丽亚

( 聊城大学数学科学学院,山东聊城252059 )

几种SVM的优劣性比较①

尹丽东 范丽亚

( 聊城大学数学科学学院,山东聊城252059 )

支持向量机(Support Vector Machine, SVM)是将样本进行分类和回归的一种强大的数学工具，尤其是对高维领域，效果尤为显著.支持向量机工作原理是针对样本数据集，寻找决策函数来对样本数据进行分类的.如今已经衍生出多种SVM的相关模型.最为常见是有孪生支持向量机(T-SVM)，正则化支持向量机(RT-SVM)，最小二乘支持向量机(LSSVM).这几类模型的出发点和建构模型的思想有些许不同之处.本文则选取了三种常见的SVM模型，分析和比较它们之间的优势以及劣势, 能让读者更加深入的了解这类算法, 并且在实际问题中更具有选择应用性.

支持向量机，有效稀疏， 孪生支持向量机，正则化支持向量机

0 引言

目前的时代是一个 “大数据”的时代，当人们谈到“大数据”时候, 首先映入脑海的就是海量的数据和高维的数据，如网络挖掘、网络信息更新、基因表示分析、高频金融数据等.如何能在海量高维的数据中挖掘提取出有用信息,并且利用这些有用信息，来进行数据分析是非常必要的一个研究领域和研究方向, 也是广大研究学者非常关注的一个研究方向..众所周知, 在海量数据中挖掘提取出有用信息，这工作量往往也是非常庞大的, 利用这些有用信息进行数据分析与处理, 一般都会导致算法学习时间过与慢长, 甚至达到失效的结果.而支持向量机(Support Vector Machine, SVM)[1]作为数据监督学习[2]的一个强而有力工具, 为了降低其计算复杂程度, Suykens等人[3]提出了最小二乘SVM (Least Squares SVM, LSSVM).支持向量机，自1995年提出之后, 应用数学的学者们得到了广泛的关注和研究, 并应用于诸多领域, 如人脸检测识别、语音识别、文字手写体识别、图像处理等领域.然而，我们研究发现SVM所具有的稀疏性对于处理大数据和分析问题也是极其重要的.之后，2007年, Jayadeva等人[8]针对二类分类问题提出了孪生SVM(Twin SVM, TSVM), 它是主要思想是解决两个规模较小的二次规划问题，而不是一个大规模的二次规划问题, 从而得到两个非平行超平面, 使每个超平面距离一类尽可能近，而距离另一类尽可能远.TSVM的计算速度比SVM快很多, 通过理论计算推导，其计算速度大约是SVM速度的4倍, 从而大大缩减了算法的学习时间, 对于处理这类海量高维的大数据非常有帮助. 但是TSVM仍然需要求解两个二次规划问题, 当学习的数据样本数据较大时, 仍然有比较高的计算复杂性.为了解决此问题, Kumar等人[9]提出了最小二乘TSVM (Least Squares TSVM, LSTSVM).

接下来的部分,我们对分类器(Support vector classification,SVC)和孪生支持向量机(Twin Support vector Machine,TSVM)等作简要概述和比较研究.

1 支持向量分类(SVC)

考虑二类分类问题的训练集T={(x1,y1),(x2,y2),…,(xm,ym)}，其中xi∈Rn是输入值，yi∈{+1,-1}是对应的输入向量.

线性分类器寻找一个分类超平面

f(x)=wTx+b,

(1)

(2)

其中C>0是参数.使得正则项1/2‖w‖2最小化等价于两个平行的支持超平面wTx+b=1和wTx+b=-1之间的间隔最大化，其中ξi≥0,i=1,…,n为松弛变量,C>0为调节参数. 若令2ξ=(ξ1,…,ξm)T, 则问题(2)可表示为矩阵形式

(3)

考虑问题(3)的Lagrange函数

(4)

进而可构造最优分类超平面〈w*,x〉+b*=0, 使得y=sign(〈w*,x〉+b*).

通过理论推导计算，我们不难发现软间隔SVM的优点，其具有稀疏性，还有较强的推广能力.但这种软间隔支持向量机需要求解一个QPP. 当样本个数m较大时, 无疑会导致计算时间变长.

2 几种SVM型算法及其优势比较

本节主要介绍几种具有代表性的支持向量机, 并且对它们各自的优势和劣势加以分析比较.(注：本节所用符号同上一节).

2.1 孪生支持向量机(T-WSVM)

现考虑如下问题.假定用A∈Rm1×n所有表示正类的数据点,Ai∈Rn表示A的第i行.类似地,用B∈Rm2×n表示负类的数据点.

线性TWSVM寻求一对非平行超平面

f1(x)=w1x+b1=0和f2(x)=w2x+b2=0.

(5)

每一个超平面都逼近其中一类数据点，并且远离另一类,其中w1∈Rn,w2∈Rn,b1∈R,b2∈R.经验风险可以由以下式子来测量

(6)

(7)

其中c1>0和c2>0为参数.通过引入松弛向量ξ,ξ*,η和η*,原始问题可以表示为

(8)

和

(9)

为了得到相应的对偶问题,TWSVM假设HTH和GTG都是非奇异的,其中H=[Ae1],G=[Be2].在此条件下，对偶问题分别是

(10)

和

(11)

为处理HTH和GTG奇异和避免病态的情况, (HTH)-1和(GTG)-1可以分别由(HTH+εI)-1和(GTG+εI)-1来代替,其中I是合适维数的单位阵,ε是一个正标量.因此以上偶对问题可以修改为

(12)

和

(13)

通过

v1=-(HTH+εI)-1GTα和v2=(GTG+εI)-1HTγ

(14)

2.2 最小二乘SVM(LSSVM)

(15)

这样做的目的是加快SVM的学习时间. 显然, 问题(15)可以转化为无约束最优化问题:

(16)

令∂f(w,b)/∂w=∂f(w,b)/∂b=0, 可得

(17)

为不失一般性, 可设对称非负定阵H+CGGT是非奇异阵(否则将其正则化), 于是有

进而可构造最优分类超平面〈w*,x〉+b*=0使得y=sign(〈w*,x〉+b*).

从上述的推导过程中可以得出,LSSVM只需要求解线性方程组(7), 无需求解问题(3), 大大减少了SVM的计算复杂程度, 这是LSSVM的一个较好的优点. 但从问题(6)可以看出,LSSVM又失去了SVM所具有的稀疏性,并且需要求解矩阵H+CGGT的逆矩阵, 当样本的特征个数n较大时, 求解这个逆矩阵，又会花费较长时间, 这就是LSSVM的不足之处.

2.3 正则项支持向量机(RTSVM)

(18)

(19)

考虑模型(18)的wolf对偶形式，考虑其lagrange函数

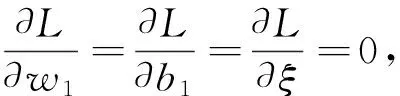
(20)

进而有

(21)

(HTH+I)v1+GTα=0或v1=-(HTH+I)-1GTα,

(22)

将(22)式带入到lagrange函数中，并使用(15)式，得到对偶问题

(23)

同样地，可以得到(16)式的对偶问题

(24)

这里,γ是lagrange乘子,v2=[w2b2]T可以由以下求得

v2=(GTG+I)-1HTγ.

(25)

一旦问题(15)和(16)分别由(20)和(21)得到(w1b1)和(w2b2),一个新的点x∈Rn被分配到类i(i=+1,-1)，它距离(3)中最近的超平面

(26)

2.4L2-SVM

(27)

(28)

令H=[Ae1],G=[Be2],我们得到(27)和(28)的对偶问题

(29)

(30)

一个新的点x∈Rn被分配到类i(i=+1,-1)，它距离(5)中最近的超平面

(31)

3 结论

本文是分析和比较了几种较具代表性的SVM型算法的优劣势,发现了经典的LSSVM虽然降低了SVM的计算复杂程度,但是同时又缺失了SVM所具有的稀疏性特点,而且当样本数量较大时，还需要求解矩阵的逆矩阵,这样又增加了计算复杂性.LSTSVM虽然比LSSVM计算时间快一些, 但我们知道，其同样不具有稀疏性，而且还需要求逆矩阵.所以，SVM学习算法的计算复杂程度和稀疏性对于分析和处理大数据来说，是非常重要的两个因素,特别是对高维数据.为此,学者们对LSSVM和LSTSVM做了改进和推广, 提出了SP-LSSVM,ε-LSSVM,ε-WLSSVM等具有稀疏性的学习算法. 类似于SP-LSSVM,ε-LSSVM和ε-WLSSVM, 针对LSTSVM也可以提出具有稀疏性的学习算法, 因篇幅有限, 本文不再加以具体讨论.

[1] 邓乃扬, 田英杰. 数据挖掘中的新方法: 支持向量机[M]. 北京科学出版社, 2006.

[2]DengNY,TianYJ.SupportVectorMachines:Theory,AlgorithmsandExtensions[M].SciencePress,Beijing, 2009.

[3]SuykensJAK,TonyVG,JosDB,etal.LeastSquaresSupportVectorMachines[M].WorldScientific, 2002.

[4]Suykens,JAKVandewalleJ.Leastsquaressupportvectormachineclassifiers[J].NeuralProcessingLetters, 1999, 9 (3)：293-300.

[5]TianYingjie,JuXuchan,QiZhiquan,etal.Efficientsparseleastsquaressupportvectormachineforpatternclassification[J].ComputersandMachematicswithApplications, 2013, 66：1 935-1 947.

[6]HuangXiaolin,ShiLei,JohanAKS.Asymmetricleastsquaressupportvectormachineclassifiers[J].ComputationalStatisticsandDataAnalysis, 2014, 70：395-405.

[7]XuShuoAnXin,QiaoXiaodong,etal.Multi-outputleast-squaressupportvectorregressionmachines[J].PatternRecognitionLetters, 2013, 34：1 078-1 084.

[8]Jayadeva,KhemchandaniR,ChandraS.Twinsupportvectormachineforpatternclassification[J].IEEETransPatternAnalMachIntell, 2007, 29(5)：905-910.

[9]KumarMA,GopalM.Leastsquarestwinsupportvectormachinesforpatternclassification[J].ExpertSystemsApplications, 2009, 36(4)：7 535-7 543.

[10]YangZhiMin,WuHeJi,LiChunNa,etal.Leastsquaresrecursiveprojectiontwinsupportvectormachineformulti-classclassification[J],InternationalJournalofMachineLearningandCybernetics, 2015, 10：1-16.

[11]ChenWeijie,Shaoyuanhai,DengNaiyang,etal.Laplacianleastsquarestwinsupportvectormachineforsemi-supervisedclassification[J].Neurocomputing, 2014, 145：465-476.

[12]JalalANasiri,NasrollahMOghadamCharkari,SaeedJalili.Leastsquarestwinmulti-classclassificationsupportvectormachine[J].PatternRecognition, 2015, 48：984-992.

[13]GaoShangbing,YeQiaolin,YeNing.1-normleastsquaretwinsupportvectormachines[J].Neurocomputing, 2011, 74：3 590-3 597.

[14] 侯明,张欣欣，范丽亚.四类基于支持向量机的多类分类器的性能比较[J].聊城大学学报：自然科学版, 2014, 27：54-60.

[15] 高西占,范丽亚.基于最小闭球的多类支持向量[J].聊城大学学报：自然科学版, 2014, 26：24-29.

Compare the Advantages and Disadvantages of Several SVM

YIN Li-dong FAN Li-ya

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059,China)

Support Vector Machine (SVM) is a powerful mathematical tool for classification and regression of samples, especially in high-dimensional field. The support vector machine is based on the sample data set and the decision function is used to classify the sample data. Multiple SVM models are now derived. The most common is the twin support vector machine (t-svm), the regularized support vector machine (rt-svm), the least square support vector machine (LSSVM). There are some differences between the starting point and the construction model of these models. In this paper, the selection of the three common SVM model, analyze and compare the advantages and disadvantages between them, could make readers more in-depth understanding of this kind of algorithm, and has more choice applied in the actual problem.

Support Vector Machine, effective sparse, twin support vector machine, regularization support vector machine

2017-03-16

国家自然科学基金项目(11501278);山东省自然科学基金项目(ZR2013AQ011)资助

范丽亚，E-mail:fanliya63@126.com.

O224

A

1672-6634(2017)02-0014-06