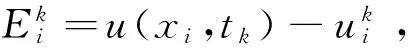二维非线性Klein-Gordon方程Neumann边值问题①
盛秀兰 郝宗艳 吴宏伟
(1.东南大学数学系,江苏南京210096;2.江苏开放大学,江苏南京210036)
二维非线性Klein-Gordon方程Neumann边值问题①
盛秀兰1,2郝宗艳1吴宏伟1
(1.东南大学数学系,江苏南京210096;2.江苏开放大学,江苏南京210036)
利用边界条件及非线性Klein-Gordon方程得到其在空间上的三阶与五阶导数的边界值,进而分别在内点和边界点建立三点和两点紧差分格式;通过数值算例,得到了截断误差是关于时间和空间上的二阶和四阶结果.
非线性Klein-Gordon方程,紧差分格式,边值问题
0 引言
研究如下一维非线性Klein-Gordon方程Neumann的边值问题的数值解,
-utt-(uxx+uyy)+g(u)=f(x,,y,t),x,y∈Ω,0 (1) (2) (3) (4) 其中Ω=(0,1)×(0,1),g(u),f(x,y,t)为光滑函数. Klein-Gordon方程是相对论量子力学和量子场论中用于描述零自旋粒子的自由运动方程,关于它的数值解法已有不少研究结果.文献[1]基于样条基函数提出了一个数值格式.四阶紧格式在文献[2]中进行了研究.基于变分迭代方法的班数值格式及边界元方法可参见文献[3,4]在文献[5]中导出了以三层样条差分格式逼近非线性Klein-Gordon方程.无界域上的问题的数值研究课参见文献[6].文献[7]中提出了一个基于有限差分和匹配法的新的数值格式,而文献[8]提出了微分积分法.所有这些文献中的研究都是针对Dirichlet边界条件,对于Neumann边界条件下的高阶差分格式还没有很好的结果.近年来,具有Neumann边界条件的热方程的高阶差分格式已有一些研究结果[9-11].文献[12]研究了Cahn-Hilliard方程Neumann边界条件下的三层线性化紧格式.最近,文献[13]中建立了哈密尔顿非线性波方程Neumann边界条件下的高阶显格式,该方法空间方向基于紧格式,时间方向基于Runge-Kutta-Nystrom方法. 文献[14]给出了边界点处离散方程的方法. 通过分析以上文献,了解到Klein-Gordon方程Neumann边值问题的无条件稳定的高阶差分格式,目前还没有这方面的结果,其主要困难是边界点的处理.本文利用Klein-Gordon方程及边界条件可得到在边界处的三阶导数和五阶导数的函数值,从而建立边界点和内点处的两点和三点紧差分格式.最后给出了一些数值算例,计算出收敛阶数为O(τ2+h4). 由(1)式中的方程可得 auxx=utt+g(u)-f(x,t), (5) 由(5)式分别求其关于x的k(k=3,4,5)阶导数,且由边界条件可得 (6) (6)式在建立差分格式时起到了重要的作用. 取正整数m,n,记空间步长与时间步长为 引理1[13]记α(s)=(1-s)3[5-3(1-s)2],s∈[0,1]. utt(x,y,t)-v(x,y,t)-w(x,y,t)+g(u(x,y,t))=f(x,,y,t),x,y∈Ω,0 (7) 令 则由算子Α,Β及引理1,可以得到 (8) (9) (10) (11) (12) (13) 由Taylor展开式可知 (14) (15) (16) 将(8)—(13) 、(14)—(16)式代入(7)式,并由引理2可得 (17) (18) (19) (20) (21) (22) 其中该问题的精确解为 f(x,t)=-[x2(x-1)2y2(y-1)2+2x2(x-1)2(6y2-6y+1)+2y2(y-1)2(6x2-6x+1)cost+x4(x-1)4y4(y-1)4cos2t]. 表2 取不同步长时数值解的最大误差 [1]DehghanM,ShokriA.NumericalsolutionofthenonlinearKlein-Gordonequationusingradialbasisfunctions[J].JComputApplMath, 2009, 230(2):400-410. [2]DehghanM,MohebbiA,AsghariZ.Fourth-ordercompactsolutionofthenonlinearKlein-Gordonequation[J].NumericalAlgorithms, 2009, 52(4): 523-540. [3]ShakeriF,DehghanM.NumericalsolutionoftheKlein-GordonequationviaHe’svariationaliterationmethod[J].NonlinearDynamics, 2008, 51(1-2): 89-97. [4]DehghanM,GhesmatiA.ApplicationofthedualreciprocityboundaryintegralequationtechniquetosolvethenonlinearKlein-Gordonequation[J].ComputPhysCommun, 2010, 181 (8):1 410-1 418. [5]RashidiniaJ,MohammadiR.TensionsplineapproachforthenumericalsolutionofnonlinearKlein-Gordonequation[J].ComputerPhysicsCommunications,2010, 181(1):78-91. [6]HanH,ZhangZ.Splitlocalabsorbingconditionsforone-dimensionalnonlinearKlein-Gordonequationonunboundeddomain[J].JComputPhys, 2008, 227(20): 8 992-9 004. [7]LakestaniM,DehghanM.Collocationandfinitedifference-collocationmethodsforthesolutionofnonlinearKlein-Gordonequation[J].ComputerPhysicsCommunications, 2010, 181(8):1 392-1 401. [8]KumarS,JiwariR,VermaA.AnumericalschemebasedondifferentialquadraturemethodfornumericalsimulationofnonlinearKlein-Gordonequation[J].InternationalJournalofNumericalMethodsforHeatFluidFlow, 2014, 24 (7):1 390-1 404. [9]SunZhizhong.CompactdifferenceschemesforheatequationwithNeumannboundaryconditions[J].NumericalMethodsforPartialDifferentialEquations, 2009,25(6):1 459-1 486. [10]LiaoWenyuan,ZhuJianping,KhaliqQM.AFourth-OrderCompactAlgorithmforNonlinearReaction-DiffusionEquationswithNeumannBoundaryConditions[J].NumerMethodsPartialDifferentialEq, 2006, 22(3): 600-616. [11]SunZhizhong.CompactDifferenceSchemesforHeatEquationwithNeumannBoundaryConditions[J].NumerMethodsPartialDifferentialEq, 2009, 25(6): 1 459-1 486. [12]LiJuan,SunZhizhong,ZhaoXuan.AthreelevellinearizedcompactdifferenceschemefortheCahn-Hilliardequation[J].ScienceChina,Mathematics, 2012,55 (4):805-826. [13]LiuChangying,ShiWei,WuXinyuan.Anefficienthigh-orderexplicitschemeforsolvingHamiltoniannonlinearwaveequations[J].AppliedMathematicsandComputation, 2014, 246(c): 696-710. [14] 盛秀兰.Kdv方程的Crank-Nicolson差分格式[J].聊城大学学报:自然科学版,2012,25(4):23-26. [15] 孙志忠.偏微分方程数值解[M].北京:科学出版社, 2004. The Two Nonlinear Klein-Gordon Equation with Neumann Boundary Conditions SHENG Xiu-lan1,2HAO Zong-yan1WU Hong-wei1 (1.School of Mathematics, Southeast University, Nanjing 210096,China; 2.Jiangsu Open University, Nanjing 210036,China) By use of the boundary values of three-order and five-order derivatives, the three points scheme at inside points and two points scheme at boundary points are established respectively. Numerical results are conducted to the truncation error of difference scheme,that is second order in time and fourth order in space. nonlinear Klein-Gordon equation,compact difference scheme,boundary value problem 2017-03-25 国家自然科学基金项目(11671081);江苏省高等职业院校专业带头人高端研修项目(2016GRFX011);江苏开放大学“十三五”规划课题(16SSW-Y-009)资助 盛秀兰,E-mail:113525336@qq.com. O241.82 A 1672-6634(2017)02-0001-061 记号及引理



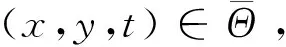
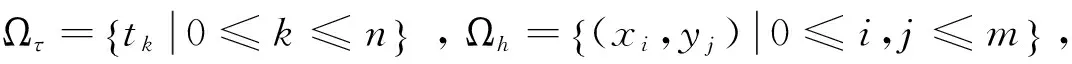
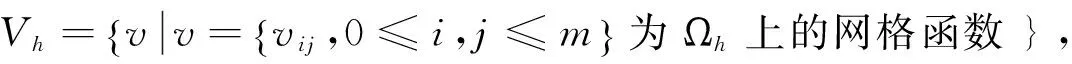
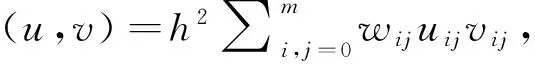

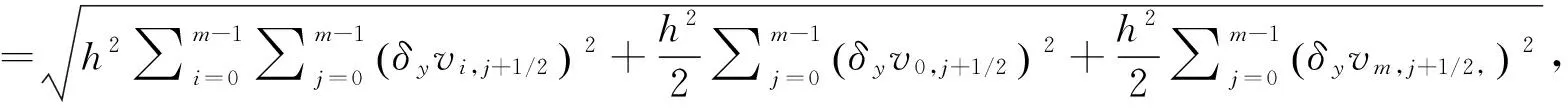




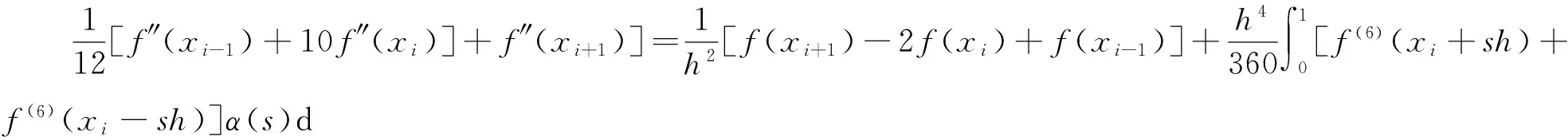
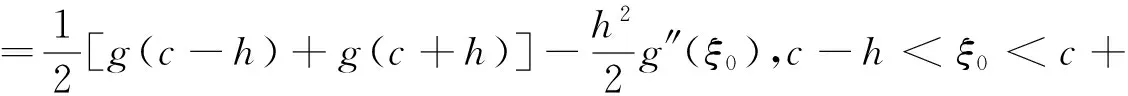
2 差分格式的建立
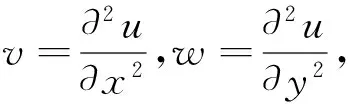

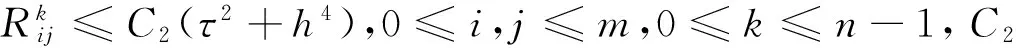
3 数值试验