基于网络图的大学生社团结构分析①
李双东 倪晋龙
(安徽大学江淮学院,安徽合肥230039)
基于网络图的大学生社团结构分析①
李双东 倪晋龙
(安徽大学江淮学院,安徽合肥230039)
大学生社团是校园文化的重要载体,既是提高大学生自身素质,开拓知识面,调整知识结构,发展个人兴趣、爱好和特长的有效途径,也是开展大学生思想政治工作的新的重要渠道.因此对大学生社团体系结构的分析和研究也越来越重要,这即是社团发展的内在需求,又是高校文化建设及和谐社会建设的外在要求.本文对安徽大学江淮学院社团的结构进行分析和研究,比较不同社团的模块度函数值分析社团专业性强弱,利用社团节点中心度分析不同专业学生在社团的中心地位,最后通过马尔科夫链模型预测各社团第二年的招新情况,这为研究评比社团提供标准以及为社团发展提供参考依据.
大学生社团,模块度函数,节点中心性,马尔科夫链
大学生社团是校园文化的重要载体,是建设思想政治教育和实施素质教育的重要途径和有效方式,在加强校园文化建设、提高学生综合素质、引导学生适应社会、促进学生成才就业等方面发挥着重要作用,是新形势下有效凝聚学生、开展思想政治教育的重要组织动员方式,是以班级、年级、系别为主开展学生思想政治教育的重要补充.积极活跃的高校社团活动可以调动学生兴趣爱好增强人际交往和动手能力,也对道德水平的提升起到潜移默化的作用.而优良合理的社团组成结构,可以提升社团的内涵以及深度,有利于社团活动的展开和社团的今后发展.因此一个好的高校社团能够在高校文化建设和思想政治教育两方面发挥更加重要的作用.随着我国大学社团的繁荣发展,出现了社团增多、跨社团跨校活动增多、与社会联系增多等新情况,同时也引发了许多新的问题,由此大学生社团的相关问题的分析和研究越来越受到众多学者、专家的关注.
通过大学生社团结构组成的分析和研究,能让我们正确的认识不同社团的结构特点,以及所表现出的社团专业性强弱和节点中心地位的差异,通过合理的马尔科夫链模型预测社团来年招新情况,为大学生社团的实践与运作提供参考依据,进而为构建和谐校园文化和谐社会服务.
1 社团结构的专业性
大学生社团的种类丰富多彩,大多数社团都是由不同专业的学生组成的,实际情况下,一些社团成员组成与专业的性质紧密相关.表1是安徽大学江淮学院的部分典型社团专业分布情况.
从表中数据可知,法学社和实践电子社中部分专业所占百分比很高且这些专业和社团性质紧密相关,而摄影社环境保护社和音乐声的专业分布比较平均,直观上得知法学社和实践电子社相比较与其他社团专业性比较强,除此之外并不能分析社团的其他结构特点.为研究此问题,利用matlab构造出了社团的网络结构图,如图1,图2所示.
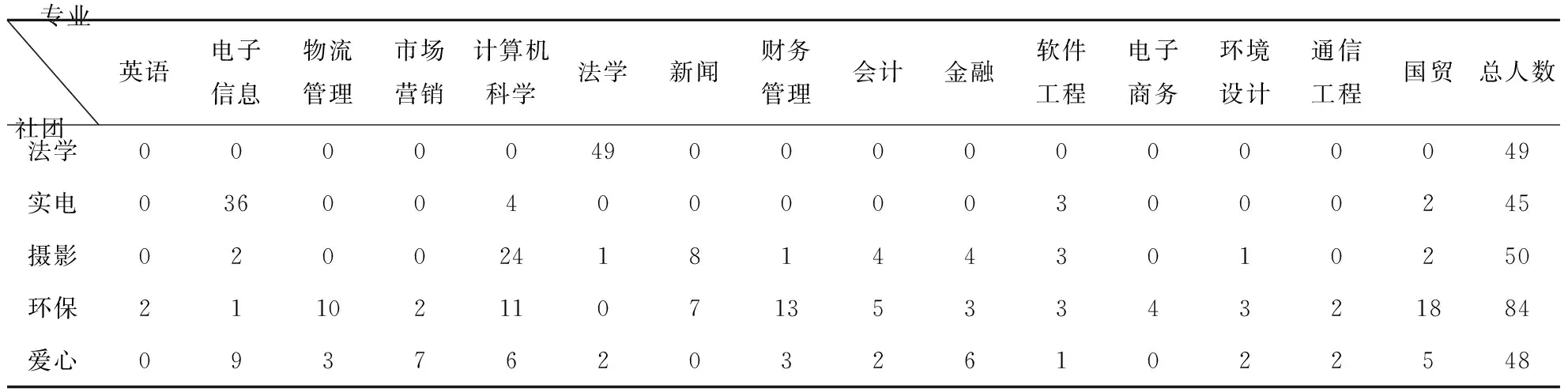
表1 安徽大学江淮学院2014年部分社团统计表

图1 实践电子社 图2 摄影社
说明:图中实线段中心连接点为社团的团长,分散的黑色点为社团成员,社团成员与社长之间用实线段连接,社团中同一个专业的成员间用线段连接.
分析上面两社团网络图:社团网络图中每个专业内之间的连接相对紧密,各个专业间的联系相对稀疏,结合社会学经典的“弱连接的强度”理论[1],从网络角度看,同一个专业的学生间大都数关系密切.因此弱连接对应于这些专业之间的稀疏的联系,强连接则是对于专业内部的紧密的联系,每一个专业内部的个体很有可能生活在相同或相似的圈子里,即他们接触和交流的多且主题相比较其他专业较为集中和相似.当社团中某些专业多占百分比较大,使得社团的交流更加活跃主题更加集中,那么这些社团的表现出的专业性会更加突出.因此,我们可以利用社团网络结构性来衡量不用社团的专业性强弱.在研究社团结构性过程中, Girvan和Newman定义的模块度指标Q用来定量地描述网络中的社团和刻画社团特性强弱[2],所谓的模块化是在网络中连接社团结构内部定点的边所占的比例与另外一个随机网络中连接社团结构内部顶点的边所占比例的期望值相减得到的差值.如果一个社团网络结果划分的好结构性强,则社团内部连接的稠密程度应高于随即连接网络的期望水平.其具体定义过程如下
假设网络已经被划分成社团结构,Ci是顶点i所属的社团(即本文中的专业),则网络中社团内部连边所比例可以表示成
(1)

实际应应用中,Q的最大值一般在0.3-0.7的范围内.计算时间法学社模块度指标值Q=0.019 2,电子社Q=0.330 4,爱心社Q=0.506 3,摄影社Q=0.566 6,环境保护社Q=0.641 62.数据表明社团专业性越弱的社团的模块度指标值越大,这表明专业性弱的社团组成分布更加分散,所以在网络图的社团结构划分中认为这种社团结构更加合理,越接近传统意义活动性社团.而专业性强的社团网络结构图更加紧凑,如法学社是全部由法学专业学生组成,其网络图是个完全图,所以此网络图模块度不高,但却能反映这个社团的专业性更强.因此社团网络图的模块度可以作为衡量社团专业性的强弱的一个指标.
3 社团节点的中心度
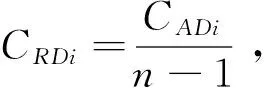
分析上表发现:(1)每个社团形成的网络中,均存在若干主节点次节点和边缘节点,各专业的中心性地位存在很大差异,电子信息专业和计算机科学专业的中心性地位最高,即在不同社团中的活动地位较高,活跃性比较强.(2)专业性十分强的社团吸引的专业数量比较少专业性质要求比较高,如法学社,而活动性和主题文化性比较突出的社团吸纳的专业数量比较多,专业性质要求比较低,如环境保护社和爱心社.(3)某些专业学生节点对其他专业的吸引度不同,同一学系下的专业间的集聚效果比不同学系的强,例如学校理工部下的电子信息专业、计算机科学专业和软件工程专业的在不同社团下的聚集现象比较相似.(4)个别专业在不同社团下均呈现为边缘节点,如软件工程和环境设计,说明这些专业学生在社团中的影响力和不强,这样不利于这些专业学生兴趣爱好的发展.
表2 各社团中专业学生节点相对中心值分类

图3 模块度指标分析结果
注:A为主节点,B为此节点,C为边缘节点.
4 社团网络的演化
大学生社团每年都有纳新活动,招新的人数和准备都是根据学校安排和以往经验计划的,又选取学院最新一年的社团数据,利用上面建立的模型分析不同社团的模块度指标.
分析结果如图3所示.我们发现通常情况下专业性强的社团,每年的社团模块度指标相对很稳定,而专业性差的社团,模块度指标波动很大,这就意味着常常出现部分社团招新人数过多过少,这将造成资源分配不合理.因此合理的数学模型预测第二年新生社团报名情况,根据模型的预测结果来计划第二年资源的分配是必不可少的.为解决此问题我们利用马尔科夫链模型[4],马尔科夫链模型是指:如果一个系统现在处于若干个状态中的某一个确定状态,进过一段时间开系统将会以某一个概率转移到另一个状态,这一转移概率仅依赖于现在的状态,与过去的历史无关.
一般,假设一个系统有n种可能状态,记作状态1,2,…,n.如果在某个观察期,该系统处于状态j(1≤j≤n),而在下一个观察期,他的状态转移到状态i(1≤j≤n)的概率为pij,则称pij为转移概率,pij(1≤i,j≤n)满足
0≤pij≤1,p1j+p2j+…+pnj=1.
(3)
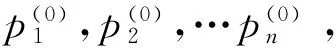
(4)
(5)
从而得到下一期系统处于状态i的概率,写成矩阵形式
(6)
一般的,如果矩阵P=(pij)的元素不随着时间变化,系统在第k期间的状态为P(k),则
(7)
因此,由初始状态可以预测系统在以后的个期间的状态,推广到大学生社团网络的演化.
假设一个学校里的有n个社团,每个社团的成员组成用一个n维的向量x表示为
(8)
其中,pi表示成员只参加了本社团的概率,pij表示成员参加i社团和第j社团的概率,于是可以刻画出不同社团间的向量构成的序列是一个马尔科夫链,对此取状态转移矩阵
(9)

图4 社团间成员组成矩阵图
第一列数值刻画的是第一个社团内部成员组成情况,只参加了第1个社团的学生概率为p1,参加了第1个社团和第2个社团的概率为p12,同理对p的其他列有类似的解释,图4给出这个矩阵的一个图表.
社团招新后,在各社团对所有成员做问卷调查,统计可以重新选择社团情况下他们想报名的社团,假如再一次调查统计中,结果为
(10)
pi是所有同学选择i社团的概率,所以第二年的社团发展情况可由x1描述,即
(11)
故第二年参加社团的同学中报名第1个社团的概率为p1,报名第2个社团的概率为p2,同理报名第n个社团的概率为pn.
通过模型分析我们可以预测到第二年新生社团报名情况,根据这些数据,我们可以合理安排招生计划,对于热门的社团我们控制好社团成员数量提高成员质量,冷门的社团要想办法吸引更多的学生报名发展社团.学院也可以干预引导,使得大学生社团结构总体更加合理
4 结语
大学生社团是大学生在校的一个重要活动中心,它可以培养大学生各方面能力,优秀的社团结构是学生学习成长的保证.本文利用MATLAB绘制出社团结构的网络图,通过社团结构的模块度函数,分析不同社团结构性强弱差异,进而反映社团的专业性.研究社团节点的中心性,得出不同社团中占中心地位的专业学生节点,并分析相关节点所表现的性质.利用马尔科夫链模型预测第二年招新情况,为社团的演化发展及社团建设提供参考.
[1]GranovetterM.Thestrengthofweakties[J].AmericanJournalofSociology,1973,78(6): 4360-1380.
[2] 李慧嘉.多尺度的社团结构分析方法研究[J].计算机学报,2014,10:68-110.
[3] 路紫.基于图论的SNS社区中人际节点空间关系的中心性研究——以新浪微博为例[J].经济地理,2013,12:78-81.
[4] 胡腾波,叶建栲.马尔科夫链模型在GIS数据预测中的引用[J].计算机系统应用,2008,33:10-30.
Analysis of College Students’ Association Structure Based on Network Graph
LI Shuang-dong NI Jin-long
(Jianghuai College,Anhui University,Hefei 230039,China)
College students’ community is an important carrier of campus culture, which is way to improve the quality of the students themselves, enlarge their knowledge, adjust the knowledge structure, develop personal interests, hobbies and expertise, and is also an important new channel to carry out ideological and political work. Therefore, it is more and more important to analyze and study the system structure of college students’ association, which is the inner demand of the development of the society,and the external requirement of the construction of university culture and harmonious society. In this paper we study college students’ community of Anhui University Jianghuai college. We ranked their professional attributes by comparing their values of modularity function,analysed the status of students from different majors in a community by the centrality degree index of community network. Finally we predict the situation of club in the next year through the Markov chain model .Our study will provide theoretical support to the rating standards for community and to the development for community.
college student association, modular function, node centrality, markov chain
2017-02-13
安徽省高等教育自然科学研究重点项目(KJ2016A044), 安徽大学江淮学院院级大学生创新实验计划(XC2016007)资助
李双东,lisd@ahu.edu.cn.
TP393
A
1672-6634(2017)02-0106-04

