直觉Fuzzifying 拓扑空间的子空间①

朱风梅 孟广武

(聊城大学数学科学学院，山东聊城252059)

直觉Fuzzifying 拓扑空间的子空间①

朱风梅 孟广武

(聊城大学数学科学学院，山东聊城252059)

直觉Fuzzifying拓扑是Fuzzifying拓扑的自然推广,是模糊拓扑学的重要分支.研究了直觉Fuzzifying拓扑的子空间理论,特别是内部算子和闭包算子理论.

直觉模糊集，直觉Fuzzifying拓扑，子空间

1 前言和预备知识

1983年，K. Atanassov[1].推广Zadeh的模糊集[2]引入了直觉模糊集的概念.直觉模糊集有更强的表达不确定性的能力，因而在诸多学科引起了广泛关注[3-8].直觉模糊拓扑[5]是直觉模糊集和拓扑学相结合的产物,它可以看作拓扑和模糊拓扑[9,10]的共同推广. 直觉Fuzzifying拓扑[11-14]是直觉模糊拓扑的重要分支.近年来,我们对直觉模糊拓扑进行了系列研究[11-13]:直觉Fuzzifying拓扑的邻域系、基和子基、Moore-Smith收敛理.另外,蒋沈庆[14]研究了Fuzzifying拓扑的分离性.

定义1[3]设X为非空集，称

2 直觉Fuzzifying拓扑的子空间

文献[1]给出了子空间的定义, 但并未给出证明,也未展开讨论.本文将较为细致的研究直觉Fuzzifying拓扑的子空间理论, 特别是研究其内部算子和闭包算子理论.

(1)

即

(2)对任意Vλ∈P(Y)(λ∈J)，

此时

从而得

(3)同(2)类似地，对任意V1,V2∈P(Y)，可证得

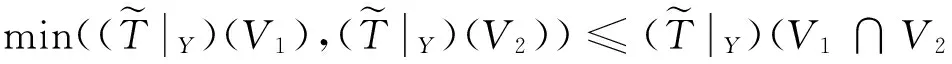
(W).

定理1 设Y是直觉Fuzzifying拓扑空间X的一个子空间,y∈Y.则

证明 (1)即是直觉Fuzzifying拓扑子空间和相对拓扑的定义.

3 结论

在已有工作的基础上,我们研究了直觉Fuzzifying拓扑的子空间理论. 在未来的工作中,我们将把这一理论应用于直觉Fuzzifying拓扑的连通性、紧性等拓扑性质的研究.

致谢 感谢聊城大学李令强老师的帮助，作者在阳谷县明德小学继续从事拓扑学研究.

[1]AtanassovK,StoevaS.Intuitionisticfuzzysets[J].ProcofPolishSymp.onIntervalandFuzzyMathematics,Poznan, 1983，8: 23-26.

[2]ZadehLA.Fuzzysets[J].InformandControl,1965, 8: 338-353.

[3]AtanassovK.IntuitionisticFuzzySetsTheoryandApplication[M].NewYork：Springer-Verlag,Heidelberg, 1999 .

[4] 徐小来,雷英杰,谭巧英.基于直觉模糊三角模的直觉模糊粗糙集[J]. 控制与决策, 2008, 8: 900-904.

[5]CokerD,DemirciM.AnintroductiontointuitionisticfuzzytopologicalspacesinSostak’ssense[J].Busefal, 1996, 67 : 67-76.

[6]CokerD.Anintroductiontointuitionisticfuzzytopologicalspaces[J].FuzzySetsandSystems,1997, 88: 81-89.

[7]AbbasSE.Intuitionisticsuprafuzzytopologicalspaces[J].Chaos,SolitonsandFractals,2004,21: 1 205-1 214.

[8] 毕文凤，朱风梅，李令强，等，直觉模糊拓扑空间的重域结构[J].山东理工大学学报：自然科学版,2010, 24(03): 14-16.

[9]HöhleU，RodabaughSE.MathematicsofFuzzySets,Logic,TopologyandMeasureTheory[M].KluwerAcademicPublishers,Boston, 1999.

[10]YingMingsheng.Anewapproachforfuzzytopology(I)[J].FuzzySetsandSystems, 1991, 39:303-321.

[11] 朱风梅,李令强,毕文凤,等. 直觉Fuzzifying拓扑的基和子基[J].鲁东大学学报：自然科学版，2011,27(1):13-15．

[12] 朱风梅,李令强,毕文凤,等.直觉Fuzzifying拓扑的Moore-Smith收敛理论[J].山东理工大学学报：自然科学版,2011,25(1):50-52．

[13] 朱风梅,孟广武. 直觉Fuzzifying拓扑:邻域系[J].商丘师范学院学报,2013,29(9):13-16.

[14] 蒋沈庆. 直觉不分明化拓扑空间的分离公理[J].鲁东大学学报：自然科学版,2014,30(3)：202-205.

Intuitionstic Fuzzifying Topology：Subspace

ZHU Feng-mei MENG Guang-wu

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059，China)

The notion of intuitionistic fuzzifying topology is a natural extension of fuzzifying topology, and it is also an improtant branches of fuzzy topologies. In this paper, we study the theory of subspace of intuitionistic fuzzifying topology, in particular, the theory of interior and closure operators.

intuitionistic fuzzy set，intuitionistic fuzzifying topology，subspace.

2017-01-09

国家自然科学基金资助项目(11501278)；聊城大学自然科学基金资助项目(318011505)资助

孟广武，E-mail:menggw@lcu.edu.cn.

O159.1

A

1672-6634(2017)02-0011-03