预应力简支桥梁基频简便计算方法

杨雷，黄从俊，方诗圣，卢建宇

（1.合肥工业大学土木与水利工程学院安徽合肥230009；2.合肥市规划设计研究院安徽合肥230041）

预应力简支桥梁基频简便计算方法

杨雷1，黄从俊2，方诗圣1，卢建宇1

（1.合肥工业大学土木与水利工程学院安徽合肥230009；2.合肥市规划设计研究院安徽合肥230041）

——以合肥地区为例

在实际的桥梁工程设计中，汽车荷载的作用取值为汽车荷载作用标准值乘以冲击系数，其中冲击系数是由桥梁的基频通过固定的公式计算而来。但目前，现有的规范中对于桥梁基频的计算公式复杂，因此结合合肥地区既有预应力简支梁桥，选取典型截面和跨径，采用Midas civi l建立有限元模型，计算出其一阶竖向振动频率，并利用MATLAB拟合出合理的快速计算简化公式，最后与JTG D60-2015规范中给出的计算公式作对比，通过实际案例来说明拟合公式的合理性与可行性。以期减少工程设计人员的计算负担，方便实际应用。

桥梁基频；简支；冲击系数；拟合公式

引言

随着十三五规划的开端，国家在新的5年计划中明确提出了构筑现代基础设施网络的要求，这也就意味着新一轮的公路桥梁基础建设将迎面而来。[1]在桥梁设计里，车辆荷载是影响设计活荷载取值的主要因素，而车辆荷载的冲击系数取决于桥梁自身的结构基频，桥梁工程师在面对繁杂的工程设计中，按照《公路桥涵设计通用规范》J T G D60-2015中规定的结构基频计算公式[2]计算，只因需要参数繁杂，计算起来尤为耗时，而规范中推荐的有限元计算方式，则更加耗时。因此迫切需要一种快速准确的计算方式。[3]为此在考虑到现有简支桥梁以预应力结构为主的情况下，本文将以合肥地区既有桥梁工程为例，选取典型跨径和断面，总结其中的规律，给出合理的拟合公式，以方便桥梁工程设计人员计算，减少工作量。

一、有限元模型计算

简支梁桥根据截面类型一般分为空心板梁和T型梁两种，在此分别讨论：

（一）空心板

选取桥梁工程实例参数：标准跨径：跨径20米；构件形式：现浇先张法预应力混凝土简支空心板梁；预制梁长：19.92m；计算跨境：18.92m；汽车荷载：公路-I级；结构重要性系数：1.1。

M i d as c i v i l有限元模型[4]信息：节点229个，单元298个；梁单元模型；各边梁均布荷载（二期恒载）取-21.6K N/m，各中梁均布荷载（二期恒载）取-11.9K N/m；自重系数z取-1.04（因为程序中的C50混凝土默认的容重?=25K N/m3，而C50混凝土的实际容重一般为26K N/m3，因为输入竖向系数26/25=1.04）；二期恒载包括桥面铺装C50混凝土、沥青混凝土和钢筋混凝土防撞强，均布荷载采用“梁单元荷载”定义。

结构基频求解设定：自重（将自重转化为z方向质量）+二期恒载（荷载转化为z方向质量）+预制横隔板（荷载转化为z方向质量）；特征值分析：采用L a n cz o s特征值向量分析法，取子空间迭代值计算第一振型频率为结构基频，[5]振型如图1所示。

图1 20m空心板一阶振型图（自重+二期恒载）

计算得到的基频f1=4.724666HZ（不考虑二期恒载）、f2=3.327952HZ（自重+二期恒载），同理16m、13m、10m跨径的空心板简支梁桥计算过程由于篇幅原因就不详细叙述，在此仅给出计算结果，如表1。

表1 空心板标准跨径有限元计算基频

（二）T型简支梁

选取桥梁工程实例参数：构件形式：装配式后张法预应力混凝土简支T形梁；标准跨径：30m；计算跨境：28.92m；斜交角度：30；汽车荷载：公路-Ⅰ级；结构重要性系数：1.1。

M i d as c i v i l有限元模型信息：节点125个，单元194个；材料定义为C50；荷载定义：自重系数z取-1.04；每片中梁承载的z方向荷载定义为qz=-11.9K N/m，每片边梁承载的z方向荷载定义为qz=-21.6K N/m，振型如图2所示。

图2 30mT型板一阶振型图（自重+二期恒载+横隔板）

计算结果显示基频f1=4.371946HZ（仅考虑自重）、f2=3.441140HZ（自重+二期恒载），同理20m、25m跨径的空心板简支梁桥计算过程由于篇幅原因就不详细叙述，在此仅给出计算结果，如表2。

表2 T型梁标准跨径有限元计算基频

二、合理拟合线性的选择

（一）合理线性的推测与计算

为了得到合理的拟合线形，选取空心板桥，在此观察以M i d as c i v i l计算基频（自重+二期）的数据作出的散点图[6]，横向X轴为跨径（m），纵向Y轴为基频（HZ），如图3所示：

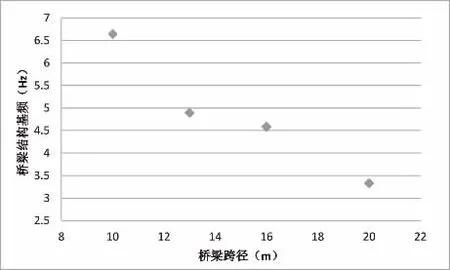
图3 空心板跨径与对应结构基频散点图

根据桥梁基频的散点图分布特征，笔者在此选取三种线形作为拟合备选方案：①方案一：y=a ebx+c；②方案二：y=a x2+bx+c；③方案三：y=kx+b，并根据拟合结果[7]择优选取最终拟合方程。

方案一、指数函数方程y=a ebx+c的形式

M A T LA B代码：

同理以方案一的原始拟合数据为蓝本，分别对方案二、方案三进行拟合，可得到一元二次方程y=0.0159x2-0.7878x+12.8104与一元一次方程y=-0.3093x+9.4259。

（二）最优线形的选取

根据拟合后的三个图形对应的方程，计算各个模型对应的误差平方和[8～10]Q=∑?〖(yi-yxi)2。

部分M A T LA B运行代码：

同理可以得到D2=0.4581、D3=0.3237。因为D2>D1>D2，所以可以得出结论：桥梁基频的拟合采用指数函数（y=a ebx+c）拟合效果最好，最终公式为y=15.4965e-0.1274x+2.2338。

三、拟合公式与规范计算数据对比分析

根据上一节分析得知，预应力简支桥梁的基频拟合公式采用指数函数形式为最佳，笔者以表1和表2的有限元软件计算数据，采用最小二乘法，分别对空心板、T型两种截面形式的预应力简支梁桥基频进行公式拟合，拟合曲线与原计算数据对比图如下图4所示。

图4 各类型、跨径预应力简直板桥拟合曲线与原数据对比图

建立各类型简支桥梁跨径L（m）与基频f（HZ）的函数关系：

（1）空心板桥

f=46.1693e-0.1846L+3.8398仅考虑自重

f=15.4965e-0.1274L+2.2338自重+二期恒载

（2）T型桥

f=31.3609e-0.0898L)+2.2516仅考虑自重

f=55.4220e-0.1240L+2.0980自重+二期恒载+横隔板

综上所述把所有的基频计算结果汇总与表3，以方便与规范计算结果作对比。

表3 各类型、跨径与规范、拟合公式的计算数据对比

由上表数据易看出，文中在仅考虑自重情况下给出的拟合公式计算基频与规范计算值相近，而考虑桥面铺装的计算值明显小于规范计算值，究其原因不难发现了，规范中计算结构基频仅仅考虑了跨中截面和材料特性值，并未考虑桥面铺装，所以规范给出的结算偏安全。反过来，在仅考虑自重情况下桥梁结构基频的计算值与规范相近，也印证了本文所建立的有限元模型是合理、可靠的。

四、具体案例验证

因为本文给出的公式是在标准跨径下拟合分析出来的经验公式，为了进一步说明本文所给出的简支桥梁结构基频计算公式应用的可靠性与广泛性，在此选用一个合肥地区现有的非标准跨径的简支梁桥进行验算。

合肥市西二环下穿黄山路桥是一个4跨空心板简支梁桥，材料为C50混凝土，桥跨分布为2 11m、2 15m，跨中截面信息手动计算结果为：（1）15m跨径，跨中截面惯性矩Ix=0.02896013m4、截面面积S=0.3812m2；（2）11m跨径，跨中截面惯性矩Ix=0. 02896013m4、截面面积S=0.3812m2，结构弹性模量E取3.45×1010N/m2，结构跨中每延米结构重力G取2.6×104N/m3，重力加速度g取9.806m/s2。

对于15m跨径的空心板，规范计算基频为f=6. 9376HZ，本文拟合公式（仅考虑自重）计算值为f=6. 7358HZ，相对偏差为2.91%；对于13m跨径的空心板，规范计算基频为f=9.6029HZ，本文拟合公式（仅考虑自重）计算值为f=9.8998HZ，相对偏差为2.97%。从非标准跨径的计算结果来看，本文给出的拟合公式可靠度高。

五、结论

（1）文中给出的仅考虑自重情况下桥梁结构基频计算公式，计算结果与规范计算值偏差度很小，桥梁设计人员仅仅需要根据桥梁类型和跨径，即可代替规范里面繁杂的基频计算，大大提高了工作效率。

（2）另外，文中除了给出了仅自重情况下的结构基频计算公式外，还给了考虑桥面铺装和护栏荷载情况下的桥梁基频计算公式，桥梁结构在实际运营过程中桥面铺装和护栏等荷载是包含在桥梁本身的质量里面的，这种情况下给出的计算公式与事实相符，但因计算值相对于规范来说偏小，所以这可以应用在桥梁结构设计的复核阶段，以供参考。

[1]新华网,十三五规划纲要,http：//www.sh.xinhuanet.com/ 2016-03/18/c_135200400_2.htm.

[2]中交公路规划设计院,JTGD60-2015,公路桥涵设计通用规范[S].北京：人民交通出版社,2015.

[3]杨旭.汽车荷载作用下梁桥的动力响应与冲击系数分析[D].重庆：重庆交通大学硕士论文,2016.

[4]邱顺冬.桥梁工程软件M idas civil应用工程实例[M].北京：人民交通出版社,2011.

[5]葛俊颖.桥梁工程软件M idas civil使用指南[M].北京：中国铁道出版社,2013.

[6]李斌.Excel2010应用大全[M].北京：机械工业出版社, 2010.

[7]陈超.MATLAB应用实例精讲——数学数值计算与统计分析篇[M].北京：电子工业出版社,2010.

[8]邓露,何维,王芳.不同截面类型简支梁桥动力冲击系数研究[J].振动与冲击,2015,34(14)：70-75.

[9]卜建清,娄国充,罗韶湘.汽车对桥梁冲击作用分析[J].振动与冲击,2007,26,(01)：52-55.

[10]刘琴.公路简支与连续桥梁冲击系数问题探讨[J].山西建筑,2015,41(21)：142-143.

U441

A

1671-5993（2017）02-0033-03

2017-03-28

安徽省住房和城乡建设厅科研开发项目（阶段性成果）；项目编号：2016YF-26

杨雷（1993-），男，安徽定远人，合肥市工业大学土木与水利工程学院硕士研究生，研究方向：道路与桥梁工程。