面积法在中学数学解题中的应用

安徽省合肥育英学校 赵 杰

面积法在中学数学解题中的应用

安徽省合肥育英学校 赵 杰

面积及面积法相关知识是中学数学学科教学中的重要内容之一，通过对面积和面积法的学习，一方面能够使学生更好、更直观地学习、理解和掌握数学知识，另一方面通过面积法构建“数形结合”几何模型，能够将中学数学中一些较为抽象和代数化的知识进行更为直观、具象的几何解释。这些都对培养学生的数学品质，理解数学思想，提升和强化学生的具象思维和直觉思维等大有裨益。

面积法；数形结合

一、面积法的定义

面积法是在面积理论基础上所推演出来的利用面积求解直接相关或间接相关数学问题的一种方法。关于面积法的定义，现行的教材上有明确的表述，即：采用某种特定的手段，使面积与面积、面积与边角关系等相互转化，从而使问题更加简单直观、易于解决的一种方法。在中学数学解题中，面积法是较为常见且运用频率较多的一种方法，其通常被运用于计算平面几何图形的面积问题，也常用于边角关系、线段的“和差倍分”关系等问题的证明。学生在解题过程中，若能灵活、熟练地使用面积法，将大大缩减解题步骤，降低问题难度，从而达到事半功倍的学习效果。

二、面积法在中学数学解题中的应用

在本章，笔者就简要介绍面积法在中学数学解题中的几种巧用。

1.用面积法证明线段间的关系

面积法的运用十分广泛，在证明线段的“和差倍分”关系时，面积法的作用和便捷性也不容忽视。通常情况下，证明平面图形线段的“和差倍分”关系大多需要添加一些辅助线，而采用面积法则大多数情况无需添作辅助线就可完成证明。即采用面积法求证线段间的关系，可以结合题目中已给出的条件来搭建图形面积间的关系，从而达到便捷解题的目的。与此同时，采用面积法求证线段的“和差倍分”关系还有助于开阔学生思路，启发学生思维，对学生综合素质的发展和提升十分有利。

例1 如图1所示，在△ABC中，CE为B边上的高，BD为AC边上的高，并且AB＞AC，求证：BD＞CE。

分析：本题求证线段BD与CE的大小关系，这属于线段“和差倍分”关系证明题中的一种。用面积法求证较为简单直观，可操作性很强。在证明过程中，教师可以将证明任务D＞CE转化为对△ABC的面积构建。

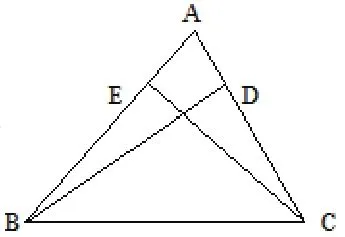
图1

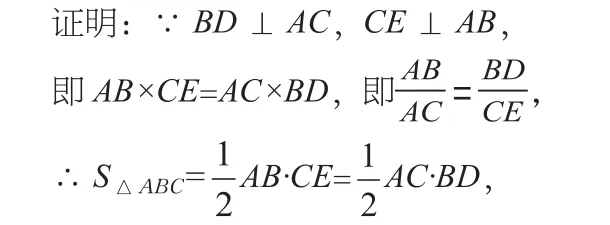
2.用面积法证明线段的比例等式

在证明线段的比例等式时面积法的作用也非常大，证明方法采用面积法，通过“面积”这一桥梁，巧妙地证明了几何图形中线段的比例关系，既直观又清晰，同时易于被学生所学习、理解和掌握。

例2如图2所示，已知△ABC中，E为AD的中点，连接BE，并延长交AC于点F，若BD∶CD=2∶1，求证AF∶FC=2∶3。

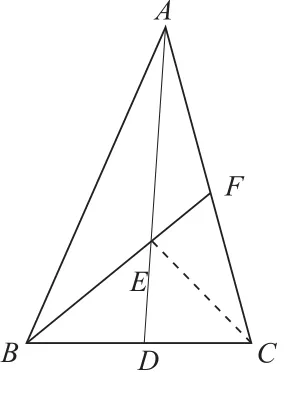
图2

3.用面积法得到一些有用的结论

（1）有一条公共边的两个三角形面积的比，等于它们的第三顶点连线被公共边分成的两条线段的比（内分比或外分比）。

（2）等边三角形内任一点到各边的距离的和是一个定值。

（3）梅涅劳斯Menelaus定理。

（4）（2）中推广到任意正n边形，其定值是边心距的n倍。

面积这块内容在中学数学教学中占据重要地位，其贯穿中学数学教学的始终。通过学习面积和面积法，并在数学解题中巧妙地运用面积法求解和证明问题，既可以帮助学生深刻理解“数形结合”的思想内涵，使其在解题过程中自觉树立起“数形结合”观念，建构出直观的几何模型和知识框架，进而掌握数学知识的本质内容，灵活运用、触类旁通，有力地打破传统中学数学教学中容易形成的思维定式弊端，又可以培养起学生的几何直观，化繁为简，化抽象为具象，解决以往学生普遍反映的畏惧平面几何这一问题，有助于增强学生自信，提高其数学素养和综合素质。

[1]黄启林.面积问题与面积方法[J].数学通讯，2011（09）.

[2]黄勇等.巧用面积法解几何题[J].语数外学习，2014（08）.