高中数学概念的教学不可弱化——以高中数学数列概念的教学为例

广东省广州市华侨中学 朱国璋

高中数学概念的教学不可弱化
——以高中数学数列概念的教学为例

广东省广州市华侨中学 朱国璋

数学概念是高中阶段数学教学的基础内容，现阶段，部分高中教师受到应试教育观念模式的限制，在开展数学教学的过程中，仅仅重视讲解习题，而忽略了对数学概念本身内涵的讲解，导致学生无法深入理解各种数学概念的内涵，基础不牢固，严重影响了高中学生数学基础知识的掌握。本文以数列概念的教学为例，对高中数学概念教学的重要性进行了说明。

高中数学；概念教学；难点；策略

一、高中数学概念教学

从当前高中数学概念课教学来看，教师常常在概念讲解的过程中，忽视概念教学的本质，由于学生只是被动接受概念的表面内容，导致很难实现真正意义上的数学构建。综合来看，当前的高中数学概念课教学中主要存在以下两个方面的问题：首先，教师由于受到应试教育体制的影响，在数学教学中往往更加重视培养学生的解题能力，忽视了对概念的深入解释；其次，教师在进行概念教学的过程中，直接要求学生对概念的解释内容进行死记硬背，无法让学生对概念的本质形成真正的认识和理解，导致学生无法将概念熟练地运用到实际习题中，产生反效果。

二、数列问题应对难点

以高中数学中的数列知识为例，虽然近年来高考数学考试大纲降低了对数列的考查要求，高考题的难度也有所下降，但是纵观近年来全国及各省市的高考数学命题情况，以等差数列和等比数列为主体的数列问题仍然给学生带来了一定的困惑。

（1）已知数列{an}的前n项之和的表达式为Sn=f（n），求{an}的通项an。

（2）对于“公比q含字母系数”的等比数列{an}，求其前n项之和Sn。

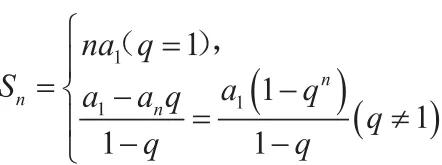
根据等差数列、等比数列在高考数学中的地位以及学生在面对这些题目时出现的问题，要养成滴水不漏、分类讨论的求解习惯。针对上面的两道例题，事实上，表达式中蕴含条件n＞1，而求和公式必须要满足q≠1的条件。因此，已知Sn求an时，或求等比数列的前n项之和时，必须进行分类讨论和求解。

下面以2015年高考数学湖南卷文科第19题为例进行分析：

设数列{an}的前n项之和为Sn，已知a1=1，a2=2，且an+2=3Sn-Sn+1+3，n∈N＊。

（1）证明：an+2=3an；

（2）求Sn。

该例题是一道包含数列证明和计算的综合性题目，给出Sn、an两者的递推关系，并对an+2、an的递推关系进行推演，然后求解Sn。该例题设计的主要目的是对学生思维的灵活性进行检测。

反思：在求证第一个问题的过程中，学生容易忽视验证“n=1”这一条件，导致丢失；在针对第二个问题时，巧妙地通过奇偶项求和方法，能够顺利进行求解。

三、高中数学概念教学策略

1.在概念教学中适当引入情境

部分数学概念与之前所学的概念存在一定的关联，教师可以利用之前已经讲授过的旧知识引入新的数学概念。比如等比数列概念的教学，其与学生之前所学的等差数列的概念存在一定的相关性。因此，教师在进行等比数列概念数学时，应该提前引入等差数列概念的复习内容，为学生创造一个熟悉的概念环境，然后给出数列，如：1,2,4,8,16…；1,3,9,27…等，让学生探寻其规律，学生能够更加容易地试探每两个前后数之间的差、和、积、商是否存在关联，进而探寻出数列的等比特征，同时在等差数列概念的基础上自己总结出等比数列的概念。

2.注重概念的内涵和外延

数学概念包含内涵和外延两个部分，其中内涵主要是对数学对象本质特征的体现，外延则体现了数学对象全体，将数学概念的内涵及外延充分揭示出来，能够使学生对数学概念形成更加深入的理解。数学概念的学习和理解需要循序渐进，因此教师在进行数学概念讲解的过程中，需要引导学生不断地自我思考和总结，从而不断完善对概念本质的认知。

3.注重抽象概念的直观表达

高中数学概念本身具有极强的抽象性，学生对其认知难度非常大，教师在对这些概念进行教学的过程中，应该借助图形、事物模型等实际例子，或者通过多媒体工具，将概念的本质更加直观地展示给学生，从而提升学生对数学概念的理解和认知。

当前，高中数学轻概念、重应用的教学现象普遍存在。在高考中，很少会直接考查察数学概念的具体内容，而是将其融入应用中。教师首先需要对数学概念有着非常深刻的认识和理解，才能更好地使学生掌握数学概念，同时还应该根据实际情况创设合理的教学情境，引入数学概念，并加强概念的内涵和外延以及对抽象概念的直观表达，使学生能够更加深刻地理解到数学概念的本质含义，更好地应用和扩展。

[1]姜艳辉.高中数学概念课教学初探[J].延边教育学院学报，2013（05）：105-108+112.

[2]苏振新.高中数学概念的教学方法研究[J].黑河学刊，2014（12）：95-96.