基于主成分分析和粒子群优化支持向量机的边坡稳定性评价

王晨晖

（河北地质大学勘查技术与工程学院，河北石家庄 050031）

基于主成分分析和粒子群优化支持向量机的边坡稳定性评价

王晨晖

（河北地质大学勘查技术与工程学院，河北石家庄 050031）

为科学评价边坡工程的稳定性，优化边坡稳定性的预测精度，提高工作效率，提出了基于主成分分析法（PCA）和粒子群算法（PSO）优化的支持向量机（SVM）模型。首先利用主成分分析法对边坡稳定性影响因子进行特征提取，以获得的主成分作为支持向量机的特征向量建立支持向量机模型，然后通过粒子群算法优化支持向量机参数，最终建立边坡稳定性评价模型，并对边坡实例的稳定性进行预测，结果表明：PCA-PSOSVM模型的运行速度快，预测准确率达90.9%，满足工程要求。

边坡；稳定性；主成分分析法；粒子群算法；支持向量机

0 引言

边坡稳定性评价一直是路基工程设计与施工的关键和难点，其稳定性是由多个影响因素共同作用的结果［1，2］。传统的定量分析方法忽略了模型建立的客观性，参数的选择也缺少必要的依据，导致预测准确率较低［3－5］。近年来，许多专家学者开始运用模糊理论［6］、灰色系统［7］和神经网络［8］等方法来实现边坡稳定性的预测，以上研究均取得了一定的成果，但是也存在模糊理论隶属函数的主观性、神经网络的收敛较慢等问题。

支持向量机作为一种新型机器学习方法，它继承了统计学习理论的关键思想，能够利用有限的样本数据建立准确的预测模型，具有良好的推广性能［9］。罗战友［12］和徐飞［13］的研究都表明，支持向量机方法在边坡稳定性评价中的科学性和有效性。但对支持向量机的参数优化问题一直没有较好的解决方案。粒子群优化算法是模拟群体智能的、启发式随机的优化算法，有较强的全局优化特性和全局搜索能力，谷文成［14］和高昆仑［15］等均用PSO优化选择最佳的支持向量机参数。此外，边坡稳定性影响因子间的冗余信息增加了模型的计算量，而主成分分析法能够提取影响因子的主要信息，降低计算复杂度。

基于此，本文建立了基于主成分分析法的粒子群算法优化支持向量机模型，试图为边坡稳定性评价提供一个新的方向。

1 基本原理

1.1 主成分分析法

主成分分析法是通过构造原变量的线性组合来得到维数较少且互不相关的新变量，这些新变量能够反映原始变量所提供的大部分信息，通过分析新变量来解决实际问题。其具体实现步骤为：设（X1，X2…Xn）是总体X的n个样本，每个样本观察m维变量，观测数据矩阵可记为：

首先计算该矩阵的协方差阵，为了避免不同变量间量纲差异导致的总体方差受较大方差变量控制的问题，根据公式将协方差阵化为其对应的相关系数阵。然后求出相关系数阵的特征值λ1≥λ2≥…λm≥0，计算得到它们对应的正交单位化特征向量e1，e2，…em。第i个主成分的贡献率为λi／P，其中i＝前q个主成分的累计贡献率为对比总结前人经验［16］，当前q个主成分累计贡献率达85%以上时，用这q个主成分来代替初始的影响因素进行分析一般是满足工程要求的。

1.2 粒子群优化算法

粒子群优化算法是模拟群体智能的、启发式随机的优化算法，有较强的全局优化特性和全局搜索能力，算法流程图如图1所示。

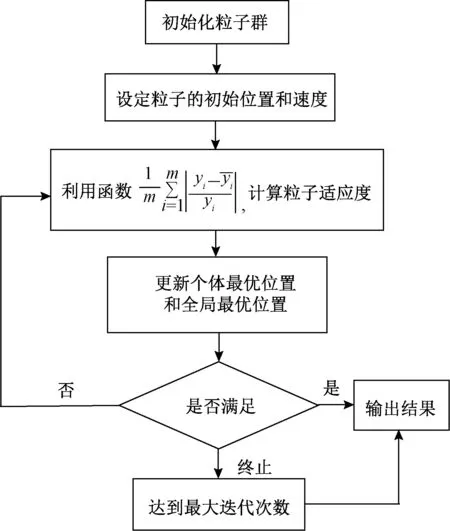
图1 粒子群算法流程图Fig.1 The flow chart of PSO

1.3 支持向量机

支持向量机（SVM）是由Vapnik［16］于1995年根据统计学习理论提出的一种在有限样本下进行机器学习的方法，其原理如下：

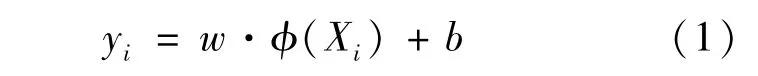
其中：w称为可调的权值向量，b为偏置值，且w和φ（Xi）均为n维向量。寻找最优的分类超平面亦即寻找最优的w和b。由于拟合误差的存在，引入ξ和ξ∗作为松弛变量，采用ε－SVR模型建立带有约束条件的模型优化函数：

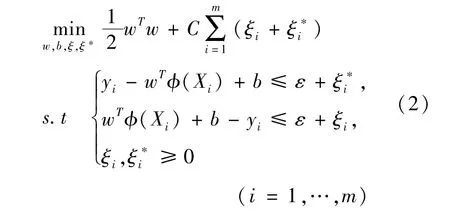
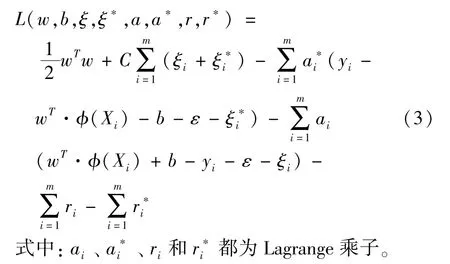
（3）式分别对w和b求偏导并置零，反代回（3）式中就可以得到上述问题的对偶问题，找到对应的KKT条件，并使用二次规划优化算法（Sequential Minimal Optimization，SMO）作为训练算法依次计算得到参数ai和对应的最优乘子同时构造得到预测函数：

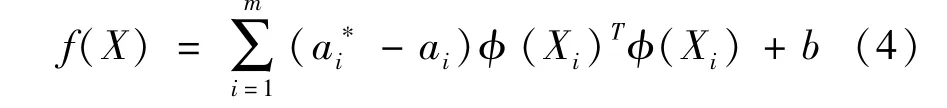
非线性映射ϕ的表达式很难确定，故引入核函数（Kernel）将原始特征的内积平方和等价为映射后的特征内积平方和，从而间接的求解非线性映射φ。满足泛函Mercer定理的核函数均可作为有效核函数，其中径向基核函数RBF具有较宽的收敛域，为解决实际问题中最常用的核函数。

2 边坡稳定性评价

通过总结分析前人经验，采用文献［18］中的41个边坡工程实例进行学习和预测。随机选择30个边坡用于训练支持向量机模型，剩余11个边坡作为预测样本。输出为边坡稳定性，边坡稳定性分为两类分别是破坏与稳定。其中破坏边坡的稳定性对应数值为－1，稳定边坡的稳定性对应数值为＋1。

利用PCA对6个边坡稳定性影响因子进行分析，相关系数矩阵如表1所示，由表1可以看出，重度与内聚力、摩擦角有较大的相关性，三者都是描述岩土体性质的参量；边坡角与边坡高之间存在一定的相关性，两者均是表征边坡尺寸和坡形的参数。若盲目选用以上相关性指标进行分析，会导致模型失真或难以准确判断。因此有必要利用主成分分析法构造新的主成分，降低模型复杂度［19］。

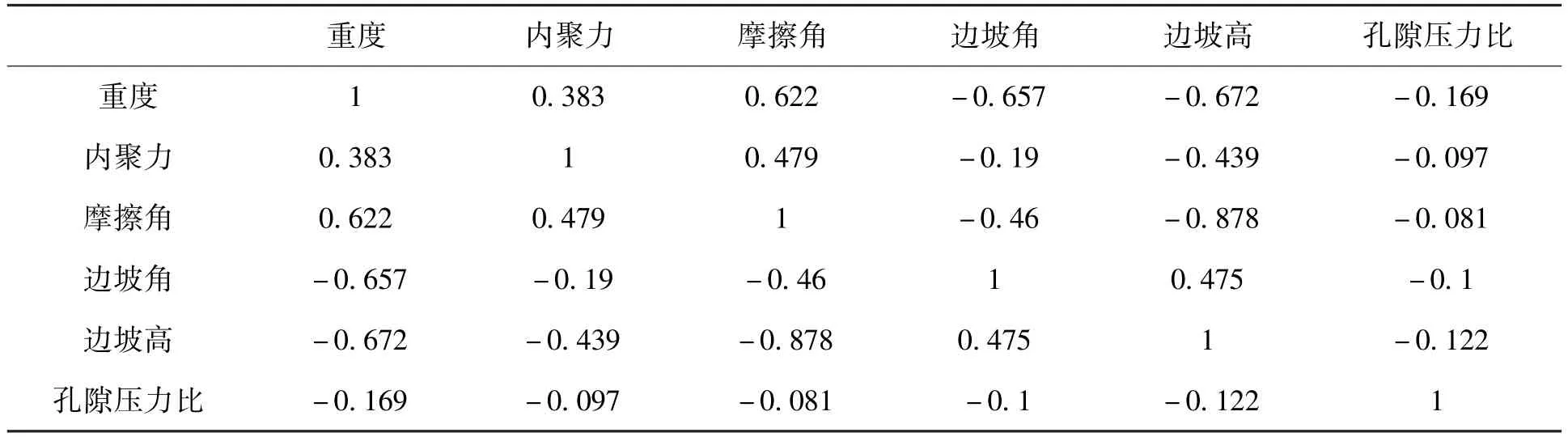
表1 相关系数阵Tab.1 Correlation coefficient matrix

通过以上分析得到的归一化特征值，各成分贡献率和累计贡献率如表2所示。

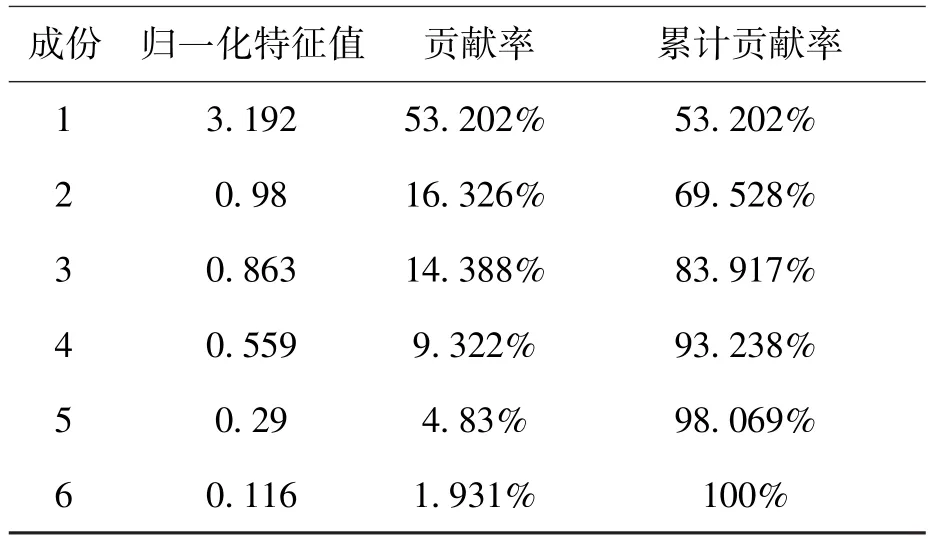
表2 归一化特征值、贡献率和累计贡献率Tab.2 Normalized eigenvalue，contribution rate and cumulative contribution rate

从表2中可以看出，前4个主成分的累计贡献率为93.238%，基本能够反映原来6个变量所携带的信息，这4个主成分的表达式见式（4）。将提取出的4个线性无关的主成分代替原来的6个影响因素作为输入变量来建立支持向量机模型，有效降低了变量的维数，提高了模型的运算效率。

3 模型建立

本文选择径向基函数（RBF）作为SVM分类的核函数，其性能取决于核参数g和惩罚参数C。为此，采用MATLAB语言编写PSO优化SVM模型参数程序，以表中的4个主成分作为输入变量，采用粒子群算法确定SVM的参数C和g，粒子个数n＝20，种群维数M＝100，最大迭代次数为200，加速度常数c1＝c2＝2，惯性权重取0.5。经过多次训练，确定SVM的最优惩罚参数为C＝ 4.7692，g＝1.4134。利用参数c和g确定的PSOSVM模型对学习样本进行训练和回判，结果如图2所示。

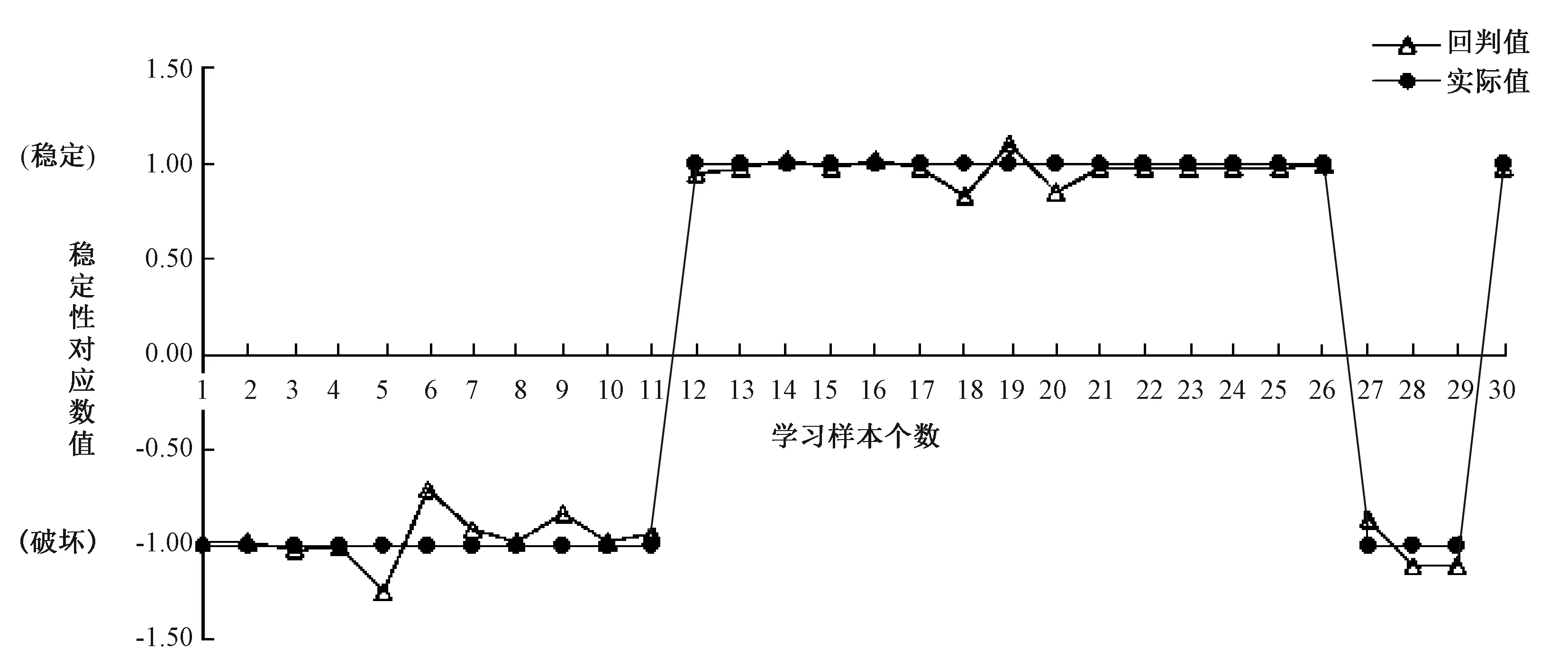
图2 学习样本回判结果Fig.2 The return result of study samples

由图2可以看出，回判曲线与实际曲线基本吻合，模型对学习样本有良好的回判效果，其中最小绝对误差为0.003，最大绝对误差为0.3，相对误差分别为为0.3%和30%，表明PCA-PSO-SVM模型满足工程要求的精度，可以预测边坡的稳定性。

将建立的PCA-PSO-SVM模型用于预测样本，考虑到网格搜索法（Grid Search Method，GSM）和遗传算法（Genetic Algorithm，GA）也具备优化参数的能力，故将其引入得到不同模型的预测结果，如表3所示。

表3 不同模型的边坡稳定性预测Tab.3 Slope Stability Prediction Based on Different Models

由表3可以看出，在三种参数优化方法中，粒子群算法优化的支持向量机模型拥有更高的准确率，表明粒子群算法优化支持向量机参数的能力是优于另外两种寻优方法的。同时，粒子群优化支持向量机模型的运行时间较少，肯定了粒子群算法在收敛速度方面的高效性。此外，无论是将原始数据，还是将提取的主成分作为模型输入，支持向量机的边坡稳定性评价模型均有着很高的准确率，再次证明了支持向量机在边坡稳定性评价中的可行性。同时也可以看到，在运用主成分分析法降低样本维度缩短运行时间的情况下，模型的预测精度并未受到影响。

4 结论

本研究根据边坡稳定性与影响因子间复杂的响应关系建立了基于主成分分析方法的粒子群算法优化支持向量机模型。将该模型用于样本预测，得出如下结论：

（1）主成分分析法采用降维的思想，确定的4个主成分表达了6个变量所携带的信息量的93.238%，剔除了变量之间的冗余成分，提高了模型的运行效率。

（2）PSO优化算法具有简便、快捷且高效的特点，优化了支持向量机的参数，将PCA-PSO-SVM用于预测11个边坡样本，预测准确率达90.9%，能够符合工程要求。

［1］ 赵建军，贺宇航，黄润秋，等.基于因子分析法的边坡稳定性评价指标权重［J］.西南交通大学学报，2015，40（2）：325－330.

［2］ 陈国庆，黄润秋，石豫川，等.基于动态和整体强度折减法的边坡稳定性分析［J］.岩石力学与工程学报，2014，36（2）：243－256.

［3］ 袁颖，王帅伟，刘珊珊.落石落距的影响因素敏感性分析［J］.防灾科技学院学报，2015，17（4）：49－55.

［4］ 秋实，左三胜.某边坡地震工况下的稳定性数值模拟分析［J］.防灾科技学院学报，2015，17（1）：47－52.

［5］ 史秀志，周健，郑纬，等.边坡稳定性预测的Bayes判别分析方法及应用［J］.四川大学学报（工程科学版），2010，35（3）：63－68.

［6］ 王艳霞.模糊数学在边坡稳定分析中的应用［J］.岩土力学，2010，30（9）：3000－3004.

［7］ 张正虎，袁孟科，邓建辉，等.基于改进灰色－时序分析时变模型的边坡位移预测［J］.岩石力学与工程学报，2014，（S2）：3791－3797.

［8］ 李元松，陈文峰，李新平，等.基于模糊神经网络的边坡稳定性评价方法［J］.武汉理工大学学报，2013，26（1）：113－118.

［9］ 饶运章，黄永刚，张永胜.支持向量机在边坡稳定性预测中的应用［J］.工业安全与环保，2016，28（7）：37－39＋54.

［10］ 胡军，王凯凯，董建华.基于BCABC-SVM的边坡稳定性预测［J］.沈阳工业大学学报，2016，25（2）：222－227.

［11］ 俞俊平，陈志坚，武立军，等.基于蚁群算法优化支持向量机的边坡位移预测［J］.长江科学院院报，2015，19（4）：22－27.

［12］ 罗战友，杨晓军，龚晓南.基于支持向量机的边坡稳定性预测模型［J］.岩石力学与工程学报，2005，30（1）：144－148.

［13］ 徐飞，徐卫亚，王珂.基于蚁群优化最小二乘支持向量机模型的边坡稳定性分析［J］.工程地质学报，2009，28（2）：253－257.

［14］ 谷文成，柴宝仁，滕艳平.基于粒子群优化算法的支持向量机研究［J］.北京理工大学学报，2014，36（7）：705－709.

［15］ 高昆仑，刘建明，徐茹枝，等.基于支持向量机和粒子群算法的信息网络安全态势复合预测模型［J］.电网技术，2011，20（4）：176－182.

［16］ 齐敏芳，付忠广，景源，等.基于信息熵与主成分分析的火电机组综合评价方法［J］.中国电机工程学报，2013，33（2）：58－64.

［17］ Vapnik V N.1995.The nature of statistical learning theory［M］.New York：Springer-Verlag：23－105.

［18］ 高国朋，颜可珍.基于距离判别分析法的边坡稳定性预测模型及应用［J］.水利与建筑工程学报，2010，24（3）：43－45.

［19］ 周爱红，尹超，袁颖.基于主成分分析和支持向量机的砂土渗透系数预测模型［J］.云南大学学报自然科学版，2016，38（5）：742－749.

Slope Stability Assessment Based on Principal Component Analysis and Support Vector Machine Optimized by Particle Swarm Optimization

Wang Chenhui
（School of Prospecting Technology＆Engineering，Hebei GEO University，Shijiazhuang 050031，China）

To ensure a scientific evaluation for stability of slope engineering，optimization of the prediction accuracy of slope stability，and enhancement of efficiency，the support vector machine（SVM）model optimized by particle swarm optimization（PSO）was proposed.First，PCA was used to extract main features from influential factors of slope stability，the acquired principal components were taken as the eigenvectors of SVM to build SVM model，and then PSO was adopted to optimize SVM parameters.Finally，the assessment model of slope stability was established and used to predict the stability of slope examples.The results show that PCA－PSO－SVM model features speediness in running，a high prediction accuracy of 90.9%，fully meeting the general engineering requirements.

slope；stability；principal component analysis；particle swarm optimization；support vector machine

TU457

：A

：1673－8047（2017）02－0026－06

2017－02－28

国家自然科学基金项目（41301015）；河北省教育厅重点项目（ZD2015073、ZD2016038）；石家庄经济学院国家自然科学基金预研基金（syy201308）；河北地质大学第十三届学生科技基金重点科研项目（KAG201607）

王晨晖（1992—），男，硕士研究生，主要研究方向为地质灾害治理与防治。