考虑屈曲行为的钢筋力学性能数值仿真分析

曹艳辉，贾俊峰

（北京工业大学建筑工程学院，北京 100124）

考虑屈曲行为的钢筋力学性能数值仿真分析

曹艳辉，贾俊峰

（北京工业大学建筑工程学院，北京 100124）

为评估考虑结构中纵筋受压屈曲形态的力学性能，采用ABAQUS有限元软件对长径比（L／D）不同的纵向钢筋在轴向压缩和循环荷载下强度和刚度的变化情况进行数值仿真，同时考虑加载历史和加载方式对钢筋力学性能的影响。结果表明，屈曲对纵向钢筋力学性能影响比较显著，纵向钢筋压缩性能取决于L／D，与钢筋屈服强度无关；钢筋在循环荷载作用下其力学性能受到加载历史、塑性变形、累积损伤以及L／D的影响，拉伸超过屈服应变后将导致钢筋压缩强度的损失，塑性变形和循环加载共同导致了钢筋累积损伤，钢筋屈曲行为造成了受压时钢筋强度和刚度的退化，并且随着L／D的增加钢筋强度和刚度退化越显著。

钢筋屈曲；长径比；压缩性能；循环性能；数值仿真

0 引言

纵筋的压缩以及循环性能对于评估现代钢筋混凝土（RC）建筑结构具有重要意义。对于仅承重结构，如果未严格按照设计规范的要求造成箍筋间距过大，并且钢筋混凝土柱承受较大轴压时，会大大提高结构中纵筋受压屈曲的可能性。除此之外，一些老旧建筑中由于混凝土的开裂和钢筋的锈蚀，箍筋对纵筋的约束作用减小造成纵筋屈曲问题更加严重。尤其在地震力作用下，纵筋循环压应力效应会加重纵筋屈曲反应，极易造成结构的承载力突然丧失。纵筋屈曲的现象常发生在梁柱节点和钢筋混凝土柱塑性铰区。图1为钢筋混凝土梁柱节点塑性铰区由于箍筋间距过大造成纵筋屈曲。钢筋在压缩和循环荷载下不同L／D（其中，D为钢筋直径，L为是箍筋间距）时其力学响应明显不同，原因是屈曲的发生会造成荷载响应下刚度和强度发生明显变化。因此评估现有建筑的抗震性能，钢筋的压缩以及循环特性至关重要。

图1 节点箍筋间距过大时纵筋屈曲现象Fig.1 Phenomenon of buckling of longitudinal bars in joints when the stirrup spacing is too long

为考虑RC结构中纵筋屈曲现象，国内外很多学者采用试验和仿真的方法研究了单筋的力学性能。为提出钢筋屈曲本构模型，通常的做法是将钢筋受压屈曲的“结构”力学性能等效为材料的应力－应变关系。1992年，Monti-Nuti［1］在钢筋试验的基础上，研究了屈曲对钢筋的单调以及循环性能的影响，结果显示，屈曲发生在L／D大于5时，屈曲导致了压缩时出现屈服后软化段，实验建立了考虑非弹性屈曲的分析模型，适用于分析钢筋混凝土离散纤维模型。1997年，Gomes-Appleton模型［2］修正了Menegotto-Pinto循环应力－应变钢筋本构，考虑了纵筋受压屈曲的影响，屈曲应力－应变关系通过屈曲后钢筋的塑性机理平衡方程来考虑。2002年，Dhakal-Maekawa［3，4］模型通过有限元模拟钢筋的失稳机制，认为钢筋屈曲的应力－应变关系可以用钢筋屈服强度的平方根和L／D来表示，通过修正Giuffre-Menegotto-Pinto模型提出并验证了考虑屈曲的钢筋应力－应变本构关系。2009年，Kunnath等［5］将Gomes-Appleton［2］和Dhakal-Meakawa［3－4］提出的可考虑钢筋屈曲的本构模型引入到OPENSEES中开发出Reinforcing Steel材料模型用于考虑钢筋的屈曲。2015年，杨红等［6］针对Reinforcing Steel中的Gomes-Appleton［2］模型引入OPENSEES时所采用修正方法存在的缺陷进行了修正，开发出修正后的Reinforcing Steel模型，能够更好地模拟试验钢筋的屈曲受力特征。2016年，方自虎等［7］将Vecchio的单调荷载三折线应力－应变曲线修正为二折线，提出了循环荷载下考虑钢筋屈曲影响的应力－应变关系模型，并在有限元软件ABAQUS中对该材料模型进行二次开发，所提出的模型可较合理地预测钢筋屈曲和未屈曲时钢筋混凝土结构的循环性能。除此之外，为考虑既有建筑中钢筋锈蚀的影响，一些学者也开展了锈蚀钢筋屈曲本构方面的研究［8－10］。现有研究普遍认为钢筋在L／D大于5时可能发生屈曲，钢筋的力学性能与L／D有关，但其针对的都是L／D较小的情况。

为考虑RC结构中纵筋屈曲长度，通常认为RC结构中钢筋屈曲的长度等于箍筋间距（局部屈曲），但试验中发现屈曲长度可能等于几倍的箍筋间距（全局屈曲）［11］。Dhakal和Maekawa［12］采用能量法计算得出矩形RC柱中不同屈曲模态所需要的箍筋刚度，并与决定钢筋稳定屈曲模态的实际箍筋刚度进行了比较，通过大量试验数据对比验证了屈曲长度计算方法，有助于在研究箍筋与纵筋共同作用时的RC结构抗震性能，对于考虑箍筋影响的纵筋本构关系也有指导性意义。此外，Kashani等［13］基于Dhakal和Maekawa［12］的方法提出圆形RC柱的屈曲长度计算方法。

为考虑纵筋屈曲下钢筋混凝土柱（墩）力学性能的仿真模拟，Zong和Kunnath［14］等采用了实体单元进行建模，期望得到简单可靠的考虑RC柱中纵筋屈曲的钢筋本构，对不同纵筋和箍筋的全尺模型进行了仿真分析，得到纵筋屈曲发生的机理。现在普遍接受的模拟考虑纵筋屈曲下钢筋混凝土柱（墩）的方法是采用纤维单元加考虑屈曲的钢筋本构模型建模［13，15，16］，模拟结果与试验结果较一致，能够很好地模拟RC柱的滞回性能。

为分析现有建筑结构的所有不同情形，本文考虑钢筋屈曲行为，进行大量的钢筋压缩及循环性能数值仿真分析，旨在评估钢筋L／D的临界值以及循环荷载下不同L／D钢筋强度和刚度的变化特征。

1 轴向压缩荷载下钢筋力学性能

为研究钢筋在压缩状态下的力学性能，采用Cosenza［17］材料拉伸试验的数据，如表1所示。首先验证模拟方法的正确性，图2a为模型最终变形结果。图2b为钢筋圧缩曲线对比，结果显示，ABAQUS有限元软件可较好地模拟钢筋受压时的屈曲行为和压缩力学性能。如无特殊说明后续轴向压缩模拟时材料参数均采用Cosenza钢筋拉伸试验的数据。

表1 钢筋拉伸试验参数［17］Tab.1 Tensile property parameters of tested bars［17］

1.1 屈服强度对钢筋压缩性能的影响

图2 模型变形及结果对比Fig.2 Model deformations and their comparison results

图3给出了三种不同屈服强度L／D＝10的压缩曲线，选用三种不同屈服强度的理想弹塑性本构（300～500MPa为现有常用钢筋屈服强度），弹性模量设为200GPa，对L／D＝10的钢筋进行了轴压荷载仿真。结果显示，三种强度不同但L／D相同的钢筋，其压缩曲线差别很小，可认为钢筋单轴压缩性能与钢筋屈服强度无关。该结论好像与Meakawa［3－4］等研究结论不一致，其认为钢筋归一化应力－应变曲线可通过表达，因此本文进行了三种特殊屈服强度和L／D工况下的模拟分析（都约等于200），如图4所示，结果显示三种工况下对屈服应变εy归一化时曲线相同，与本文研究结果并不相悖。

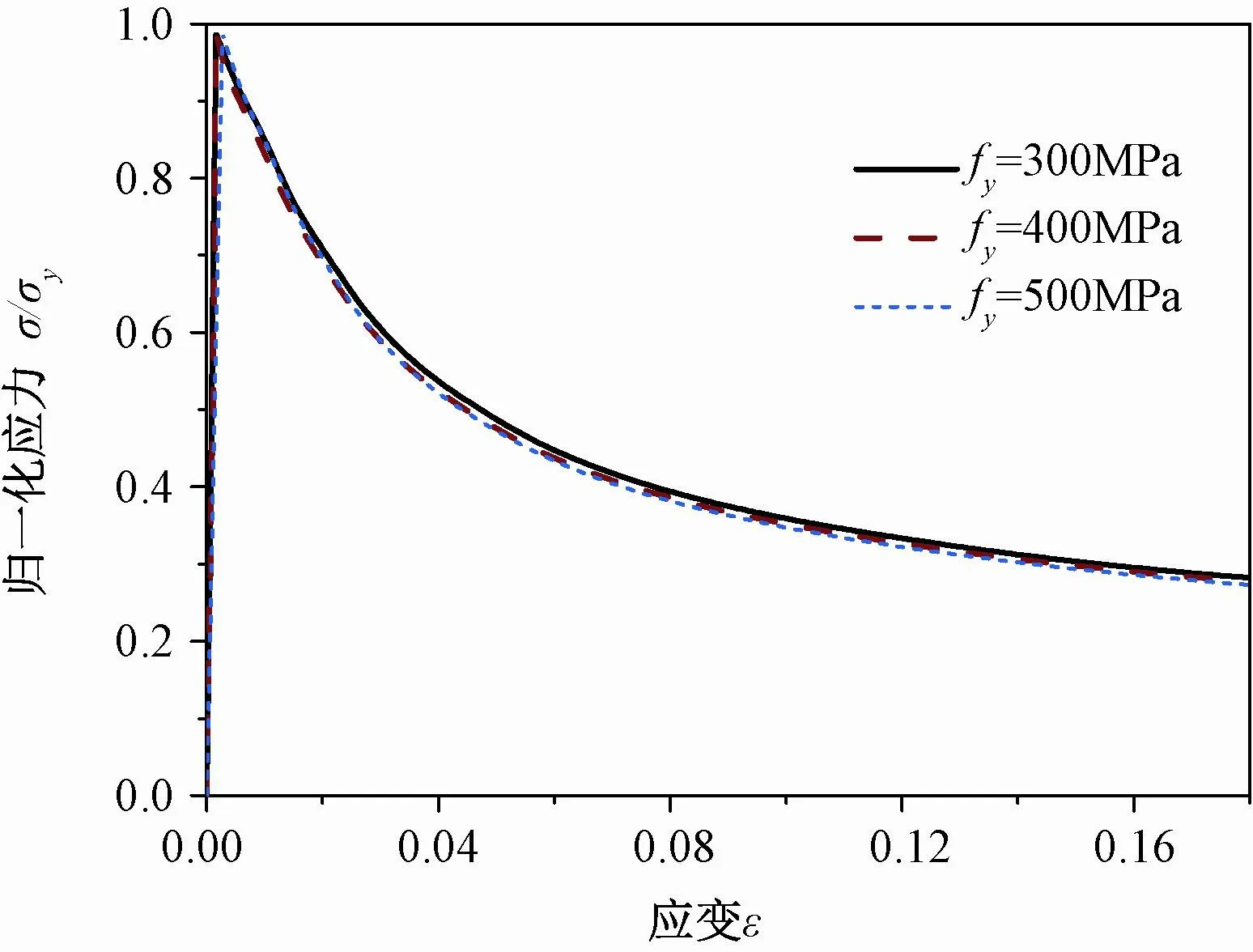
图3 L／D＝10时屈服强度不同的压缩曲线Fig.3 Compressive curves for different yield strengths when L／D＝10

1.2 直径对钢筋压缩性能的影响

图5给出了L／D为8的钢筋在四种不同直径时的压缩曲线，模拟结果说明钢筋的压缩性能仅受L／D影响，而与钢筋的直径没有关系。以上研究结果可以说明影响钢筋压缩性能的唯一影响因素是L／D。为研究不同L／D下钢筋的压缩性能，后续内容均采用直径为12mm的钢筋建模。

图4 应变归一化的压缩曲线Fig.4 Compressive curves of normalized strain

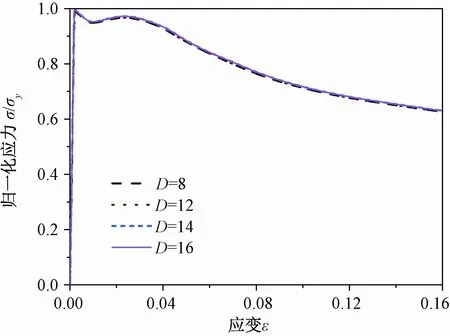
图5 L／D＝8直径不同的钢筋压缩曲线Fig.5 Compressive curves for different diameters when L／D＝8

1.3 L／D对钢筋压缩性能的影响

图6给出了5≤L／D≤20时钢筋的压缩曲线以及钢筋材性拉伸时的曲线，模拟曲线可以反映出如下特征：

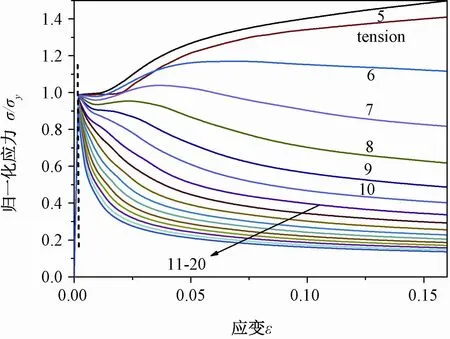
图6 不同L／D钢筋压缩曲线Fig.6 Compressive curves for different L／D

（1）L／D＝5时压缩曲线与材性拉伸曲线非常接近，可以认为L／D＝5时压缩和拉伸性能相同。

（2）L／D＜8时钢筋在屈曲前将发生一定程度的强化，对于L／D＝6和7分别在0.18及0.05应变之前保持大于屈服应力的强度，说明钢筋此时延性较好。

（3）8≤L／D≤20时钢筋将在屈服点附近发生屈曲，且不会发生强化现象，对于L／D＝20时其屈服点约为0．95σy，并且屈服点处下降段的切线大致为一条竖直线，可认为L／D＞20以后钢筋在受压时发生弹性屈曲。

2 循环荷载下钢筋力学性能

在钢筋受压数值仿真分析基础上，由于普通一维应力－应变本构并不能准确模拟钢材循环荷载作用下的性能，Chaboche钢材塑性本构模型［18］采用von Mises流动法则，其包含各向同性硬化和随动硬化两部分，能更好地模拟钢材在循环荷载下的力学性能。本文采用与Prota［19］试验中钢筋屈服强度近似的Q345钢材混合硬化参数模拟钢筋循环性能，混合硬化参数见表2，结果比较见图7。模拟结果与试验结果吻合良好。由此证明本文模拟方法的可行性。

表2 混合硬化参数Tab.2 Parameters of combined hardening

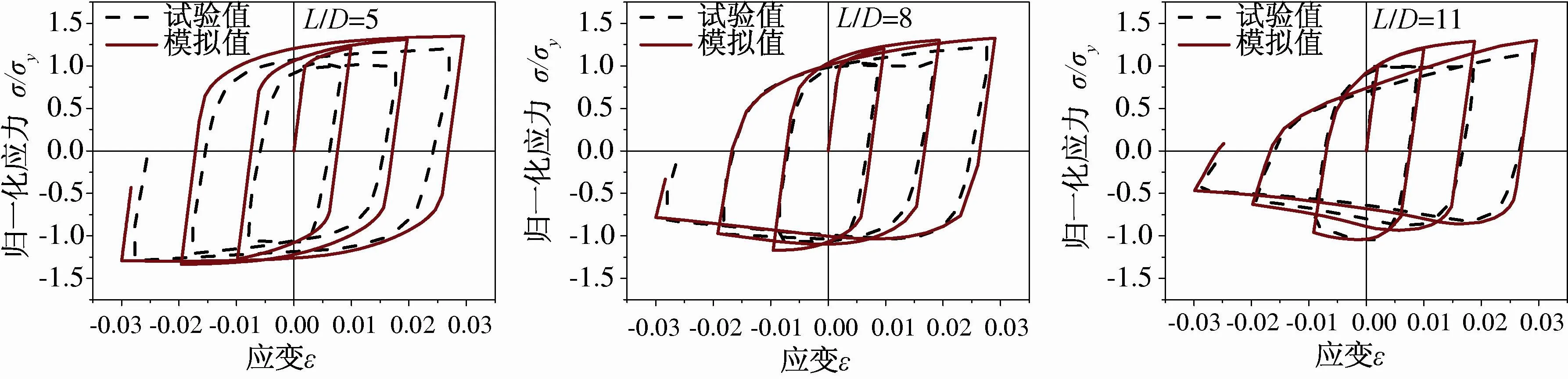
图7 模拟结果与试验结果［19］比较Fig.7 Comparison of simulated and experimented results［19］

2.1 L／D对钢筋循环性能的影响

如图8所示，数值仿真了相同L／D下四种不同直径钢筋的拉压循环曲线，从数值模拟结果来看，影响钢筋循环性能的主要影响因素是L／D，与直径无关，该结论在其他学者的试验中得到证实［1，19］。当钢筋L／D≤5时，钢筋的循环曲线是基本对称的，如图9所示，拉伸（或压缩）应力达到屈服以后下一个半循环中弹性段减小，屈服应力有明显降低，这反映出典型的包辛格效应。钢筋滞回曲线绕原点呈径向扩张趋势，这反映了L／D≤5时钢筋在循环荷载作用下主要表现出各项同性硬化。

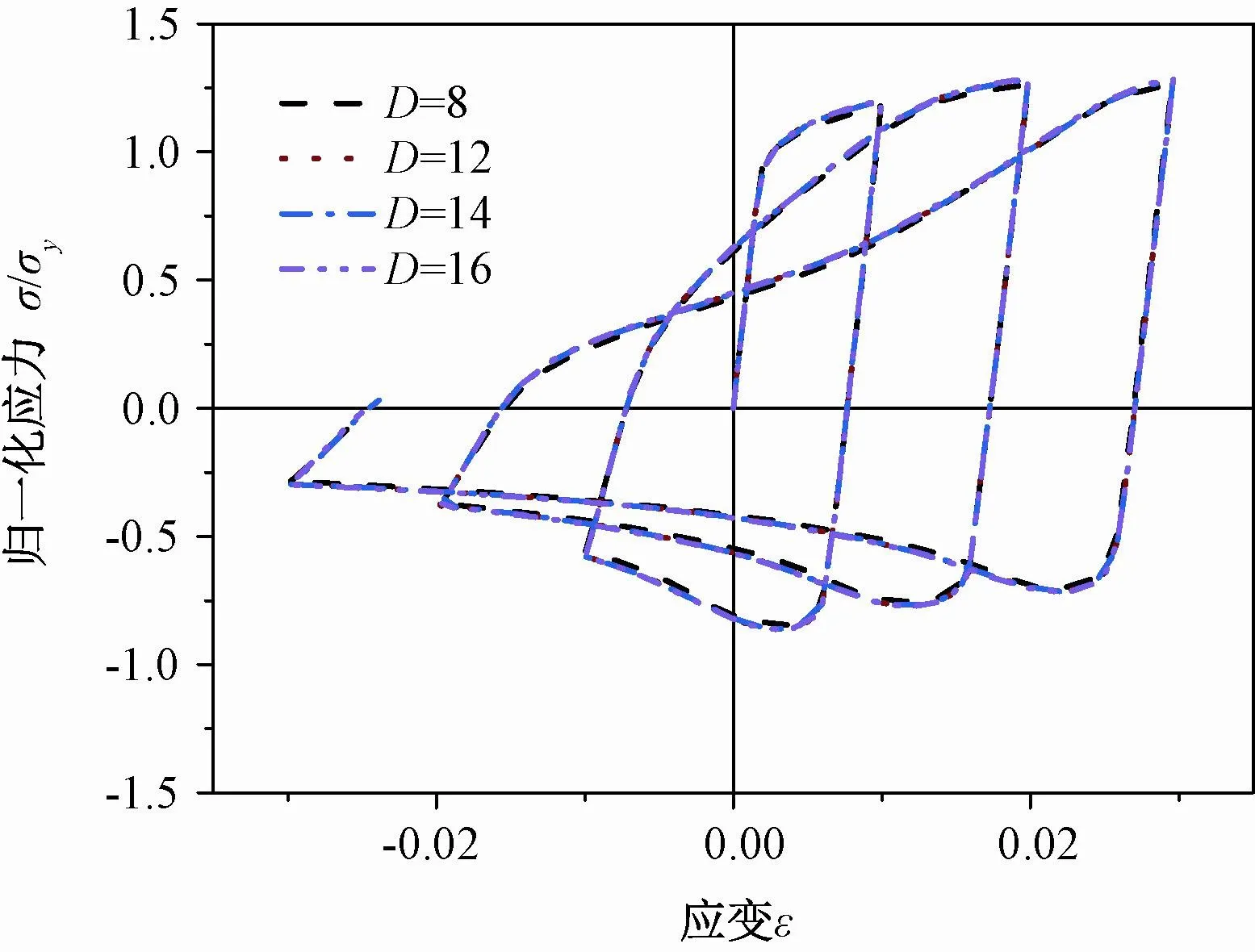
图8 L／D＝15不同直径钢筋循环曲线Fig.8 Cyclic curves for different diameters when L／D＝15

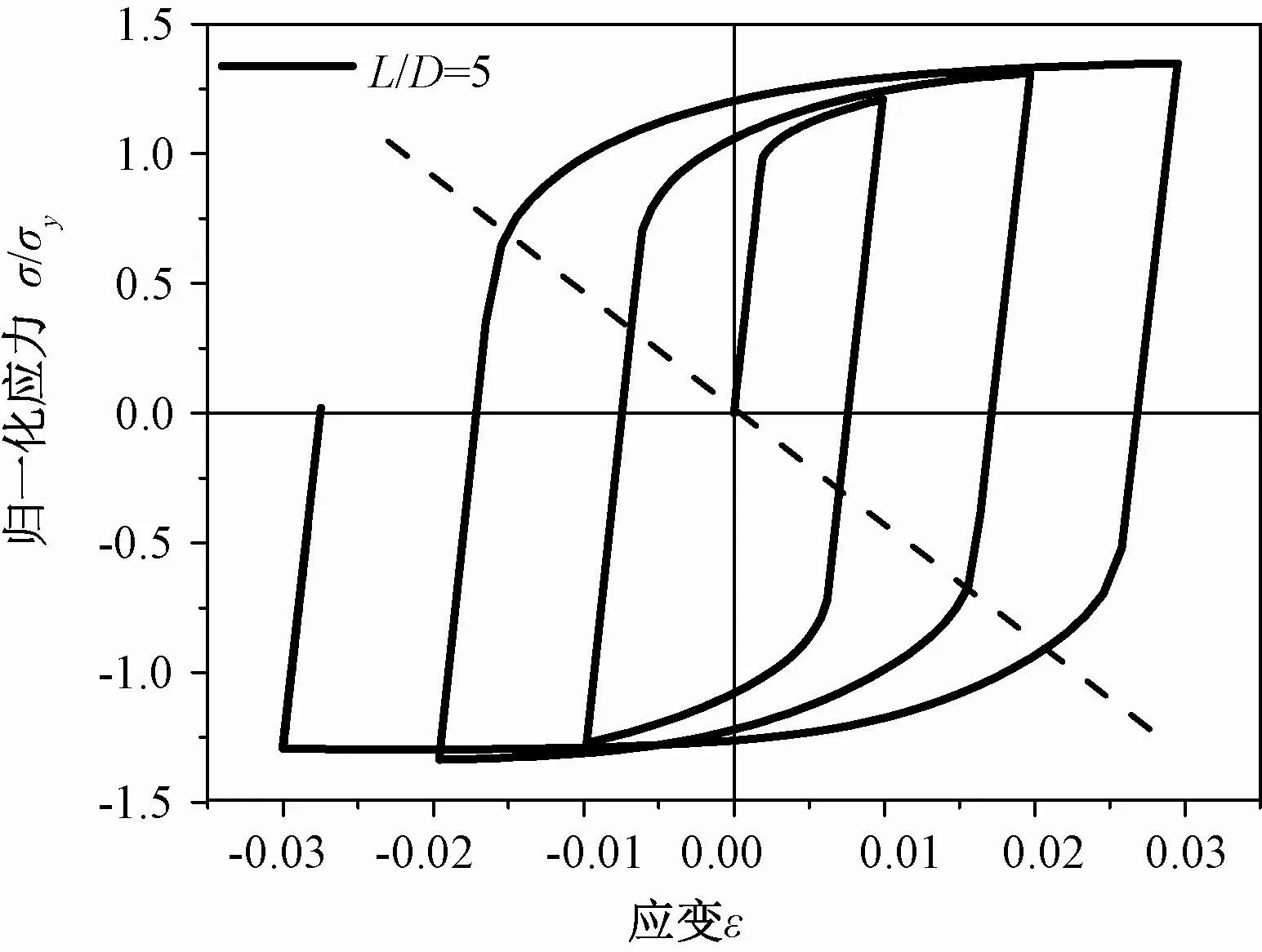
图9 L／D＝5时钢筋循环曲线Fig.9 Cyclic curves when L／D＝5

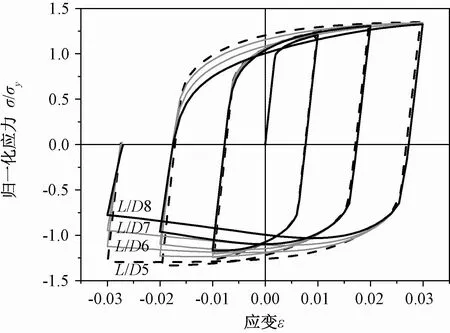
图10 L／D≥5时钢筋循环曲线Fig.10 Cyclic curves when L／D≥5

L／D＞5时循环曲线不再对称，由典型的材料滞回曲线转化为典型的长细梁滞回曲线。图10和图11分别给出了L／D为5～8时钢筋拉压循环曲线和钢筋强度及刚度变化特征，具有如下特点：

（1）循环过程中每个半循环曲线特征是固定的：每个半循环曲线开始都是线弹性段，最终是趋于一条渐近线的非线性段。据推断所有半循环曲线压缩和拉伸的渐近线具有相同的斜率。随着L／D的增加，拉伸和压缩曲线由于屈曲的发生变得不再对称，拉伸曲线渐近线斜率在增加，然而压缩曲线渐近线斜率在减小。

（2）受压时强度的退化与钢筋L／D的增加无关：双线性包络线交叉点处应力值大致保持不变。

（3）根据往复加载过程中拉压转换处的曲线斜率可以看出，钢筋由受拉向受压反转点处刚度保持恒定，而在由受压向受拉反转点处刚度随着加载最大应变的增加而逐渐减小，并且随着L／D的增加该现象更加显著。

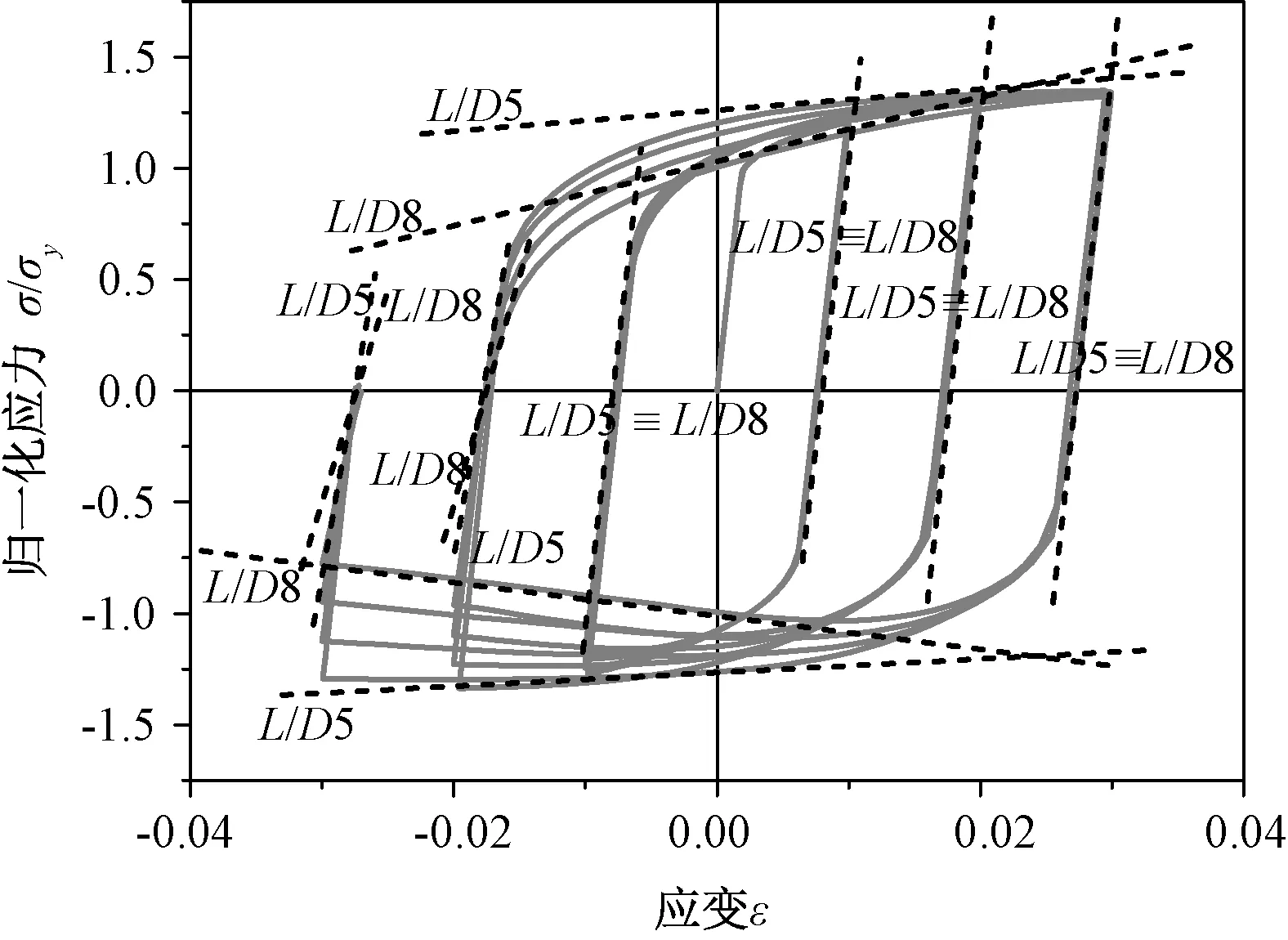
图11 L／D≥5时钢筋的屈曲和刚度退化Fig.11 Buckling and stiffness damage when L／D≥5

L／D＞8时，纵向受力钢筋循环曲线和钢筋强度及刚度变化特征如图12和图13所示。钢筋循环曲线特征如下：（1）每个半循环段曲线的曲率符号开始发生变化时，曲线都有一个拐点。屈曲对受压软化段曲线影响非常重要，随着L／D的增加，受压卸载段曲线斜率在减小，当L／D等于100时，受压卸载段曲线斜率大致为一条水平线。（2）从第一个循环到第三个循环随着循环幅值的增加，受压卸载时刚度损伤出现，并且随着L／D的增加这种现象更加明显，受拉卸载时刚度保持恒定。

2.2 加载方式对循环性能的影响

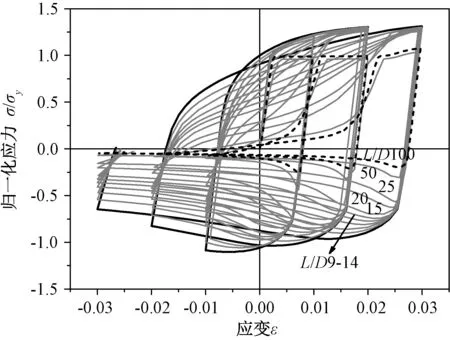
图12 L／D＞8时钢筋循环曲线Fig.12 Cyclic curves when L／D＞8

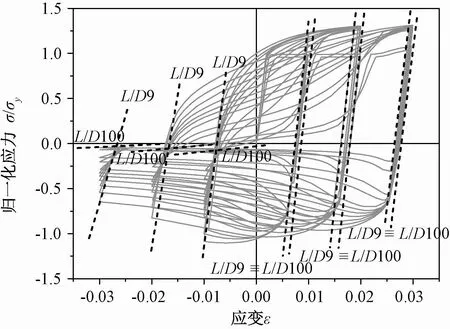
图13 L／D＞8钢筋的屈曲和刚度退化Fig.13 Buckling and stiffness damage when L／D＞8

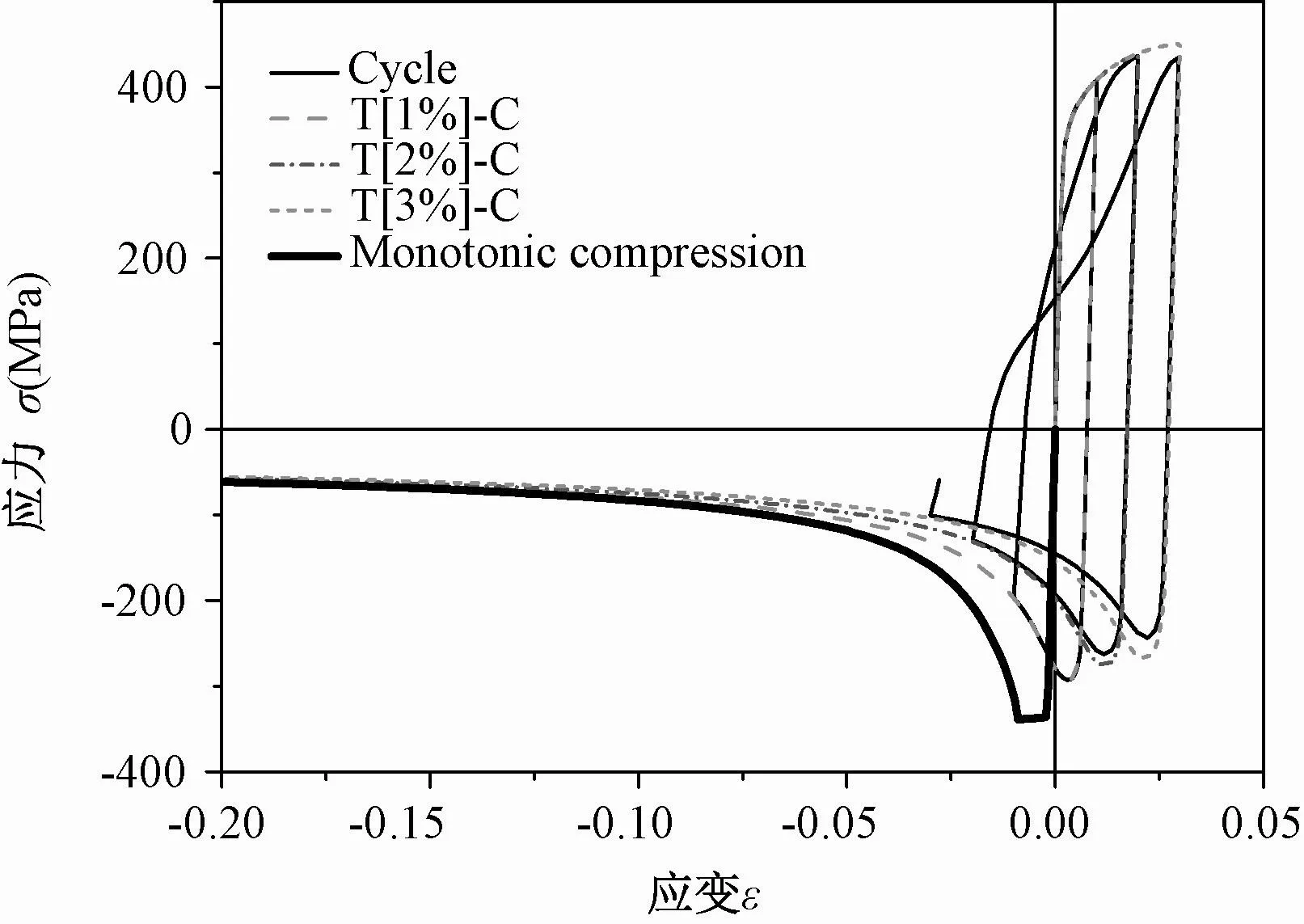
图14 L／D＝15模拟结果比较Fig.14 Comparison of simulated results when L／D＝15

为研究不同加载方式下钢筋的拉压循环响应，数值仿真钢筋承受不同的拉压应变，结果如图14所示，其中T［1%］－C、T［2%］－C、T［3%］－C表示受拉应变达到1%、2%、3%以后反向压缩。对于L／D为15的钢筋，可以发现滞回曲线与其他曲线压缩软化段的渐近线相同。另外，从图14中还可以清楚地看出在循环荷载作用下，钢筋的强度和刚度退化受到塑性变形和循环加载双重影响，这与Dodd-Restrepo Posada［20］研究结果基本一致，并且符合Cosenza-Manfredi［21］等的研究结论，其认为钢筋的功能性损伤可能是由于延性功能和能量功能的结合效应。

2.3 历史荷载对受压强度的影响

为考虑历史荷载对钢筋轴向压缩强度损失的影响，主要是前期受到拉伸，进行一些模拟。结果如图15所示，0．5εy与0．9εy所代表的曲线与单调受压曲线完全重合，然而T［1%］－C所代表的的曲线明显低于前三者。上述结果说明强度损失仅当应变超过屈服应变时才会发生，弹性拉伸后受压时强度保持不变。其中，0．5εy与0．9εy分别表示先拉伸0.5和0.9倍屈服应变后反向压缩，T［1%］－C表示先拉伸1%应变后反向压缩。

图15 L／D＝10模拟结果比较Fig.15 Comparison of simulated results when L／D＝10

3 结论

本文通过ABAQUS有限元软件对钢筋混凝土构件中的纵向受力钢筋在压缩以及拉压循环作用的屈曲行为和力学性能进行数值仿真分析，主要得到以下结论：

（1）钢筋的压缩性能取决于L／D，与屈服强度无关，若L／D不大于7，钢筋延性性能非常好，随着L／D的增加，延性逐渐降低，并且在大于20以后会发生弹性屈曲。

（2）钢筋的循环性能受到加载历史、塑性变形、循环加载以及L／D影响。弹性变形后钢筋的力学性能与之前没有变化，但在塑性变形后钢筋力学性能发生明显改变。钢筋强度和刚度的退化受到塑性变形和循环加载双重影响。L／D不大于5时钢筋在循环荷载下的应力－应变曲线基本对称，但在L／D大于8以后，应力－应变曲线明显不再对称，并且随着L／D的增加，受压卸载后由于屈曲的发生钢筋的刚度在减小。

［1］ Monti G，Nuti C.Nonlinear cyclic behavior of reinforcingbarsincludingbuckling.Journalof Structural Engineering，1992，118（12）：3268－3284.

［2］ Gomes A，Appleton J.Nonlinear cyclic stress-strain relationship of reinforcing bars including buckling［J］.Engineering Structures，1997，19（10）：822－826.

［3］ Dhakal R P，Maekawa K.Modeling for postyield buckling of reinforcement［J］.Journal of Structural Engineering，2002，128（9）：1139－1147.

［4］ Dhakal R P，Maekawa K.Path-dependent cyclic stress-strain relationship of reinforcing bar including buckling［J］.Engineering Structures，2002，24（11）：1383－1396.

［5］ Kunnath S K，Heo Y A，Mohle J F.Nonlinear uniaxial material model for reinforcing steel bars［J］. Journal of Structural Engineering，2009，135（4）：335－343.

［6］ 杨红，谢琴，张吉庆，等.考虑屈曲影响的钢筋本构修正模型及试验验证［J］.土木工程学报，2015，48（10）：21－29.

［7］ 方自虎，简旭阳，周尧，等.考虑屈曲的钢筋滞回模型［J］.武汉大学学报：工学版，2016，49（2）：254－258.

［8］ 蒋凤昌，朱慈勉.混凝土柱中箍筋锈蚀影响纵筋压屈行为分析［J］.东南大学学报：自然科学版，2008，38（2）：279－282.

［9］ 蒋凤昌，朱慈勉，薛剑胜，等.锈蚀钢筋压屈名义本构关系的试验研究及应用［J］.东南大学学报：自然科学版，2010，40（4）：816－821.

［10］ Kashani M M，Lowes L N，Crewe A J，et al. Phenomenologicalhystereticmodelforcorroded reinforcing bars including inelastic buckling and lowcyclefatiguedegradation［J］.Computers＆Structures，2015，156：58－71.

［11］ Massone L M，López E E.Modeling of reinforcement global buckling in RC elements［J］.Engineering Structures，2014，59：484－494.

［12］ Dhakal R P，Maekawa K.Reinforcement stability and fracture of cover concrete in reinforced concrete members［J］.Journal of Structural Engineering，2002，128（10）：1253－1262.

［13］ Kashani M M，Lowes L N，Crewe A J，et al. Nonlinear fibre element modelling of RC bridge piers considering inelastic buckling of reinforcement［J］. Engineering Structures，2016，116：163－177.

［14］ Zong Z，Kunnath S.Buckling of reinforcing bars in concrete structures under seismic loads［C］／／The 14th World Conference on Earthquake Engineering. 2008.

［15］ 杨红，张洛，张和平.考虑纵筋屈曲及疲劳损伤的钢筋混凝土柱抗震性能试验研究与非线性分析［J］.建筑结构学报，2013，34（11）：130－140.

［16］ Bai Y.Behavior and modeling ofRC columns confined with large-rupture strain FRP composites［D］.The Hong Kong Polytechnic University，2014.

［17］ Cosenza E，Prota A.Experimental behaviour and numerical modelling ofsmooth steelbars under compression［J］.Journal of Earthquake Engineering，2006，10（3）：313－329.

［18］ Chaboche J L.Time-independent constitutive theories for cyclic plasticity［J］.International Journal of plasticity，1986，2（2）：149－188.

［19］ Prota A，De Cicco F，Cosenza E.Cyclic behavior of smooth steel reinforcing bars：experimental analysis and modeling issues［J］.Journal of Earthquake Engineering，2009，13（4）：500－519.

［20］ Dodd L L，Restrepo-Posada J I.Model for predicting cyclic behavior of reinforcing steel［J］.Journal of Structural Engineering，1995，121（3）：433－445.

［21］ Cosenza E，Manfredi G.Damage Analysis of RC Elements Subjected to Seismic Loads［J］.5th US，1994.

Numerical Simulation Analysis of Reinforcement Bars Considering Buckling Behavior

Cao Yanhui，Jia Junfeng
（College of Architecture and Civil Engineering，Beijing University of Technology，Beijing 100124，China）

For the purpose of assessing mechanical performance of longitudinal reinforcement bars considering buckling behavior，the ABAQUS finite element software was used to simulate the change of strength and stiffness of longitudinal reinforcement bars with different length-to-diameter ratio（L／D）under axial compressing and cyclic loading.The effect of loading history and loading mode on the mechanical behavior of reinforcement bars was also taken into consideration.As the results show，the buckling behavior exerts a significant effect on the mechanical performance of longitudinal reinforcement bars，and the axial compressing behavior of longitudinal reinforcement bars is determined by the L／D parameter，rather than by the steel yield strength.Under cyclic loading，the mechanical performance of reinformcemant bars is influenced by loading history，plastic deformation，cumulative damage and L／D．The compressive strength loss of reinforcement bars would occur when the pre-tensile strain exceeds yielding strain.Plastic deformation and cyclic loading together result in cumulative damage of reinforcement bars.Buckling behavior of reinforcement bars leads to deterioration of the bars′strength and stiffness，and the degree of the deterioration is proportionate to the increasing L／D parameter.This research is hoped to help evaluate the mechanical performance of reinforced concrete elements.

buckling of reinforcement bar；length-to-diameter ratio（L／D）；compressing behavior；cyclic behavior；numerical simulation

TU392.2

：A

：1673－8047（2017）02－0009－08

2017－01－21

北京市教委科技计划项目（KM201510005020）

曹艳辉（1990—），男，硕士研究生，主要从事桥梁抗震方面的研究。

贾俊峰（1982—），男，博士，副教授，主要从事桥梁抗震方面的研究。