根植课本，耕耘课堂——高三一轮复习《椭圆》的教学实践与思考

江苏省张家港市暨阳高级中学 童先峰

根植课本，耕耘课堂
——高三一轮复习《椭圆》的教学实践与思考

江苏省张家港市暨阳高级中学 童先峰

乔治·波利亚说：“也许你要解答的题目很平常，但是它如果激起了你的好奇心，并使你的创造性发挥出来，而且你用自己的方法解决了它，那么你就能经历那种紧张的状态，而且享受那种发现的喜悦……”这段话说明在平时的教学中，我们教师要采用“遵循课程标准、紧扣考试说明、根植课本素材、立足教考合一、突出思想方法、耕耘优效课堂”的组织方式开展探究教学活动，依托经典题，给学生提供探究问题的平台，实现“授之以渔”，为学生的终身学习奠定良好的知识基础和思维保障。

下面，笔者以高三一轮复习圆锥曲线《椭圆》一课为例，就教学过程中如何让学生充分经历知识发现、发生、发展的探究过程与同行交流，敬请指正。

一、基本情况

授课对象：学生系高三物生实验班，学习能力较强，对数学学科兴趣盎然。

教学目标：（1）探索发现不同方式刻画椭圆的内在联系并进行适度拓展；（2）激发和培养学生的探究精神及学好数学、用好数学的意识。

二、片段实录

1.创设情境

引例：已知A（-3,0），B（3,0），直线PA,PB相交于点P，且它们的斜率之积为，求点P的轨迹方程，并说明此轨迹是何种曲线。

【设计意图】通过对课本习题的探求，带着一份亲切和朴实，激发学生解决问题的信心与兴趣，使学生顺利进入探究问题的环节，有助于学生打开思维。

2.探究拓展

（1）追根溯源：问题1：你能由此将问题一般化，形成新的数学问题吗？

【设计意图】通过师生共同探究发现椭圆除了高二时学的“平面内到两个定点的距离之和是一个常数”定义外，还可以通过“平面内到两定点的斜率之积为常数”来刻画，让学生学有所得，学有所获，进一步激发探究问题的勇气和力量。

（2）探究关联：问题2：接下来让我们一起再来对椭圆定义和推导过程进行一次反思和探索，看能否有所发现？

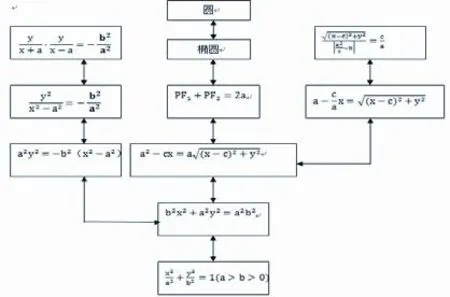
【设计意图】将问题情境形成椭圆的崭新命题有机蕴含于原来推导椭圆标准方程的过程，并衍生出圆锥曲线（椭圆）的统一定义，从而帮助学生发现了它们之间的内在联系，体会在推导椭圆标准方程的过程中，因化简路径的不同，所最终呈现的结论流芳溢彩，各有千秋，而后将圆与椭圆方程进行类比，从另一层面更好地说明椭圆的斜率定义的必然。

（3）逆向探究：问题3：我们再回到问题1，接下来一起进行逆向研究，请思考问题1的逆命题是什么？结论是否成立？

（4）深度探究：问题4：如果将结论中的长轴换成经过原点的任意一条弦，结论是否成立？

（5）延伸探究：问题5：请同学们课后继续思考：能否将上述结论类比迁移到双曲线中?

【设计意图】以探索和应用椭圆的性质为载体，逐层深入，引导学生经历椭圆性质的生成和应用过程，使知识与能力得到升华，有助于学生形成良好的思维习惯和数学素养。

三、教学反思

高三数学复习时间占了整个高中教学近三分之一的时间，复习课质量的高低直接影响了学生数学能力的形成。《普通高中数学课程标准（实验）》明确提出：“学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课还应倡导自主探索，动手实践、阅读自学等学习方法的转变”。因此笔者感到，要真正改变学生的学习方式，提高学生的探究能力，必须将数学探究教学植根于日常教学活动中，让探究教学成为高三复习“常态”。

1.把握问题起点，突出能力立意

探究活动起点太低,学生会觉得没有探究的必要，不能激发学生探究的兴趣；起点太高，学生无法在已有的知识方法与所要探究的对象之间建立有效的联系，从而失去探究的信心。因此，在本节课探究设计中，笔者从课本的一道习题出发，通过轨迹方程中数据的关系提出问题，继而引导学生反思椭圆标准方程的推导过程，进而得到椭圆斜率定义，并揭示出三个定义之间的联系：实质是源于方程的不同形式。这样的设计也符合学生认知的“最近发展区”原则，使大多数学生能主动参与到探究活动中来，从而让大多数学生实现“跳一跳能摘到”，而不是仅针对少数数学尖子生而设计。

2.强化探究设计，引领知识延展

合情推理是数学发现的重要途径，培养学生通过归纳、类比、一般化、特殊化等思维方式去提出新问题是探究的重要途径。本节课还通过椭圆与圆的类比，发现椭圆的斜率定义与圆的性质的内在联系，充分揭示知识之间的内在联系，引发学生通过归纳、类比、一般化等方式不断提出问题、解决问题并将探究成果应用到高考题的解决中去，激发学生对这些性质的进一步研究和探索的兴趣，同时，还可以在很大程度上减少探究的盲目性，提高学生的探究效率。

3.注重思想方法，耕耘优效课堂

《普通高中数学课程标准（实验）》明确提出，教师应成为学生进行数学探究的组织者、指导者、合作者，教师应该为学生提供较为丰富的数学探究课题的案例和背景，引导和帮助而不是代替学生发现和提出问题。在本节课中，笔者紧紧围绕椭圆定义这个最基本的核心知识点，对其进行进一步的研究和探索，在整个探究过程中，教师主要贡献是为学生攀登思维高峰搭建好“脚手架”,较好地体现了数学教学的目的在于通过学习数学知识，培养学生发现问题、分析问题和运用所学数学知识解决问题的能力，从而不断提高数学素养。