考虑非共轴特性的吸力桶基础竖向荷载-变形特性研究
罗 强,冯 娜,贾 虎
(1.南阳师范学院 土木建筑工程学院, 河南 南阳 473061;2.河南工业职业技术学院 经济管理学院, 河南 南阳 473000 )
考虑非共轴特性的吸力桶基础竖向荷载-变形特性研究
罗 强*1,冯 娜2,贾 虎1
(1.南阳师范学院 土木建筑工程学院, 河南 南阳 473061;2.河南工业职业技术学院 经济管理学院, 河南 南阳 473000 )
土体在剪切变形过程中会产生较为显著的主应力方向旋转,主应力方向与塑性主应变增量方向将呈现出显著的差异即非共轴现象.采用砂土非共轴弹塑性本构模型,以吸力式桶形基础为研究对象,研究土体主应力方向旋转和非共轴角度的变化规律,探讨非共轴特性对地基荷载-位移关系的影响.研究结果表明:在竖向荷载作用过程中,土体主应力方向处于单调旋转状态,吸力桶形基础高径比对土体主应力方向的旋转规律(方向、速率和极值)有显著影响.非共轴特性对荷载-位移关系的发展趋势有显著的减缓滞后作用,该作用在地基变形中期比较显著.随着高径比的增加,非共轴特性逐渐显著,该特性对地基竖向荷载-位移关系的影响逐渐明显.
非共轴理论;主应力方向;吸力桶;本构模型;数值分析
0 引 言
吸力式桶形基础适用于深、浅海域,地质条件可以为砂性土或软黏土,在海上采油平台和风力发电工程领域有广泛的应用前景.目前,对桶形基础的研究还很不充分,特别是针对复杂荷载(风、波浪荷载)作用下土体与桶形基础的相互作用机理还需进行深入的研究.
目前,国内外学者主要采用数值计算、理论分析和模型试验的方法对桶形基础的力学特性进行研究.武科等[1]对桶形基础承载性能进行了弹塑性有限元数值分析,对基础结构承载力特性进行研究.张宇等[2]通过数值计算和模型试验对基础的受力机理进行了分析.武科等[3]基于弹塑性极限分析上限法建立了一种极限分析模型,并通过有限元数值分析进行了验证.鲁晓兵等[4]通过模型实验研究了饱和砂土中桶形基础的静力承载特性.Bransby等[5]、Gourvenec等[6]对于水平荷载、竖向荷载和弯矩共同作用的共面复合加载条件下的地基承载力进行了模型试验和数值分析.然而,上述研究工作均假定主应力方向在剪切变形过程中是固定的,没有考虑主应力方向旋转对土体力学特性的影响.在实际工程中,地震、波浪和风荷载会使吸力桶周围土体产生显著的主应力方向旋转,并产生相应的塑性变形和力学特性变化[7-8].沈瑞福等[9]对砂土进行了一系列不排水剪切试验,其分析结果表明土体强度在主应力方向旋转过程中明显降低,降低幅度可达到15%.姚仰平等[10]对饱和砂土试样进行了大量动力试验,提出主应力方向旋转对土体的变形与强度特性具有重要影响.由上述分析可知,如果不考虑主应力方向的旋转,那么,对吸力桶基础荷载-变形特性的研究分析将欠缺完整性和准确度.
近些年,相关学者在研究土体主应力方向旋转规律时,发现主应力方向与塑性主应变增量方向之间存在一定的差异,即非共轴现象[11-12].在传统共轴弹塑性本构理论的基础上,相关学者提出了一些非共轴本构理论,探讨了非共轴特性对土体力学特性的影响[13-14].目前,非共轴本构理论主要应用于一些简单结构的数值分析研究,其在复杂工程中的应用较为欠缺.对于吸力桶这种结构形式和荷载情况均比较复杂的工程结构,目前还缺少关于非共轴特性的研究.
针对非共轴特性对吸力桶基础荷载-变形特性的影响,本文在屈服角点非共轴理论[15]的基础上建立一种砂土非共轴弹塑性本构模型[16],以反映主应力方向的旋转变化,对主应力方向和塑性主应变增量方向进行计算,揭示非共轴现象的产生过程及其对土体力学特性的影响.基于大型通用软件ABAQUS平台,对非共轴模型有限元二次开发,以吸力桶基础竖向荷载-变形特性为数值分析对象,研究土体主应力方向的旋转变化规律、非共轴角度的变化规律,探究非共轴特性对吸力桶地基荷载-变形特性的影响.
1 非共轴理想弹塑性本构模型
根据屈服角点结构非共轴弹塑性理论[15],应变增量可采用以下形式表达:
由表2可以看出,水浸、酸浸过程中铂的损失量小。萃钯余液中主要杂质元素为碲和硒,经加碱中和后,料液中碲、硒浓度大幅下降,其中碲由30.15g/L下降至2.69g/L,硒由3.52g/L下降至1.94g/L,但铂浓度变化较大,由0.69g/L下降值0.46g/L。
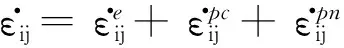
ε.ij=ε.eij+ε.pcij+ε.pnij
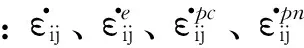
(1)
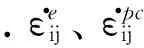
.ε.eij、ε.pcij
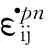
ε.pnij
式中分别为应变增量、弹性应变增量、共轴塑性应变增量和非共轴塑性应变增量可由传统弹塑性本构理论求得.非共轴塑性应变增量可由下式求得:
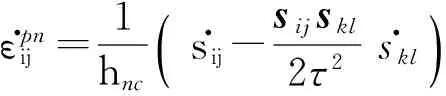
ε.pnij=1hnc(s.ij-sijskl2τ2s.kl)
(2)
hnc=hnc0[1-e(-16εp)0.7]-1
(3)
(2)在地基变形初期,非共轴现象比较显著;随着变形的增加,非共轴现象逐渐减弱.
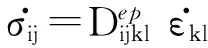
σ.ij=Depijklε.kl
(4)
(5)
(6)
式中:K、G分别为体积、剪切弹性模量;D为弹塑性刚度矩阵;δij为克罗内克符号;R表示塑性势流动方向;l表示屈服面法向;E表示弹性刚度矩阵;Nijkl为与非共轴因素相对应的矩阵项[16].
通过有限元程序ABAQUS里面的用户材料子程序UMAT,采用显式积分算法和自动分步相结合的积分方法,对非共轴本构模型进行数值积分,详见文献[16].
2 桶形基础荷载-变形特性分析
在竖向荷载作用下,对不同高径比的桶形基础进行数值分析.首先,研究土体主应力方向的旋转变化规律,明确高径比对主应力方向的旋转范围和极值的影响.然后,在主应力方向旋转过程中,研究非共轴角度的变化规律,明确高径比和土体位置对非共轴角度的影响.最后,分析非共轴特性对地基荷载-位移关系的影响,探讨非共轴特性对计算结果的影响规律.
由图3可知,当WTP小于3 200元时,采用无阿司匹林方案(安慰剂)进行CVD一级预防相较于阿司匹林方案更具经济性的概率约为99%;当WTP约为3 500元时,无阿司匹林方案相较于阿司匹林方案更具经济性的概率约为50%,即两种方案经济性无显著差异;当WTP大于3 600元时,阿司匹林方案更具经济性的概率约为99%。
2.1 有限元模型
由图6可知:(1)竖向荷载差异在加载初期呈增长趋势;达到最大值后,差异逐渐减小.(2)随着高径比的增加,竖向荷载差异达到最大值时所对应的竖向位移逐渐增加;竖向荷载差异的最大值逐渐增加;过了最大值以后,竖向荷载差异减小的速率逐渐变小.(3)随着高径比的增加,竖向荷载差异增长阶段在整个关系曲线中所占的比例逐渐减小,然而,减小阶段所占的比例逐渐增加.(4)前述分析表明:随着高径比的增加,竖向荷载差异表现得越来越显著,即非共轴特性对吸力桶地基竖向荷载-位移关系的影响逐渐增加.
有限元模型的底面边界约束竖直方向的自由度,侧面边界约束水平方向上的自由度.桶壁内、外侧面,端部及桶顶内表面与土体之间均设置为摩擦接触对.为了保证分析对比的合理性,数值积分二次开发时选取与ABAQUS 默认值相同的荷载残留容许误差和位移修正容许误差,分别设定为0.5%和1.0%.
2.2 主应力方向旋转规律分析
由图3得到的非共轴角度发展规律在图4中仍然适用,表明高径比与非共轴角度之间的关系在桶形基础周围土体中普遍一致.
(3)随着高径比的增加,非共轴现象越来越明显.
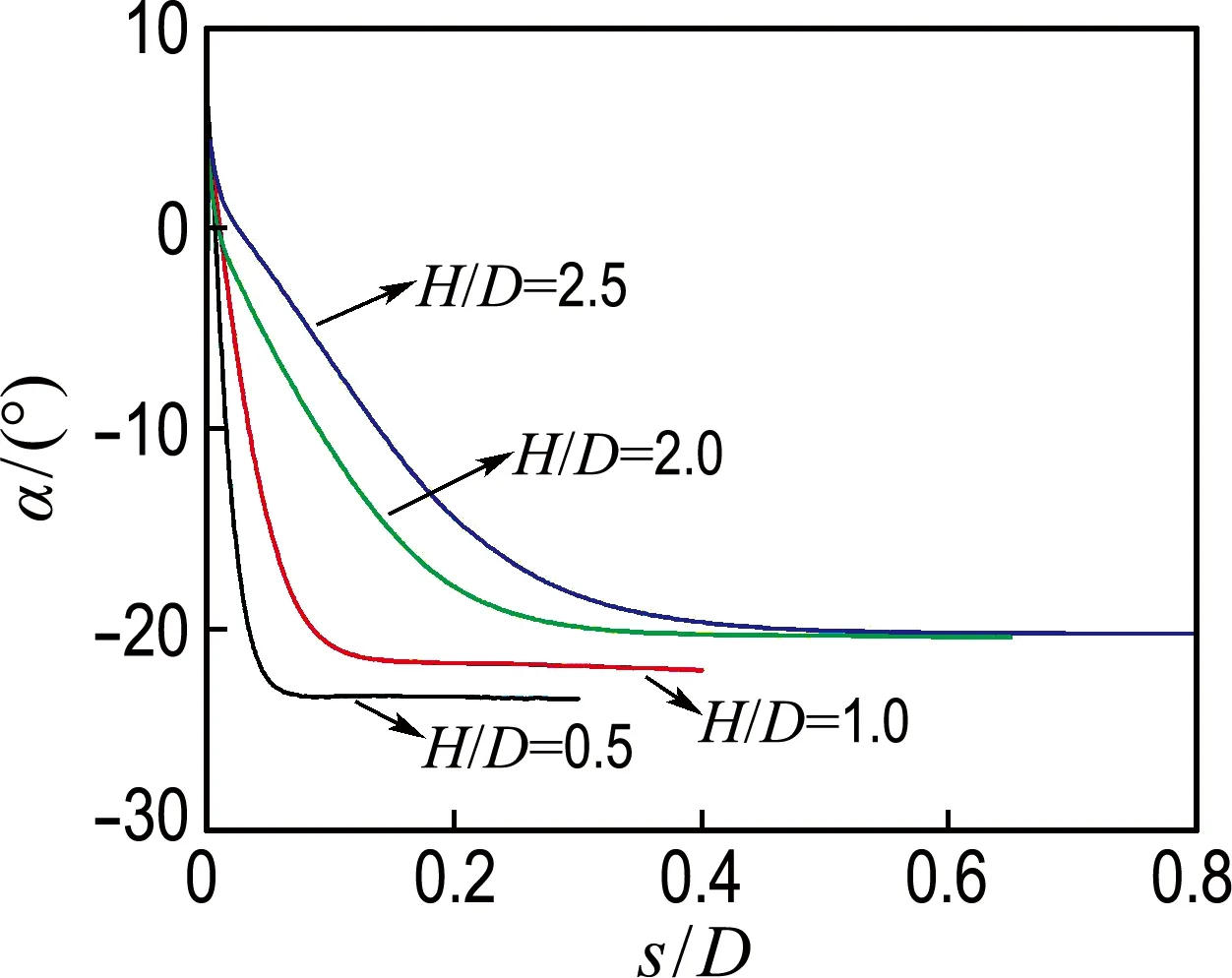
(a) 桶壁端部
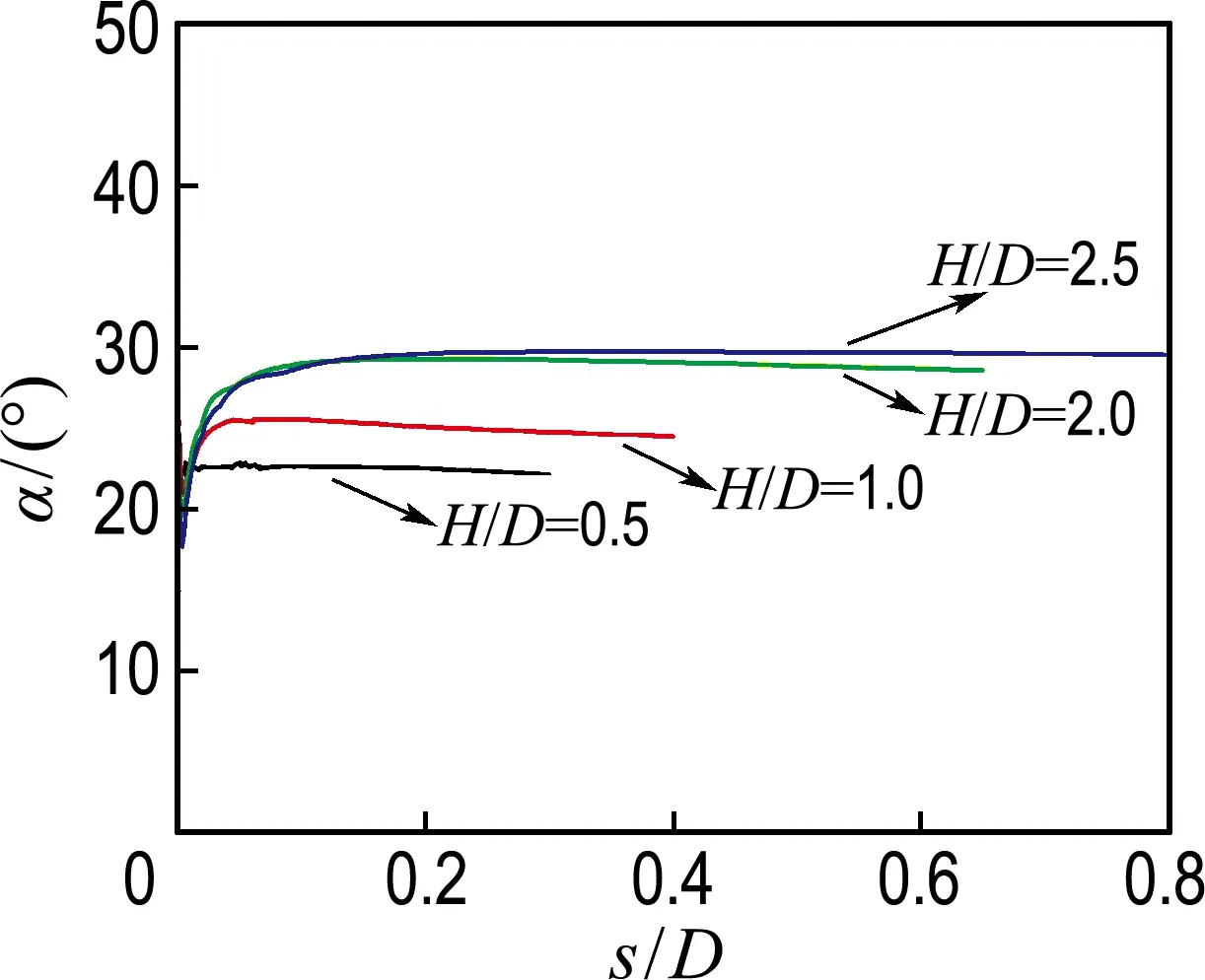
(b) 桶顶内
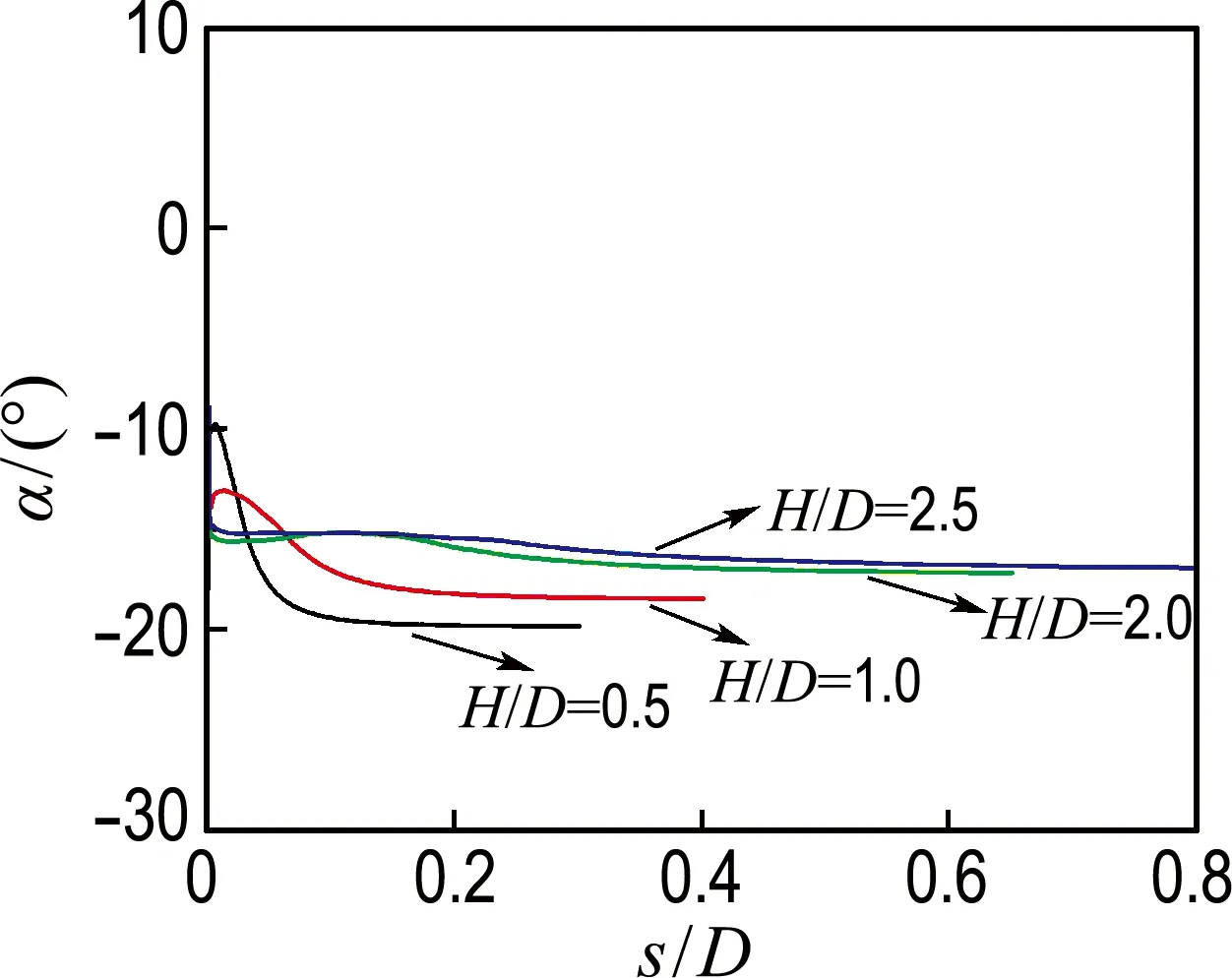
(c) 桶壁内
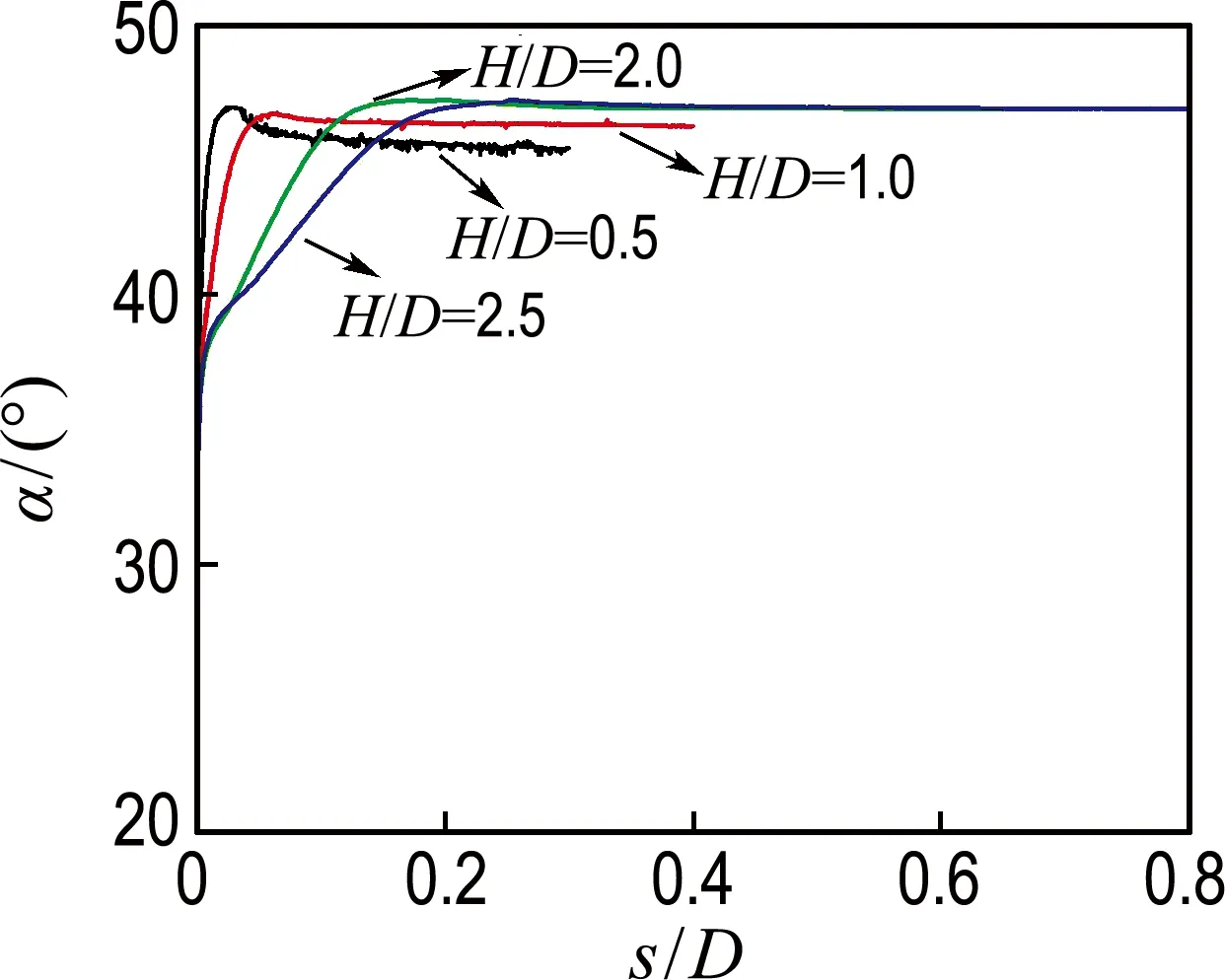
(d) 桶壁外侧
图1 土体主应力方向旋转趋势
Fig.1 Rotations trend of soil principal stress directions
上述分析表明,桶形基础高径比对土体主应力方向的旋转规律(方向、速率和极值)有显著影响.
1.3.2 样品制备 准确称取0.5000g加工好的样品于50mL的聚四氟乙烯坩埚中,用水湿润后加入5mL HCl,放在温控电热板(120℃)上,使样品初步分解,当溶液剩大约2mL时取下冷却,加入5mL HNO3和5mL HF,2mL HClO4,调节电热板温度至180℃。待整体溶液剩余3mL左右时取下稍微冷却后再加入2mLHNO3、2mLHF和1mLHClO4。当白烟冒尽时取下冷却,用水冲洗坩埚盖和内壁,并加入1mLHNO3,温热溶解残渣,然后将溶液定容至25mL的容量瓶中,摇匀待测。同时制备空白样品。
2.3 非共轴角度变化规律
2.3.1 桶壁端部土体非共轴角度变化规律 针对桶壁端部土体,在不同高径比条件下,分析最大主应力方向α、最大塑性主应变增量方向β和非共轴角度γ的变化规律,如图2和3所示.
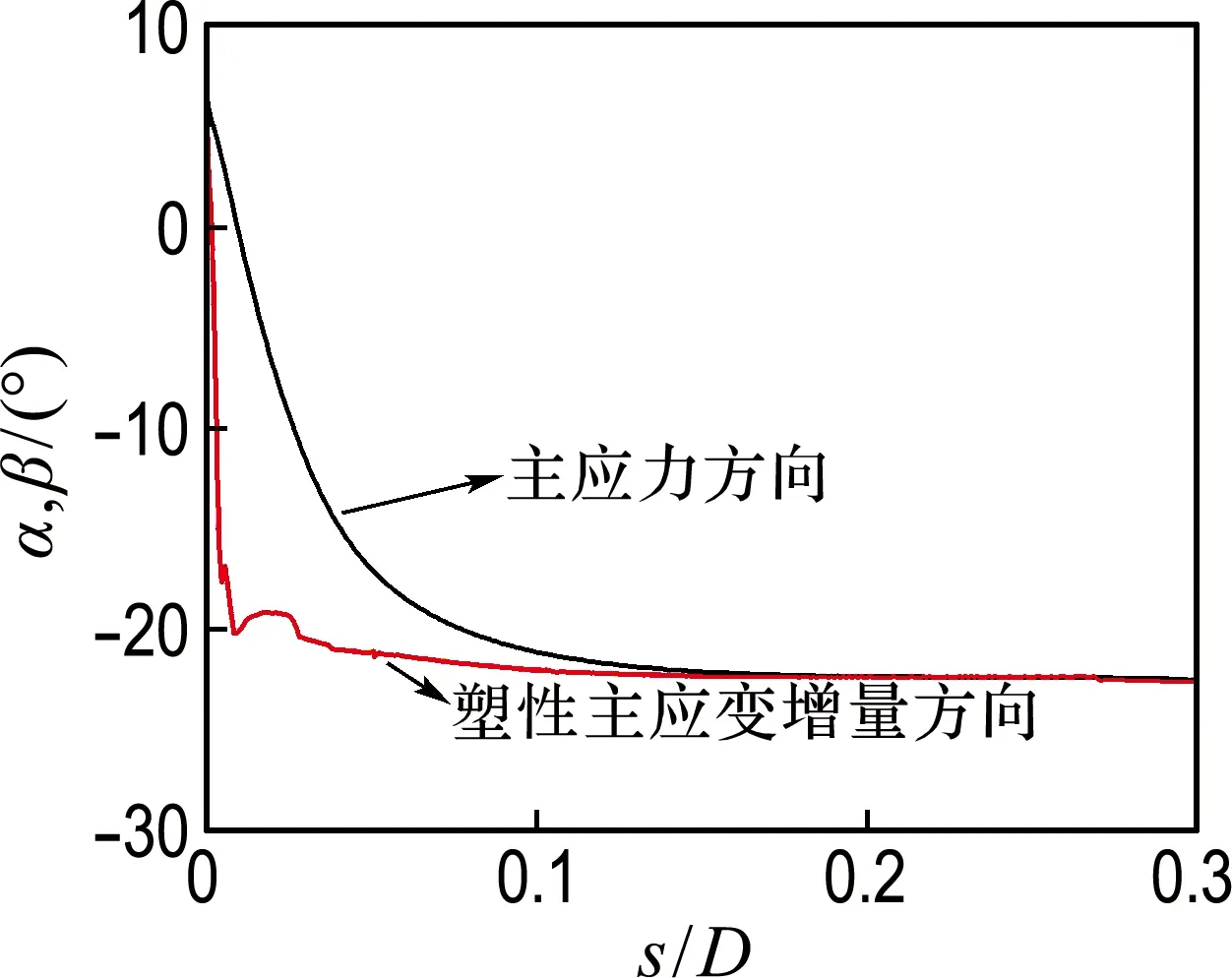
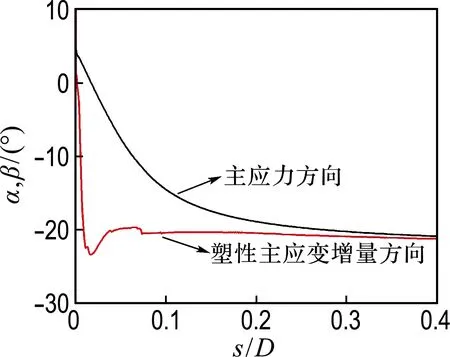
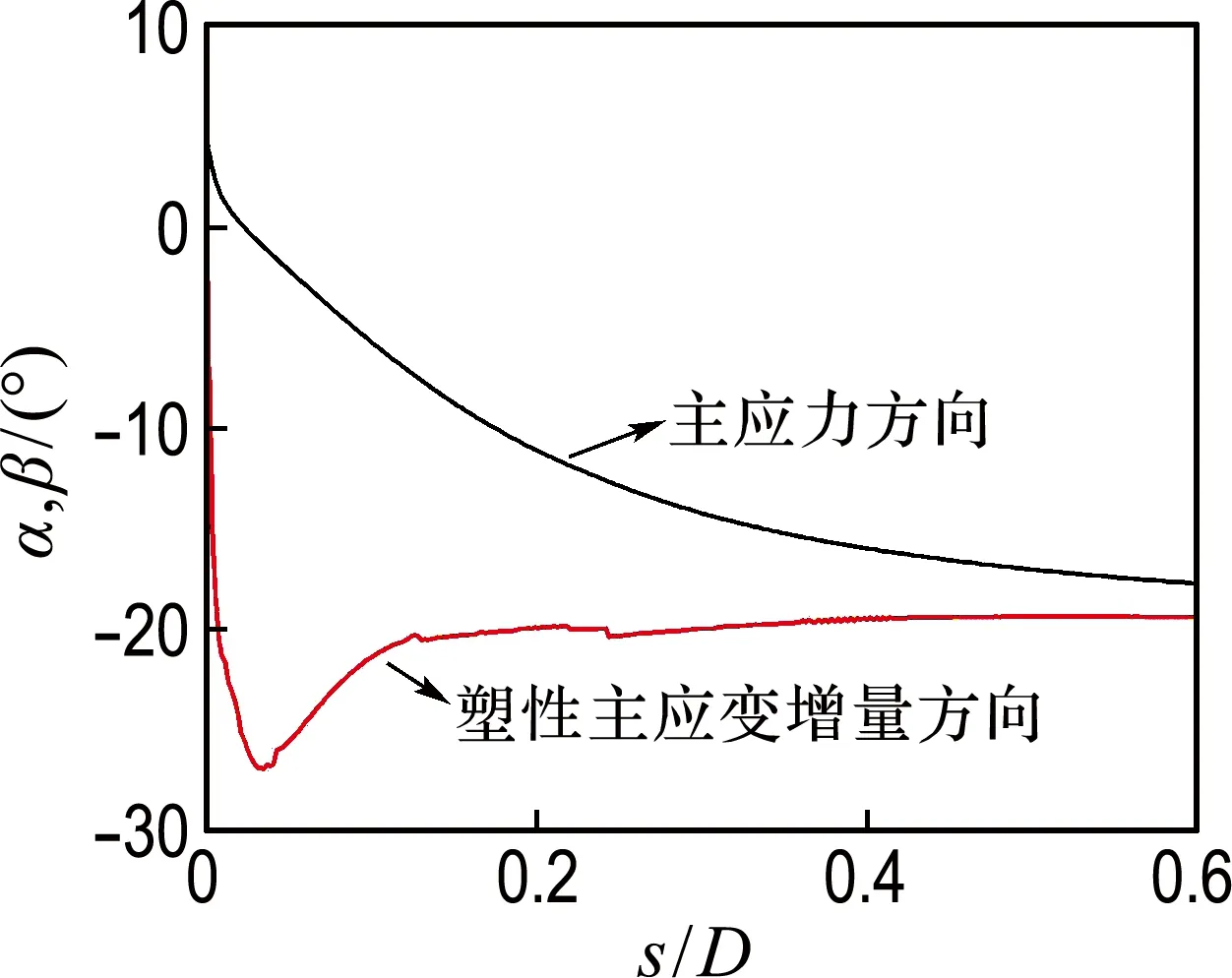
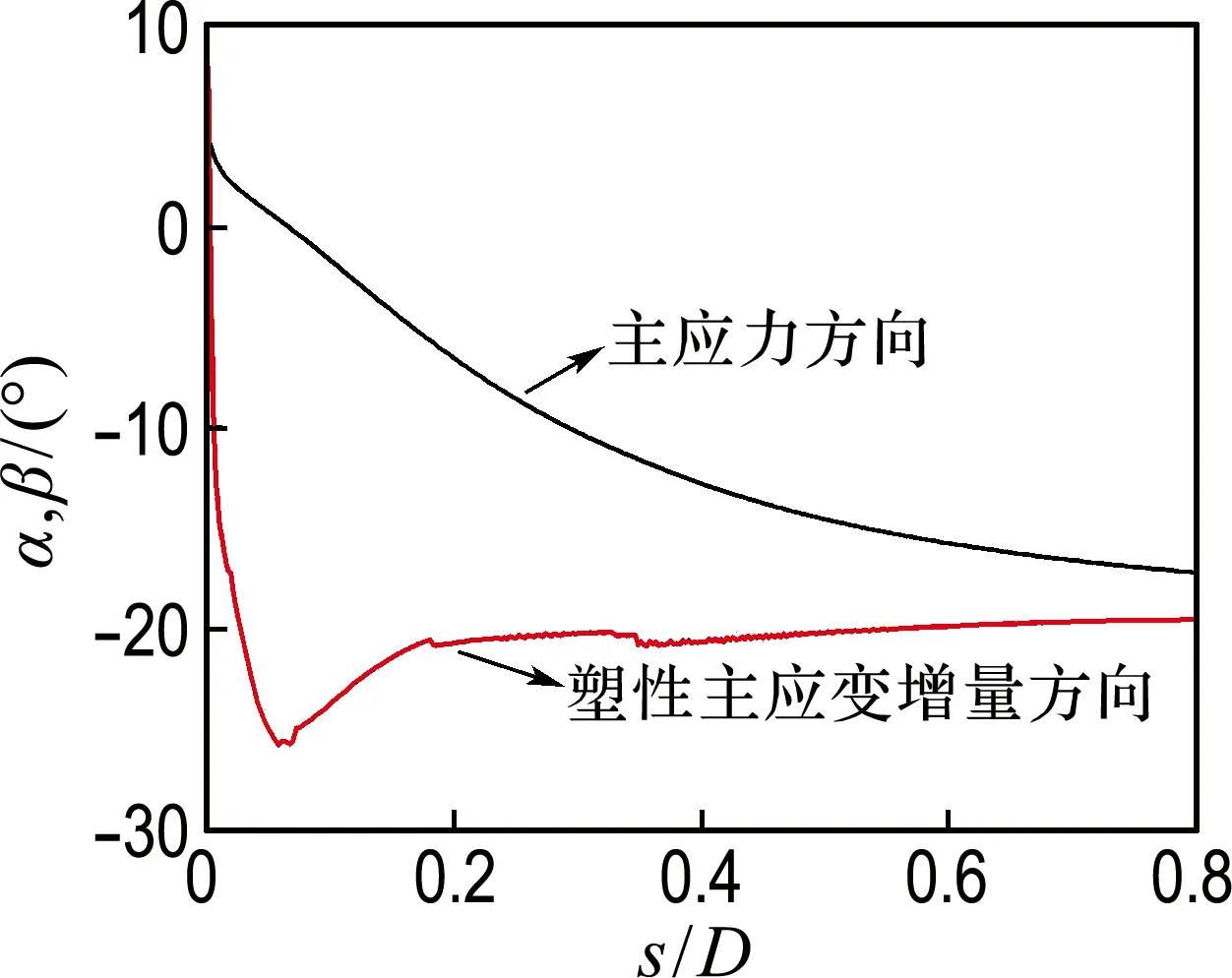
(a) H/D=0.5(b) H/D=1.0(c) H/D=2.0(d) H/D=2.5
入组标准:(1)年龄≥18岁;(2)经头颅CTA或DSA确诊为颅内动脉瘤。排除标准:(1)拒绝接受开颅夹闭手术,包括选择血管内介入手术治疗或拒绝进一步手术治疗;(2)等待手术期间动脉瘤再次破裂出血;(3)发病时头颅CT表现为蛛网膜下腔出血合并急性硬膜下血肿或颅内血肿合并急性硬膜下血肿;(4)术后继发急性硬膜下血肿;(5)缺少术后随访资料。
在图2中,主应力方向和塑性主应变增量方向的差值即为非共轴角度γ.下面,分析高径比与非共轴角度之间的对应关系,如图3所示.
图书馆的发展先后经历了传统图书馆时代——图书馆各自为主,内部空间为专业阅览室加闭架书库;计算机网络化时代——1990年前后开始图书馆计算机集成系统建设,开始文献共建共享,书库空间逐渐向开架调整,2000年之后开始大规模馆藏资源数字化和借阅藏一体化空间布局。此阶段图书馆的中心工作是以资源建设为中心,大体量新馆建设是突出性标志;复合图书馆时代——20世纪末,以数字资源发现为主导,资源增加和馆藏结构与服务方式的变化,统一检索与资源发现,阅读推广与新媒体服务,24小时自助借还功能与流动书车,倡导提高阅读量。学习共享空间、双创发展空间应运而生。
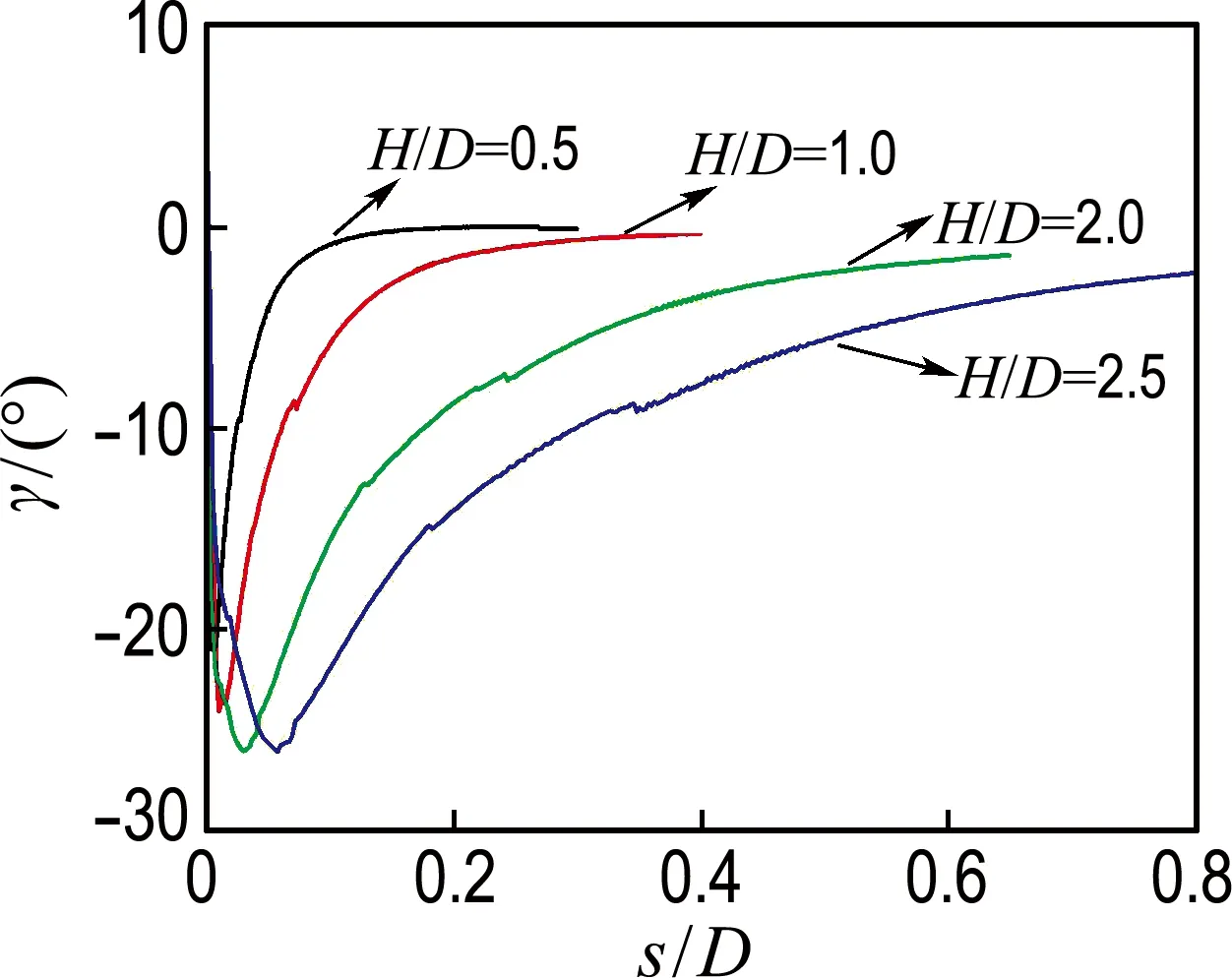
图3 吸力桶壁端部非共轴角度发展规律Fig.3 Development rules of non-coaxial angles atnthe bottoms of suction bucket walls
由图3可知:(1)在不同高径比条件下,非共轴角度的发展规律均相同:在地基变形初期,非共轴角度较大;随着变形的增加,非共轴角度逐渐趋近于零.(2)随着高径比的增加,非共轴角度达到零的速率逐渐减缓,表明非共轴现象愈趋明显.(3)在不同高径比条件下,非共轴角度在地基变形初期均有一个最小值,此时的非共轴现象最显著.例如:当H/D分别为0.5、1.0、2.0和2.5时,该最小值分别为-21o、-24o、-26o和-26o,表明当高径比超过2.0时,非共轴角度的最小值不再受到高径比变化的影响.(4)随着高径比的增加,非共轴角度达到最小值时(非共轴现象最显著),地基变形越来越大.
2.3.2 其他位置土体非共轴角度变化规律 针对桶体周围其他3个位置的土体,分析高径比与非共轴角度之间的对应关系,如图4所示.
土体对桶形基础的阻力作用主要集中在4个区域:桶壁端部、桶顶内侧、桶壁内侧和外侧,这4个区域内土体主应力方向的旋转规律如图1所示.图中,H、D、s分别为吸力桶基础高度、宽度、竖向位移,主应力方向α为土体单元最大主应力方向.
由图2可知:(1)主应力方向与塑性主应变增量方向的旋转变化是不完全一致的,非共轴角度在地基变形初期非常明显.随着地基变形的增加,非共轴角度逐渐减小.(2)主应力方向的发展速率明显滞后于塑性主应变增量方向的衰减速率.
2.4 桶形基础荷载-变形特性分析
2.4.1 竖向荷载-位移关系 以高径比H/D=0.5为例,分别采用传统共轴模型和所建立非共轴模型进行数值分析,研究桶形基础的竖向荷载-位移关系,如图5所示,其中,纵坐标为竖向荷载
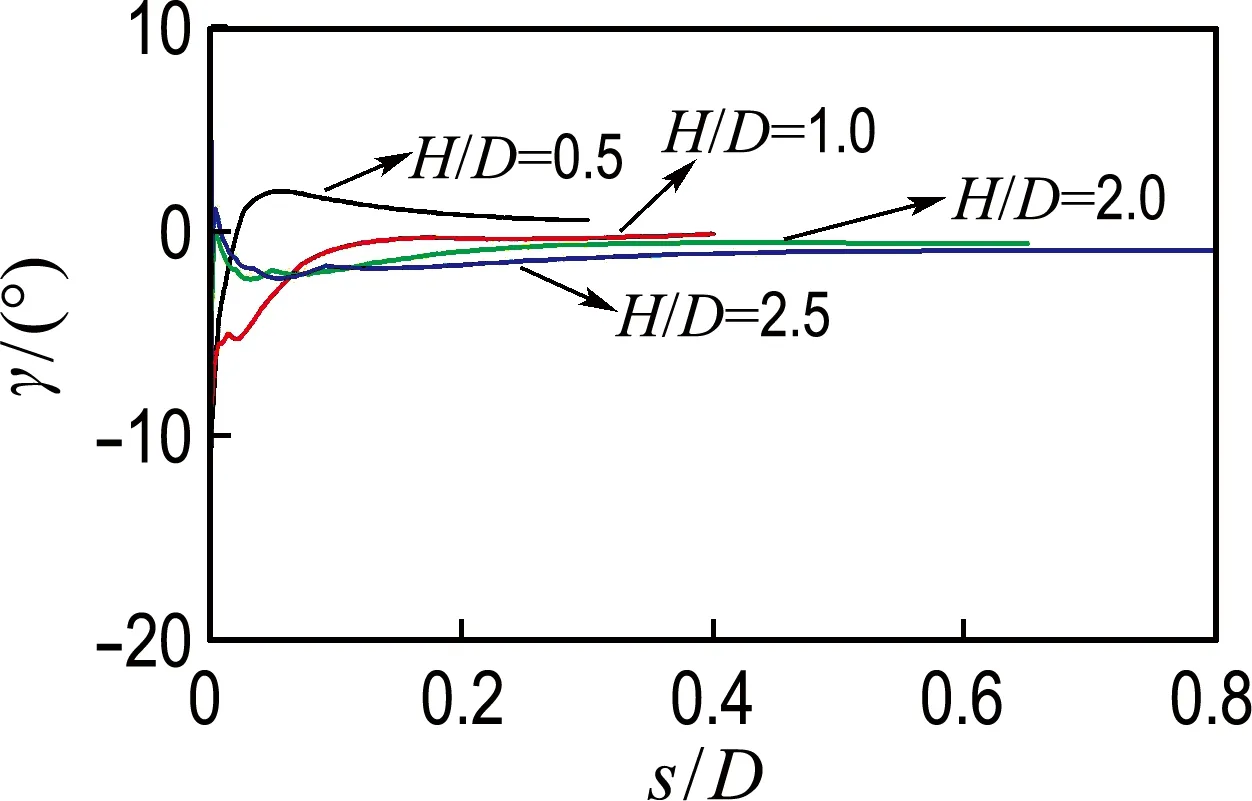
(a) 桶顶内侧
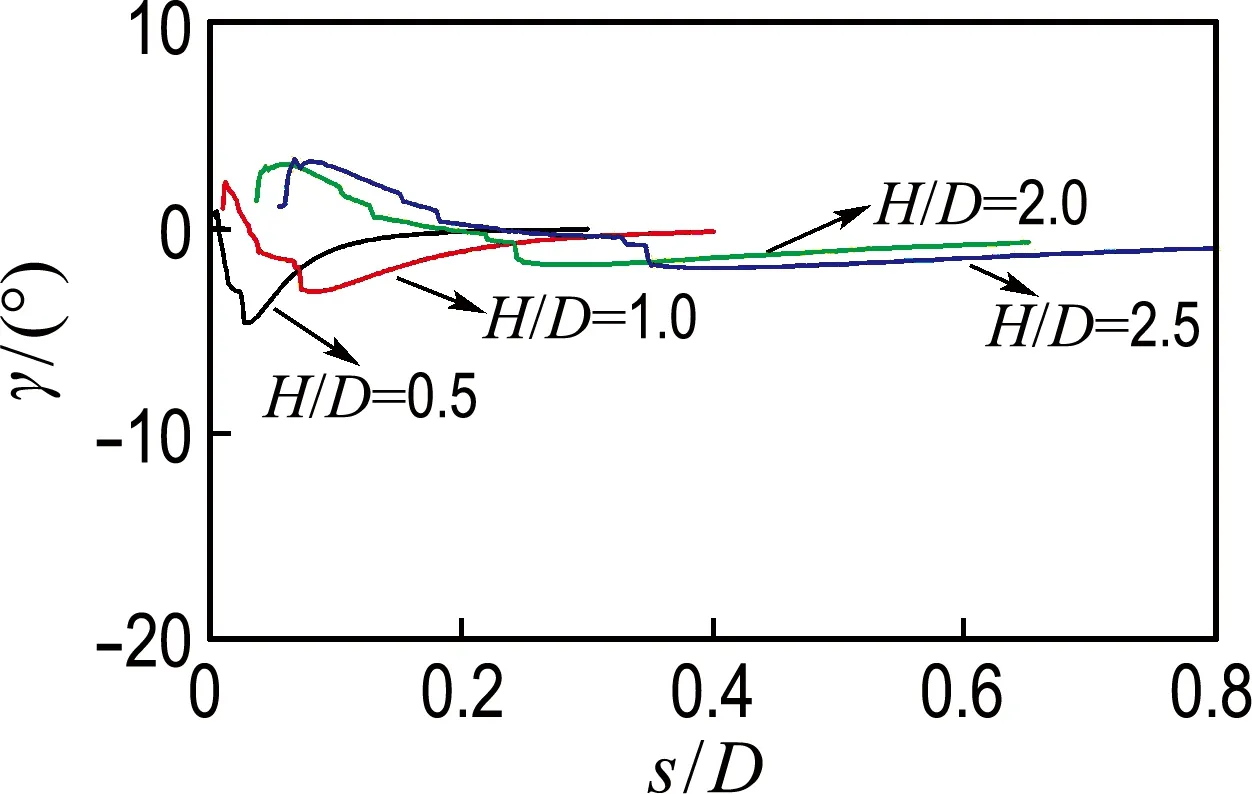
(b) 桶壁内
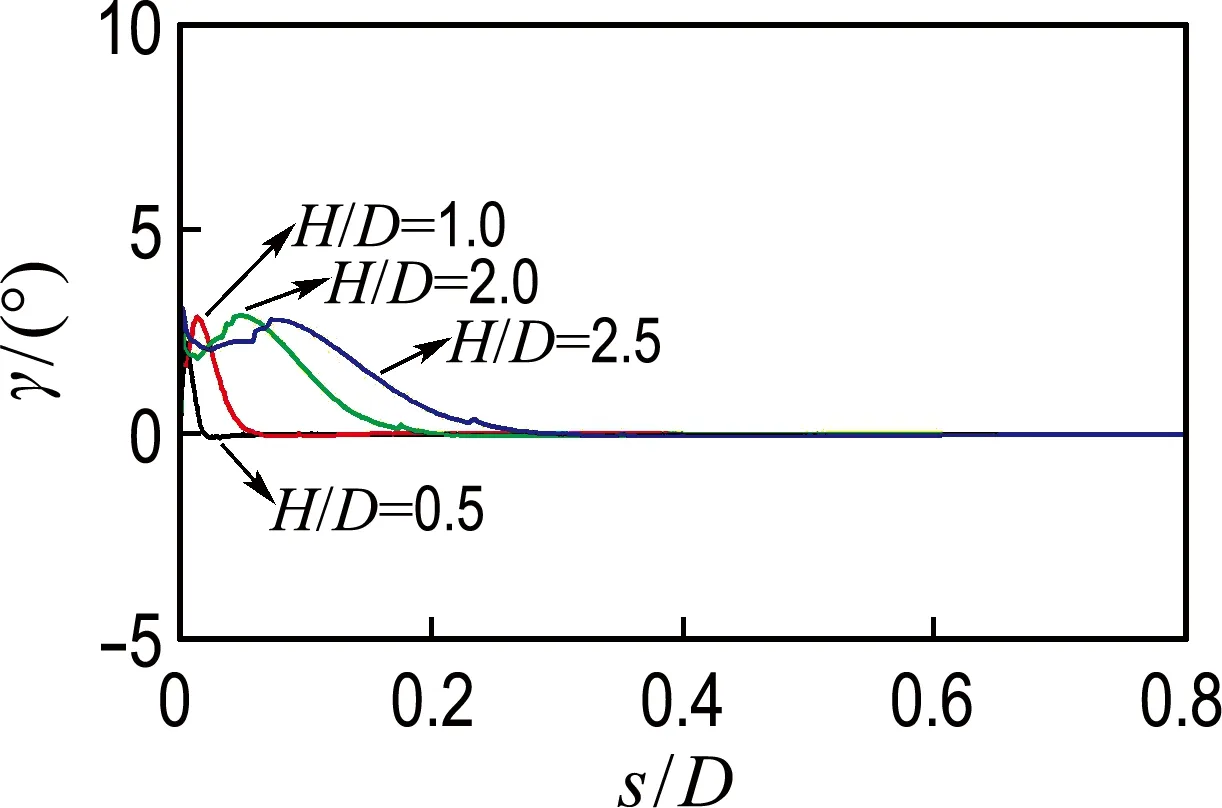
(c) 桶壁外侧
图4 土体非共轴角度发展规律
Fig.4 Development rules of non-coaxial angles of soi
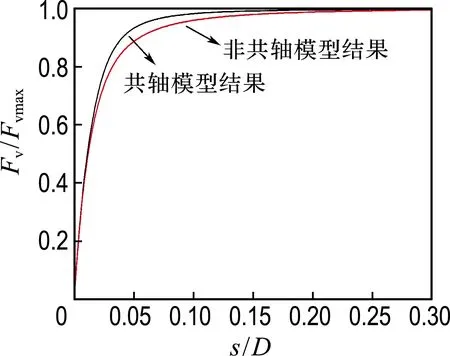
图5 桶形基础荷载-位移关系(H/D=0.5)Fig.5 Relations of load-displacement of bucketnfoundation with H/D=0.5
Fv与最大竖向荷载Fvmax的归一化值.
由图5可知:(1)在地基变形初期,地基处于弹性变形阶段,两种模型数值计算结果之间的差异可以忽略,表明非共轴特性对数值计算结果的影响可以不考虑.(2)在地基变形中期,地基处于弹塑性变形阶段,两种模型计算结果之间的差异比较显著,非共轴模型的计算结果的增长趋势滞后于共轴模型计算结果,表明:在相同竖向位移条件下,非共轴模型计算得到的竖向荷载低于共轴模型计算结果;在相同竖向荷载条件下,非共轴模型计算得到的地基变形大于共轴模型计算结果.(3)在地基变形后期,两种模型计算结果逐渐趋于一致,非共轴特性的影响逐渐减弱.
2.4.2 不同高径比条件下结果分析 在不同高径比条件下,分析共轴和非共轴模型计算结果之间的差异在地基变形过程中的变化规律,如图6所示.图中,纵坐标为非共轴和共轴模型计算得到的竖向荷载差异百分比ΔF.
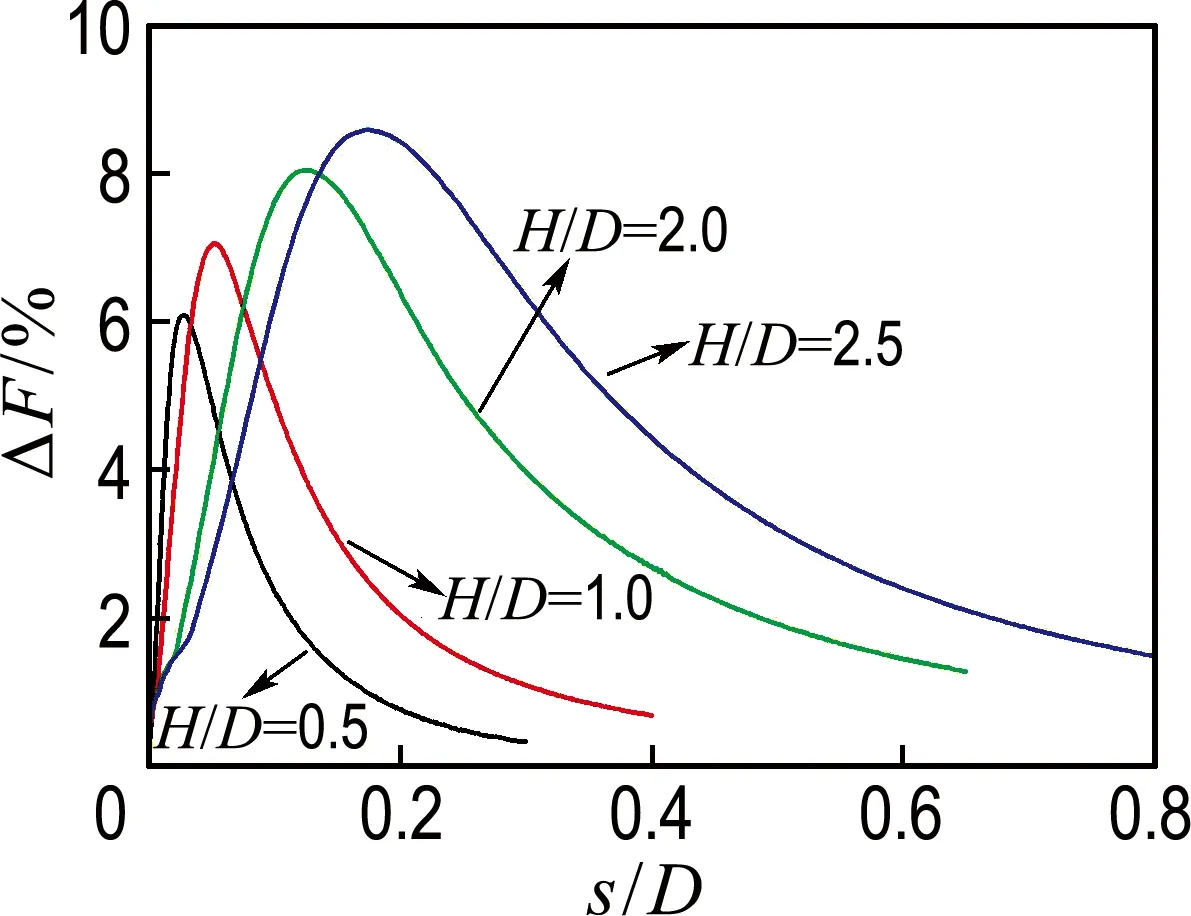
图6 桶形基础竖向荷载差异-位移关系Fig.6 Relations of vertical load-difference andndisplacement of bucket foundation
有限元模型采用轴对称单元进行数值积分.采用Dr=40%的饱和中密砂,浮容重为6 kN/m3,内摩擦角φ=30°,弹性模量E=50 MPa,泊松比υ=0.3.桶体直径D=4 m,壁厚0.02 m,采用刚体单元建立桶体模型.为了减少边界效应,模型水平方向长度取为10D,深度方向取为6D.
3 结 论
(1)在土体剪切变形过程中,主应力方向处于单调旋转状态.桶形基础高径比对土体主应力方向的旋转规律(方向、速率和极值)有显著影响.
9.1.3斑潜蝇 是20世纪90年代初转入我国的多食性害虫,一年发生7~8代,以各种虫态在温室内越冬。成虫有趋黄性,雌成虫刺伤叶片,将卵产入其中,幼虫蛀食叶时形成曲折隧道,影响光合作用,降低产量。
应变增量与应力增量的关系如下:
由图1可知:(1)在竖向荷载作用过程中,土体主应力方向处于旋转状态.由初始值(对应于土体自重)逐渐向极值(对应于竖向极限荷载)发展.达到极值后,主应力方向处于稳定状态.(2)主应力方向的旋转变化是单调的,例如:在桶壁端部和桶壁内侧,主应力方向呈顺时针旋转(数值为负);然而,桶顶内侧和桶壁外侧土体的主应力方向呈逆时针旋转(数值为正).(3)高径比的变化对主应力方向的极值有显著影响.在图1(a)中,当高径比为0.5、1.0和2.0时,极值分别为-23°、-21°和-20°,表明主应力方向的极值随着高径比的增加而增加.然而,当高径比为2.5和2.0时,两者的主应力方向极值非常接近,表明高径比变化对极值的影响在高径比超过2.0时可以忽略.同理,在图1(b)、(c)、(d)中可得到同样结论.(4)在桶壁端部、内侧和外侧,随着高径比的增加,主应力方向达到极值的发展速率逐渐减小.然而,在桶顶内侧,主应力方向在变形初期即达到极值,可以忽略高径比对其发展速率的影响.
(4)当地基处于弹塑性变形阶段,非共轴特性对荷载-位移关系的发展趋势有显著的减缓作用;在其他地基变形阶段,非共轴特性的影响比较微弱.
美国政府曾多次强调不给任何国家和任何公司制裁豁免,并要求所有国家在“过渡期”后同伊朗的原油交易清零,但遭到很多同伊朗有大宗原油贸易国家的强烈反对。2018年11月5日,特朗普政府宣布给予中国、印度、意大利、希腊、日本、韩国、土耳其和中国台湾地区“重大削减例外”的豁免,理由是这些国家和地区已大幅减少对伊朗石油的购买[20]。美国制裁政策规定了特殊情况下的例外情况。
(5)随着高径比的增加,非共轴特性对地基竖向荷载-位移关系的影响逐渐增加.
[1]武 科,栾茂田,范庆来,等. 桶形基础承载性能的弹塑性有限元数值分析[J]. 大连理工大学学报, 2008, 48(5):702-707.
WU Ke, LUAN Maotian, FAN Qinglai,etal. Numerical analysis of bearing capacity behavior of bucket foundation based on elasto-plastic FEM [J]. Journal of Dalian University of Technology, 2008, 48(5):702-707. (in Chinese)
[2]张 宇,王 梅,楼志刚. 竖向载荷作用下桶形基础与土相互作用机理研究[J]. 土木工程学报, 2005, 38(2):97-101.
ZHANG Yu, WANG Mei, LOU Zhigang. A study on the mechanism of interaction between bucket foundation and soil under vertical loadings [J]. China Civil Engineering Journal, 2005, 38(2):97-101. (in Chinese)
楚墨很早就注意到静秋。他走过学校的林荫道,一棵古老的银杏树下面,静秋手捧一本书,安静地坐在那里。夕阳为她镀上一圈金黄色的美丽轮廓,静秋就像一个降临世间的女神。楚墨经过她的身边,女神抬头看她,笑笑,又低下头,翻一页书。一片银杏叶飘落下来,全世界的花儿在那一刻,齐刷刷地开放。
[3]武 科,栾茂田,范庆来,等. 滩海桶形基础破坏机制及极限承载力分析研究[J]. 岩土工程学报, 2008, 30(3):394-398.
WU Ke, LUAN Maotian, FAN Qinglai,etal. Failure mechanism and ultimate bearing capacity of bucket foundation in shallow water [J]. Chinese Journal of Geotechnical Engineering, 2008, 30(3):394-398. (in Chinese)
[4]鲁晓兵,矫滨田,刘 亮. 饱和砂土中桶形基础承载力的实验研究[J]. 岩土工程技术, 2006, 20(4):170-172.
LU Xiaobing, JIAO Bintian, LIU Liang. Experimental study on the bearing capacity of bucket foundation in saturated sand [J]. Geotechnical Engineering Technique, 2006, 20(4):170-172. (in Chinese)
[5]BRANSBY M F, RANDOLPH M F. Combined loading of skirted foundations [J]. Géotechnique, 1998, 48(5):637-655.
[6]GOURVENEC S, RANDOLPH M. Effect of strength non-homogeneity on the shape of failure envelopes for combined loading of strip and circular foundations on clay [J]. Géotechnique, 2003, 53(6):575-586.
[7]MADSEN O S. Wave-induced pore pressures and effective stresses in a porous bed [J]. Géotechnique, 1978, 28(4):377-393.
[8]ISHIHARA K, TOWHATA I. Sand response to cyclic rotation of principal stress directions as induced by wave loads [J]. Soils and Foundations, JSSMFE, 1983, 23(4):11-26.
[9]沈瑞福,王洪瑾,周克骥,等. 动主应力旋转下砂土孔隙水压力发展及海床稳定性判断[J]. 岩土工程学报, 1994, 16(3):70-78.
SHEN Ruifu, WANG Hongjin, ZHOU Keji,etal. Building-up of pore water pressure under cyclic rotation of principal stress and evaluation of stability of seabed deposit [J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3):70-78. (in Chinese)
[10]姚仰平,谢定义. 砂土的形变能破坏准则[J]. 西安理工大学学报, 1994, 10(1):42-46.
YAO Yangping, XIE Dingyi. Criterion for the destructiveness of sand deformation energy [J]. Journal of Xi′an University of Technology, 1994, 10(1):42-46. (in Chinese)
[11]ROSCOE K H. The influence of strains in soil mechanics [J]. Géotechnique, 1970, 20(2):129-170.[12]JOER H A, LANIER J, FAHEY M. Deformation of granular material due to rotation of principal axes [J]. Géotechnique, 1998, 48(5):605-619.
[13]YANG Yunming, YU Haisui. Numerical simulations of simple shear with non-coaxial models [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(1):1-19.
[14]YANG Yunming, YU Haisui. Application of a non-coaxial soil model in shallow foundations [J]. Geomechanics and Geoengineering:an International Journal, 2006, 1(2):139-150.
[15]RUDNICKI J W, RICE J R. Conditions for the localization of deformation in pressure-sensitive dilatant materials [J]. Journal of the Mechanics and Physics of Solids, 1975, 23(6):371-394.
[16]罗 强. 非共轴本构模型的数值应用及离心机试验研究[D]. 大连:大连理工大学, 2013.
LUO Qiang. Numerical application and centrifugal modeling study of a non-coaxial constitutive model [D]. Dalian:Dalian University of Technology, 2013. (in Chinese)
Research on vertical load-deformation behavior of suction bucket foundations in consideration of non-coaxial characteristic
LUO Qiang*1,FENG Na2,JIA Hu1
(1.Academy of Civil Engineering and Architecture, Nanyang Normal University, Nanyang 473061, China;2.Institute of Economics and Management, Henan Polytechnic Institute, Nanyang 473000, China )
The directions of principal stress could rotate during the shearing process of soils, meanwhile, the difference between the directions of the principal stress and the plastic principal strain increment is obvious, which is called the non-coaxial phenomenon. In view of the suction buckets foundations, a non-coaxial constitutive model of soil is used to analyze the change rules of the rotations of the directions of the principal stress and the non-coaxial angles, and to study the non-coaxial influence to the relations of the load and the displacement of the foundation. The study results show that the directions of the principal stress rotate monotonously in the vertical loading process, and that the height-diameter ratio of the suction bucket foundations has obvious influence to the rotations rule of the principal stress directions at the aspects of the direction, speed and extreme value. The non-coaxial characteristic could slow down the development trend of the relations of the load and displacement, which is more obvious at the middle of the deformation process of the foundation. When the height-diameter ratio increases, the non-coaxial characteristic is more obvious and its influence to the vertical loading-displacement relations of the foundation is also more obvious.
non-coaxial theory; principal stress direction; suction bucket; constitutive model; numerical analysis
1000-8608(2017)04-0390-06
2017-02-10;
2017-05-28.
国家自然科学基金资助项目(51609117,51209028);河南省教育厅科学技术研究重点项目(14B560023).
罗 强*(1981-),男,博士,讲师,E-mail:luoqiang1212@sina.com.
TU473.1
A
10.7511/dllgxb201704009

