双列深沟球轴承刚柔耦合多体接触建模与振动特性研究
蒋 玲 莉,卜 忠 颉,韩 清 凯,2,李 学 军
(1.湖南科技大学 机械设备健康维护省重点实验室, 湖南 湘潭 411201;2.大连理工大学 机械工程学院, 辽宁 大连 116024 )
双列深沟球轴承刚柔耦合多体接触建模与振动特性研究
蒋 玲 莉*1,2,卜 忠 颉1,韩 清 凯1,2,李 学 军1
(1.湖南科技大学 机械设备健康维护省重点实验室, 湖南 湘潭 411201;2.大连理工大学 机械工程学院, 辽宁 大连 116024 )
在研究双列深沟球轴承各组件之间动力学关系的基础上,基于弹性流体动力润滑理论和赫兹接触理论,利用多体动力学分析软件ADAMS,结合有限元分析软件ANSYS柔性化处理,建立了双列深沟球轴承刚柔耦合多体接触动力学仿真模型.综合赫兹接触刚度和润滑接触刚度的影响得到双列深沟球轴承等效刚度.分析了不同荷载、转速、油膜厚度对双列深沟球轴承振动特性的影响,结果表明,合适的荷载可抑制双列深沟球轴承振动;转速的增加可加剧振动;随着油膜厚度的增大,振动先减小后增大.研究结果为双列深沟球轴承结构优化设计、减振降噪和运行状态监测提供了参考依据.
双列深沟球轴承;刚柔耦合;弹性流体动力润滑;接触刚度;振动特性
0 引 言
滚动轴承是机械设备的重要基础零件,其振动特性直接影响整机的性能与使用寿命.机械设备高可靠性和高精度趋势的发展,对轴承的振动特性提出了愈来愈高的要求,轴承的振动特性已成为机械行业研究的热点内容之一.双列深沟球轴承是机械行业中使用广泛的一类滚动轴承,相较于单列深沟球轴承,其不仅可承受更高径向负荷,还可以承受作用在两个方向的轴向负荷,在航空航天、矿山、冶金和重型机械行业有着广泛应用.开展双列深沟球轴承振动特性研究,对双列深沟球轴承结构优化设计、减振降噪和运行状态监测均可提供参考依据,具有重要意义.
国内外已有部分学者开展了深沟球轴承的动力学建模与动态特性分析,文献[1-3]对角接触轴承的刚度进行了部分研究,分析了其动刚度特性;文献[4]利用显式动力学理论进行了滚动轴承动力学仿真分析;文献[5-7]进行了滚动轴承的动态仿真和动态特性的分析;文献[8]建立了滚动轴承的弹性接触振动模型,探讨了滚动轴承振动的本质.在以往大多数的研究中存在如下不足:忽略了油膜厚度对轴承接触刚度的影响,将赫兹接触刚度近似地看成轴承的刚度;忽略了轴承套圈的柔性体特征,无法真实反映滚动体和套圈之间的接触力;以单列深沟球轴承为对象,对双列深沟球轴承的振动特性研究较少.
基于此,本文以双列深沟球轴承4205为研究对象,综合赫兹接触刚度和润滑接触刚度对轴承等效刚度的影响,将内外圈柔性化处理后,建立其刚柔耦合多体接触动力学模型,研究双列深沟球轴承在不同荷载、转速及油膜厚度下的振动特性.
1 多体接触模型及其等效刚度
双列深沟球轴承结构简图如图1所示,滚动轴承受载接触时,滚动体与套圈之间将发生非线性弹性变形[9].而滚动体与套圈之间的接触荷载和接触变形是研究其振动特性的关键因素.在ADAMS动力学仿真时,滚珠与内外圈接触刚度的设置尤为重要,如果接触刚度设置不合理,将直接影响接触碰撞模型接触力计算结果的准确性,从而影响轴承振动特性分析结果的正确性,导致仿真失败.本文结合弹性流体动力润滑理论和赫兹接触理论,计算等效刚度,作为滚珠和内外圈之间的接触刚度.

图1 双列深沟球轴承结构简图Fig.1 The structure diagram of double-row deep- groove ball bearing
1.1 赫兹接触刚度
滚动轴承依靠滚道和滚动体的相互接触来支承荷载[10],赫兹接触理论根据完全弹性的静态接触条件得出,滚动轴承的接触问题符合赫兹接触理论.根据赫兹接触理论,滚动体与滚道接触面是一个椭圆,如图2所示.

图2 钢球与滚道的接触形态Fig.2 The contact form between steel ball and raceway
简化解求得接触面的形变量为
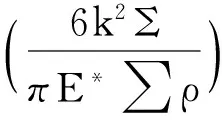
(1)
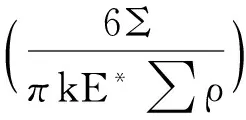
(2)
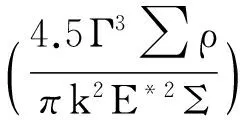
(3)
式中:a为椭圆接触面的长半轴半径;b为短半轴半径;Q为接触荷载;δ为最大弹性变化量;∑ρ为曲率和;Γ、Σ分别为第一类和第二类全椭圆积分;k为椭圆率;E*为等效弹性模量.
滚动轴承刚度是指轴承套圈在负荷方向上产生单位相对弹性位移量所需的外加负荷[11],可表示为

(4)
由式(3)变形得到滚动体与滚道接触时所产生的接触荷载为
(5)
式中:Ki(o)为滚动体与滚道接触处的荷载变形系数[12];δi(o)为滚动体与滚道的弹性变形;下标i、o分别表示内、外圈.
联合式(4)、(5)得滚动体与滚道的赫兹接触刚度为
(6)
1.2 润滑接触刚度
轴承在运转过程中,滚动体和滚道接触时会形成弹性流体润滑油膜[13].润滑影响钢球与滚道摩擦副的接触特性,进而影响轴承的振动特性,弹性流体动力润滑接触模型如图3所示.
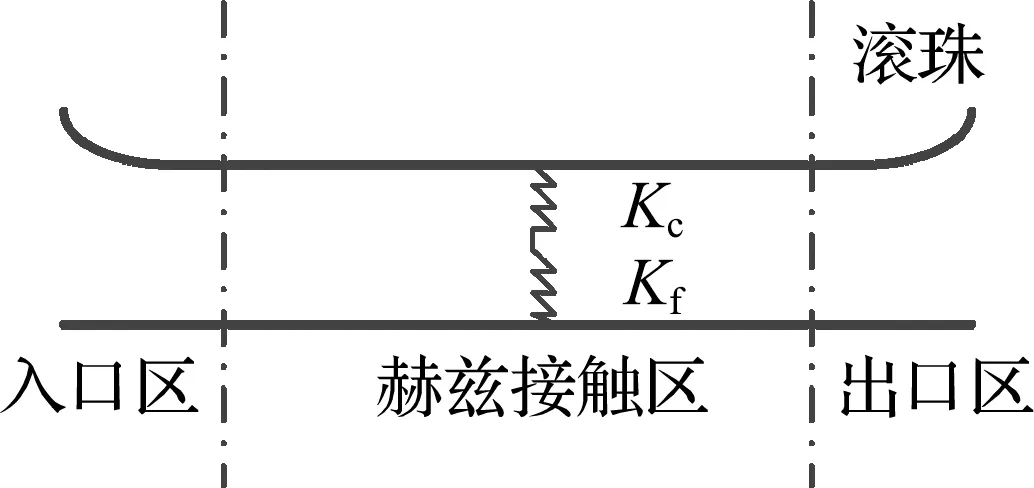
图3 弹性流体动力润滑接触模型Fig.3 The contact model of elastohydrodynamic lubrication
根据弹性流体动力润滑理论,最小油膜厚度决定了滚动轴承的油膜刚度.在等温且充足供油条件下,滚动体与套圈之间量纲一最小油膜厚度为[14]
Hmin=3.63U0.68G0.49W-0.073(1-e-0.68k)
(7)
滚动体与套圈之间的油膜厚度为
hmin=HminRx
(8)
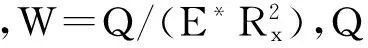
根据式(7)和(8)即可得到滚动体与套圈之间的油膜刚度为

(9)
1.3 等效刚度
滚动轴承赫兹接触刚度和油膜刚度串联的钢球-滚道等效刚度计算模型如图4所示.通过式(6)和(9)得到的赫兹接触刚度和油膜刚度,计算滚道和滚动体之间的等效刚度为
(10)

图4 滚动体-滚道接触副等效刚度计算模型Fig.4 The equivalent rigidity calculation model of contact pair between ball and raceway
2 刚柔耦合多体接触动力学模型
本文以双列深沟球轴承4205为研究对象,其基本结构参数见表1.计算所用到的润滑油主要参数见表2.
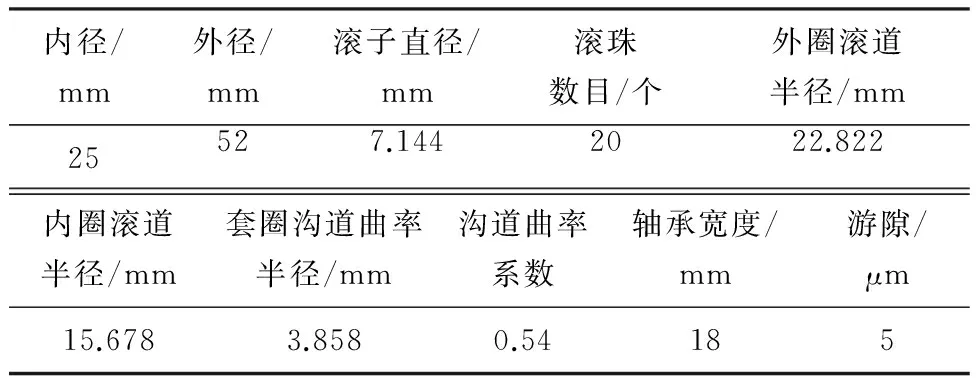
表1 轴承结构参数Tab.1 The structure parameters of bearing

表2 润滑油主要参数Tab.2 The main parameters of lubricating oil
运用CATIA软件对双列深沟球轴承进行三维建模,然后利用接口软件SimDesigner导入ADAMS.ADAMS中默认的是全刚性体动力学分析,仿真分析时不考虑物体的小变形.如果把套圈当成理想的刚性体,则无法准确体现滚动体与套圈接触微小区域的弹性接触变形,从而无法真实有效地反映轴承的振动特性.而滚动体与套圈的弹性接触面积是影响其接触力和摩擦力的重要因素;元件之间的接触力主要依靠套圈的形变传递[15];把双列深沟球轴承套圈设置为柔性体仿真时,能准确地还原其运动过程中滚动体和内外圈之间的相互作用力和弹性变形,进而准确地还原其振动特性.
本文利用有限元分析软件ANSYS对双列深沟球轴承的内外圈进行模态分析,生成模态中性文件,在ADAMS中替换刚性的内外圈.采用ADAMS中的Impact接触力函数,定义了滚动体与套圈、保持架兜孔,保持架与套圈之间的接触关系.其广义形式表现为
(11)
其中采用了step函数,qo为两物体的初始距离,q为两物体实际距离,dq/dt为两物体之间的距离随时间的变化率;e为力指数,由赫兹接触理论可取1.5;cmax为最大阻尼系数,s为切入深度,根据文献[16]所述,可分别取10和0.1;K为接触刚度,由赫兹接触理论得出.
通过接触的定义,利用虚拟样机技术建立了基于内外圈柔性体的双列深沟球轴承刚柔耦合多体接触动力学模型,如图5所示.

图5 双列深沟球轴承ADAMS仿真模型Fig.5 The ADAMS simulation model of double-row deep-groove ball bearing
3 双列深沟球轴承振动特性分析
3.1 模型对比验证
3.1.1 运动学特性分析 根据轴承各部件运动学关系,可以得到轴承零件之间的运动特性.由文献[10]可知:当滚珠与滚道为纯滚动时,可以推算出滚动体公转线速度、滚动体自转速度、保持架旋转速度等运动学参数.在转速为2 400 r/min时,仿真值与计算结果的对比如表3所示.
由表3可知,保持架旋转速度、滚珠公转线速度、滚球自转速度的误差分别为1.70%、1.97%、6.26%.所建模型的运动学仿真结果与理论计算误差较小,模型满足运动学特性.
3.1.2 频谱特性分析 采用ADAMS进行多体动力学仿真,提取双列深沟球轴承的振动加速度信号,进行频谱特性分析.

表3 运动学参数仿真与计算值对比Tab.3 Simulation and calculation comparison of kinematic parameters
图6~8为双列深沟球轴承滚动体加速度的时域信号图和频域信号图.其中x、z向为径向,y向为轴向.由图可知,径向的时频信号基本一致,且比轴向的振动大,主要特征频率为16.23 Hz,与保持架旋转频率一致,轴向频谱无明显特征频率,这与文献[17]的分析结果一致.
刚柔耦合双列深沟球轴承运动学仿真与频谱特性分析验证了模型的正确性.

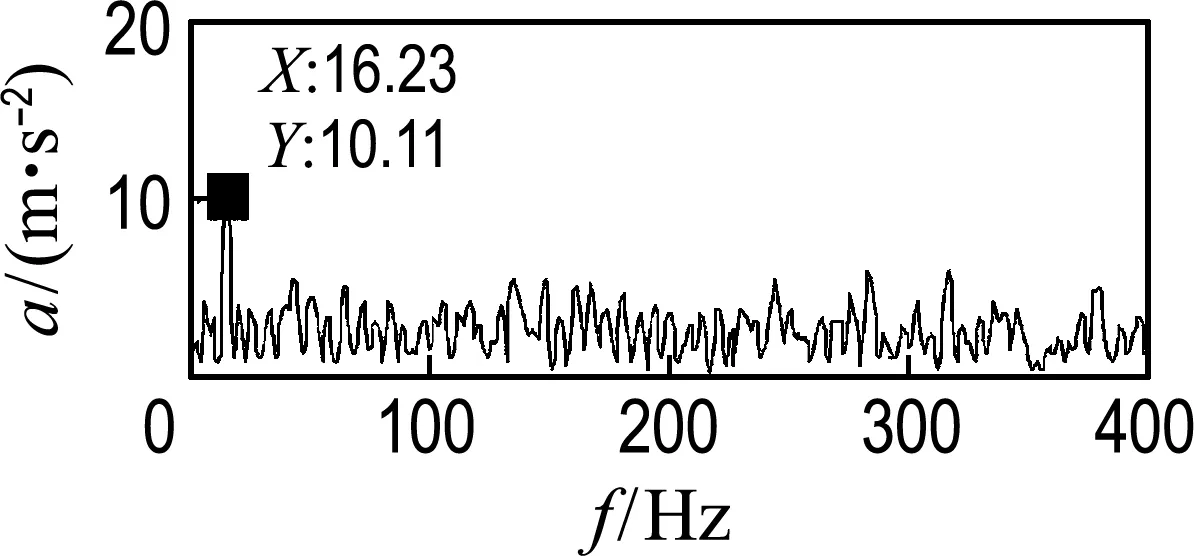
(a) 时域信号(b) 频域信号
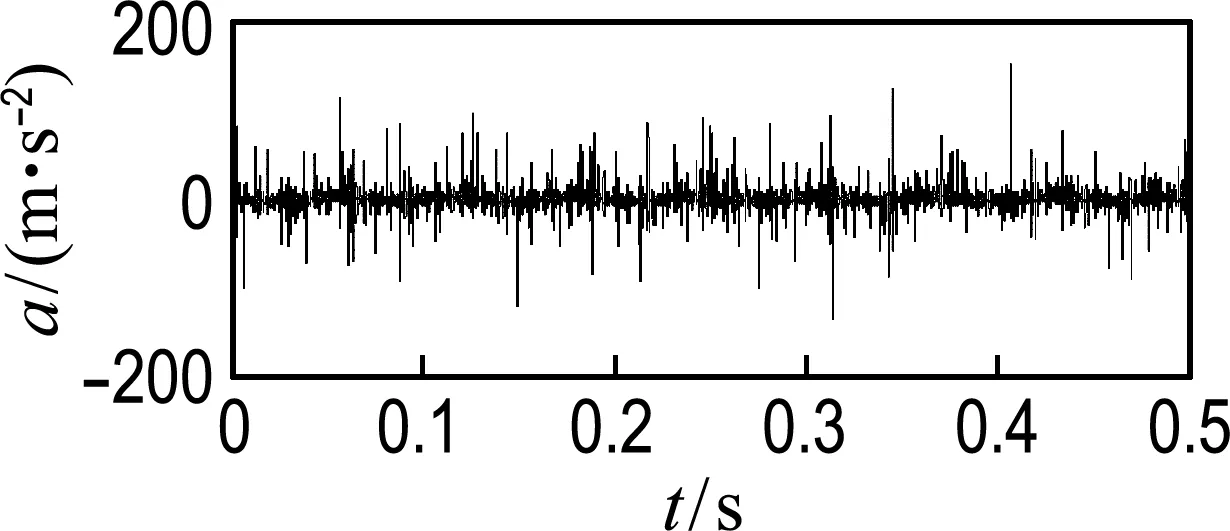
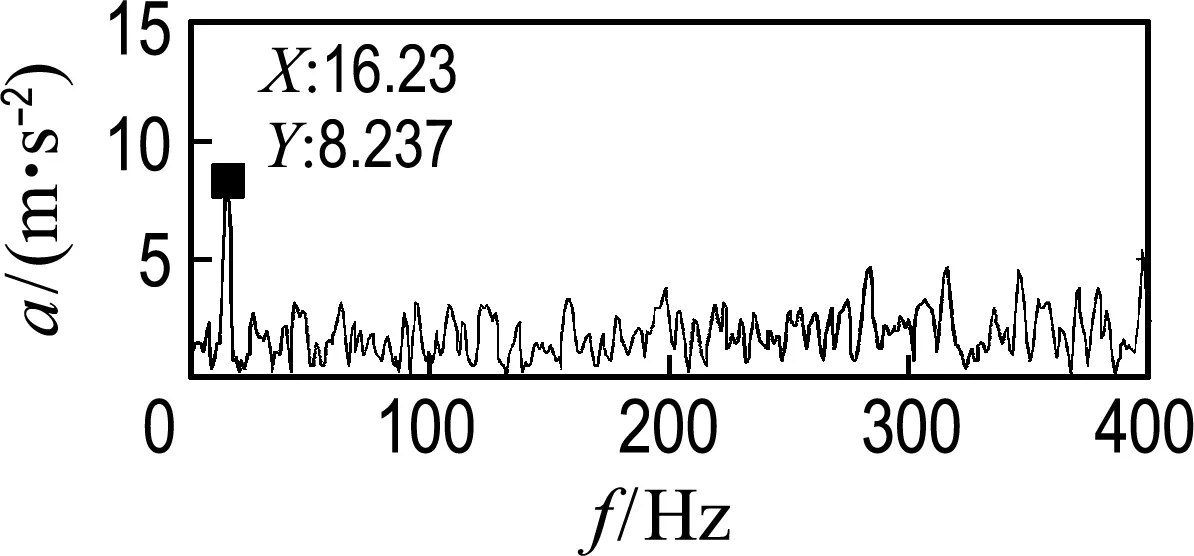
(a) 时域信号(b) 频域信号

(a) 时域信号

(b) 频域信号
图8 滚动体y方向加速度
Fig.8 Acceleration of rolling body iny-direction
3.2 荷载对轴承振动的影响分析
双列深沟球轴承在承受的荷载发生变化时,会引起滚动体与套圈之间的接触荷载改变,使得滚动轴承的接触刚度产生相应的改变.而接触刚度的改变使接触副的接触特性产生了变化,影响轴承的振动特性.根据上述等效刚度计算理论,得到不同荷载作用下的等效刚度,如图9所示.由图可知,随着接触荷载的增大,内外圈与滚珠之间的等效刚度增大;内圈与滚珠的等效刚度小于外圈与滚珠的等效刚度,且随着接触荷载的增大,二者的差值增大.

图9 接触荷载对等效刚度的影响Fig.9 The effect of contact load on equivalent stiffness
本文在ADAMS中对双列深沟球轴承在不同荷载下的振动特性进行了仿真分析.
3.2.1 径向荷载对轴承振动的影响 内圈转速为600 r/min时,分别施以纯径向荷载以及联合施加200、300、400 N轴向荷载,轴承振动与荷载的关系如图10所示,图中Fa表征联合施加的轴向荷载值,纵坐标L表示轴承的振动加速度级.随着径向荷载的增大振动值增大,当径向荷载较小时,联合施加的轴向荷载增大将加剧振动;随着径向荷载的增大,联合施加的轴向荷载反而可在一定程度上抑制振动.本文分析案例中当径向荷载大于1 000 N时,联合施加的轴向荷载对振动有一定的抑制作用.
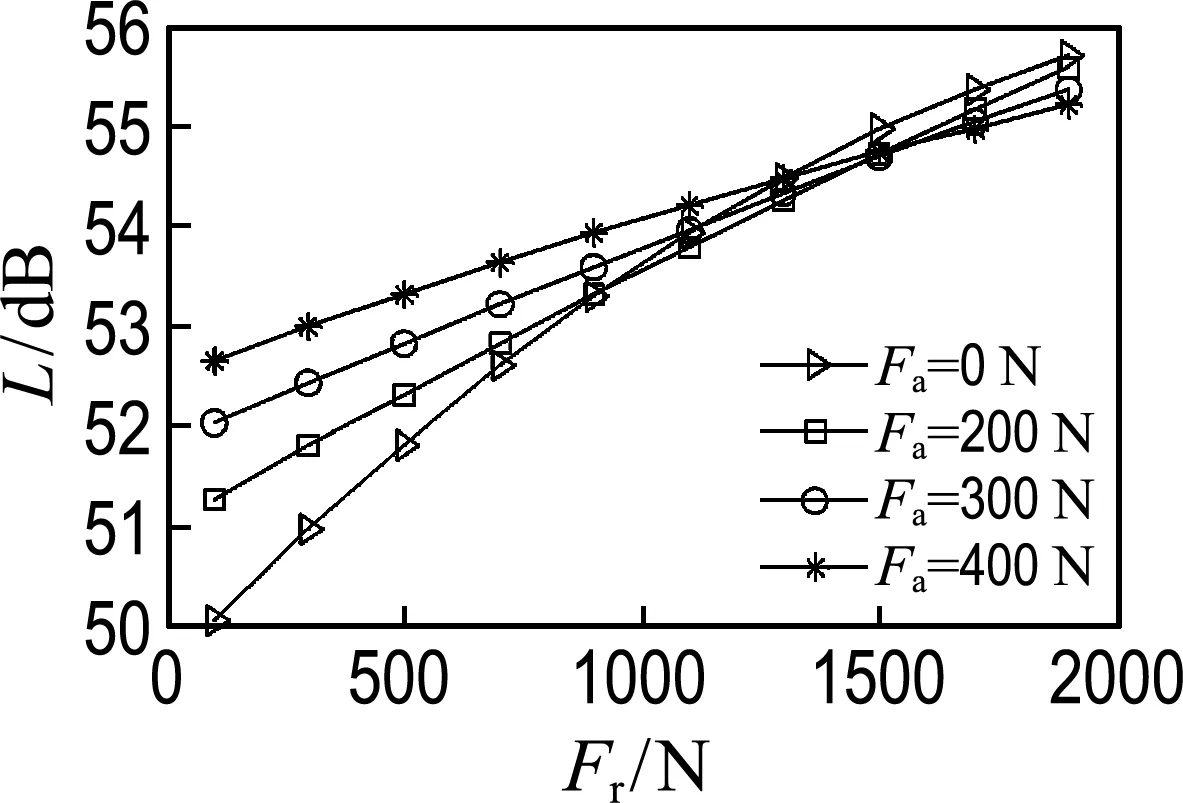
图10 径向荷载与轴承振动的关系Fig.10 The relationship between radial load andnbearing vibration
3.2.2 轴向荷载对轴承振动的影响 内圈转速为600 r/min时,分别施以纯轴向荷载以及联合施加300、500、1 000 N径向荷载,轴承振动与荷载的关系如图11所示,图中Fr表征联合施加的径向荷载值,横坐标μ表示轴向荷载与额定动荷载的比值,纵坐标L表示轴承的振动加速度级.当轴向荷载较小时,联合施加的径向荷载增大将加剧振动;随着轴向荷载的增大,联合施加的径向荷载反而可在一定程度上抑制振动.说明合适的轴向与径向荷载共同作用对双列深沟球轴承的振动均有抑制作用.

图11 轴向荷载与轴承振动的关系Fig.11 The relationship between axial load andnbearing vibration
3.3 转速对轴承振动的影响分析
轴承的转速影响滚动体与内外圈接触副中润滑油膜的形成,导致油膜刚度产生变化.随着转速的增大,滚珠与套圈之间的油膜刚度减小,等效刚度的变化主要来源于油膜刚度的变化,这是由转速增大,滚珠和套圈之间的润滑油流速增大造成的.根据上述等效刚度计算理论,可以得到转速对等效刚度的影响,如图12所示.

图12 转速对等效刚度的影响Fig.12 The effect of rotational speed on equivalentnstiffness
径向荷载和轴向荷载同时为500 N时,内圈转速与轴承振动关系如图13所示,纵坐标L表示轴承的振动加速度级.随着内圈转速的增大,轴承振动呈近似线性增大.
3.4 油膜厚度对轴承振动的影响分析
油膜的形成对双列深沟球轴承振动特性的影响很大,合理控制油膜的厚度是抑制轴承振动的关键.当润滑油参数及种类不同时,由式(7)和(8)可知,在相同的转速以及荷载的情况下,滚动体与套圈之间形成的油膜厚度不一样.通过选取不同油膜厚度,分析了油膜厚度对等效刚度的影响,得到了图14油膜厚度与等效刚度的关系曲线.图15为内圈转速600 r/min、轴向荷载和径向荷载为500 N时,油膜厚度与轴承振动的关系,纵坐标L表示轴承的振动加速度级.由图可知,随着油膜厚度的增大,轴承振动先减小后增大.油膜越薄时,油膜刚度越大,滚珠与套圈之间的受力区域变小,振动值增大;油膜越厚,油膜刚度越小,受力区域不稳定,振动值增大.因此轴承润滑时,根据工况条件要合理控制油膜厚度,合理选取润滑液.

图15 油膜厚度与轴承振动的关系Fig.15 The relationship between oil film thickness andnbearing vibration
4 结 论
(1)综合考虑赫兹接触刚度和润滑接触刚度的刚柔耦合多体接触双列深沟球轴承模型,其运动学及振动时频域特性仿真与理论分析一致,可用于振动特性研究.
(2)合适的轴向与径向荷载共同作用对双列深沟球轴承的轴向振动和径向振动均有抑制作用.
(3)随着转速的增加,双列深沟球轴承振动加剧,呈近似线性关系.
(4)随着油膜厚度的增大,双列深沟球轴承振动先减小后增大.
(5)本文研究所得的双列深沟球轴承振动与荷载、转速、油膜厚度的关系曲线可作为其结构优化设计、减振降噪和运行状态监测的参考依据.
[1]吴明星,吴 维,胡纪滨,等. 考虑自旋的高速角接触球轴承油膜刚度计算[J]. 振动与冲击, 2014, 33(10):38-42.
WU Mingxing, WU Wei, HU Jibin,etal. Oil film stiffness calculation of high speed angular contact ball bearings considering spinning [J]. Journal of Vibration and Shock, 2014, 33(10):38-42. (in Chinese)
[2]GUNDUZ A, SINGH R. Stiffness matrix formulation for double row angular contact ball bearings:Analytical development and validation [J]. Journal of Sound and Vibration, 2013, 332(22):5898-5916.
[3]邓四二,董 晓,崔永存,等. 双列角接触球轴承动刚度特性分析[J]. 兵工学报, 2015, 36(6):1140-1146.DENG Si′er, DONG Xiao, CUI Yongcun,etal. Analysis of dynamic stiffness characteristics of double-row angular contact ball bearings [J]. Acta Armamentarii, 2015, 36(6):1140-1146. (in Chinese)
[4]张 刚,何永慧,张义民. 滚动轴承的多体接触动力学仿真[J]. 振动、测试与诊断, 2013, 33(s1):28-31.ZHANG Gang, HE Yonghui, ZHANG Yimin. Multi-body contact dynamics simulation of rolling bearing [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(s1):28-31. (in Chinese)
[5]朱利军,谭 晶,黄迪山,等. 基于ADAMS的深沟球轴承仿真分析[J]. 轴承, 2011, 2(2):3-6.
ZHU Lijun, TAN Jing, HUANG Dishan,etal. Simulation analysis of deep groove ball bearings based on ADAMS [J]. Bearing, 2011, 2(2):3-6. (in Chinese)
[6]李 昌,孙志礼. 基于弹流润滑理论的深沟球轴承动态虚拟仿真[J]. 航空动力学报, 2009, 24(4):951-956.
LI Chang, SUN Zhili. Dynamic virtual simulation of deep groove ball bearing:based on elastohydrodynamic lubrication theory [J]. Journal of Aerospace Power, 2009, 24(4):951-956. (in Chinese)
[7]张 利,黄少成,徐 娟,等. 基于弹流润滑理论的高速轴承动力学仿真分析[J]. 合肥工业大学学报(自然科学版), 2014, 37(5):516-519.
ZHANG Li, HUANG Shaocheng, XU Juan,etal. Dynamics simulation analysis of high-speed bearing based on elastohydrodynamic lubrication theory [J]. Journal of Hefei University of Technology (Natural Science), 2014, 37(5):516-519. (in Chinese)
[8]赵联春, 马家驹. 球轴承的弹性接触振动 [J]. 机械工程学报, 2003, 39(5):60-64.
ZHAO Lianchun, MA Jiaju. Elastic contact vibrations of ball bearings [J]. Chinese Journal of Mechanical Engineering, 2003, 39(5):60-64. (in Chinese)
[9]袁 幸,朱永生,张优云,等. 基于模型辨识的滚动轴承故障诊断[J]. 振动、测试与诊断, 2013, 33(1):12-17.
YUAN Xing, ZHU Yongsheng, ZHANG Youyun,etal. Rolling element bearings fault diagnosis based on physical model identification [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(1):12-17. (in Chinese)
[10]冈本纯三. 球轴承的设计计算[M]. 黄志强,译. 北京:机械工业出版社, 2003.
OKAMOTO J. Design Calculation of Ball Bearing [M]. HUANG Zhiqiang, trans. Beijing:China Machine Press, 2003. (in Chinese)
[11]HARRIS T A. Rolling Bearing Analysis [M]. 4th ed. New York:John Wiley & Sons Inc., 2000.
[12]SARANGI M, MAJUMDAR B C, SEKHAR A S. Stiffness and damping characteristics of lubricated ball bearings considering the surface roughness effect. Part 1:Theoretical formulation [J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2004, 218(6):529-538.
[13]陈於学. 基于接触力学的圆柱滚子轴承振动研究[D]. 武汉:华中科技大学, 2005.
CHEN Yuxue. Research on vibrations of cylindrical roller bearings based on contact mechanics [D]. Wuhan:Huazhong University of Science & Technology, 2005. (in Chinese)
[14]HAMROCK B J, DOWSON D. Ball Bearing Lubrication:The Elastohydrodynamics of Elliptical Contacts [M]. New York:John Wiley & Sons Inc., 1981.
[15]林腾蛟,荣 崎,李润方,等. 深沟球轴承运转过程动态特性有限元分析[J]. 振动与冲击, 2009, 28(1):118-122.
LIN Tengjiao, RONG Qi, LI Runfang,etal. Finite element analysis for dynamic characteristic of a deep-groove ball bearing in motion process [J]. Journal of Vibration and Shock, 2009, 28(1):118-122. (in Chinese)
[16]熊 涛,姚廷强,黄亚宇. 变速工况下球轴承-螺旋锥齿轮多体动力学分析[J]. 昆明理工大学学报(自然科学版), 2016, 41(1):57-63.
XIONG Tao, YAO Tingqiang, HUANG Yayu,etal. Multibody dynamic analysis of ball bearings-spiral bevel gear under variable speed condition [J]. Journal of Kunming University of Science and Technology (Natural Science Edition), 2016, 41(1):57-63. (in Chinese)
[17]邵毅敏,涂文兵. 深沟球轴承三维非线性时变振动特性研究[J]. 振动工程学报, 2013, 26(6):831-838.SHAO Yimin, TU Wenbing. 3D nonlinear time-varying vibration characteristics of deep-groove ball bearing [J]. Journal of Vibration Engineering, 2013, 26(6):831-838. (in Chinese)
Research on rigid-flexible coupling multi-body contact modeling and vibration characteristics of double-row deep-groove ball bearing
JIANG Lingli*1,2,BU Zhongjie1,HAN Qingkai1,2,LI Xuejun1
(1.Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment, Hunan University of Science and Technology, Xiangtan 411201, China;2.School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China )
A rigid-flexible coupling multi-body contact dynamics simulation model of double-row deep-groove ball bearing is proposed, which is based on analysis of the dynamic relationship among components of studied bearing through considering both the elastohydrodynamic lubrication theory and the Hertz contact theory, using the multi-body dynamics analysis software ADAMS combining flexible treatment by the finite element analysis software ANSYS. The equivalent stiffness is developed synthesizing the effect of Hertz contact stiffness and lubrication contact stiffness. The effects of different load, rotational speed and oil film thickness on the vibration characteristics of double-row deep-groove ball bearing are analyzed. The experimental results show that the adequate load can restrain the vibration of double-row deep-groove ball bearings, the increase of rotational speed can intensify the vibration, and the vibration decreases first, then increases with the increase of oil film thickness. The studied work can provide reference for structure optimization design, vibration and noise reduction and running state monitoring of double-row deep-groove ball bearing.
double-row deep-groove ball bearing; rigid-flexible coupling; elastohydrodynamic lubrication; contact stiffness; vibration characteristics
1000-8608(2017)04-0360-07
2016-08-08;
2017-04-14.
国家自然科学基金资助项目(51575177);中国博士后科学基金资助项目(165246);湖南省科技厅重点研发计划资助项目(2015JC3108).
蒋玲莉*(1981-),女,博士,副教授,E-mail:linlyjiang@163.com.
TH133.33
A
10.7511/dllgxb201704005

