基于最优算法的网络控制系统性能研究
李 志 慧,郭 戈,王 兵
(1.大连理工大学 控制科学与工程学院, 辽宁 大连 116024;2.大连海事大学 信息科学技术学院, 辽宁 大连 116026;3.国网吉林省电力有限公司检修公司, 吉林 长春 130021 )
基于最优算法的网络控制系统性能研究
李 志 慧1,郭 戈*2,王 兵3
(1.大连理工大学 控制科学与工程学院, 辽宁 大连 116024;2.大连海事大学 信息科学技术学院, 辽宁 大连 116026;3.国网吉林省电力有限公司检修公司, 吉林 长春 130021 )
针对时隙ALOHA随机调度下的离散网络控制系统,提出一种闭环系统特征矩阵谱条件数与极点配置相结合的控制器设计方法.为了同时考虑控制系统与通信系统性能,将闭环系统特征矩阵谱条件数的最小值问题转化为无约束最优化问题,进而实现控制器设计的优化,降低控制系统对信道吞吐率的要求,使得控制系统与较低吞吐率的通信系统同时稳定,从而实现网络控制系统的稳定.仿真结果表明,该方法设计的控制器具有良好的控制性能,能够在较低吞吐率的信道中稳定运行.
网络控制系统;吞吐率;时隙ALOHA;极点配置;最优化
0 引 言
在制造业、车辆、航空器、航天器、船舶等领域,系统信息与控制信号之间经常需要通过网络传输,每个经过网络连接的系统组成部分都称为节点.当一个系统的闭环回路需要通信信道连接时,被称为网络控制系统,通信信道连接传感器与控制器或控制器与执行器.由于网络资源有限,多个传感器共同分享一个信道时,如果没有协作,信息将会频繁地发生碰撞,子系统不能及时获取信息,最终导致通信系统和控制系统不稳定.因此,多个节点接入网络时,接入信道的方式成为了关注的热点问题.MAC层决定信息接入信道的方式,将通信系统中的MAC层协议与控制系统性能相结合,对于保证通信系统与控制系统的稳定性具有重要意义.
通信系统中MAC层调度协议负责分配多用户共享的信道资源,TDMA是多址协议中的一种信道划分方式,其在时域上实现用户信号正交化.在文献[1-2]中,采用固定分配方式将用户接入网络.在文献[1]中,根据MRBS序列产生的接入序列,子系统周期性地接入网络中,但没有考虑未接入信息因素的影响.文献[2]中,结合最优控制,得出周期性调度序列.然而,固定分配方式很难处理突发和分布式网络控制系统问题.随机分配方式[3]不同于固定分配方式,适合处理分布式网络控制系统的问题,通过退避算法[4]来减少碰撞次数,如纯ALOHA调度协议[5]、时隙ALOHA调度协议[6-7]、载波侦听多路访问/碰撞避免调度协议(CSMA/CA)[8].在随机接入的通信系统中,吞吐率是重要的性能指标,可以利用单位时间内通信系统成功传输信息的概率表示.纯ALOHA调度协议的吞吐率很低;时隙ALOHA调度协议在纯ALOHA调度协议的基础上改进,其吞吐率提高了一倍;CSMA/CA调度协议通过侦听信道提高吞吐率,但增加了成本.本文的通信系统采用时隙ALOHA调度协议,规定各个传感器只能在时隙开始时刻传输数据.在时隙ALOHA调度协议下,网络控制系统转化为一个随机系统.
很多学者对随机系统进行了研究,文献[9]将多个传感器接入网络的方式表述为随机伯努利过程,但并未考虑碰撞问题.文献[10]设计在一个周期内总能保证信息接入的通信协议,但是并没有考虑控制器的设计问题.文献[11]针对具有不同传输速率的子系统设计了随机接入序列.文献[12]将执行器接入网络的过程描述为Markov过程,利用LMI进行控制器设计和稳定性分析.文献[13]将传感器和执行器的接入过程均描述为Markov过程,利用LMI进行控制器设计和稳定性分析.然而它们在通信协议的实现中,仍然需要进一步完善.本文不同于文献[12]和[13]之处是,基于随机调度协议的网络控制系统,采用极点配置的方法分析稳定性性能和设计控制器.
本文采用时隙ALOHA调度协议,将通信系统的吞吐率与控制系统稳定性及控制器设计相结合,实现通信系统与控制系统稳定性的协同设计.
1 问题描述
1.1 系统构成
考虑时隙ALOHA调度协议下单信道离散网络控制系统如图1所示,传感器是时间驱动的,控制器和执行器是事件驱动的,n个传感器共同分享一个信道,通过时隙ALOHA调度协议竞争网络资源.
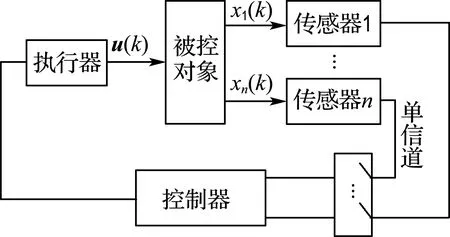
图1 网络控制系统Fig.1 Networked control systems
被控对象描述为离散时不变系统:
x(k+1)=Ax(k)+Bu(k)
(1)
式中:x∈Rn是系统状态;u∈Rm是控制输入;A∈Rn×n和B∈Rn×m分别为适当维数的系统矩阵和控制矩阵.矩阵对(A,B)可控,矩阵B是列满秩的.
1.2 信息接入机制
时隙ALOHA调度协议将时间分成相同长度的时隙T,每个时隙可以发送一个数据包,各个传感器独立地传输数据,传感器i只能在某时隙的开始时刻传输控制信息,如果只有一个传感器i在某时隙传输信息,则传感器i能够成功传输控制信息;如果两个或更多传感器在同一时隙传输信息,则会发生碰撞,任一传感器都不能成功传输信息,未成功发送的控制信息需要等待重传;如果在某时隙传感器都没有传输信息,则信道空闲.

吞吐率S定义为某时隙成功发送数据包的平均个数,网络负载G定义为某时隙发送数据包(成功发送的数据包和未成功发送需要重传的数据包)的平均个数[14].由于各个传感器的统计特性相同,pi=S/n,Gi=G/n.吞吐率S=G(1-G/n)n-1.当网络负载为1时,系统的吞吐率取得最大值,Smax=(1-1/n)n-1.
1.3 时隙ALOHA调度协议下系统模型
由信息接入机制得知,传感器i(i=1,2,…,n)接入网络的过程是一个随机过程.用二值函数δi(k):R→{0,1}表示传感器i在时刻k接入网络的状态.δi(k)=1代表传感器i在时刻k接入网络,其发生的概率为pi;δi(k)=0代表传感器i在时刻k未接入网络,即未接入网络的概率为1-pi.每个传感器接入网络的概率是相同的,为了表达方便,将传感器接入网络的概率表示为p=pi,每个传感器未接入网络的概率表示为1-p=1-pi.矩阵σ(k)=diag{δ1(k),…,δn(k)}表示所有传感器在时刻k接入网络的状态,其由时隙ALOHA调度协议的方式决定信息接入序列,σ(k)∈{η0,η1,…,ηi,…,ηn},ηi(i=1,2,…,n)表示只有传感器i接入网络,仅第i个对角元素为1,其余元素为0的矩阵.η0是零矩阵,表示没有传感器接入网络.
(2)

(3)
结合式(3),系统(1)表示为
x(k+1)=[A+BKσ(k)]x(k)
(4)
本文的目的是设计使得时隙ALOHA调度协议下单信道离散网络控制系统稳定的控制器,分析时隙ALOHA调度协议下,通信系统吞吐率与控制系统稳定性和系统动态特性的关系.
2 稳定性分析
对于给定传感器个数的系统,其吞吐率S=pn,为了保证网络控制系统的稳定,一方面需要保证控制系统的稳定性,一方面需要保证通信系统的稳定性.通信系统稳定性[15]的一种解释为系统的输出量不小于系统的输入量,即系统实际吞吐率小于系统所能容纳的最大吞吐率.本文结合两方面的稳定性展开讨论.接下来介绍控制系统的稳定性.
引理1 控制器(3)可以使系统(4)均方稳定[16],如果存在矩阵
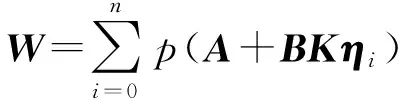
(5)
是Schur稳定的,⊗代表克罗内克积.
定理1 系统(4)是均方稳定的,如果存在控制器(3),满足
ρ(A⊗A+(S/n)(A⊗BK+BK⊗A+ (BK⊗BK)Φ))<1
(6)

证明 根据式(5)得

(7)
时隙ALOHA调度协议下的单信道网络每次只能传输一个传感器信息,因此有
(8)
其中I∈Rn×n.进一步有
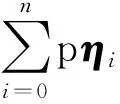
(9)
因此得出:
W=A⊗A+(S/n)(A⊗BK+BK⊗A+ (BK⊗BK)Φ)=p(AK⊗AK)+(1-p)(A⊗A)+p(BK⊗BK)(Φ-I)
(10)
其中AK=A+BK.定理1得证.
注:定理1也可以直接利用状态误差矩阵证明.
定义1Pmax是能使系统稳定的信息未接入网络概率的上界,即在信息未接入网络概率小于Pmax的情况下,网络控制系统是稳定的.
注:Pmax反映了具有开环的系统的鲁棒稳定性,当Pmax较大时,系统仍保持稳定,则系统具有较好的性能,事实上,在传输过程中具有信息丢失的系统的动态性能也是由闭环系统的极值点决定的.很明显,如果闭环系统是名义稳定的,则Pmax大于零.直接求信息未接入网络概率是比较困难的,将其转化为求Pmax的下界.

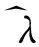
λ^
∈spec(W),存在λ∈spec(AK⊗AK)满足

λ^-pλ≤

(11)

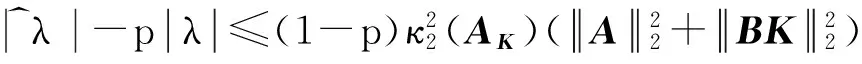
λ^-pλ≤(1-p)κ22(AK)(A22+BK22)
(12)
式(12)可写为
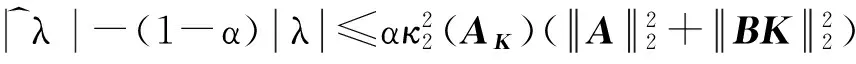
λ^-(1-α)λ≤ακ22(AK)(A22+BK22)
(13)
其中p=1-α.

(14)
由式(14)可得因此系统(4)在控制器(3)下是均方稳定的.
由式(14)得出
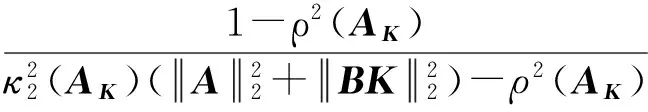
α< (15)
根据式(11)得出由于
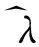
λ^
是任意的,控制器K可以使系统(4)均方稳定.
注:从通信角度,当网络负载G=1时,系统的吞吐率取得最大值,Smax=(1-1/n)n-1,由于系统的吞吐率与未接入概率之间存在关系S=pn=(1-α)n,如果通信系统是稳定的,则一定存在Smax≥S,(1-1/n)n-1≥(1-α)n.
3 控制器设计
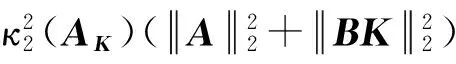
选择控制器矩阵K∈Rm×n使得闭环系统矩阵A+BK的谱表示为任意基数为n的自共轭复数,换言之,存在一个可逆的矩阵T∈Rn×n,满足
(A+BK)T=TΛ
(16)
式中:Λ为实伪对角阵,满足

其中αl±βli(l=1,2,…,n1)、γv(v=1,2,…,n-2n1)为闭环系统的特征值.
式(16)可以被表示为
AT-TΛ+BG=0
(17)
G=KT
(18)
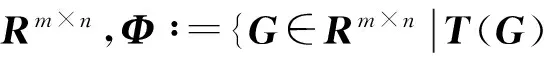
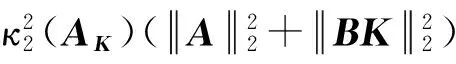

(19)
对于非零数ω,Ji(Gi)=Ji(ωGi),使得海森矩阵在最小点奇异,为克服此困难,选择一个辅助目标函数[17]

(20)
给定G的初始值,利用梯度解下降法求能使辅助目标函数ψq(G)最小的T(G),进而求出具有鲁棒性能的控制器K=GT-1.





4 数值仿真
图2表示系统的状态误差,验证本文设计控制器的有效性.图3中(a)和(b)分别代表传感器1和传感器2接入网络的序列,“1”代表传感器正在传输信息,“0”代表传感器没有传输信息.图3(c) 中的“1”代表信道正在传输信息,“0”代表信道处于空闲状态.
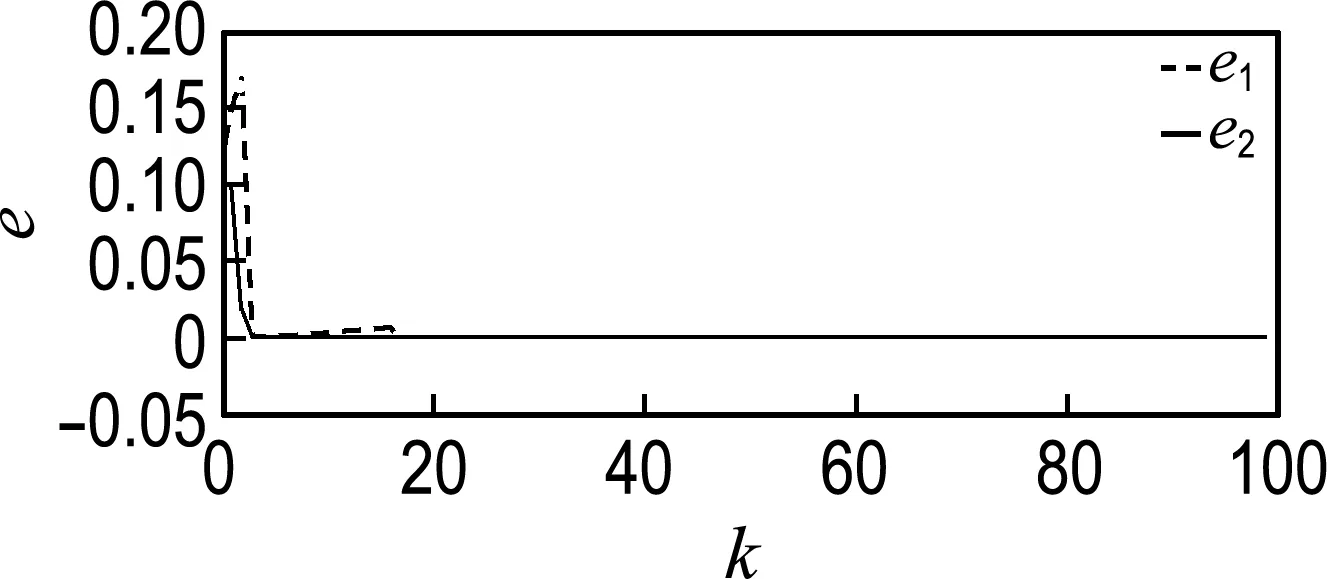
图2 优化极点配置控制器下系统状态误差Fig.2 The system state error under the optimal polenassignment controller

(a) 传感器1

(b) 传感器

(c) 信道状态
图3 接入序列
Fig.3 The access sequence

图4 次优化极点配置控制器下系统状态误差Fig.4 The system state error under suboptimal polenassignment controller
5 结 语
本文针对时隙ALOHA调度协议下单信道离散网络控制系统,基于闭环系统特征矩阵谱条件数与极点配置设计控制器.首先将时隙ALOHA 调度协议下网络控制系统建模成离散的随机网络控制系统,然后推出通信系统吞吐率与控制系统动态特性的关系,最后利用MATLAB仿真工具,验证了本文设计方法的有效性.本文未考虑退避过程产生延时的影响,今后将对其进一步研究.
[1]GUO Ge, WEN Shixi. Protocol sequence and control co-design for a collection of networked control systems [J]. International Journal of Robust and Nonlinear Control, 2016, 26(3):489-508.
[2]REHBINDER H, SANFRIDSON M. Scheduling of a limited communication channel for optimal control [J]. Automatica, 2004, 40(3):491-500.
[3]TOBAGI F A. Multiaccess protocols in packet communication systems [J]. IEEE Transactions on Communications, 1980, COM-28(4):468-488.
[4]KWAK B-J, SONG N-O, MILLER L E. Performance analysis of exponential backoff [J]. IEEE Transactions on Networking, 2005, 13(2):343-355.
[5]CARLEIAL A R, HELLMAN M E. Bistable behavior of ALOHA-type systems [J]. IEEE Transactions on Communications, 1975, COM-23(4):401-410.
[6]ZAALOUL A, EL AATTAR M B, HANINI M. Sharing channel in IEEE 802. 16 using the cooperative model of slotted ALOHA [J]. International Journal of Computer & Organization Trends, 2013, 3(9):439-443.
[7]GHEZ S, VERDU S, SCHWARTZ S C. Stability properties of slotted ALOHA with multipacket reception capability [J]. IEEE Transactions on Automatic Control, 1988, 33(7):640-649.
[8]YENER A, ROSE C, YATES R D. Optimum power scheduling for CDMA access channels [C] // Conference Record / IEEE Global Telecommunications Conference. Piscataway:IEEE, 1997:1499-1503.
[9]LIU Kun, FRIDMAN E, JOHANSSON K H. Networked control with stochastic scheduling [J]. IEEE Transactions on Automatic Control, 2015, 60(11):3071-3076.
[10]SHUM K W, CHEN C S, SUNG C W,etal. Shift-invariant protocol sequences for the collision channel without feedback [J]. IEEE Transactions on Information Theory, 2009, 55(7):3312-3322.
[11]WONG W S. New protocol sequences for random-access channels without feedback [J]. IEEE Transactions on Information Theory, 2007, 53(6):2060-2071.
[12]GUO Ge. Linear systems with medium-access constraint and Markov actuator assignment [J]. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2010, 57(11):2999-3010.
[13]GUO Ge. Feedback control with scheduled communication sequences and random delays [J]. International Journal of Control, Automation and Systems, 2010, 8(6):1342-1348.
[14]ABRAMSON N. Packet switching with satellites [C] // AFIPS ′73 Proceedings of the June 4-8, 1973, National Computer Conference and Exposition. New York:ACM, 1973:695-702.
[15]BIANCHI G. Performance analysis of the IEEE 802.11 distributed coordination function [J]. IEEE Journal on Selected Areas in Communications, 2000, 18(3):535-547.
[16]HU S, YAN Weiyong. Stability robustness of networked control systems with respect to packet loss [J]. Automatica, 2007, 43(7):1243-1248.
[17]LAM J, YAN Weiyong. Pole assignment with optimal spectral conditioning [J]. Systems and Control Letters, 1997, 29(5):241-253.
Performance study of networked control system based on optimal algorithm
LI Zhihui1,GUO Ge*2,WANG Bing3
(1.School of Control Science and Engineering, Dalian University of Technology, Dalian 116024, China;2.School of Information Science and Technology, Dalian Maritime University, Dalian 116026, China;3.State Grid Jilin Maintenance Company, Changchun 130021, China )
For the discrete networked control system under slotted-ALOHA scheduling protocol, a controller design method is proposed based on the spectrum condition number of eigenmatrix and pole assignment of the closed system. Considering both of the performances of control system and communication system, the minimization problem of the spectrum condition number of eigenmatrix for the closed system is looked as unconstrained optimization problem to realize the optimization of the controller and reduce the need of channel throughput by control system, which can simultaneously stabilize the control system and the low-throughput communication system, and finally realize the stabilization of the networked control system. The simulation results prove that the controller designed by the method is of good control performance and can guarantee the stability in the channel with low throughput.
networked control system; throughput; slotted-ALOHA; pole assignment; optimization
1000-8608(2017)04-0418-06
2016-09-24;
2017-05-23.
国家自然科学基金资助项目(61273107,61573077).
李志慧(1990-),女,博士生,E-mail:lizhihui1650@163.com;郭 戈*(1972-),男,教授,E-mail:geguo@yeah.net.
TP18
A
10.7511/dllgxb201704013

