剧烈变温环境下保温材料除湿过程数值模拟
陈 磊,王 树 刚*,张 腾 飞,房 天 宇
(1.大连理工大学 建设工程学部, 辽宁 大连 116024; 2.中国建筑东北设计研究院有限公司, 辽宁 沈阳 110016 )
剧烈变温环境下保温材料除湿过程数值模拟
陈 磊1,王 树 刚*1,张 腾 飞1,房 天 宇2
(1.大连理工大学 建设工程学部, 辽宁 大连 116024; 2.中国建筑东北设计研究院有限公司, 辽宁 沈阳 110016 )
基于Darcy渗流扩展模型,并结合体积平均假设构建能量及质量守恒方程,模拟剧烈变温环境下保温材料的除湿过程.分别采用相对湿度20%(24 ℃)及干空气两种送风方式对该种保温材料的对流除湿过程进行数值模拟,进而讨论不同时刻温度、水蒸气浓度、液态水及冰的变化规律.研究表明,Darcy渗流扩展模型可以较好地反映出多孔保温材料在表面气流冲刷条件下其内部水蒸气的非线性流动特性,同时两种送风方式均可有效降低多孔保温材料因剧烈温变而引起的水分积聚,其相应的除湿率可分别达到70%和90%.
保温材料;Darcy渗流;水分积聚;除湿率
0 引 言
应用于交通工具、冷库和加热炉高温区的多孔保温材料常处于剧烈变温环境中,如飞机在运行过程中,通常伴随着环境温湿度间歇性的变化,其覆盖的多孔保温材料易出现水分累积;在冷库制冷过程中,急剧降温将导致水蒸气直接凝华于保温材料孔隙.累积的水分若不能被及时去除必将引发结构腐蚀、保温隔热性能减弱及因增重而提升运营成本等诸多负面效应[1-2].因此,在剧烈变温环境下,对保温材料内水分迁移和相变的研究,寻求有效的除湿方案以提升除湿效果便显得尤为重要.
保温材料中的水分累积是个长期而缓慢的过程.水分通常以水蒸气、液态水和冰三种相态存于保温材料孔隙,若水分以两种或三种相态共存,相变的发生便无法避免.水的相变过程又伴随着能量的得失,从而使得水分在保温层中形成热湿耦合的复杂传递过程.正如飞机在运行过程中,水蒸气透过维护结构渗入保温层,受环境温湿度变化的影响,水蒸气极易发生相变并以液态水或冰的形式存于孔隙.通常情况下,保温层中的液态水累积量比较少,其自身重力无法克服毛细作用而静止于孔隙.因此,保温层中水分的迁移只是通过水蒸气在孔隙间自由扩散或低速流动得以实现[3-4],其中,保温层内由浓度差引起水蒸气的自由扩散及孔隙间水蒸气的Darcy渗流主要为水分迁移过程的线性传递形式[5-6],当多孔材料表面受空气高速冲刷或与环境间存有较大温差时,其内部水蒸气的流动将会呈现出明显的非线性[7],为对此种非线性流动特性进行准确描述,以Navier-Stokes方程为基础的Darcy扩展模型近些年来被广泛关注,且进行了大量的理论及实验研究[8].
本文以飞机运行环境为背景,提出在飞机保温层舱内一侧增设风道及改变现有空调系统中加湿设备位置的设计构想,运用数值模拟的方法对保温层除湿过程中的温度、水蒸气浓度、液态水和冰的变化规律进行预测.
1 物理模型
飞机保温层的多孔材料的物性参数详见表1.在飞机的单个运行周期内,机体外壁面温度可从-35 ℃变化到35 ℃,温差在70 ℃以上(飞机高速运行时,金属壳体与大气环境会摩擦生热,因此,壁面温度高于实际大气静态温度).为满足舱内人员对环境温湿度要求,在空调系统的调控下,舱内环境维持舒适性温度24 ℃,而考虑到飞机的安全运行、成本的节约,舱内相对湿度仅维持在10%~30%,以满足人体的基本要求.由于飞机所处的大气环境及舱内的温湿度环境较为均匀,且飞机保温层是由布置于不同隔断框架内若干块保温材料堆砌而成,因此为提高计算效率,选取飞机单块保温材料建立二维物理模型.模型及尺寸详见图1.在现有飞机保温层的构造设计基础上,本文在保温层舱内一侧增设了风道,风道气流与保温层直接接触,通过含湿量较低的空气(或干空气)对保温层的高速冲刷实现除湿目的.
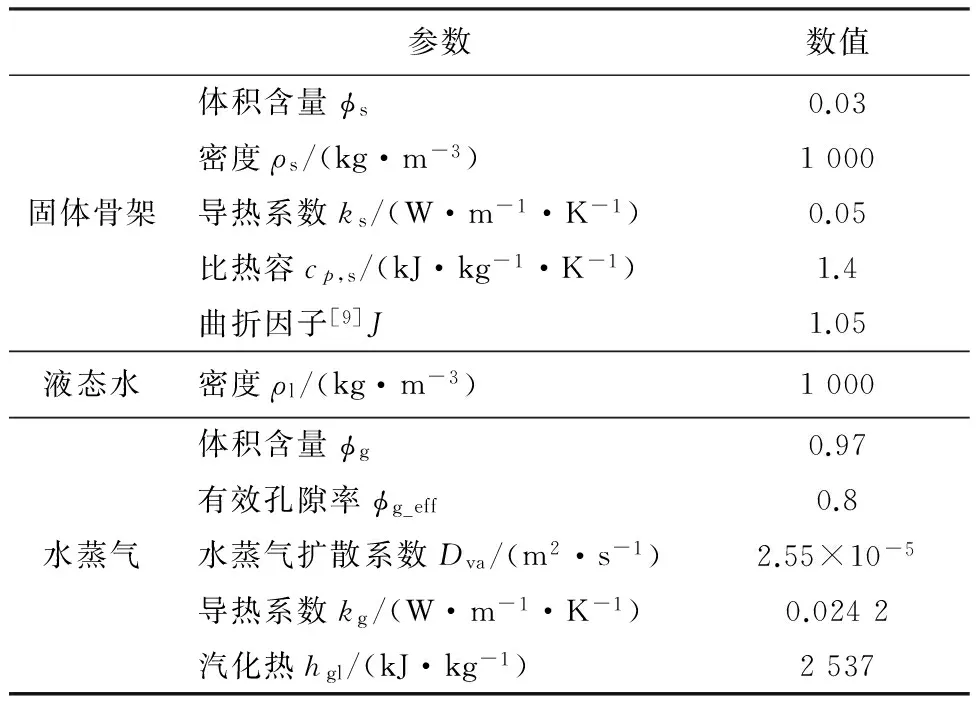
表1 CFD模型中物性参数Tab.1 Adopted property parameters in the CFD modeling
风道送风口气流直接来自于空调机组,飞机空调系统的送风流程如下:飞机发动机从大气环境中吸入空气(高空空气中水分含量极低,可近似认为干空气),发动机的高速运转,大幅提升了所吸入空气的温度和压力,高温高压的空气(相对高空环境中的空气)经空调包与回风混合、调节送风温度和压力(高空中舱内压力一般在80 kPa)以及加湿处理,最终送入舱内.根据飞机空调系统的送风流程和文献[10]的双风道设计设想,本研究提出了两种不同的风道送风流程:方案1,将从发动机吸入的干空气降温至35 ℃,并按照现有的空调系统运作流程,将相对湿度提升至11%(含湿量与客舱内24 ℃、相对湿度20%的空气相同),送入风道,通过高温空气高速冲刷(风速1.5 m/s)实现除湿的目的,并在末端装置处设置空气过滤器和二次温度调控系统,最终将24 ℃、大于20%相对湿度的空气送入舱内(因除湿过程中,保温层中渗出的水蒸气融入风道中的空气,提升了风道空气的含湿量).方案2,发动机吸入干空气后,经温度和压力调节(如上35 ℃)直接引入风道,以干空气完成对保温层的冲刷,并在末端装置处进行温度调控和加湿处理,最终将24 ℃、20%相对湿度空气送入客舱.

(a) 物理模型

(b) 边界条件
图1 物理模型及边界条件
Fig.1 Physical model and boundary condition
2 数学模型
本研究基于以下基本假设使得数学模型封闭,并耦合求解能量和质量传递方程:
(1)水蒸气在干空气携带下进行流动(即共享速度);
(2)多孔材料为非吸湿性材料[11](不考虑短时间内多孔材料的吸附作用);
(3)液态水无法克服毛细阻力发生迁移;
(4)时刻满足热力学平衡,仅在水蒸气达到饱和时发生相变.
当空气快速冲刷多孔材料表面时,其在多孔材料内部的流动会呈现出很强的非线性,自由扩散与Darcy渗流模型无法满足求解要求,因此,选取Brinkman-Forchheimer extended Darcy模型(即Darcy扩展模型)对动量方程和连续性方程进行数学描述[12]:
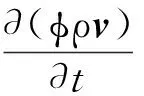
(1)

(2)
式中:φ为孔隙率;ρ为密度,kg/m3;v为气相速度,m/s;t为时间,s;p为气相压力,Pa;τ为剪切应力,Pa;g为重力加速度,m/s2;β为热扩散系数,K-1;ΔT为特定参考温度下的温差,K;μ为动力黏度,Pa·s;1/α为黏性阻力系数,1/m2;C2为惯性阻力系数,1/m.由Darcy扩展模型可知,其实质就是在标准的Navier-Stokes方程中,通过源项引入黏性及惯性阻力,从而利用动量平衡原理描述出多孔介质内流体的流动特性.
基于假设条件(4),水蒸气在多孔材料的相变条件是以其是否达到饱和为判断依据.水蒸气的质量平衡方程可表达为[12]
(3)
式中:ρv为水蒸气密度,kg/m3;Deff为有效扩散系数,m2/s;Sv为相变量,kg/(m3·s).
基于体积平均假设建立能量守恒方程,表达形式如下[13]:

(4)
式中:ρ为各水分相态的密度,kg/m3;cp为比热容,kJ/(kg·K);T为温度,K;keff为有效导热系数,W/(m·K);ST为相变热,kJ/(m3·s).下标中“g”“l”“s”分别代表湿空气、液态水及固体骨架.
本文的数学模型同时涉及纯流体计算域和多孔介质计算域,因此,在数值模拟过程中计算域的边界耦合问题尤为关键:纯流体流动主要遵循Navier-Stokes方程组实现对空气流动的数学描述;而多孔材料区域则依据Darcy扩展模型描述空气流动.两计算域采用Masmoudi等[14]提出的方法进行交界面的耦合,即在交界面处严格遵循质量流量与热流量的守恒,表达式如下(式(5)和(6)分别为干空气及水分的质量平衡方程):

(5)

(6)
式中:n为单位向量;Fm为质量流量,kg/s.交界面处,热流量

(7)
式中:h为焓,J;Fh为热流量,W.
针对本文所求解的实际问题:通过在飞机保温层舱内一侧增设风道,对单个飞机运行周期的除湿效果进行预测.结合建模的基本假设可知,在交界面处理时,式(5)中不考虑液态水和结合水的迁移.
3 物理模型求解
简化后的物理模型如图2(a)所示.根据飞机的运行环境对保温层的边界条件定义如下:底部为与飞机壳体接触的密封侧,其与环境之间并无质量交换,温度是飞行高度的函数(变化规律详见图1(b));保温层左右两侧与隔断框架接触处即绝缘绝热边界;保温层顶部受高温的高速空气冲刷,与风道空气进行热湿交换.模型的网格划分如图2(b)所示,在风道和保温层的计算域内分别生成单位尺寸为1 mm的结构化网格,并在边界线处进行耦合,网格生成数量分别为10 000和15 000.待网格划分后,运用Fluent软件对动量方程、能量及质量守恒方程(编程实现)进行求解.计算过程中通过试算确定风道及多孔区域雷诺数,其大小分别为5.23×104和3.33,根据雷诺数的大小动量方程分别选择湍流及层流模型.在计算精度上采用二阶迎风格式,压力差分为PRESTO格式,并结合SIMPLE算法完成速度和压力的耦合求解.因风道持续通入高速流体冲刷客机保温层,风道中的强制对流以及保温层中渗流速度几乎不受环境温度的影响,可认为模型求解过程中速度场恒定且残差在10-3以下作为收敛的判定依据.物理过程为非稳态,经时间独立性验证以3 s为一个时间步长,空间迭代3 000次,各标量方程计算残差均控制在10-6以下.

(a) 简化物理模型

(b) 网格划分
图2 简化物理模型及网格划分
Fig.2 Simplified physical model and grid division
4 分析与讨论
为凸显除湿效果,初始时刻假定飞机保温层中液态水体积分数为0.001.在方案1的送风流程中,保温层内水分各相态随时间的变化规律如图3(a)所示.由图可知,该方案具有较好的除湿效果,除湿率可达70%以上:飞机运行前20 min,保温层的水分含量迅速下降.这是由于在初始时刻保温层中的水蒸气为饱和状态(假设(4)),孔隙内的水蒸气分压力远高于风道,在对流和扩散双重作用下液态水以蒸发的形式从保温层渗出,融入风道中的空气.在飞机运行至25 min时,风道中的水蒸气浓度已高于保温层的部分区域,在水蒸气分压力及对流的作用下,风道中的高浓度水蒸气(相对多孔材料)开始向保温层渗入,此时,飞机已逐渐进入巡航阶段,客舱内外环境的温湿度相对恒定,且壳体内壁面附近的保温层孔隙的温度已降至冰点以下,液态水逐渐凝结成冰,并随时间的增加水分累积量(水蒸气凝华)缓慢上升.当飞机进入着陆阶段(150 min)时,环境温度逐渐回升,直至160 min时,保温层中部分含冰孔隙的温度回升至冰点以上,冰逐渐融化成水.随着温度的持续升高,保温层中的水蒸气浓度高于风道,风道除湿效果再次发挥作用,在水蒸气分压力的驱动下,水分从多孔保温层迅速渗出.
图3(b)展现了风道通入干空气所呈现的水分各相态的变化规律(方案2).由图可见,该方案的除湿效果明显强于方案1,除湿率可达90%以上.与方案1类似,飞机运行前20 min,保温层中的水分含量迅速下降.而与方案1的区别在于,飞机进入巡航阶段后,保温层中的水分含量持续下降.虽然随着保温层近壳体侧温度的降低,孔隙中水蒸气饱和分压力骤减,但水蒸气浓度仍高于风道的(干空气),水分将以升华的方式继续向风道渗入,但因保温层两侧(飞机壳体侧与风道侧)水蒸气分压力差的缩小,脱水速率会有所减缓.而飞机进入着陆阶段后,环境温度开始回升,水蒸气饱和分压力逐渐升高,保温层两侧水蒸气分压差加大,脱水速率再次加快,待飞机飞行结束时,保温层孔隙中水分基本蒸干.图4为速度场分布.
因各时刻两种送风方案的温度、水蒸气浓度、液态水和冰的分布规律类似,仅以方案1的参数分析为例.图5展示了飞机起飞10 min时,风道及保温层的温度、水蒸气浓度和液态水分布.风道中由于高温空气的冲刷,温度恒定在35 ℃,仅在风道出口的下方略有温降,原因在于保温层内低温(相对风道)空气的渗出.相比于风道,保温层的边界条件比较复杂,一侧受高速流动的高温空气冲刷,而另一侧与飞机壳体的内壁面接触并随飞行高度发生温变(详见图1(b)).结合速度与温度的分布,高温流体沿着流线从保温层的左侧渗入,使风道侧保温层部分区域的温度迅速升至35 ℃(风道温度),根据动量守恒原理,保温层中的低温空气将从其右侧渗出,且在垂直方向上流速逐渐衰减(向着壳体方向),致使近壳体侧能量传递过程近似为导热,在对流及导热的共同作用下形成如图5(a)所示的温度场.高温区域孔隙中水分在水蒸气的分压力差及对流作用下以蒸发的方式逐渐渗入风道,此时,贴近风道侧的保温层中的液态水已全部蒸干,水蒸气浓度与风道完全一致(35 ℃相对湿度11%).根据含水孔隙水蒸气饱和的假设,含水孔隙附近的水蒸气浓度始终介于风道与该温度下饱和浓度间并形成浓度梯度,见图5(b).

(a) 送风相对湿度20%

(b) 送入干空气
图3 保温层水分随时间的变化
Fig.3 The moisture changes with time

(a) 风道速度场分布

(b) 保温层速度场分布
图4 速度场分布
Fig.4 The velocity field distribution

(a) 温度场

(b) 水蒸气浓度
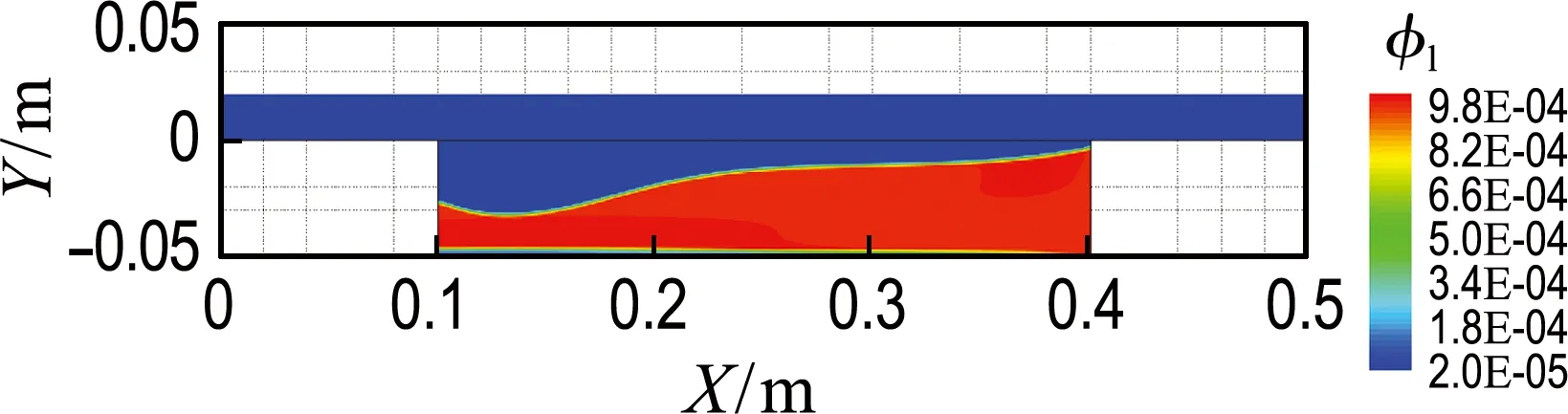
(c) 水体积分数
图5 10 min时,保温层内主要参数分布
Fig.5 At 10 min, the major parameters distribution in thermal insulation layer
图6为飞机运行1 h时,风道和保温层中温度、水蒸气浓度、液态水和冰体积分数的分布.因风道入口持续通入温湿度恒定的空气,风道内气流温度和水蒸气浓度随时间变化微弱.此时,飞机已进入巡航阶段,保温层两侧温湿度条件相对恒定(壳体内壁面温度降至-21 ℃).如图6(a)所示,保温层上下两侧形成较大温度梯度.原因在于,随着时间的推移,保温层风道一侧,因高温空气(风道中相对高温)不断渗入(流线见图4),其内部的温升区域逐渐扩大;而在近壳体侧,由于外界环境的低温导入,低温区域(低于保温材料初始温度)亦有明显蔓延.如图6(b)所示,水蒸气浓度除在近内壁面及右侧出现高值点外均与风道相近,原因在于,壳体侧水蒸气浓度已达饱和且低于其在风道内的浓度,凝结的冰不会相变升华.相反,因保温材料上下两侧稳定的边界条件,水蒸气会以相对恒定速度凝华(详见图6(d)).
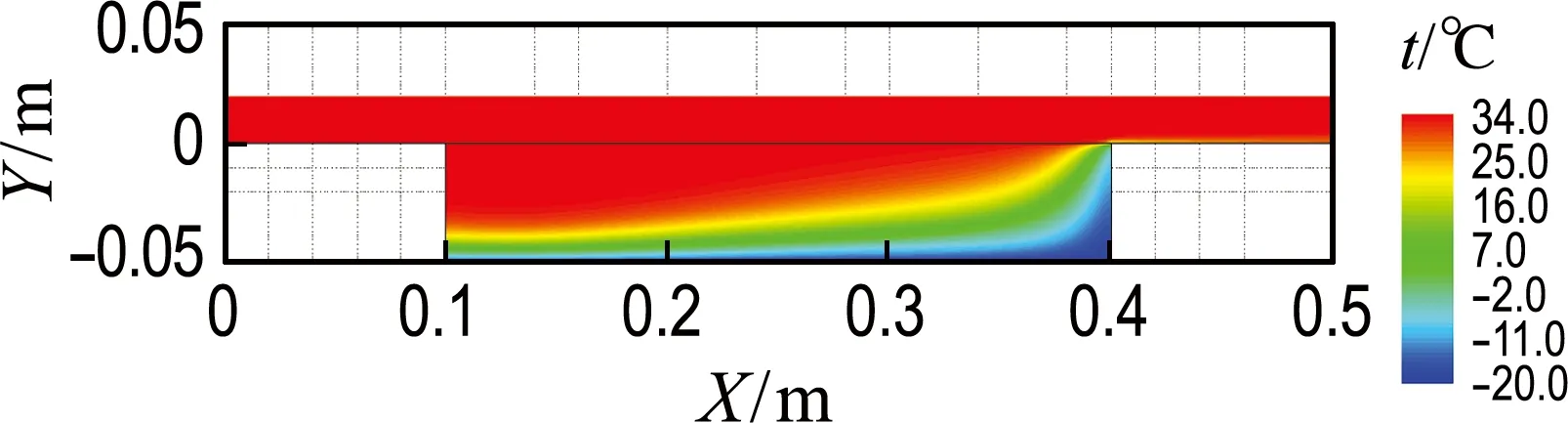
(a) 温度场
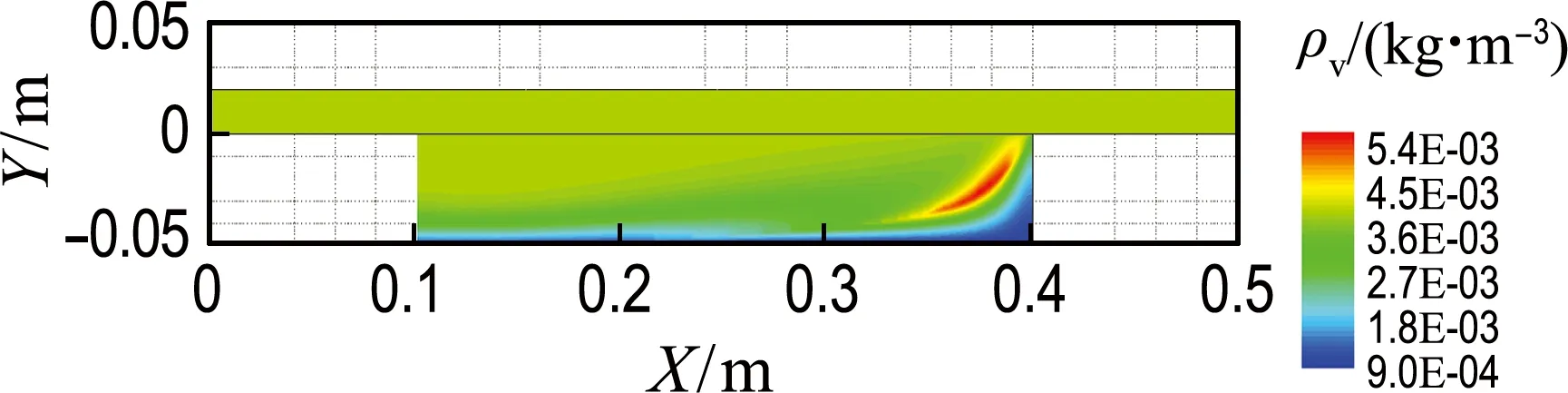
(b) 水蒸气浓度

(c) 水体积分

(d) 冰体积分数
图6 1 h时,保温层内主要参数分布
Fig.6 At 1 h, the major parameters distribution in thermal insulation layer
图7为最终时刻,保温层中各主要参数的分布.由温度分布可知,因飞机着陆阶段大气温度的逐渐回升(见图1(b))以及风道的气流对保温层顶端的恒温冲刷,致使保温层两端出现高温(35 ℃) 区域的扩大,在两高温区域间形成了低温区,且在空气渗出处达低温极值(在对流作用下低温气体不断被带出).由水蒸气浓度分布可知,因飞行周期结束时,仍有液态水存于飞机壳体侧保温层孔隙,基于假设(4),此部分孔隙中的水蒸气仍为该温度下的饱和态,水蒸气会在保温层含水孔隙与风道间形成浓度梯度,与空气流场相对应形成如图7(b)的浓度分布规律.

(a) 温度场

(b) 水蒸气浓度

(c) 水体积分数
图7 3 h时,保温层内主要参数分布
Fig.7 At 3 h, the major parameters distribution in thermal insulation layer
5 结 论
(1)在风道通入空气温度为35 ℃、相对湿度为11%的初始条件下,保温层内水分迁移呈现出:在飞机起飞阶段,随着大气温度的下降,保温层温降引起的水蒸气分压力下降,导致风道除湿速率减小;在飞机巡航阶段,因舱内外温湿度环境稳定,水分在保温层中将线性凝结;而在飞机着陆阶段,随着大气温度的回升,保温层温升引起的水蒸气分压力提高,致使其中水分蒸发再次混入风道气流.可见除湿主要集中于飞机起飞与着陆阶段,增设风道使其除湿率达70%以上.
(2)当在增设的风道通入高温干空气的条件下,保温层内水分迁移呈现出:在飞机运行的各阶段,水蒸气从保温层持续渗出;受大气变温的影响,水分迁移速率呈现间歇性变化.相比于风道中通入湿空气的除湿效果,除湿率可达90%以上.
(3)在保温层舱内一侧引入风道的设计方案,能使多孔材料内的水分沿着稳定的路径迁移,可在飞机运行过程中实现除湿,从而降低运营成本、延长现有飞机保温层除湿的时间.此外,此部分水蒸气增加了舱内空气的含湿量,进一步降低了舱内加湿器的湿负荷.
[1]BRETZ E A. Putting humidity in its place [J]. IEEE Spectrum, 2003, 40(3):28-30.
[2]JENAB K, RASHIDI K. Operational reliability assessment of an aircraft environmental control system [J]. Reliability Engineering & System Safety, 2009, 94(2):456-462.
[3]刘 敏,俞炳丰,胡张保. 室温磁制冷最新研究进展[J]. 制冷学报, 2007, 28(4):1-11.
LIU Min, YU Bingfeng, HU Zhangbao. New development of research on room temperature magnetic refrigeration [J]. Journal of Refrigeration, 2007, 28(4):1-11. (in Chinese)
[4]张 珍,谢 晶. 带有上下均风孔板的速冻装置中流场及温度场的数值模拟[J]. 制冷学报, 2009, 30(5):36-40.
ZHANG Zhen, XIE Jing. Numerical simulation on flow and temperature fields in quick freezer with perforated plates [J]. Journal of Refrigeration, 2009, 30(5):36-40. (in Chinese)
[5]OLUTIMAYIN S O, SIMONSON C J. Measuring and modeling vapor boundary layer growth during transient diffusion heat and moisture transfer in cellulose insulation [J]. International Journal of Heat and Mass Transfer, 2005, 48(16):3319-3330.
[6]ERRIGUIBLE A, BERNADA P, COUTURE F,etal. Simulation of convective drying of a porous medium with boundary conditions provided by CFD [J]. Chemical Engineering Research & Design, 2006, 84(A2):113-123.
[7]CHEN G, HADIM H A. Forced convection of a power-law fluid in a porous channel:numerical solutions [J]. Heat and Mass Transfer, 1998, 34(2/3):221-228.
[8]VAFAI K, KIM S J. On the limitations of the Brinkman-Forchheimer-extended Darcy equation [J]. International Journal of Heat & Fluid Flow, 1995, 16(1):11-15.
[9]DOUTRES O, ATALLA N, DONG K. A semi-phenomenological model to predict the acoustic behavior of fully and partially reticulated polyurethane foams [J]. Journal of Applied Physics, 2013, 113(5):054901.
[10]张腾飞,沈润霖,林钊信,等. 一种用于飞机的双风道墙体:2013100981718 [P]. (2013-03-25) [2015-07-22].
ZHANG Tengfei, SHEN Runlin, LIN Zhaoxin,etal. Double air channel wall for airplane:201300981718 [P]. (2013-03-25) [2015-07-22]. (in Chinese)
[11]俞昌铭. 多孔材料传热传质及其数值分析[M]. 北京:清华大学出版社, 2011.
YU Changming. Numerical Analysis of Heat and Mass Transfer for Porous Materials [M]. Beijing:Tsinghua University Press, 2011. (in Chinese)
[12]KAVIANY M. Principles of Heat Transfer in Porous Media [M]. New York:Springer-Verlag, 1995.
[13]CHEN Lei, WANG Shugang, LI Guohui,etal. CFD modeling of moisture accumulation in the insulation layers of an aircraft [J]. Applied Thermal Engineering, 2016, 102:1141-1156.
[14]MASMOUDI W, PRAT M. Heat and mass transfer between a porous medium and a parallel external flow-Application to drying of capillary porous materials [J]. International Journal of Heat and Mass Transfer, 1991, 34(8):1975-1989.
Numerical simulation on dehydration process in thermal insulation material subject to severe temperature change environment
CHEN Lei1,WANG Shugang*1,ZHANG Tengfei1,FANG Tianyu2
(1.Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China;2.China Northeast Architectural Design & Research Institute Co., Ltd, Shenyang 110016, China )
Based on the extended Darcy seepage model, the energy and mass conservation equations are coupled together by volume average hypothesis to simulate the dehydration process in thermal insulation material subject to severe temperature change environment. The mathematical model is developed to simulate the process of convection dehydration by air of 20% relative humidity (at 24 ℃) and dry air respectively. The changing regularities of the temperature, water vapor concentration, liquid water and ice at different time are analyzed. The research results show that the extended Darcy seepage model can reflect the nonlinear flow characteristics of water vapor during air flows over the porous thermal insulation materials. Two kinds of ventilation modes can effectively reduce moisture accumulation in the porous thermal insulation materials subject to severe temperature change environment, and the dehydration rate can reach 70% and 90% respectively.
thermal insulation materials; Darcy seepage; moisture accumulation; dehydration rate
1000-8608(2017)04-0345-07
2016-11-05;
2017-06-01.
“九七三”国家重点基础研究发展计划资助项目(2012CB720105).
陈 磊(1983-),男,博士生,E-mail:L_lei_l@163.com;王树刚*(1963-),男,博士,教授,博士生导师,E-mail:sgwang@dlut.edu.cn.
TK124
A
10.7511/dllgxb201704003

