基于知识推理和二阶振荡粒子群算法的桩基础优化设计

于 亚 洲，王 胤，杨 庆*，陈 龙

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；2.大连理工大学 土木工程学院， 辽宁 大连 116024 )

基于知识推理和二阶振荡粒子群算法的桩基础优化设计

于 亚 洲1，王 胤1，杨 庆*1，陈 龙2

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；2.大连理工大学 土木工程学院， 辽宁 大连 116024 )

为辅助设计者准确高效地完成桩基础设计工作，降低工程造价，基于知识推理和二阶振荡粒子群算法开发出一套桩基础优化设计系统．系统通过结合C#语言和CLIPS推理机实现桩基础埋深推理功能，进而求出当前场地条件下的最优桩长．选择以工程造价为目标函数设计优化数学模型，根据已知的最优桩长简化优化变量．选用二阶振荡粒子群算法作为优化算法，结合桩基础规范设计约束条件，编制出桩基础优化程序．最后以某十层实验教学楼为例进行分析，证明了本优化算法的可行性．

知识推理；二阶振荡粒子群算法；桩基础优化设计；工程造价

0 引 言

桩基础是一种历史悠久、发展迅速、应用广泛的深基础，因其具有承载力高、稳定性好、沉降量小且均匀等优点而广泛应用于高层建筑和对沉降要求较高的建筑．然而桩基础设计和施工是一个复杂的系统工程，如果能在设计上进行系统的优化，将在很大程度上节约工程造价．近年来，随着计算机科学技术的迅速发展，桩基础优化设计理论可以通过高效率的计算机程序实现和应用，这将有助于从设计上解决群桩基础的优化问题，具有较高的实用性．

桩基础优化设计主要包括设计理论、数学模型和优化算法三部分，其中优化算法的优劣会影响到计算结果的精确性和计算效率．目前，有关学者已将数学规划法[1-2]、人工神经网络法[3]、遗传算法[4]和粒子群算法[5-6]引入桩基础优化中，并可以结合工程案例进行优化分析．令人遗憾的是，以上算法对于求解桩基础优化设计问题都存在自身局限．数学规划法要求目标函数显式表示，而且需要满足一定理论条件才能收敛；人工神经网络法难以精确分析优化数学模型中的约束变量，计算结果精度有限；遗传算法难以准确选取参数，程序编写复杂，计算效率不高；粒子群算法在初始粒子不满足约束条件时不易实现自我调节，无法兼顾计算效率与计算精度．

考虑到以上困难，本文提出一种基于知识推理和二阶振荡粒子群算法的桩基础优化方法，通过CLIPS定性推理得出最优桩长，从而简化优化数学模型中的约束条件；再运用二阶振荡粒子群算法在求解空间内定量搜索最优解，并以此方法为依据开发出一套桩基础优化设计系统，在兼顾计算精度和计算效率的前提下辅助用户实现桩基础优化设计．本文重点阐述优化设计方法及其程序设计，并通过工程算例分析说明此方法的合理性．

1 优化设计原理

1.1 知识推理基本原理

桩基础优化设计系统的知识推理模块是通过引入人工智能领域广泛应用的专家系统开发工具CLIPS实现的．

CLIPS是由美国国家航天局(NASA)约翰逊空间中心人工智能部在1985年用C语言开发的通用专家系统开发工具，属于典型的正向推理产生式系统，具有便于设计、表达方式灵活、运行效率高和兼容性好等优点[7]．CLIPS实现推理的基本构造如图1所示.

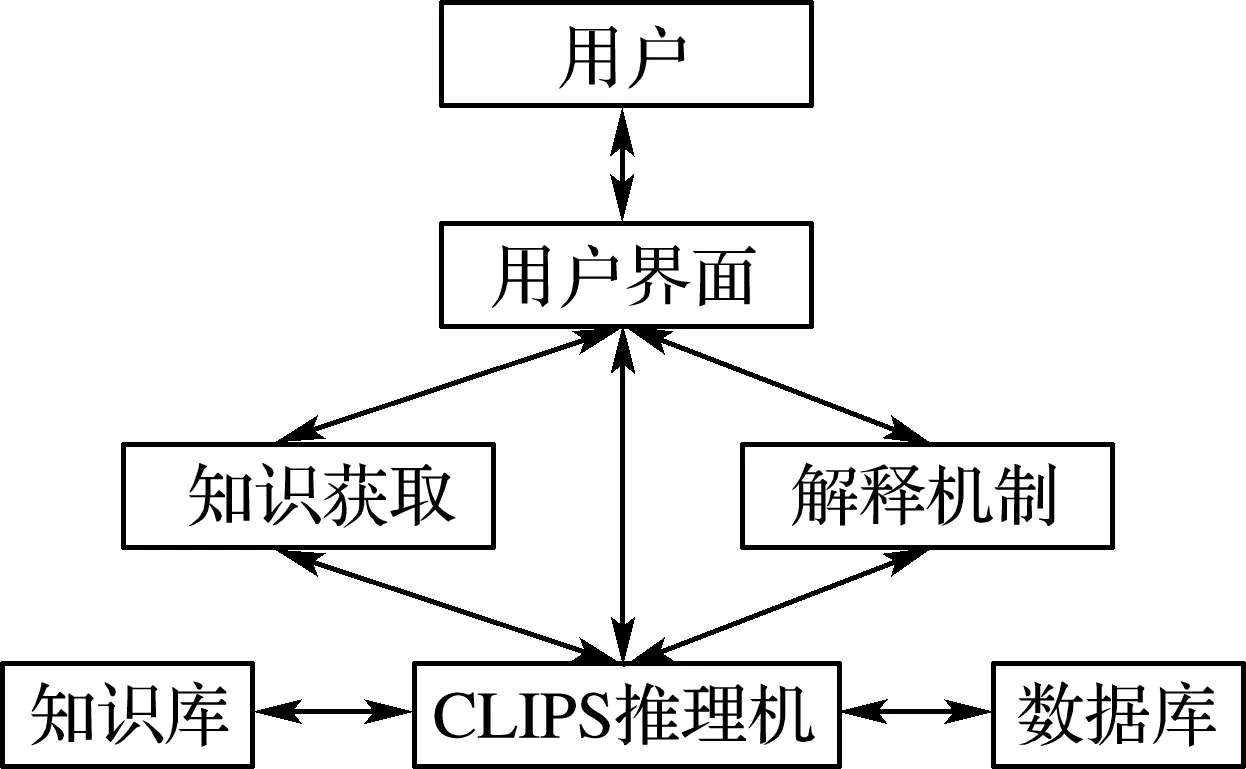
图1 推理实现的基本构造Fig.1 Basic structure of reasoning implementation

推理过程需要利用CLIPS在给定知识库下进行，知识库和推理机是CLIPS的核心．建筑桩基础规范内容和工程经验作为规则存储在知识库中，工程场地条件和上部结构设计参数等作为事实存储在数据库中，当事实与规则的前提条件相匹配时，则规则被激活；将所有被激活的规则按照既定优先级放入堆栈结构，再从堆栈顶部依次将规则取出，执行相应的动作，包括插入事实、删除事实和打印消息等，直到无已激活的规则或满足最大循环次数为止[8]．知识获取可以将处理后的事实反馈给知识库，实现知识库的更新．解释机制可以对求解思路进行追踪, 有助于系统的更新和维护．

CLIPS工具本身不具备用户图形界面开发能力，需要通过动态链接库的方式实现与C++语言或C#语言的接口调用[9-10]．本系统的知识推理模块采用C#语言内嵌CLIPS推理机实现，充分融合了CLIPS在知识推理方面开发效率高和C#语言便于设计、用户界面友好的特点．CLIPS还支持面向对象的编程风格，可与C#语言相互取长补短，将除推理以外的数值计算问题交给C#语言来实现．对于桩基础埋深确定中遇到的不确定性问题，通过引入确信度因子推理出具有最高确信度的备选情况[11]．

1.2 粒子群优化算法

粒子群优化算法(PSO)是受到鸟群捕食行为启发而提出的一种智能搜索算法，其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解，最早由Kennedy等[12]提出．

粒子群优化算法的求解思路是初始化一群位置和速度都随机的粒子，通过评价每个粒子的适应值找到个体最优位置和全局最优位置，粒子根据这两个最优位置来不断更新自己的速度和位置，追随当前最优粒子在解空间内搜索并反复迭代求解，迭代终止条件为达到预设的最大迭代次数或最小适应度阈值．

如果粒子在n维空间的位置表示为矢量Xi=(x1x2…xn)，飞行速度表示为矢量Vi=(v1v2…vn)，粒子i当前的位置和飞行速度分别为xi和vi，pbest i和gbest i分别为粒子i目前为止找到的最优位置和整个群体目前为止找到的最优位置，粒子i通过下面的公式来更新自己的速度和位置：

vi=ωvi+c1r1(pbest i-xi)+c2r2(gbest i-xi)

(1)

xi=xi+vi

(2)

式中：ω为惯性因子，取值范围在(0,1)，ω的取值可以对算法的全局搜索能力和局部搜索能力进行平衡调整；c1和c2是学习因子，能调整微粒自身经验与群体经验在其运动中所起作用的权重，通常取c1=c2=2；r1、r2是介于(0,1)的随机数；每个粒子都有一个最大限制速度vmax，如果超过vmax，那么速度就被限定为vmax，故粒子i的速度vi∈[-vmax,vmax]．

1.3 二阶振荡粒子群算法

标准粒子群优化算法主要依靠粒子间的合作，粒子本身没有变异机制，容易受制于局部极值约束陷入局部最优解，而无法得到全局最优解．

考虑到以上缺陷，国内外许多学者在标准粒子群优化算法的基础上提出了自己的改进方法，目的是加快收敛速度，以跳出局部最优解．比较典型的粒子群改进算法有Clerc提出的通过使用收敛因子控制粒子的飞行速度[13]；Shi等提出按照线性递减规律动态修改惯性因子的值[14]；文献[15]提出学习因子同步变化和异步变化的思想；Angeline将遗传算法的思想引入粒子群算法中，增加了变异机制[16]；文献[17]通过结合模糊规则实现收敛因子的动态自适应调整．本文考虑到优化数学模型经简化后目标函数复杂度较低，程序耗时较短，故选取了搜索精度较高的二阶振荡粒子群算法作为优化算法[18]．

二阶振荡粒子群算法的思想是将粒子速度的更新用粒子位置的改变来描述，并引入了振荡因子，粒子i的速度更新公式为

vi=ωvi+c1r1[pbest i-(1+ε1)xi(t)+(1+ε1)xi(t-1)]+c2r2[gbest i-(1+ε2)×xi(t)+(1+ε2)xi(t-1)]

(3)

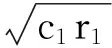
2 优化数学模型

2.1 目标函数

前人对于桩基础优化数学模型中目标函数的设计已有研究，主要有以下两种方案：一种是何水源等[19]提出的以承台混凝土用量最小作为目标函数，从桩的几何排布角度进行优化；另一种是李海峰等[20]、王成华等[5]提出的以桩基础总造价最小作为目标函数，在满足约束条件下通过总造价公式将可优化的设计参数联系到一起，通过求造价的最小值对设计参数进行优化．

本文采用第二种方案，假定桩基础造价与钢筋混凝土用量成正比，以承台和基桩总造价最小为目标函数进行优化．与其不同的是，桩长在桩基础设计阶段已通过知识推理模块设计成最优长度，故在优化过程中可视为常量，这样不但降低了桩基础总造价函数的复杂度，而且能够在选择合理持力层的前提下对桩长进行优化，更符合实际工况．

以桩基础总造价F为目标函数可表示为

F=F1+F2

(4)

式中：F1为承台造价，F2为基桩造价．

承台造价F1的表达式为

F1=C1abt+C2(Asaa+Asbb)ρs

(5)

式中：C1为承台单位体积混凝土综合单价，C2为承台单位质量钢筋综合单价；a、b、t分别为承台的长度、宽度、厚度；Asa和Asb分别为沿承台长和宽两个方向的配筋面积；ρs为钢筋的密度，一般取为7.8 t/m3．

基桩造价F2的表达式为

F2=∑C3Al+2C4Alρiρs/3

(6)

式中：C3为桩单位体积混凝土综合单价，C4为桩单位质量钢筋综合单价；A为桩身截面积；l为桩长；ρi为截面配筋率．

2.2 优化设计变量

由目标函数可知，在给定钢筋混凝土造价和配筋参数的前提下，桩长、桩径、桩数、承台长度、承台宽度和承台厚度都是影响桩基础总造价的重要因素，应选为优化设计变量．但桩长已通过CLIPS推理为最优桩长，故不再选为优化设计变量．桩间距的大小会影响到承台尺寸和桩基础最终沉降量，也应选为优化设计变量．

2.3 约束条件

桩基础优化设计需要满足三个方面的约束条件：强度约束、变形约束和构造约束．

强度约束包括单桩承载力约束、桩身强度约束、承台抗弯承载力约束、承台抗冲切承载力约束、承台抗剪切承载力约束和局部受压承载力约束，以上桩基础设计公式参见《建筑桩基技术规范》(JGJ 94—2008)．

变形约束主要指沉降约束：

S≤[S]

(7)

式中：S为桩基础最终沉降量；[S]为规范规定的沉降允许值．

构造约束条件限制桩径、桩长、桩间距和承台厚度，表达式如下：

dmin≤d≤dmax

(8)

H1≤l+z≤H2

(9)

3d≤s≤6d

(10)

t≥t0

(11)

式中：dmax和dmin分别为施工条件允许的最大和最小桩径，一般可取dmax=1 m，dmin=0.3 m；z为承台相对于天然地面的埋深；H1和H2分别为持力层顶面和底面的高度；s为桩间距；t为承台厚度，t0为某一下限值．

3 桩基础优化设计系统

3.1 系统组成结构

桩基础优化设计系统在辅助用户参照规范完成桩基础设计的基础上实现优化，系统由桩基础埋深推理、桩基础设计参数控制、桩基础设计模型控制和图形控制等模块组成，组成结构如图2所示.

图2 桩基础优化设计系统组成结构Fig.2 Composition structure of pile foundationnoptimum design system

系统通过桩基础设计参数控制模块获取建筑场地的工程地质条件、上部结构荷载和钢筋混凝土材料等参数，它为桩基础埋深推理模块与桩基础设计模型控制模块提供数据支持，由于涉及的数据量不大，选用Microsoft Office Access数据库．

桩基础埋深推理模块通过CLIPS对桩基础设计参数控制模块提供的数据进行推理分析，得出当前条件下最优土层作为桩端持力层，然后根据桩基础规范规定确定桩端嵌入持力层的最小深度，进而得出当前建筑场地条件下最优的基础埋深，最优桩长通过基础埋深减去承台埋深得到．

桩基础设计模型控制模块通过面向对象方法在类内部实现桩基础设计功能，包括单桩承载力计算、桩数初步估算、初选承台尺寸、单桩承载力验算、软弱下卧层验算、桩基础沉降计算、桩身结构强度验算和承台设计验算．如设计不满足规范要求，系统会提示用户修改相应设计参数重新计算，桩基础设计界面如图3所示.

图3 桩基础设计界面Fig.3 Pile foundation design interface

图形控制模块通过ObjectARX技术对CAD进行二次开发并建立图形库，为桩基础设计模型控制模块提供工程图例支持．

3.2 桩基础优化程序

作者基于知识推理和二阶振荡粒子群算法运用C#语言编制了桩基础优化程序，程序流程图如图4所示．优化程序可通过调用桩基础设计程序检验初始化粒子是否满足桩基础设计要求，如不满足要求，则重新初始化粒子．程序的随机数生成通过C#语言自带的Random类实现.

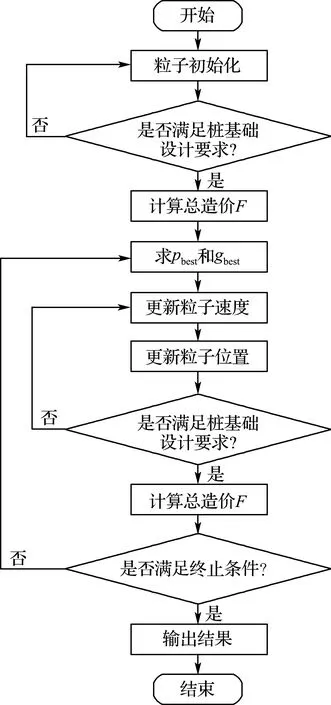
图4 桩基础优化程序流程图Fig.4 Flow chart of pile foundation optimum program

4 工程算例分析

某十层实验教学楼位于市中心区，上部结构为框架结构，主梁、次梁、楼板均为现浇整体式，混凝土强度等级为C30．建筑场地地势平坦，位于非地震地区．场地地下水为潜水，距离地表 2.1 m，根据已有资料，地下水对混凝土没有腐蚀性．各土层的分布情况及物理力学性质指标见表1．

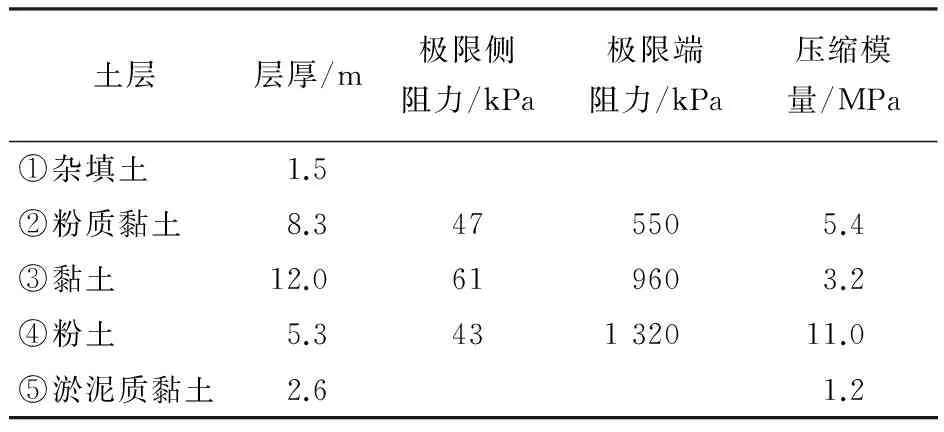
表1 各土层物理力学性质指标Tab.1 Physical and mechanical properties of soil layers

本工程选用预制桩基础，为避免对环境的噪声污染和对地层的扰动，采用静压法施工．系统的埋深推理模块通过分析各土层的参数，选择压缩性较低、承载力较高的第4层粉土层作为桩端持力层，然后系统会自动根据知识库中存储的《建筑桩基技术规范》对当前的粉土持力层工况进行匹配，最终确定桩端全断面进入持力层的最小深度为2d，其中d为桩径．为防止地下水对承台的影响，承台埋深设计为1.8 m．最终确定桩基础的最小埋深为20+2d．待设计阶段确定桩基础尺寸后可求出最优桩长．

下面以J6桩基础设计为例进行分析．框架柱截面尺寸300 mm×400 mm，传至桩基础的荷载效应标准组合为竖向力N=5 080.6 kN，x方向弯矩Mx=62.4 kN·m，y方向弯矩My=-13.4 kN·m，x方向水平力Qx=35.0 kN，y方向水平力Qy=4.6 kN．预制桩的桩径0.5 m，最优桩长最终确定为21 m．承台设计成6桩承台，两排，承台尺寸4 500 mm×2 500 mm，承台厚度1.1 m．混凝土强度等级为C25，钢筋采用HRB335型号．经单桩承载力验算、软弱下卧层验算、桩基础沉降计算、桩身结构强度验算和承台设计验算，均满足规范要求．

本文对J6桩基础进行优化，优化变量选择桩径、桩数、桩间距、承台长度、承台宽度和承台厚度，优化结果如表2所示．

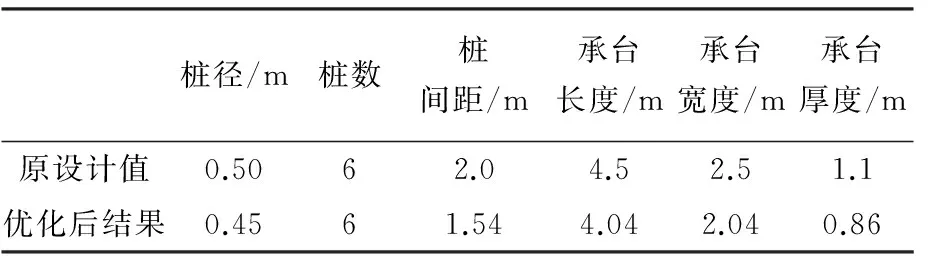
表2 J6桩基础优化计算结果Tab.2 Optimization calculation results of J6 pile foundation

由表2可知，相比于原设计方案，优化方案的桩径、桩间距、承台长度、承台宽度及承台厚度都有所减少．优化后的混凝土用量为27.13 m3，与原设计方案的37.12 m3相比节约了近27%．

5 结 论

(1)本系统通过C#语言内嵌CLIPS推理机的方式实现桩基础埋深推理功能，可以推理出最优桩长，从而简化优化数学模型中的优化变量．

(2)以承台和基桩总造价为目标函数，将各优化变量通过数学公式联系到一起，以规范要求的桩基础设计强度、地基变形和承台构造为依据建立约束条件．

(3)引入二阶振荡粒子群算法作为桩基础优化算法，结合优化数学模型和约束条件编制出桩基础优化程序，该算法能够避免陷入局部最优解，同时具有收敛速度快、搜索精度高的优点．

(4)通过一个十层实验教学楼案例对系统的设计优化功能进行测试分析，程序计算结果对于近一步研究桩基础优化问题具有一定的指导意义．

[1]阳吉宝,赵锡宏. 高层建筑桩箱(筏)基础的优化设计[J]. 计算力学学报, 1997, 14(2):241-244.

YANG Jibao, ZHAO Xihong. Optimum design for piled box (raft) foundation of tall building [J]. Chinese Journal of Computational Mechanics, 1997, 14(2):241-244. (in Chinese)

[2]阳吉宝,任 臻,周小刚. 带裙房的高层建筑基础的优化设计[J]. 土木工程学报, 1998, 31(5):39-47.

YANG Jibao, REN Zhen, ZHOU Xiaogang. Optimum design of foundations for high-rise buildings with podiums [J]. China Civil Engineering Journal, 1998, 31(5):39-47. (in Chinese)

[3]杨 敏,殷海涛. 人工神经网络确定和优化桩基持力层[J]. 同济大学学报(自然科学版), 2007, 35(2):156-160.

YANG Min, YIN Haitao. Defining and optimizing bearing stratum of piles with ANN [J]. Journal of Tongji University (Natural Science), 2007, 35(2):156-160. (in Chinese)

[4]蒋晓静. 多高层建筑上部结构和桩筏基础优化方法研究[D]. 上海:上海交通大学, 2007.

JIANG Xiaojing. Optimization research on superstructure of tall buildings and piled raft foundation [D]. Shanghai:Shanghai Jiao Tong University, 2007. (in Chinese)

[5]王成华,曾超峰,刘伟鹏. 基于混沌粒子群算法的桩基础优化设计方法[J]. 建筑结构, 2016, 46(2):76-81.

WANG Chenghua, ZENG Chaofeng, LIU Weipeng. Optimal design method for pile foundation based on chaotic particle swarm algorithm [J]. Building Structure, 2016, 46(2):76-81. (in Chinese)

[6]刘伟鹏. 竖向荷载作用下群桩的混沌粒子群优化设计方法研究[D]. 天津:天津大学, 2007.

LIU Weipeng. Researches of the chaotic particle swarm optimization design method for group piles under vertical loadings [D]. Tianjin:Tianjin University, 2007. (in Chinese)

[7]邓海平,何玉林,杜 静,等. CLIPS嵌入VC++技术的实现与应用[J]. 计算机工程与应用, 2005, 41(15):88-90, 132.

DENG Haiping, HE Yulin, DU Jing,etal. The realization and application of the technology embedding CLIPS within VC++ [J]. Computer Engineering and Applications, 2005, 41(15):88-90, 132. (in Chinese)

[8]吉奥克 J C,赖利 G D. 专家系统原理与编程[M]. 印 鉴,陈忆群,刘星成,译. 北京:机械工业出版社, 2006.

GIARRATANO J C, RILEY G D. Expert Systems Principles and Programming [M]. YIN Jian, CHEN Yiqun, LIU Xingcheng, trans. Beijing:Machinery Industry Press, 2006. (in Chinese)

[9]韦 辽. 在C#.NET中调用CLIPS的技术实现与应用[J]. 机械工程师, 2015(2):39-41.

WEI Liao. Implementation and application of calling the CLIPS technology in the C#.NET [J]. Mechanical Engineer, 2015(2):39-41. (in Chinese)

[10]周海清,王权明,陈正汉. 内嵌CLIPS推理引擎的中文专家系统开发工具及其在厦门市深基坑支护结构选型专家系统中的应用[J]. 岩石力学与工程学报, 2002, 21(z2):2558-2561.

ZHOU Haiqing, WANG Quanming, CHEN Zhenghan. Realization of a Chinese expert system developing tool with the CLIPS reasoning engine embedded [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(z2):2558-2561. (in Chinese)

[11]李正良,杨 光,晏致涛. 高层建筑基础设计智能决策支持系统研究[J]. 地下空间, 2004, 24(2):208-211, 219.

LI Zhengliang, YANG Guang, YAN Zhitao. Research on intelligent decision support system for design of high-rise buildings foundation scheme [J]. Underground Space, 2004, 24(2):208-211,219. (in Chinese)

[12]KENNEDY J, EBERHART R C. Particle swarm optimization [C] // Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway:IEEE Press, 1995.

[13]CLERC M. The swarm and the queen:towards a deterministic and adaptive particle swarm optimization [C] // Proceedings of the 1999 Congress on Evolutionary Computation-CEC99. Piscataway:IEEE, 1999.

[14]SHI Yuhui, EBERHART R C. Parameter selection in particle swarm optimization [J]. Lecture Notes in Computer Science, 1998, 1447:591-600.

[15]SHI Yuhui, EBERHART R C. Modified particle swarm optimizer [C] // Proceedings of the IEEE Conference on Evolutionary Computation, ICEC. Piscataway:IEEE, 1998:69-73.

[16]ANGELINE P J. Evolutionary optimization versus particle swarm optimization:philosophy and performance differences [C] // Proceedings of the 7th Annual Conference on Evolutionary Programming. Berlin:Springer-Verlag, 1998:601-610.

[17]SHI Yuhui, EBERHART R C. Fuzzy adaptive particle swarm optimization [C] // Proceedings of the 2001 Congress on Evolutionary Computation. Piscataway:IEEE, 2001:101-106.

[18]李武军,周 洲,许 放,等. 基于二阶振荡粒子群算法的高空长航时无人机翼型设计方法研究[C] // 2014(第五届)中国无人机大会论文集. 北京:航空工业出版社, 2014.

LI Wujun, ZHOU Zhou, XU Fang,etal. Research on high-altitude long-endurance UAV airfoil based on second order oscillating particle swarm optimization algorithm [C] // Proceedings of 2014 (the 5th) China UAV Congress. Beijing:Aviation Industry Press, 2014. (in Chinese)

[19]何水源,邓安福,王 成. 群桩基础优化设计及其在工业厂房中的应用[J]. 重庆建筑大学学报, 1999, 21(2):23-27.

HE Shuiyuan, DENG Anfu, WANG Cheng. Optimum design for pile group foundation and its application in factory building [J]. Journal of Chongqing Jianzhu University, 1999, 21(2):23-27. (in Chinese)

[20]李海峰,陈晓平. 高层建筑桩筏基础优化设计研究[J]. 岩土力学, 1998, 19(3):59-64.

LI Haifeng, CHEN Xiaoping. Research on optimizing design of pile raft foundation for high-rise building [J]. Rock and Soil Mechanics, 1998, 19(3):59-64. (in Chinese)

Pile foundation optimum design based on knowledge reasoning and second order oscillating particle swarm algorithm

YU Yazhou1,WANG Yin1,YANG Qing*1,CHEN Long2

(1.State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China；2.School of Civil Engineering, Dalian University of Technology, Dalian 116024, China )

In order to assist designers to complete pile foundation design work efficiently and reduce the construction cost, a pile foundation optimization design system based on knowledge reasoning and the second order oscillating particle swarm algorithm is developed. By combining C# language and CLIPS inference engine, the system can realize the reasoning function of pile foundation depth and find out the optimum pile length under current site condition. The objective function of optimum mathematical model is designed based on the construction cost, and the optimum variables are simplified according to the optimum pile length. The second order oscillating particle swarm algorithm is selected as the optimization algorithm, and the pile foundation optimization program is worked out according to the constraints of code for pile foundation design. Finally, a ten-storey experimental teaching building is chosen as an example to prove the feasibility of the optimization algorithm.

knowledge reasoning; the second order oscillating particle swarm algorithm; pile foundation optimum design; construction cost

1000-8608(2017)04-0383-07

2016-12-10；

2017-05-12．

国家自然科学基金资助项目(41572252)；国家自然科学基金青年基金资助项目(51409036).

于亚洲(1990-)，男，硕士，E-mail:yazhou_yu@163.com；杨 庆*(1964-)，男，博士，教授，博士生导师，E-mail:qyang@dlut.edu.cn.

TU473.12

A

10.7511/dllgxb201704008